深部咸水层CO2地质封存数值模拟参数的全局敏感性分析
——以苏北盆地盐城组为例
2014-07-05施小清吴吉春
郑 菲,施小清,吴吉春,赵 良,陈 旸
南京大学地球科学与工程学院,南京 210093
深部咸水层CO2地质封存数值模拟参数的全局敏感性分析
——以苏北盆地盐城组为例
郑 菲,施小清,吴吉春,赵 良,陈 旸
南京大学地球科学与工程学院,南京 210093
基于对苏北盆地盐城组下段砂岩储层概化建立二维径向剖面模型,运用TOUGH2/ECO2N程序模拟深部咸水层中CO2迁移分布过程。采用定性(Morris法)和定量(Sobol和EFAST法)全局敏感性分析方法,以储层中注入井处的压力、气相CO2总量及CO2气相羽扩散距离作为模型响应变量,对储层的水平渗透率、孔隙度、残余液体饱和度、孔隙分布指数、压缩系数、进气压力的倒数和盐度7个参数进行全局敏感性分析,讨论了咸水层的水文地质参数、盐度及其他模型参数对CO2封存运移泄漏过程的影响。Morris和Sobol法的敏感性分析结果都表明,对于不同的响应变量,参数的敏感性排序不同:以注入井处的压力为响应变量时,孔隙度的敏感性最高;以气相CO2总量和CO2羽扩散距离为响应变量时,水平渗透率的敏感性最高。EFAST 1阶及总敏感度分析结果与Sobol分析结果基本一致,但EFAST法相对Sobol法计算更高效稳健,需要的样本数较少。
CO2地质封存;全局敏感性分析;Morris法;Sobol法;EFAST法;苏北盆地
0 前言
随着社会经济的发展、人类活动的增加及化石能源的大量利用,大气中以CO2为主的温室气体的浓度持续增加,导致全球气候变暖和海洋酸化,对生态系统和人类的生存环境产生严重影响[1]。由于咸水层广泛分布于世界上的沉积盆地中且咸水不能作为饮用水源等原因,CO2深部咸水层封存被认为是目前减少CO2排放最具发展前景的方法之一。我国华北平原大部,四川盆地、准噶尔盆地东南部等许多盆地都是将来优先考虑的CO2封存场地,封存潜力巨大[2]。其中苏北盆地是近海陆相沉积盆地,面积约3.5×104km2,蕴含丰富的油气资源,具有咸水层封存CO2的巨大潜力。由于人类生产活动对岩层完整性的破坏,不密封的断层、天然裂缝等的存在[3-4],注入到咸水层的CO2将在浮力作用下通过渗漏通道向上部逃逸,导致CO2封存存在一定的泄漏风险。为确保注入的CO2能安全、有效、长久地封存在地下咸水层中,有必要对影响CO2泄露的因素进行敏感性分析,从而确定影响CO2封存泄露的主要因子。
目前国内外已有多位学者应用TOHGH2-ECO2N/TOUGHREACT[5-6]开展了深部咸水层CO2地质封存影响因素的研究。Zhou等[7]以Illinois盆地西蒙山含水层为例,建立了盆地尺度和CO2羽尺度下的整合模型,表明低渗透率和高进气压力具有二次密封效应,可阻滞CO2向上迁移,而注入井附近压力增量会促使储层中CO2-咸水向上运移进入上覆含水层;Brirkholzer等[8]选取盖层渗透率及压缩系数,进行了大尺度CO2封存区域压力增量的敏感性分析,表明这2个参数的变化对储层压力增量的影响均较大;Wiese等[9]开展了影响CO2单井注入速率的参数局部敏感性分析,表明渗透率的影响最大,注入压力的影响次之,垂向各向异性的影响较小;李义连等[10]分析了江汉盆地高盐度卤水对CO2封存过程中所发生的物理化学变化的影响,表明高盐度卤水层中单纯地注入CO2会造成注入井附近岩盐大量沉淀,不利于CO2安全储存及持续注入;柯怡兵等[11]开展了江汉盆地咸水层CO2封存注入数值模拟研究,对盐度的敏感性分析表明储层盐度越高压力积累越严重;赵锐锐等[12]进行了松辽盆地深部咸水层CO2注入的流体迁移模拟研究及参数敏感性分析,表明残余气体饱和度、注入层的各向异性数值对CO2溶解捕获的影响最大,盐度次之,残余液体饱和度和初始CO2浓度的影响最小。这些成果为研究咸水层CO2地质封存影响因素提供了定性认识,但已有研究往往仅局限于单个参数因素进行情景或局部敏感性分析。
全局敏感性分析方法目前主要包括Morris筛选法[13]、傅里叶幅度敏感度检验法(FAST/EFAST)[14-15]以及基于方差分析的Sobol法[16]等。近年来的研究成果[17-19]表明,全局敏感性分析可同时分析多个参数变化及参数间相互耦合作用对模型输出结果的直接和间接影响,较局部敏感性分析(只能分析单个参数对模型结果的直接影响)更接近实际,可全面地检测输入参数对模拟结果的影响,有助于模型使用者更好地理解识别模型结构和解释模拟结果。目前关于全局敏感性分析方法已广泛应用于地理空间分析模型[20]、气候模型[21]、水质模型[22]等模型敏感性分析中,但针对CO2地质封存模型进行全局敏感性分析的研究甚少。
笔者以苏北盆地盐城组下段砂层为研究对象,建立简单的二维径向模型,应用TOUGH2/ECO2N[5]模拟注入的CO2在地质储层中的溶解迁移以及CO2-咸水驱替过程,重点运用定性(Morris法)和定量(Sobol和EFAST法)全局敏感性分析方法针对不同的响应变量,对选取的模型参数进行全局敏感性分析,探讨和分析各参数的变化对深部咸水层CO2地质封存泄露的直接和间接影响。
1 CO2地质封存的数值模型
1.1 研究区地质概况
苏北盆地内部发育一系列北东向的南陡北缓的断陷和凹陷,是油气聚集的良好场所[23-24],也为CO2地质封存提供了良好的储存空间。盐城组是泛滥平原河流相沉积,以砂砾岩-中粗砂岩、细砂岩为主,属高孔隙高渗透性储集岩层。盐一段(下段)(Ny1)由3个沉积旋回组成,为粉砂质泥岩与中粗砂岩、细砾岩互层,顶部埋深一般在1 000.0 m以上,均厚300.0~400.0 m,含水层中的盐度约为1.5%,含水层孔隙度范围为12%~25%,渗透率范围为50.0~800.0 mD*mD为非法定计量单位, 1 mD=0.986 9×10-15 m2,下同。[25];盐二段(上段)(Ny2)中、上部是泥岩发育段,一般单层厚度为20.0~30.0 m,可作为有利的阻挡盖层[26]。该组地层基本符合CO2地质储存的选址条件,从储层埋深、岩层特征、区域盖层封堵性、地质圈闭条件等因素判断,可作为一个潜在的CO2地质封存场所。
1.2 概念模型建立

图1 一维CO2注入概念模型示意图(a)及网格剖分图(b)Fig.1 Schematic diagram for the 1D injection model (a) and the mesh (b)
笔者选取盐城组下段砂岩地层,建立二维径向模型,模拟CO2注入到均质各向异性咸水层中的运移演化过程(图1)。模型水平半径R为2.5 km,共划分为52个单元,网格间距随离井口距离增大而增大,最外侧单元设为无流量边界;垂直方向厚度H
为100.0 m,顶部及底部网格厚度均为2.0 m,设为无流量边界,其余网格厚度均为6.0 m,共18层。注入井半径设为0.5 m,CO2注入点位于距底部17.0 m处,恒定注入速率Qinj为0.1 kg/s,注入时间为10 a,总模拟时间为100 a。考虑到后续敏感性分析需要大量的计算时间,本文模拟范围较小但网格仍精细剖分,注入速率及模拟时间均设为较小值,以节省计算时耗同时避免影响到边界。盐城组下段砂层顶部埋深为1 000.0 m,模型顶部静水压强p约为10.0 MPa,能使注入的CO2以超临界状态存在。系统温度T为45 ℃,岩石颗粒密度、热传导率及比热分别为2 600 kg/m3、2.51 W/(m·℃)、920 J/(kg·℃)。相对渗透率及毛管压力的概化分别采用Van Genuchten-Mualem模型和Van Genuchten模型,输入参数详见表1[25]。
1.3 模拟结果分析
注入阶段,由于气相CO2(超临界状态,以下统称为气相)密度比水小,注入的CO2在浮力作用下向上迁移,孔隙中气相CO2饱和度逐渐增大,运移至盖层底部时由于受到阻挡,开始在盖层底部聚集并沿底部侧向扩散迁移(图2a);整个注入阶段,注入井的压力增量最大,10 a末注入井压力为1.06×107Pa(图2b);停止注入后,CO2继续向上并沿盖层底部侧向迁移(图2c),100 a后气相羽的迁移距离为335.4 m。CO2饱和度逐渐降低,最大饱和度由0.52减小为0.21,表明越来越多的CO2溶解在储层咸水中,储层压力增量得以缓慢释放。10 a后CO2
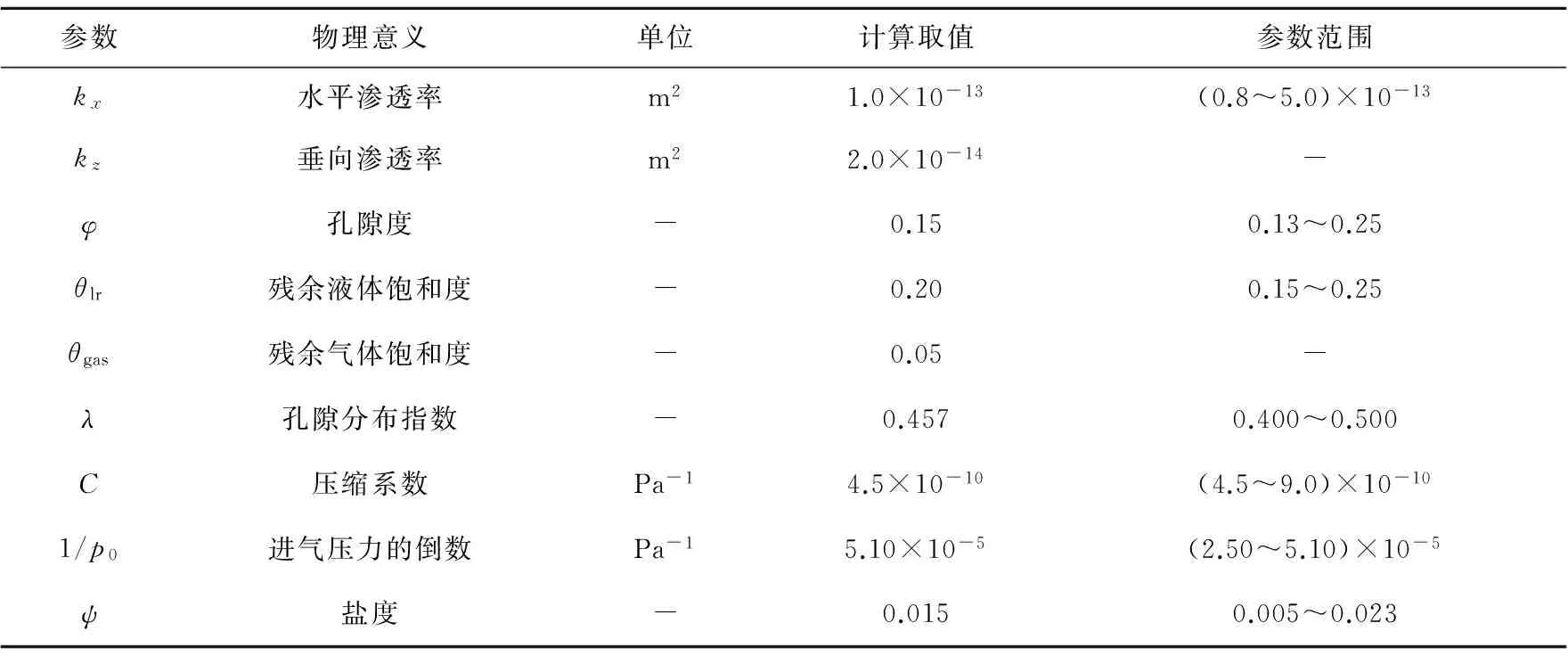
表1 模型中的水文地质及其他参数
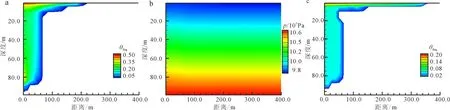
图中θliq为气相CO2饱和度。图2 10 a后气相CO2饱和度(a)、储层压力(b)以及100 a后气相CO2饱和度(c)的分布情况Fig.2 CO2 gas saturation (a),Spatial distribution of pressure (b) after 10 years and CO2 gas saturation after 100 years (c)
注入总量为3.2×107kg,气相及溶解相CO2各占总注入量的60%和40%;100 a后气相CO2溶解于咸水中使得溶解相CO2含量增加,各占总注入量的38%和62%。
CO2注入到储层后,由于压力积累可能诱发岩石破裂,破坏地层的密封性及完整性,导致储层中的气相CO2在浮力的作用下持续向上部逃逸,发生CO2泄露,其可能的泄漏范围与CO2驱替区域大小密切相关。为了评估模型参数对CO2封存泄漏的影响,笔者选取注入结束时(10 a后)注入井处的压力(此时储层压力增量最大)、气相CO2总量及模拟结束时(100 a后)CO2气相羽沿盖层底部的扩散距离作为下文敏感性分析的响应变量。
2 全局敏感性分析方法
2.1 Morris法
Morris法[13]是定性全局敏感性分析方法,用于识别和筛选较敏感的输入参数。假设模型有n个参数,参数的取样点数为q,每个参数都从对应的q个取样点上随机取值,获得向量X=[x1,x2,…,xn]。构造m×n(m=n+1)的矩阵,矩阵中相邻2行只有1个参数不同。取构造矩阵中相邻两行的组合参数作为模型参数值,输入模型计算相应的输出结果y1和y2,获得相应参数的敏感度|Δy|/Δ。其中:Δy为输出结果的变化量,Δ为输入参数的变化量。由于Morris法的随机性,很容易在一次随机取样及随机化过程中出现误差,所以需进行多次重复取样,获得单个参数敏感度的均值和方差。Morris[12]提出2个指标:1)均值,表征单个参数的敏感度,确定参数的敏感性排序;2)标准差,表征参数间相互作用的影响。该法的详细原理和计算步骤见文献[13,25]。
2.2 Sobol法
Sobol法的核心是把模型参数分解为单个参数及参数之间相互组合的函数[16],当参数正交时,模型具有唯一的分解形式。将模型总方差分解为单个参数单独作用的方差和多个参数同时作用的方差:
(1)
其中:D为模型总方差;Di为参数xi单独作用的方差;Di,j为参数xi和xj同时作用的方差;D1,2,…,n为n个参数同时作用的方差。
对上式归一化:
(2)
可计算模型单个参数或参数之间相互作用的一阶或高阶敏感度,即Si=Di/D,Si,j=Di,j/D。 方程(1)可改写为
(3)
其中:Si为1阶敏感度;Si,j为2阶敏感度;S1,2,…,n为n阶敏感度。第i个参数的总敏感度定义为STi=∑S(i),其中,S(i)为所有包含参数i的敏感度。
2.3 Extend FAST法

和
(4)
其中,Z0为非零整数。

该方法中参数的取样数为
(5)

3 敏感性分析结果与讨论
对第2节中已建立的数学模型采用Morris、Sobol及EFAST法探讨各参数及参数间相互作用对模型输出结果的影响。选取水平渗透率、孔隙度、残余液体饱和度、孔隙分布指数、压缩系数、进气压力的倒数和盐度7个参数,各参数不确定性取值范围见表1。
3.1 Morris分析结果
采用Morris法对7个参数重复抽样10次获得80组样本,各响应变量的敏感性分析结果如图3所示。
图3a为以注入井处的压力为响应变量的分析结果。由图3a可见:孔隙度的敏感性最高,其与其他参数相互作用对模型输出的影响也最为显著;其次为压缩系数和水平渗透率。无论是从均值还是标准差的角度来看,孔隙分布指数和盐度的敏感性均较小。孔隙度及压缩系数影响CO2存储空间,水平渗透率影响CO2的迁移速率,从宏观上直接影响储层中积累压力的传递释放,参数取值较大,可有效地减小储层压力积累。

图3 以注入井处的压力(a)、气相CO2总量(b)及CO2气相羽的扩散距离(c)为响应变量的Morris敏感性分析结果Fig.3 Sensitivity analysis results of Morris based on the injection well pressure (a), the total mass of gas-phase CO2 (b) and the spread distance of CO2 gas plume (c) as response variables
图3b为以气相CO2总量为响应变量的分析结果。由图3b可见:水平渗透率的敏感性最大,其次为孔隙度和进气压力的倒数,这3个参数与其他参数相互作用对模型输出的影响也最显著;压缩系数的敏感性最小。水平渗透率影响迁移速率,孔隙度影响储存空间,进气压力表征毛管阻力,CO2横向运移范围越大,毛管阻力越小,孔隙可存储的气相CO2总量越多。
图3c为以CO2气相羽的扩散距离为响应变量的分析结果。其中:水平渗透率的敏感性最高;其次为孔隙度和进气压力的倒数。渗透率与其他参数相互作用的影响最大,残余液体饱和度与其他参数相互作用的影响次之。水平渗透率越大,CO2羽沿盖层底部的横向迁移速率及扩散距离越大;气相CO2充满空隙后会继续向前运移,因此孔隙度越大,意味着驱替咸水后形成的CO2储存空间越大,则CO2羽的扩散范围越小;进气压力与毛管压力有关,毛管压力越大,CO2运移受到的阻力越大,迁移距离越小。
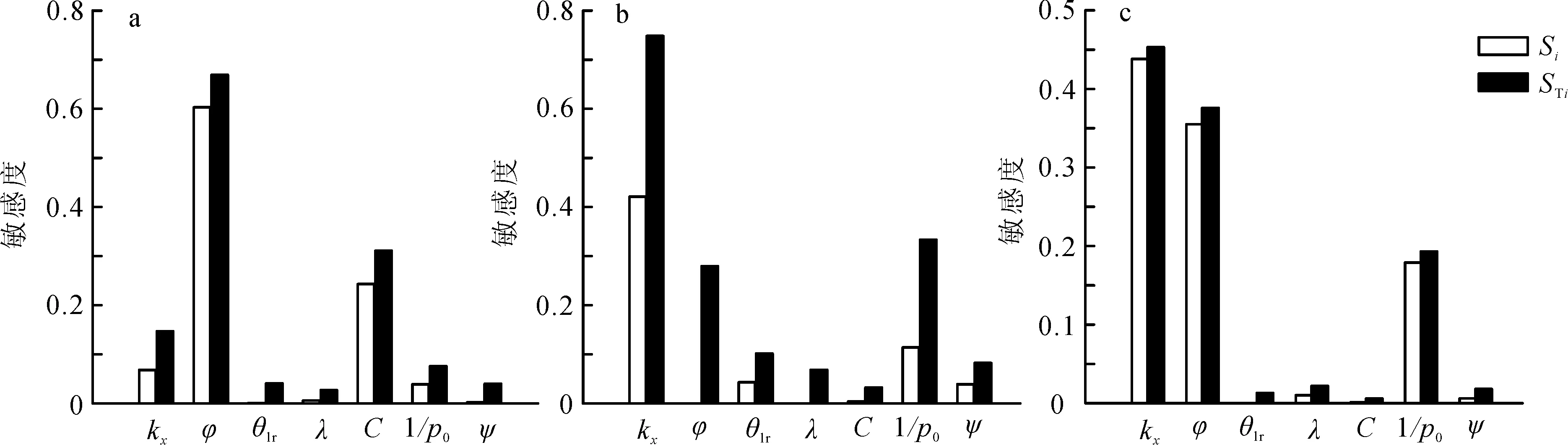
图4 以注入井压力(a)、气相CO2总量(b)及CO2气相羽扩散距离(c)为响应变量的Sobol 1阶敏感度及总敏感度分析结果Fig.4 First and total order sensitivity indices of Sobol based on the injection well pressure (a), the total mass of gas-phase CO2 (b) and the spread distance of CO2 gas plume (c) as response variables
总体而言,对于不同的响应变量,水平渗透率与孔隙度对模型输出的影响较大。考虑到Morris法不能定量说明参数间相互作用的不确定贡献率,为此进一步采用Sobol和EFAST法进行参数的定量敏感性分析。
3.2 Sobol法分析结果
由于Sobol法中取样数较少时,敏感度指数易受数值计算影响出现负值,所以本文经过多次取样计算测试稳定性后,选取取样个数为8 192。Sobol法的定量全局敏感性分析结果如图4所示。对于不同的响应变量,敏感参数的1阶敏感性排序结果(图4)与Morris分析结果(图3)相近,参数间相互作用的影响程度有所不同。对比参数的1阶敏感度及总敏感度可以看出,单个参数对模型输出的影响贡献是主要的,参数间相互作用对模型输出也具有一定的影响,但计算结果显示交互敏感度数值不大(以气相CO2总量为响应变量除外),因此本文未进行2阶敏感度分析。
Sobol的定量分析结果进一步表明,对于不同的响应变量,参数的敏感性排序不同,说明参数敏感性也具有不确定性。敏感性分析结果揭示了各参数在CO2封存过程中的控制影响作用不同。如图4a所示:以注入井处的压力为响应变量时,φ为最敏感参数,C为次敏感参数,其控制气相CO2存储空间,存储空间大则不易产生压力增量。图4b中,以气相CO2总量为响应变量时,kx为最敏感参数,1/p0为次敏感参数。1/p0影响毛管压力进而影响气相CO2总量,但kx表现为正影响,而1/p0表现为负影响。需要指出的是,此时φ的1阶敏感性较小,交互敏感性较大,与前述Morris的定性分析结果(图3b)中φ排序第二差异显著。这可能是因为Morris取样较少导致个别参数的敏感性分析存在误差,特别是当该参数的交互敏感度较大时,数值计算的微小误差使得Morris对孔隙度的分析结果产生了较大的偏差,而Sobol计算取样次数较Morris多,结果更为可靠。图4c中,以CO2气相羽的扩散距离为响应变量时,kx仍为最敏感参数,各参数间的交互敏感度较小,kx控制气相CO2的迁移速率,迁移速率越大,CO2羽横向扩散范围越大。综上所述,对于不同的响应变量,各参数对决定CO2封存运移的主要因素的影响程度不同,在模型中的影响效果的表现也不同,如kx,对于注入井处的压力表现为正影响,对于CO2羽扩散距离表现为负影响,易引发泄漏。对比分析Morris与Sobol的分析结果表明,当模型参数较多、参数间的关联性较小、相互作用较弱时,可先采用Morris筛选分析识别模型潜在的重要参数,以有效地减少参数维数降低计算时耗。
3.3 EFAST法分析结果
为了与Sobol法比较,依据EFAST法中参数的取样算法(式(5)),设置取样个数分别为2 023、3 031、4 039、5 047及7 007等,经计算测试后发现EFAST法在取样较少(3 031个)时计算结果即趋于稳定。以注入井处的压力和CO2气相羽扩散距离为响应变量的EFAST和Sobol的敏感度计算结果如表2所示(限于篇幅,其他结果未列出),对于不同的响应变量,EFAST计算所得出的各参数的主要敏感度及总敏感度分析结果与Sobol分析结果基本一致,由于多个参数(至少2个)的敏感度值在同一数量级上,数值误差的影响较小,使得EFAST和Sobol的计算结果相近。Sobol和EFAST均定量给出了各参数的主要敏感度和总敏感度值,它们的差值即为参数的交互敏感度,即参数间相互耦合作用的间接影响,实质上反映了模型“异参同效”的现象[18]。从表2中可见,当以注入井处的压力或以CO2气相羽扩散距离为响应变量时,参数的交互敏感度不大,说明参数的独立性较强,参数间的相关性较弱,表现为“异参同效”性较小。
值得一提的是,从敏感度计算结果(表2)上来看,尽管Sobol和EFAST 2种方法的分析结果基本一致,但是EFAST较Sobol的取样数要少得多,相应的计算过程中前者较后者要节省大量的计算时耗。以Windows XP系统、Intel core2 E7400 CPU、主频2.8 GHz、内存2 GB为例,运行1次正问题需耗时2.0~3.5 min。本次研究中,对于以注入井压力及CO2气相羽扩散距离为响应变量时,EFAST法较Sobol法计算分别节省时间约160.0和250.0 h。综上所述,EFAST法需要的样本数较少且计算高效、稳健,对于多参数模型,可较大程度地降低计算时耗,因此建议当模型参数较多时,可首选EFAST法进行定量全局敏感性分析。
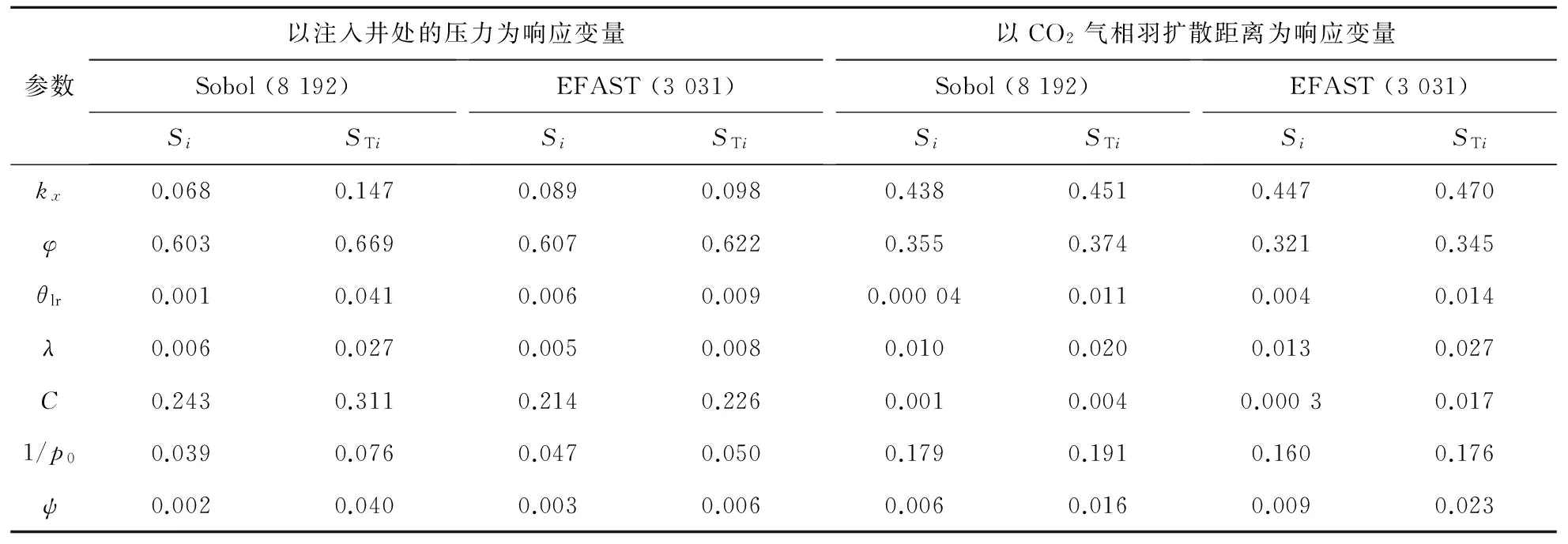
表2 EFAST与Sobol敏感性分析结果比较
4 结论与展望
1)基于对苏北盆地盐城组下段砂岩储层概化的数值模拟研究表明,CO2注入储层后会产生压力增量,气相CO2在浮力作用下向上运移沿盖层底部横向扩散迁移。本文选择储层注入井处的压力、气相CO2总量及CO2气相羽的扩散距离3个响应变量进行定性和定量全局敏感性分析,筛选评估影响CO2封存和运移的决定因子。
2)Morris定性全局敏感性分析可有效筛选识别模型重要参数。Morris和Sobol全局敏感性分析结果都表明,对于不同的响应变量,参数的敏感性排序不同,说明各参数对决定CO2封存过程主要因素的影响程度不同:以最大压力为响应变量时,孔隙度最敏感,其次为压缩系数和水平渗透率;以气相CO2总量为响应变量时,水平渗透率最敏感;以CO2气相羽的扩散距离为响应变量时,水平渗透率最敏感,其次为孔隙度。参数的交互敏感度,实质上体现了模型“异参同效”的现象,参数的交互敏感度小,表征参数的“异参同效”性较小。对于本例,以气相CO2总量为响应变量时,由于孔隙度的交互敏感度较高,取样次数较少的Morris敏感性排序产生了较大的偏差,而Sobol计算取样次数较多,结果更为可靠。因此对于Morris定性全局敏感性分析时需增加取样次数以避免交互敏感度较高参数的影响。
3)与Morris法相比,Sobol和EFAST全局敏感性分析方法可进一步定量参数不确定性影响的贡献率。EFAST需要的样本数较少且计算高效、稳健,建议当模型参数较多时,可首选EFAST法进行定量全局敏感性分析。但需要说明的是,无论Sobol还是EFAST法都无法充分利用样本的所有信息且计算量较大,对于多参数的模型评价计算费时。笔者拟下一步采用替代模型技术评价CO2封存过程中参数的敏感性以提高计算效率。
[1] Holloway S. Storage of Fossil Fuel-Derived Carbon Dioxide Beneath the Surface of the Earth[J/OL]. Annu Rev Energy Environ, 2001, 26:145-166,doi: 10.1146/annurev.energy.26.1.145.
[2] 李晓春, 刘延锋, 白冰, 等. 中国深部咸水含水层CO2储存优先区选择[J]. 岩石力学与工程学报, 2006, 25(5): 963-968. Li Xiaochun, Liu Yanfeng, Bai Bing, et al. Ranking and Screening of CO2Saline Aquifer Storage Zones in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(5): 963-968.
[3] 张旭辉, 鲁晓兵, 刘庆杰. 盖层特性对CO2埋存逃逸速度的影响[J]. 土工基础, 2009, 23(3): 67-70. Zhang Xuhui, Lu Xiaobing, Liu Qingjie. The Effect of the Characteristics of Cap on the Escaping Velocity of CO2[J]. Soil Eng and Foundation, 2009, 23(3): 67-70.
[4] 郭建强, 张森琦, 刁玉杰, 等. 深部咸水层CO2地质储存工程场地选址技术方法[J]. 吉林大学学报: 地球科学版, 2011, 41(4): 1084-1090. Guo Jianqiang, Zhang Senqi, Diao Yujie, et al. Site Selection Method of CO2Geological Storage in Deep Saline Aquifers[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(4): 1084-1090.
[5] Pruess K.ECO2N:A TOUGH2 Fluid Property Mo-dule for Mixtures of Water, NaCl and CO2[R]. Berkeley: Lawrence Berkeley Laboratory,2005.
[6] Xu T F, Sonnenthal E, Nicolas S, et al. TOUGHREACT User’s Guide: A Simulation Program for Non-Isothermal Multiphase Reactive Geochemical Transport in Variably Saturated Geologic Media[R]. Berkeley: Lawrence Berkeley Laboratory,2008.
[7] Zhou Q L,Birkholzer J T,Mehnert E,et al.Modeling Basin and Plume-Scale Processes of CO2Storage for Full-Scale Deployment[J]. Groundwater, 2010, 48(4): 494-514.
[8] Birkholzer J T, Zhou Q, Cortis A, et al. A Sensitivity Study on Regional Pressure Buildup from Large-Scale CO2Storage Projects[C]//Gale J, Hendriks C, Turkenberg W, et al. Energy Procedia:Vol 4. Ne-therlands: Elsevier Ltd, 2011:4371-4378.
[9] Wiese B, Nimtz M, Klatt M, et al. Sensitivities of Injection Rates for Single Well CO2Injection into Saline Aquifers[J]. Chemie der Erde, 2010, 70(53): 165-172.
[10] 李义连, 房琦, 柯怡兵, 等. 高盐度卤水对CO2地质封存的影响: 以江汉盆地潜江凹陷为例[J]. 地球科学: 中国地质大学学报, 2012, 37(2): 283-288. Li Yilian, Fang Qi, Ke Yibing, et al. Effect of High Salinity on CO2Geological Storage: A Case Study of Qianjiang Depression in Jianghan Basin[J]. Earth Science: Journal of China University of Geosciences, 2012, 37(2): 283-288.
[11] 柯怡兵, 李义连, 张炜, 等. 岩盐沉淀对咸水层二氧化碳地质封存注入过程的影响研究: 以江汉盆地为例[J]. 地质科技情报, 2012, 31(3): 109-115. Ke Yibing, Li Yilian, Zhang Wei, et al. Impact of Halite Precipitation on CO2Injection into Saline Aquifers: A Case Study of Jianghan Basin[J]. Geological Science and Technology Information, 2012, 31(3): 109-115.
[12] 赵锐锐, 孟庆辉, 成建梅. 深部咸含水层CO2注入的流体迁移模拟研究: 以松辽盆地三肇凹陷为例[J]. 岩土力学, 2012, 33(4): 1247-1252. Zhao Ruirui, Meng Qinghui, Cheng Jianmei. Fluid Migration Modeling of CO2Injection in Deep Saline Aquifers: A Case Study of the Sanzhao Depression, Songliao Basin[J]. Rock and Soil Mechanics, 2012, 33(4): 1247-1252.
[13] Morris M D. Factorial Sampling Plans for Preliminary Computational Experiments[J]. Technometrics, 1991, 33(2):161-174.
[14] Saltelli A, Anderes T H. Sensitivity Analysis of Model Output: An Investigation of New Techniques[J]. Comput Statist Data Anal, 1993, 15(2): 211-238.
[15] Saltelli A, Tarantola S, Chan K P S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output[J]. Technometrics, 1999, 41(1): 39-56.
[16] Sobol I M.Sensitivity Estimates for Nonlinear Mathematical Model[J]. Mathematical Modeling and Computational Experiment, 1993, 1: 407-414.
[17] 宋晓猛, 孔凡哲, 占车生, 等. 基于统计理论方法的水文模型参数敏感性分析[J]. 水科学进展, 2012, 23(4): 503-510. Song Xiaomeng, Kong Fanzhe, Zhan Chesheng, et al. Sensitivity Analysis of Hydrological Model Parameters Using a Statistical Theory Approach[J]. Advances in Water Science, 2012, 23(4): 503-510.
[18] 任启伟, 陈洋波, 舒晓娟. 基于Extend FAST方法的新安江模型参数全局敏感性分析[J]. 中山大学学报: 自然科学版, 2010, 49(3): 127-134. Ren Qiwei, Chen Yangbo, Shu Xiaojuan. Global Sensitivity Analysis of Xin’anjiang Model Parameters Based on Extend FAST Method[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(3): 127-134.
[19] 任启伟, 陈洋波, 周浩澜, 等. 基于Sobol法的TOPMODEL模型参数全局敏感性分析[J]. 人民长江, 2010, 41(19): 91-107. Ren Qiwei, Chen Yangbo, Zhou Haolan, et al. Global Sensitivity Analysis of TOPMODEL Model Parameters Based on Sobol Method[J].Yangtze River, 2010, 41(19): 91-107.
[20] Crosetto M, Tarantola S. Uncertainty and Sensitivity Analysis: Tools for GIS-Based Model Implementation[J]. International Journal of Geographical Information Science, 2001, 15(5): 415-437.
[21] Meszaros R, Zsely I G, Szinyei D, et al. Sensitivity Analysis of an Ozone Deposition Model[J]. Atmospheric Environment, 2009, 43(3): 663-672.
[22] Pastres R, Chan K, Solidoro C, et al. Global Sensitivity Analysis of a Shallow Water 3-D Eutrophication Model[J]. Computer Physics Communications, 1999, 117(1): 62-74.
[23] 吕炳全, 王耀庭, 冯国清. 苏北溱潼高邮拉分盆地的基本特征和油气富集规律[J]. 西南石油学院学报, 1989, 11(2): 17-22. Lü Bingquan, Wang Yaoting, Feng Guoqing. Basic Characteristics of Qintong and Gaoyou Pull-Apart Basins in North Jiangsu and Their Laws of Oil and Gas Accumulation[J]. Journal of Southwestern Petroleum Institute, 1989, 11(2): 17-22.
[24] 朱静昌, 张国栋, 王益友. 苏北盆地阜宁群时期的古气候和水介质的物理化学条件分析[J]. 岩相古地理, 1992, 12(6): 8-16. Zhu Jingchang, Zhang Guodong, Wang Yiyou. Palaeoclimatic Conditions and Physicochemical Pro-perties of Water Bodies in the North Jiangsu Basin During the Funing Grounp Deposition[J]. Sedimentary Facies and Palaeogeography, 1992, 12(6): 8-16.
[25] 郑菲, 施小清, 吴吉春, 等. 苏北盆地盐城组咸水层CO2地质封存泄漏风险的全局敏感性分析[J]. 高校地质学报, 2012, 18(2): 232-238. Zheng Fei, Shi Xiaoqing, Wu Jichun, et al. Global Sensitivity Analysis of Leakage Risk for CO2Geolo-gical Sequestration in the Saline Aquifer of Yancheng Formation in Subei Basin[J]. Geological Journal of China Universities, 2012, 18(2): 232-238.
[26] 朱厚勤, 朱煜, 郑开富. 苏北盆地盐城组天然气藏成藏控制因素探讨[J]. 海洋地质动态, 2003, 19(9): 22-26. Zhu Houqin, Zhu Yu, Zheng Kaifu. Pooling Conditions and Controlling Factors of Gas Pools in Yancheng Formation of Subei Basin[J]. Marine Geology Letters, 2003, 19(9): 22-26.
Global Parametric Sensitivity Analysis of Numerical Simulation for CO2Geological Sequestration in Saline Aquifers:A Case Study of Yancheng Formation in Subei Basin
Zheng Fei, Shi Xiaoqing, Wu Jichun, Zhao Liang, Chen Yang
SchoolofEarthSciencesandEngineering,NanjingUniversity,Nanjing210093,China
TOUGH2/ECO2N code was used to simulate the complex coupled processes taking place during and after CO2injection in the deep saline sandstone aquifer of Lower Yancheng Formation in Subei basin. Morris, Sobol and EFAST methods were used to analyze the global sensitivity of parameters, i.e.,kx,n,Slr,λ,C, 1/p0andS, on three response variables: 1)the pressure located in the injection well; 2)the amount of gas-phase CO2and 3)the spread distance of CO2gas plume. Results from the Morris and Sobol methods show thatnis the most sensitive parameter for the injection well pressure,kxis the most sensitive parameter both for the amount of gas-phase CO2and the spread distance of CO2gas plume. In summary, the sensitivity orders of these parameters are totally different for different corresponding variables. Comparative results from EFAST and Sobol show that the main and total effect obtained from the two quantitative sensitivity analysis methods are basically identical, however, EFAST is computationally more efficient than Sobol in numerical experiment.
CO2geological sequestration; global sensitivity analysis; Morris; Sobol; EFAST;Subei basin
10.13278/j.cnki.jjuese.201401209.
2013-05-04
国家自然科学基金项目(41172206);江苏省自然科学基金项目(BK2012313);江苏省产学研联合创新资金计划项目(BY2010136)
郑菲(1987-),女,博士研究生,主要从事多相流数值模拟方面的研究,E-mail:xiaomi2008happy@163.com
施小清(1979-),男,副教授,博士,主要从事反应溶质运移模拟研究,E-mail:shixq@nju.edu.cn。
10.13278/j.cnki.jjuese.201401209
P641
A
郑菲,施小清,吴吉春,等.深部咸水层CO2地质封存数值模拟参数的全局敏感性分析:以苏北盆地盐城组为例.吉林大学学报:地球科学版,2014,44(1):310-318.
Zheng Fei,Shi Xiaoqing,Wu Jichun,et al.Global Parametric Sensitivity Analysis of Numerical Simulation for CO2Geological Sequestration in Saline Aquifers: A Case Study of Yancheng Formation in Subei Basin.Journal of Jilin University:Earth Science Edition,2014,44(1):310-318.doi:10.13278/j.cnki.jjuese.201401209.
