模糊聚类在节水灌溉方案优选中的应用

刘 森，于雪峰

(1.黑龙江省水利水电勘测设计研究院，哈尔滨 150080;2.黑龙江大学水利电力学院，哈尔滨 150080)

0 引言

我国幅员辽阔，土地面积广袤，做好节水灌溉方案优选不仅对于节约工程投资有着重要意义，并且对于节约水资源，发挥水资源的最大效益，有着举足轻重的作用。

节水灌溉一般主要从工程节水、方案优选等方面进行考虑来确定方案的优劣。

其中工程节水措施主要包括渠道防渗技术、低压管道输水灌溉、喷灌技术、微灌技术、地下渗灌技术、地面节水灌溉等[1]。

方案优选因素包括自然因素、技术因素、经济因素、社会因素、管理运行因素、农业因素和生态环境因素等。

方案优选从经济、管理、运行等多方面对节水灌溉问题进行具体分析，从而制定具体的解决方案，在节水灌溉的方案中起着决定性作用[2]。

目前用于节水灌溉方案优选的方法很多，比如文献中的TOPSIS模型、灰色关联投影法、模糊综合评判、集对分析法等，以上这些方法在节水灌溉优选中各有优缺点[3]。

以上方法有的主要分析各种因素在灌溉方案优选中的权重，也有的主要分析模型在方案优选中的重要作用[4]。

本文主要针对模型来说明模糊聚类在节水灌溉方案优选中的重要作用。

1 模糊聚类模型

1.1 模糊聚类模型简介

设有待聚类的n个样本组成集合

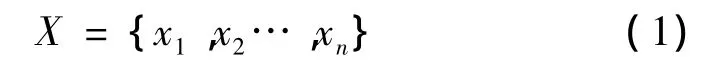
每个样本用m个指标特征值向量表示

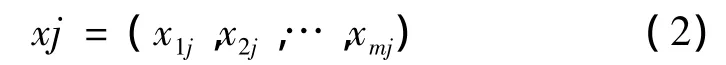
则可用m，x，n阶指标特征值矩阵:

对样本集进行聚类。

式中:Xij为聚类样本j指标i的特征向量，i=1，2，…，m;j=1，2，…，n 。

由于m个指标特征值物理量的量纲不同，在进行聚类时要先消除指标特征值物理量量纲的影响，使指标特征值规范化，规格化数在闭区间[0，1]范围内[5－6]。

采用何种类型的规格化公式，可根据实际问题而定、矩阵X经规格化后变为指标特征值规格化矩阵

式中:rij为指标特征值规范化数。

设将n个样本依据样本的m个指标特征值，按c个类别(级别)进行聚类[7－8]，其模糊聚类矩阵为:

式中:uhj为样本j归属于类别h的相对隶属度，h=1，2，…c。

满足条件:

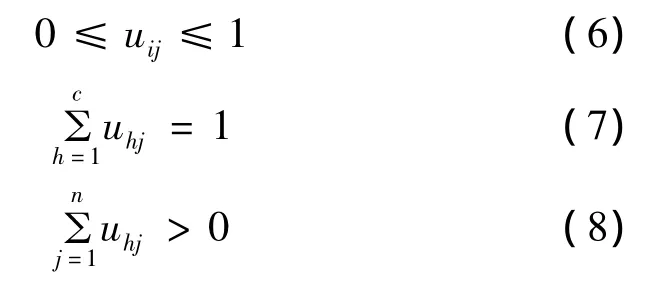
设类别h的m个指标特征值称为该类的聚类中心，则c个类别的指标特征值可用m，X，c阶模糊聚类中心矩阵:

来表示。

式中:sih为类别h指标i的特征值规范化数，0≤Sih≤1。

聚类样本j的m个指标特征值用向量表示为:

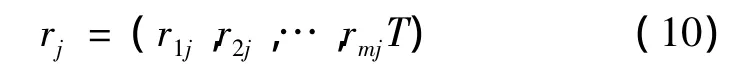
指标h的m个特征值即h类的聚类中心向量表示为:

在模糊聚类中考虑不同指标对聚类的作用不同，设指标全向量为:

已知矩阵S求解矩阵U:

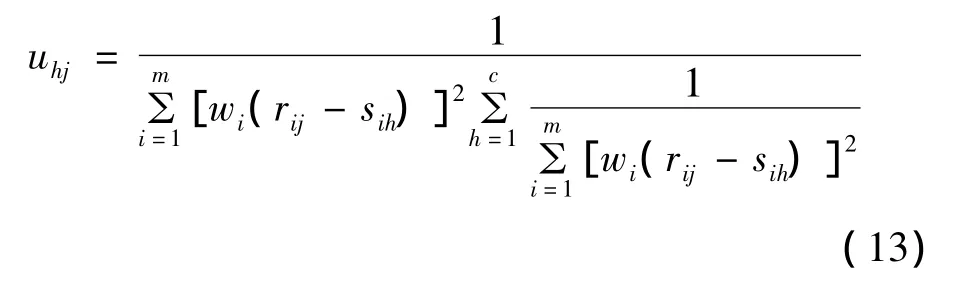
利用求出的U求解s矩阵:

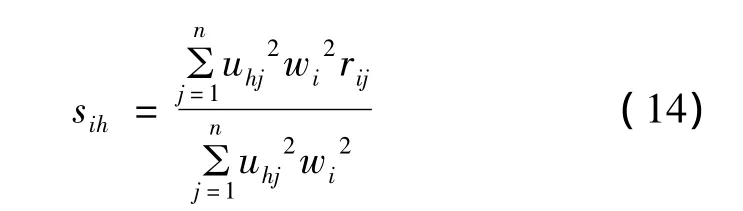
1.2 求解步骤

求解步骤共有4点:

1)给定uhj与sih所要求满足的精度ε1与ε2。

2)假设一个满足约束条件式7、8、9，矩阵元素不全相等的初始模糊聚类矩阵

2 应用实例

L某节水灌溉工程有管道工程、喷灌、滴灌、小管出流灌溉4个建设方案(分别为A、B、C、D)供选择，各方案评价指标见表1。

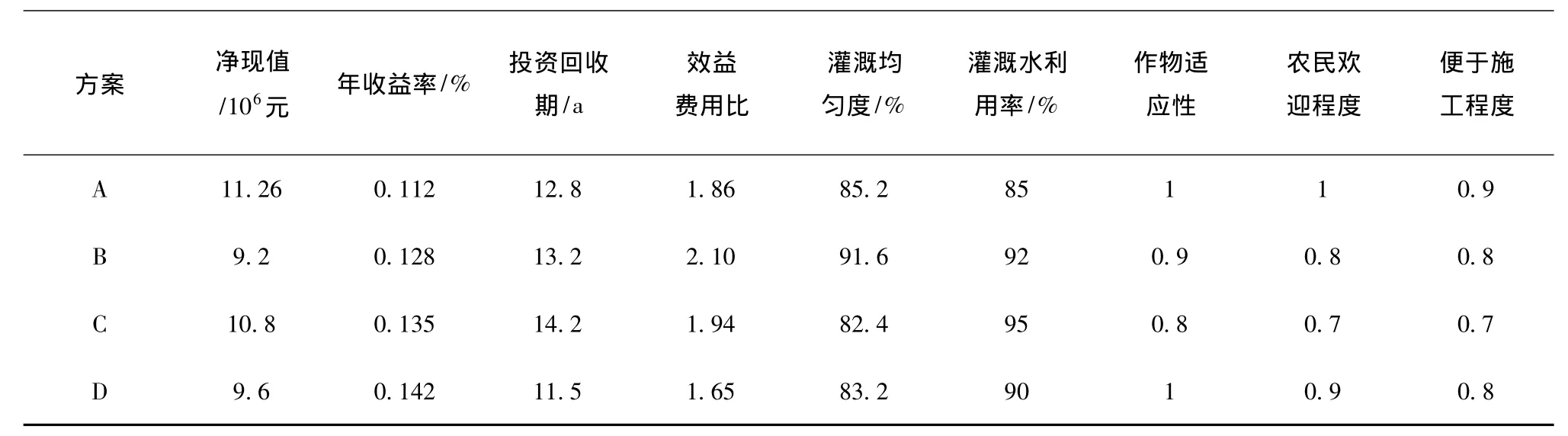
表1 各方案评价指标值

计算步骤如下:

1)利用式4将指标进行规范化:

由于本文主要针对模糊聚类模型进行分析，权重采用文献[2]权重进行计算。

2)权重矩阵:

W=[0.1219 0.11 0.1071 0.1081 0.1094 0.1089 0.1191 0.1134 0.1021]

3)计算级别c采用2级进行计算。

4)评价结果见表2。

表2 评价结果

由表2可知，方案A对于优的隶属度最大为最优方案，其次为方案D，再次为方案B，最后为方案C。这与文献[2]的评价结果完全一致。

3 结论

结论共有2点:

1)本文所用的模糊聚类方法的评价结果可信度较高，对于节水灌溉方案选择可以提出准确的依据。

2)本文4个方案对于优的隶属度差别较大，方案排序一目了然，便于读者接受。

[1]李洁，高新波，焦李成.基于特征加权的模糊聚类新算法[J].电子学报，2006(01):91－94.

[2]郭法强，杨昕馨，姚鹏亮.TOPSIS模型的节水灌溉方案优选[J].水利与建筑工程学报，2009，07(03):84－86.

[3]门宝辉.选择节水灌溉方式的灰色关联投影法[J].沈阳农业大学学报，2004(Z1):109－112.

[4]庄恒扬，沈新平，陆建飞.模糊聚类计算方法的理论分析[J].江苏农学院学报，1998(03):37 －41.

[5]高军省.节水灌溉方案优选的集对分析方法[J].2010(12):85－87.

[6]陈守煜.工程模糊集理论与应用[M].北京:大连理工大学出版社，2009:49－51.

[7]马军，邵陆.模糊聚类计算的最佳算法[J].软件学报，2001(04):106－109.

[8]王秀珍.模糊聚类分析法及其应用[J].长沙大学学报，1999(04):46－49.

[9]陈守煜，韩晓军，王建明.模糊聚类、识别、优选统一理论与循环迭代模型[J].大连理工大学学报，2004，44(06):883－886.

[10]邓辉，孙增圻，孙富春.控制理论与应用[J].2001，18(02):171－175.