探究高中文科生垂直证明的困难情况
——基于范希尔理论
2014-07-05杨文萍
杨文萍
目前关于文科生数学学习困难方面的研究,从所收集的文献资料来看,多数集中在从智力因素到非智力因素全面的说明学生基础差的原因,并且在实施差生转化策略时也没有针对某一知识点或者某一方面。尽管这些研究富有启发性,但范围实属宽泛。本研究为了更加具有针对性,且基于学生在立体几何学习方面表现出不佳的情况来看,本研究内容锁定为学生学习垂直所遇到的困难。因此,决定选择广州市某普通中学的高二一个文科普通班中的12个学生作为研究对象,本文确定研究内容为:(1)用范希尔的几何思维水平来评价学生的立体几何垂直证明的思维水平;(2)根据学生的思维水平发现学生学习立体几何垂直证明存在的困难。本研究方法主要是以内容分析法为主,分析对象主要是学生平时的作业以及测验卷。
1 理论基础
有关范希尔几何思维水平的介绍很多,本文采用鲍建生介绍的“范希尔几何思维分为视觉、分析、非形式化的演绎、形式化的演绎、严密性五个层次”[1]。下面将对这五个层次进行介绍。
(1)层次0:视觉(visuality)
对于图形,学生不仅能够简单的对图形进行操作,比如整体辨认、绘画或仿画,而且还能对图形进行描述,不管使用标准的还是不标准的名称。但是这种操作无法深入达到分析图形的状态,也无法概括论述图形。
(2)层次1:分析(analysis)
学生能对图形进行进一步的操作,即分析图形的基本结构及其特征从而解决基本的几何问题。虽然可以通过分析来区分两个图形,并进行分类,但是对图形性质间的关系比较模糊,也不知如何使用公式,更不会导出公式。
学生可以清晰地解释图形及其性质之间的关系,会使用公式,达到演绎的状态。但在陌生前提的条件下,无法使用定理证明结果,没有定理间的网络知识结构。
(4)层次3:形式化的演绎(formal deduction)
学生在达到前面三种水平的基础上,可以对几何证明进行演绎的推理,能猜测并能证明。能理解证明中的必要和充分条件。
(5)层次4:严密性(rigior)
在这个层次,能在不同的公里体系下严密地建立定理,以分析比较不同的几何体系,如欧氏几何和非欧式几何系统的比较。
由于范希尔理论是用0~4编号,本研究为了叙述的方便,在描述时会按照水平1~5的方式,编码为L1-L5。本文采用的是范希尔的五个层次的分类。
2 内容分析的设计与实施
内容分析是教育中的一种重要的研究方法,用它可对有关研究文献、实验记录、访谈记录、观察记录、教材、课堂讲授、学生作业等各种材料进行分析。“探讨心理与教育活动的规律”[2]。
第六,开磷拥有生态环保竞争优势。国家通过环保政策和市场化去产能,像开磷这样拥有规模实力、先进生产工艺和环保治理能力的大型企业将在结构调整中占据有利地位。
根据内容分析这种研究方法,本文将从以下五个方面来进行本研究的具体实施过程的阐述:
研究目的的确定。本研究是属于现状分析,基于研究者所执教的学生在考试时立体几何得分率很低,学生对于立体几何的学习叫苦连天。另外考虑到学生在做平行问题时完成得不错,而在垂直证明的问题上就表现出极大的阻力。再者高考中立体几何垂直问题占据一定位置,综合这几个因素确定本研究的目的是找出高二文科生的立体几何垂直证明问题的困难,并因此分析原因所在。
(2)分析单位。根据本文的研究目的是找出高二文科生的立体几何垂直证明问题的困难,并因此分析原因所在,因此本研究的分析单位就是文科生的有关立体几何垂直证明所做过的题目(这里包括作业和测验卷),即已经抽取了的研究材料。
(3)分析维度。根据3.3节范希尔几何思维的5个水平,将本文的分析维度划分为五个维度:层次0(视觉),编码为L1;层次1(分析),编码为L2;层次2(非形式化的演绎),编码为L3;层次3(形式化的演绎),编码为L4;层次4(严密性),编码为L5。把没做题目的和只从条件题目得出一个结论的这两种情况都视为层次0。其余的根据所写的情况分类。
(4)分析材料。根据研究材料的确定,从来源抽样,分析单位抽样,日期抽样三者结合在一起构成了本研究的研究材料。第1题是关于线线垂直的证明,此题需要通过作辅助线才能解决证明问题。第2题是关于线线垂直的证明,所考查的是勾股定理的逆定理以及线面垂直判定定理的运用。第3题是关于线面垂直的证明,其中涉及的知识点有勾股定理的逆定理和面面垂直的性质定理。第4题是2009—2010年广州市期末教学质量检测考试的一道立体几何考试题目,本题是节选垂直的证明。第5题是2008—2009年广州市期末教学质量检测考试的一道立体几何考试题目,本题是节选垂直的证明。“据已有的数学教学任务水平分类可以把数学任务的认知要求化分为3种类型或层次:记忆、理解、探究”[3],所选的五道题都属于理解层次。
(5)评判记录。在此对这12人在按照成绩高低顺序后,用英文大写字母X~I进行编码,题目编号就是1~5。字母和数字放在一起就表示某个人完成的某道题,如X1表示的就是第一个人完成的第一道题,A5表示第四个人完成的第五道题。为了能够明显看到学生几何思维处于哪种水平,从而看到学生学习几何垂直证明的学习情况,特制定以下表格1。表格的每一行表示某学生的每道题的思维水平,比如第二行表示学生X的思维水平,相对应的每个空格表示每道题的思维水平情况。

表1 被试垂直证明思维水平层次
3 研究结果
根据学生的作业和卷子的完成情况,运用范希尔的几何思维五种层次,研究者在表1中记录学生的立体几何中垂直证明的思维层次,显示结果如表2所示。

表2 被试垂直证明思维水平层次显示
不考虑题目的题号,不考虑学生的人数,表2中总共有60个层次结果。根据统计计算,大多数集中在第2层次,其次是第1层次,接着是第4层次、第3层次,最后才是第5层次。具体数据为:L2共计29个,L1共计14个,L3共计8个,L4共计9个,L5共计0个。按照总数为60个来计算百分比,第1层次占据23.3%,第2层次占据48.3%,第3层次占据13.3%,第4层次占据15%,第5层次占据0。具体如表3所示。
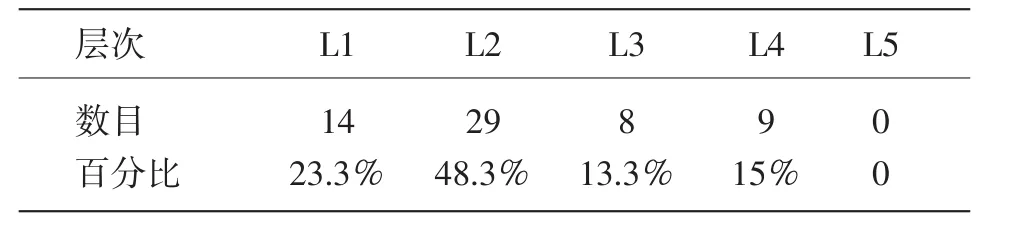
表3 各思维层次的数目及其百分比
由表3可以知道没有一位学生达到范希尔的几何思维第5层次,所以以下分析仅仅从范希尔的第1至第4层次思维分析学生的作业和卷子的完成情况。
(1)第1层次
在表3中我们可以看到L1出现的次数为14次,学生的垂直证明思维归属于此层次,主要是由于学生因为没有作答或者只写出了一句话。没有作答并不仅仅是因为不知道如何完成该题目,而是在做卷子时,由于时间限制未能在限定的时间解决出来以至于题目的空白。另外有位学生是因为平时没有完成作业的习惯,而导致所需做的题目空白。
(2)第2层次
在表3中我们可以看到L2出现的次数为29次,但是学生并没有出现29种出错的情况,他们所犯错误都有相同之处,归纳起来就是:①性质定理的误用。一见到面面垂直,就直接想到线面垂直;或者一见到面面垂直,就直接得出线线垂直,并没有考虑面面垂直的性质是什么。另外,两个平面的交线在垂直的情况下会变得很特殊,即在两个平面垂直的条件下,交线就会垂直于任一平面的所有直线。而对于矩形,就直接认为矩形的对角线是互相垂直的。②知识的负迁移。学生在初中的数学学习当中已经接触过平行线,其传递性的性质即“三条直线中,只要有两条直线平行于第三条直线,则它们也相互平行”对学生的影响极大。学生们认为在垂直中也有同样的性质,于是他们得出“若两条直线垂直于同一直线,那么这两条直线也互相垂直”的错误结果。③知觉无恒常性。由于缺乏立体感,看到立体的图形都用平面的直觉来表示,认为看到的图形就是真实的。④方法选取的不恰当。比如,用全等三角形的方法来证明两条直线垂直,不懂得怎样作辅助线。⑤概念的误解。比如,认为直三棱柱的侧面是互相垂直。⑥目标不明确。在证明线面垂直时,得到的结果是面内的直线垂直另外一个新的平面。
(3)第3层次
在表3中我们可以看到L3出现的次数为8次,学生所犯错误可以归结于两种情形:①理所当然型。此类型表现在学生答题思路虽然正确,但是在证明的过程中,有一步的某一条件需要证明的没有给出证明,或者理所当然认为是条件已经给出的,或学生自己假设,而这一步其实是可以从已知条件中推出的。②戛然而止型。在证明的过程中,前面进行得很顺利,但是在接近快要完成证明的时候突然停止没再继续往下证明,有时候就差一步就可以完成。
(4)第4层次
在表3中我们可以看到L4出现的次数为9次,相对于前面的三个层次来说,此层次的水平要高,它表现在学生可以正确的完成题目,包括语言组织和思路的整理。
4 研究结论
本研究通过用范希尔的几何思维水平理论来分析学生在学习立体几何垂直证明中的思维水平,进而分析学生在学习立体几何垂直证明中存在的困难。经过前面的分析,可以得出以下结论:
(1)学生在证明立体几何垂直问题方面表现出了兴趣的缺乏。与学生相对没那么抗拒的平行证明来说,立体几何垂直证明问题牵涉的知识点要多。涉及的关系越多、知识点越多,需要学生所掌握的知识就越多。由此学生在证明时遇到了困难,表现出了极大的挫败感,因为知识的掌握不多,再加上挫败感,让学生几乎丧失对此的学习。
(2)学生在学习三维的知识时会受到二维知识的影响,在学习新知识时会有负迁移的情况。其一,学生在学习面面垂直的性质时表现出了极大的困难。这种困难就表现在学生没有弄清在什么情况下才能从面面垂直得出线面垂直,看到“面面垂直”这个刺激物,就直接得出的反射结果“线面垂直”或者“线线垂直”。或者从另外一个角度来分析就是学生对于从面到线的变化有着迷惑,追溯到从线到面会有什么样的性质变化也是学生的困惑点。基于这样的困惑点,学生在做题的时候就表现得一览无余。其二,学生在学习垂直时往往会受到平行的一些性质的影响。比如,由“同时平行于同一直线的两直线平行”,学生可以得出“同时垂直于同一直线的两直线垂直”。
(3)学生学习立体几何垂直证明受到知觉无恒常性的影响。由于知觉无恒常性,导致缺乏立体感,看到立体的图形都用平面的直觉来表示,认为看到的图形就是真实的,从而就有立体几何图形怎么看都不立体,怎么看都是平面。
(4)学生做立体几何垂直证明题时不擅长用分析法。分析法不擅长表现在学生在证明时,目标不明确,不明白自己所要证明的结论和题目或者是自己写的东西有什么联系。
[1] 鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:4-5.
[2] 董奇.心理与教育研究方法[M].北京:北京师范大学出版社,2004:304.
[3] 姚静.数学任务框架:一种教学反思的理论[J].贵州师范大学学报(自然科学版),2003(3):31-35.
