粒度分布对胶结砂岩力学特性的影响
2014-07-05刘先珊
刘先珊,许 明
(1.重庆大学土木工程学院,重庆 400045;2.重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400045)
粒度分布对胶结砂岩力学特性的影响
刘先珊1,2,许 明1,2
(1.重庆大学土木工程学院,重庆 400045;2.重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400045)
储层出砂过程中砂岩颗粒的离散与其细观结构性有密切关系。以胶结砂岩为研究对象,基于三维颗粒流数值模型(PFC3D)建立4种不同粒度分布的数值模型,模拟剪切过程的砂岩力学响应,研究不同粒度分布的砂岩体应力比、体应变、配位数和黏结破坏与轴应变之间的关系。结果表明:粒度分布对砂岩力学特性的影响较大,仅基于随机方法产生颗粒建立的数值模型不能完全代表实际砂岩的物理结构。须根据实测的砂岩粒度分布建立三维数值模型,才能准确描述储层砂岩的力学特性。粒径越小,连接的颗粒越少,自由度越大,开采中成为离散颗粒的可能性越大。
细观结构;胶结砂岩;粒度分布;三维颗粒流数值模型;力学特性
储层砂岩是由砂粒胶结而成的沉积岩,不仅外界赋存环境对其力学特性影响大,且砂岩的细观结构,如砂岩颗粒的排列、大小、胶结性等都起着重要的控制作用。目前,一些学者[1-3]从细观力学角度分析了黏性土的结构性,并研究了结构性对其力学特性的影响。但砂岩与土体介质的结构有本质区别,蒋明镜等[4-5]基于室内试验分析了不同颗粒级配对火山灰岩力学特性的影响。但室内试验分析介质的细观结构对岩石力学特性的影响由于试验工作量大、周期长、数据离散性大等问题,不能准确描述颗粒性态与力学响应的非线性关系。对于颗粒间含有胶结物质的储层砂岩,胶结性对力学特性的影响较大[6],尹小涛、唐娴等[7-8]采用颗粒流数值模型研究颗粒尺寸效应对岩体力学特性的影响,但主要基于点接触模型,只能模拟颗粒的转动和点接触力的传递。储层砂岩的胶结物质不仅限制了砂岩颗粒的转动,还对承力起着重要作用,因此为了更准确地模拟胶结砂岩的力学特性,具有一定接触面积的平行黏结模型[6,9-12]能限制颗粒转动,并能传递力和力矩,可以更好地反映砂岩颗粒的受力性能。笔者以储层砂岩为研究对象,基于实测的砂岩颗粒分布建立三维颗粒流数值模型(PFC3D),分析外力作用下砂岩的力学响应,与试验结果进行对比,验证该数值模型的可行性。
1 不同粒度的胶结砂岩力学试验
胶结砂岩由于颗粒间胶结物质的存在,外荷载作用下的力学响应不同于一般的松散砂岩,胶结物质对其力学性质起着重要作用,而胶结物质附着于颗粒之间,不同粒径的颗粒连接有较大的差异。选取3个圆柱形试验模型,模型高度为0.08 m,直径为0.04 m,试验砂岩的颗粒与颗粒充分黏结在一起,形成孔隙-接触的胶结类型,胶结物为碳酸盐的混合物[13]。试验模型的颗粒组成累积分布曲线如图1所示,砂岩颗粒特征及详细分布如表1、2所示。可以看出,试验模型1为由实际储层砂岩配置而成的砂岩模型,颗粒粒径均匀,级配不良,试验模型2的级配好且连续,试验模型3的颗粒分布范围较大,但颗粒的分布不连续,小颗粒的含量较大,未压实时的孔隙大。
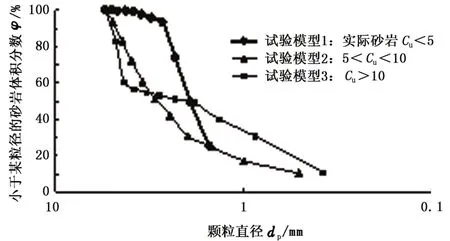
图1 试验模型的颗粒组成累积分布曲线Fig.1 Cumulative distribution curves of particle for testing model
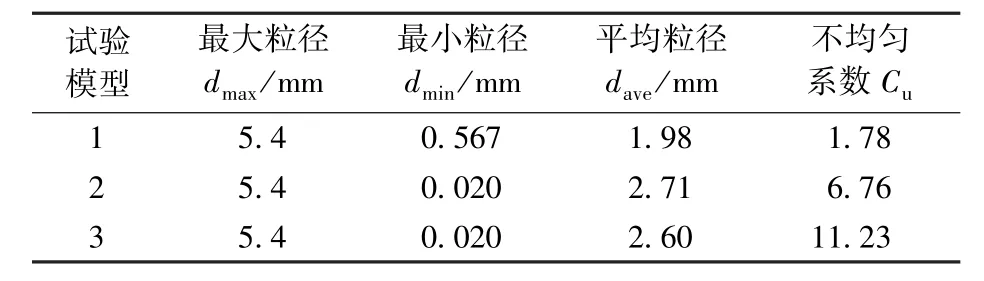
表1 试验砂岩的颗粒特征Table 1 Particle characteristics of testing sandstone
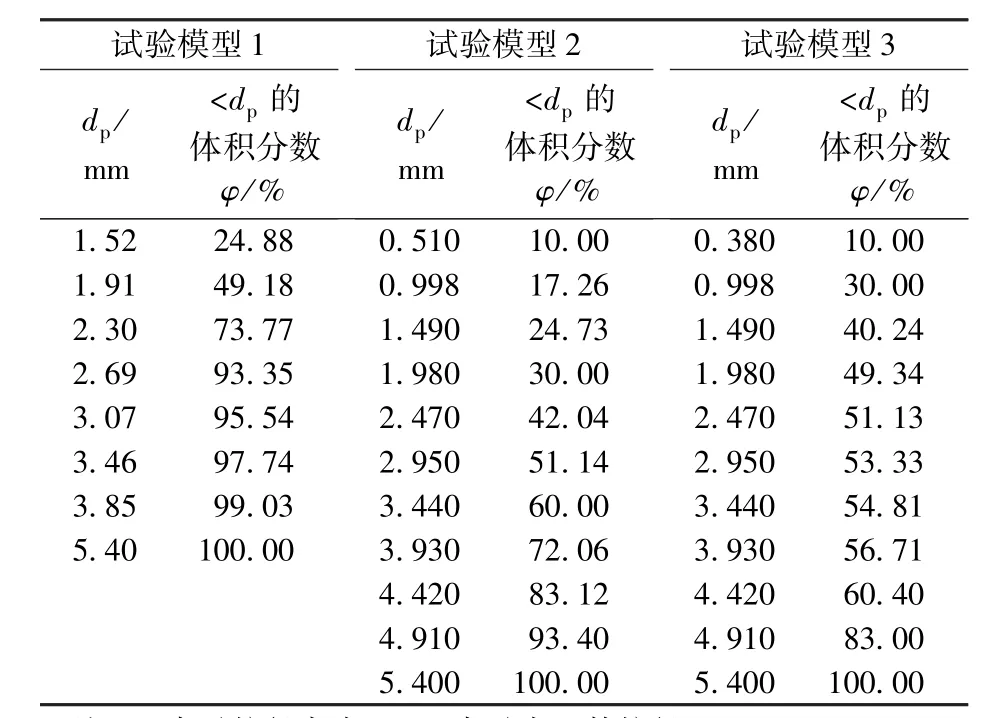
表2 试验砂岩的颗粒分布Table 2 Particle size distribution for testing sandstone
在三轴仪上进行剪切试验,顶板加载速度为0.02 mm/s,底板静止,3个砂岩试样的力学响应如图2的应力比与轴向应变关系及体应变与轴向应变关系。图2(a)显示试验模型2得到的峰值应力比值最大,主要是该试样的不均匀系数5<Cu=6.76<10,砂岩的粒度分布曲线较平缓,级配良好,砂岩压密性较好,当胶结物质存在于颗粒间时,颗粒间的咬合作用较强,随着轴向应变增大至2.5%,应力比值上升较快,达到峰值应力比值后,下降的速度相对较快,脆性更强一些。试验模型1对应实际储层砂岩,不均匀系数Cu=1.78<5,粒径范围较窄,颗粒级配不良,且粒径为1~3 mm的颗粒约占70%,颗粒间均匀胶结,中值粒径为1.98 mm,相对于其他试验模型得到较小的应力比值。试验模型3的不均匀系数Cu=11.23>10,粒径分布范围较大,图1所示粒径小于1.0 mm的颗粒约占30%,粒径大于4 mm的颗粒约占40%,粒径较大和较小的比例较重,未压实时的模型孔隙率较大,剪切过程中小颗粒更容易进入到大的孔隙中,因此峰值应力比值最小,且达到峰值应力比值对应的应变会较大。
图2(b)所示的εV~εa关系与图2(a)的变化趋势一致,由于试验模型2级配良好,试验过程中剪缩较小,但剪胀效应较明显;试验模型3为不连续级配试验,则在试验过程中,剪缩较大,剪胀效应并不明显,与图2(a)变化曲线一致;试验模型1的剪缩和剪胀效应居于两者之间。上述结果说明级配良好的胶结砂岩试样在剪切过程中能得到较大的峰值应力,剪缩与剪胀效应相对较温和,而对于级配不良的试样,试验过程中较小颗粒上的胶结物质更容易剥离,失去胶结物质的小颗粒进入大的孔隙中,随着应变的增大,峰值应力较小,剪缩较大。
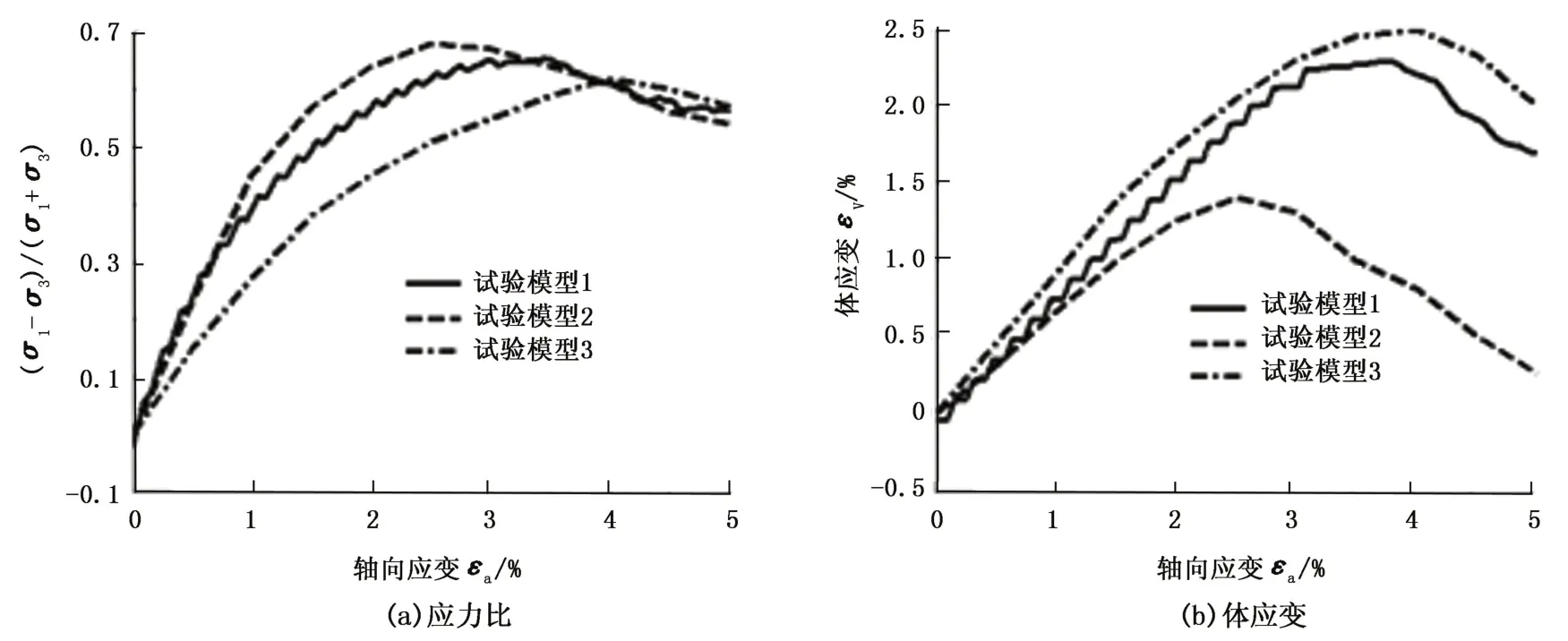
图2 应力比及体应变变化曲线对比Fig.2 Comparison of variation curve of stress ratio and volume strain using different methods
2 数值模型及颗粒连接性分析
从细观角度考虑不同粒度分布对砂岩力学特性的影响,建立4种粒度分布的数值模型[6],模型高度为0.08 m,直径为0.04 m。4种颗粒分布的主要参数如表3所示。力学计算参数为:颗粒密度2 650 kg/m3,颗粒摩擦系数0.25,颗粒法向刚度、切向刚度均为6.286×103kN/m,平行黏结法向刚度、切向刚度均为8.27×108kPa/m,平行黏结法向强度、切向强度均为5.2×104kPa。粒度分布曲线如图3所示。数值计算中,对初始的砂岩颗粒流模型逐渐加载,一旦围压达到10 MPa,基于PFC3D的Fish语言进行二次开发[6],模拟具有一定面积、刚度和胶结量的砂岩体以模拟砂岩的胶结性状,本文中考虑砂岩颗粒为全胶结。开始模型剪切试验,设置模型顶板加载速度为0.02 mm/s,底板静止。

表3 计算工况Table 3 Calculation cases
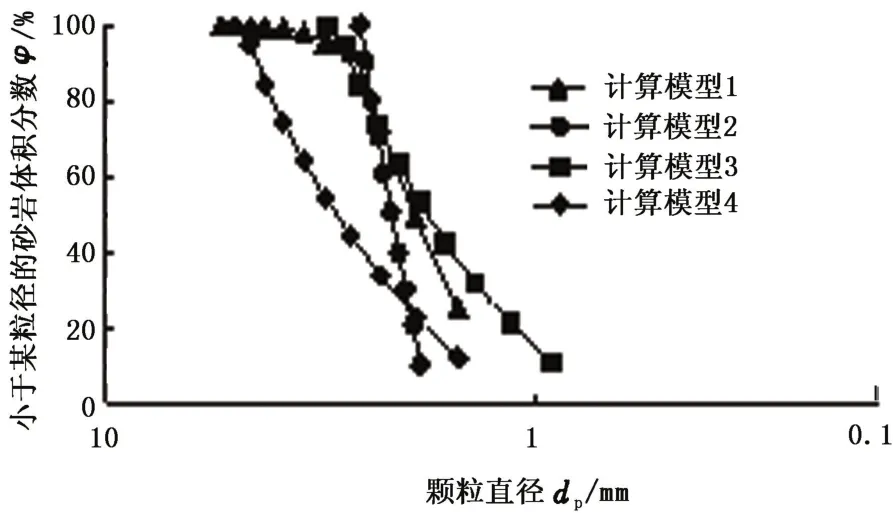
图3 颗粒组成累积分布曲线Fig.3 Cumulative distribution curves of particle size
为了验证该数值模型的可行性,将计算模型1 (实际颗粒分布)的数值计算结果与试验结果进行比较。数值计算中,砂岩试样确定,砂岩颗粒密度和胶结物质相同。首先模拟无胶结砂岩的应力响应曲线,若峰前曲线较试验曲线的斜率大,初始刚度偏大,减小颗粒接触刚度再计算,直到与试验曲线吻合。在此基础上,模拟含有胶结物质的砂岩,本文中考虑全胶结砂岩,即设置胶结的颗粒数/模型总接触数[6]=100%、颗粒间的胶结程度[6]α=¯R/RA=1(¯R为胶结平均半径,RA为接触处颗粒中的较小半径),确定平行黏结的刚度须观察及黏结破坏的起始应变值,的峰前曲线较陡且黏结破坏开始的应变较大,说明颗粒间的胶结破坏较晚,减小平行黏结的刚度,颗粒胶结上的应力增大到黏结破坏强度;另外,还须根据黏结破坏的趋势调整平行黏结法向刚度与切向刚度的比例,使应变εa对应的法向和切向黏结破坏数量一致。调整后的应力比和体应变如图4所示。说明该模型模拟胶结砂岩的剪切行为是可行的,可用于后续砂岩力学特性的研究。

图4 应力比和体应变变化曲线对比Fig.4 Comparison of variation curves of stress ratio and volume strain using different methods
由于试验过程不能很好地表征每个颗粒的连接性,鉴于PFC3D程序能从细观角度模拟颗粒的运动特性,模拟4种不同粒度分布对应的颗粒平均连接度(每个颗粒上的接触颗粒个数),如图5所示(最大粒径相同)。图5显示,颗粒的连接度随着颗粒尺寸的增大而增大。粒径较小的颗粒周围有可能未出现接触颗粒,对应的连接度越小,这些颗粒就容易成为“漂浮”颗粒;较小的颗粒与其他颗粒连接时,颗粒间的胶结物质相对较少,射孔试验中由于流体的运动会使该颗粒从砂岩上剥离成为离散颗粒,最终被携带至油井而成为出砂[15]。另外,图5还显示Rmax/Rmin越大,颗粒尺寸相差越大,最大粒径相同时,易“漂浮”颗粒数会增多。由以上分析可知:(1)“漂浮”的颗粒自由度更大,储层开采过程中,流动的油藏更容易携带自由颗粒,根据连接度可知这些“漂浮”的颗粒一般粒径较小,在流体携带作用下,更容易在砂岩骨架中运动;(2)Rmax/Rmin增大使得从砂岩上剥离的砂岩颗粒增多,减少了承担外荷载作用的颗粒数,直接影响了颗粒的接触应力,在相同的外力作用下,由于砂岩颗粒的剥离,原来与之相接触颗粒上的接触力会更大,直接影响了砂岩的力学特性。

图5 不同粒径对应的颗粒接触数Fig.5 Particle connectivity with different particle radius
不同的砂岩粒度分布对其力学特性的影响是不同的,单纯基于随机数学方法生成砂岩颗粒建立的三维数值模型不能准确反映砂岩颗粒的力学特性。特别是胶结砂岩,其受力过程由于胶结物质的存在不同于无黏结砂土介质,其力学响应是胶结物质与砂岩颗粒结构性共同作用的结果。因此,需要根据储层砂岩的实际粒度分布建模以反映砂岩真实的力学响应[6]。
3 粒度分布对砂岩力学特性的影响
基于PFC3D数值模型剪切试验,分析4种不同粒度分布对胶结砂岩的宏观力学响应(应力比、体应变)和颗粒的细观力学响应(配位数、黏结破坏、颗粒转动)的影响。
图6描述了力学参数一定时,4种颗粒分布对岩样应力比和体应变的影响。由图6可知,4种模型计算的应力比均随着εa的增大而增大,初始阶段出现较强的刚性,峰值之后的应变软化很明显,其后软化率随着应变的增大而减小,符合岩体的应力-应变变化规律。由4种计算模型比较可知,Rmax/ Rmin=1.5时的初始刚度最大,且峰值应力也最大,随着应变增大,峰值应力之后的软化应力曲线逐渐趋于稳定,与其他3种计算模型的计算结果有一定的差异,而其他3种模型得到的应力曲线比较相似。其原因在于:Rmax/Rmin=1.5对应的颗粒分布最均匀,且颗粒的中值粒径为2.2 mm,是4个计算模型中最大的,对于光滑砂岩颗粒组成的试样,中值粒径越大的试样其内摩擦角相对越大,初始刚度越大。图6(b)显示4种不同粒度分布对应的峰值应力之前出现了剪缩(正的体应变)和应变软化后出现了剪胀效应。剪胀效应在平行黏结破坏开始之后出现。黏结破坏发生后,一部分颗粒发生转动,颗粒的约束力减小,模型整体的变形增大,总应变也随之增大,这一现象与实际胶结砂岩的力学行为相似。对于4种不同的粒度分布,表现为初始阶段的压缩均较小,但峰后表现出不同的剪胀率。Rmax/Rmin=1.5对应的剪胀效应最为明显,虽然该模型生成的颗粒数与实际颗粒分布的颗粒数接近,由于颗粒粒径的分布范围不同,且中值粒径较大,模型较大的内摩擦角和较均匀的颗粒连接度说明该模型会在黏结破坏之后产生较大的剪胀效应;计算模型3和计算模型4与计算模型1具有相同的中值粒径和最大粒径,且粒径的比值相同,平行黏结破坏之后的体积膨胀具有一定的相似性。
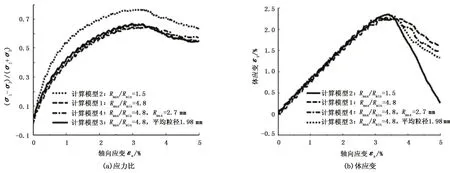
图6 应力比和体应变随轴向应变变化曲线Fig.6 Curves of stress ratio and volume strain varying with axial strain
图7为4种不同粒度分布对应的配位数变化曲线。4条曲线的变化趋势为:初始配位数变化缓慢,随后配位数出现峰值,之后配位数减小的速率增加,符合整个受力过程中颗粒的运动特性;初始压密颗粒接触增多,而后平行黏结破坏,颗粒离散,颗粒接触逐渐减少。计算模型2的配位数最大,其次为实际颗粒分布对应的计算模型1,计算模型4得到的配位数最小,主要在于计算模型2的颗粒半径比较小,颗粒大小均匀,且颗粒的连接性较好,说明在剪切过程中颗粒接触较为充分,大多数颗粒对模型的颗粒接触力起作用,与图7的应力变化相符,而计算模型4对应的颗粒数较少,颗粒不能充分接触,对应的配位数相对较小,越小的配位数越容易产生“漂浮”的颗粒,这些颗粒的自由度较大,更容易在砂岩骨架中运移。
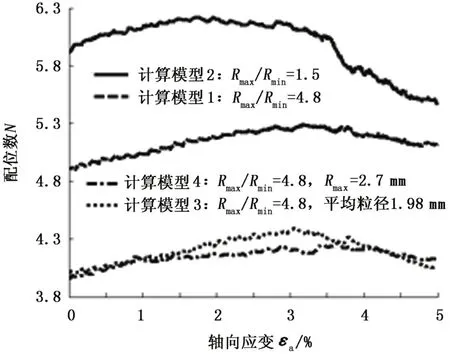
图7 配位数随轴向应变变化曲线Fig.7 Curves of coordination number varying with axial strain
如图8所示的平行黏结变化曲线描述了剪切过程中颗粒黏结砂岩胶结的破坏特征。破坏的黏结在最大峰值应力后迅速增加,说明颗粒之间的黏结破坏越多,黏结破坏的颗粒发生转动,运动时的颗粒间约束就相应减少,与图6、7得出的结论一致。图8显示计算模型2在剪切破坏开始后的平行黏结破坏数增加较多,比其他3个计算模型的黏结破坏数增量要多,虽然与实际颗粒分布的模型具有相同的颗粒数,但颗粒分布曲线相差较大,其剪切破坏有一定的差异,与图6(b)出现的剪胀效应相吻合。另外,计算模型3与计算模型1的平行黏结破坏较接近,主要在于该模型产生的颗粒与实际颗粒尺寸较接近,而计算模型4的黏结破坏数较少,主要在于模型产生的总颗粒数较少,颗粒尺寸相差较大,能黏结的颗粒数也较少,与计算模型1的剪切效应相差较大。由此可见,只有根据实际的粒度分布建立储层砂岩的三维数值模型,才能更准确地描述砂岩受力过程中的力学响应。
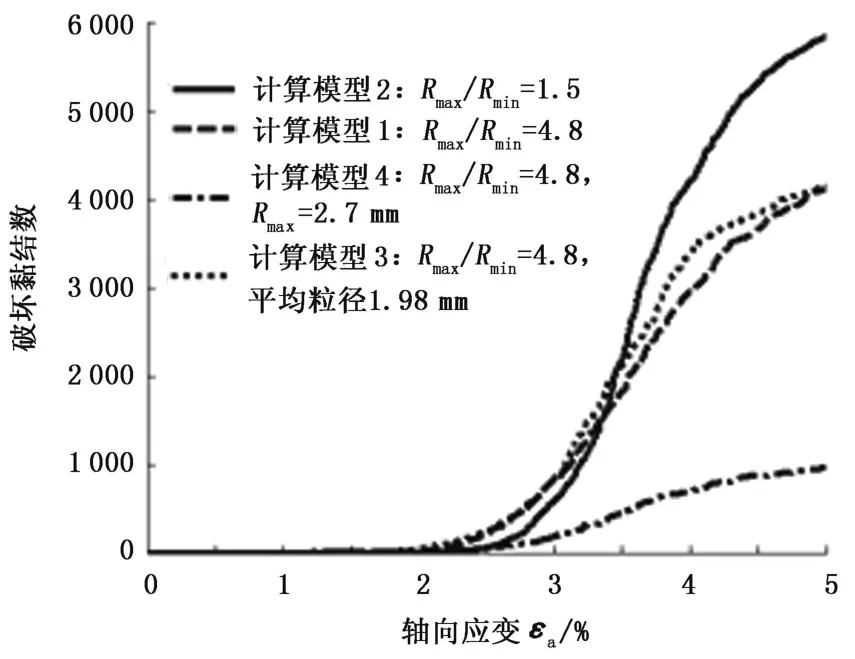
图8 破坏的平行黏结随轴向应变变化曲线Fig.8 Curves of broken-bond varying with axial strain
上述结果描述了剪切过程中砂岩的宏观力学响应曲线,由于室内试验不能有效地表征颗粒的运动特性,图9、10给出了应变为5%时的颗粒黏结破坏和颗粒的转动。图9为移除破坏平行黏结之后的接触网络,即平行黏结破坏后形成的剪切带[14]。4种模型都出现了较为明显的剪切带,计算模型2对应的剪切带较宽,主要在于该模型剪切后出现的黏结破坏数较多,剪切带随之较宽,而计算模型1和计算模型3由于具有较相近的颗粒尺寸,剪切带相差不大,但试验过程中剪切扭转的位置有差异,计算模型1的剪切位置稍微偏上一些。主要原因为外力作用下,全胶结的砂岩试样颗粒间的黏结力较大,剪切过程中需要克服较大的颗粒黏结力,最终才能破坏形成较明显的剪切带,而颗粒的位置分布是有差异的,剪切带的位置也会有差异。计算模型4对应的剪切带方向相反,与上述3个计算模型的力学特性相差甚远,主要在于计算模型4主要由大颗粒组成,类似于级配碎石结构,其模型的破坏主要由颗粒的破坏导致,未出现明显的剪切带,符合脆性岩石力学响应的一般变化规律。图10描述了砂岩颗粒的旋转,4个计算模型在剪切带位置的颗粒转动都较大,且计算模型1和计算模型3中较大颗粒旋转对应的位置较为相似,说明粒度分布相近的模型具有相似的力学响应,计算模型2中的颗粒转动较大值对应的范围大,在主要剪切带附近还有一些颗粒具有较大的转动,与图8、9相吻合,说明黏结破坏后颗粒的约束较小,自由度增大,在流体作用下更容易形成出砂。
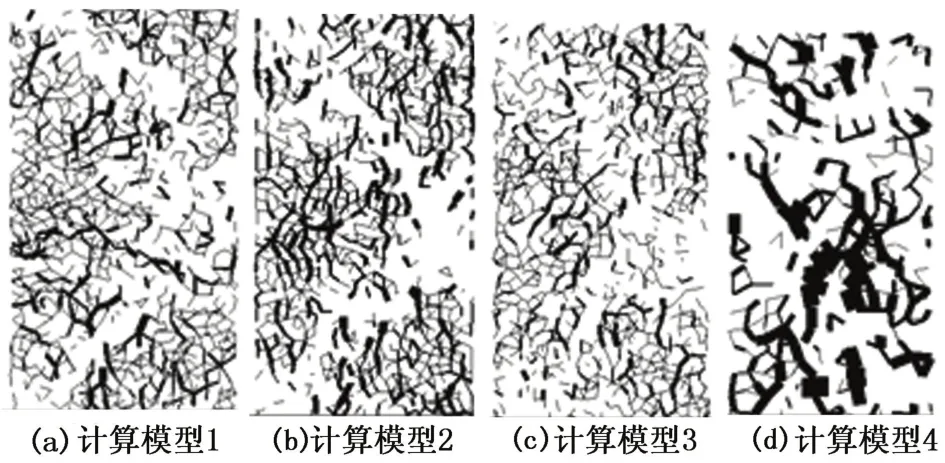
图9 剪切过程的平行黏结变化与接触网络Fig.9 Parallel bond evolution and contact network during shearing for different cases

图10 剪切过程的颗粒转动Fig.10 Particle rotation during shearing
4 结 论
(1)三轴试验得到不同粒度砂岩的力学响应,符合岩石力学响应的一般规律,粒度分布对其力学特性的影响较大。
(2)基于PFC3D的Fish语言引入平行黏结模型,利用胶结的颗粒数与模型总接触数的比值描述胶结物的百分含量,并采用α=¯R/RA确定颗粒间的胶结程度,描述不同类型的储层砂岩是可行的。
(3)与试验结果的比较验证了本文数值模型的可行性。粒径越小则连接度越小,越容易从砂岩中剥离成为“漂浮”颗粒。基于实测的粒度分布曲线建模才能准确反映储层砂岩的力学响应。
(4)颗粒数相近的模型,由于颗粒分布不同,数值模拟的结果与实际粒度分布的计算结果有差异;与具有相同中值粒径的砂岩模型比较,其宏观力学响应相似,但剪切过程中的颗粒配位数差异大,黏结破坏中的颗粒移动过程不同。虽然具有相同的最大粒径和粒径比值,随机生成的颗粒曲线却与实际颗粒的相差较远,得到的力学特征图形也相差甚远。
[1] 龚晓南,熊传祥,项可祥,等.黏土结构性对其力学性质的影响及形成原因分析[J].水利学报,2000(10): 43-47.
GONG Xiaonan,XIONG Chuanxiang,XIANG Kexiang, et al.The formation of clay structure and its influence on mechanical characteristics of clay[J].Journal of Hydraulic Engineering,2000(10):43-47.
[2] 蒋明镜,沈珠江.结构性黏土剪切带的微观分析[J].岩土工程学报,1998,20(2):102-108.
JIANG Mingjing,SHEN Zhujiang.Microscope analysis of shear band in structured clay[J].Chinese Journal of Geotechnical Engineering,1998,20(2):102-108.
[3] 刘海涛,程晓辉.粗粒土尺寸效应的离散元分析[J].岩土力学,2009,30(增刊2):287-292.
LIU Haitao,CHENG Xiaohui.Discrete element analysis for size effects of coarse-grained soils[J].Rock and Soil Mechanics,2009,30(s2):287-292.
[4] 蒋明镜,郑敏,刘芳,等.颗粒级配对火山灰力学特性影响的试验研究[J].扬州大学学报:自然科学版, 2010,13(1):57-62.
JIANG Mingjing,ZHENG Min,LIU Fang,et al.Experiment research on influence of grain size distribution on mechanical properties of volcanic ash in northeast China [J].Journal of Yangzhou University(Natural Science E-dition),2010,13(1):57-62.
[5] 蒋明镜,郑敏,王闯,等.不同颗粒级配的某火山灰的力学性质试验研究[J].岩土力学,2009,30(增2): 64-67.JIANG Mingjing,ZHENG Min,WANG Chuang,et al.Experimental investigation on mechanical properties of a volcanic ash with different grain size gradations[J].Rock and Soil Mechanics,2009,30(s2):64-67.
[6] 刘先珊,董存军.基于三维颗粒流数值模型的胶结砂岩力学特性研究[J].重庆大学学报,2013,36(2): 22-28.
LIU Xianshan,DONG Cunjun.Research on mechanical characteristics of the cemented sandstone based on 3-dimensionalPFCnumericalmodel[J].Journalof Chongqing University,2013,36(2):22-28.
[7] 尹小涛,郑亚娜,马双科.基于颗粒流数值试验的岩土材料内尺度比研究[J].岩土力学,2011,32(4): 1211-1216.
YIN Xiaotao,ZHENG Yana,MA Shuangke.Study of inner scale ratio of rock and soil material based on numerical tests of particle flow code[J].Rock and Soil Mechanics,2011,32(4):1211-1216.
[8] 唐娴,戴经梁.基于颗粒流程序的沥青混合料颗粒接触模拟[J].郑州大学学报:工学版,2009,30(1): 111-114.
TANG Xian,DAI Jingliang.Simulation of particle contact of asphalt mixture based on particle flow code[J].Journal of Zhengzhou University(Engineering Science), 2009,30(1):111-114.
[9] PFC3D 3.10.三维颗粒流程序[M].3版.明尼苏达州:明尼苏达大学,2005.
[10] YANG Budong,JIAO Yue,LEI Shuting.A study on the effects of microparameters on macroproperties for specimens created by bonded particles[J].International Journal for Computer-aided Engineering and Software, 2006,23:607-631.
[11] DAVID O P.Simulating stress corrosion with a bondedparticle model for rock[J].International Journal of Rock Mechanics&Mining Sciences,2007(44):677-691.
[12] Jung-Wook P,Jae-Joon S.Numerical simulation of a direct shear test on a rock joint using a bonded-particle model International Journal of Rock[J].Mechanics& Mining Sciences,2009(46):1315-1328.
[13] 任怀强,刘金华,杨少春,等.吐哈盆地红台地区辫状河三角洲砂岩储层微观特征[J].中国石油大学学报:自然科学版,2008,32(5):12-17.
REN Huaiqiang,LIU Jinhua,YANG Shaochun,et al.Sandstone reservoir m icroscopic characteristics of braid delta of Hongtai area in Tuha Basin[J].Journal of China University of Petroleum(Edition of Natural Science), 2008,32(5):12-17.
[14] 孙其诚,辛海丽,刘建国,等.颗粒体系中的骨架及力链网络[J].岩土力学,2009,30(s1):83-87.
SUN Qicheng,XIN Haili,LIU Jianguo,et al.Skeleton and force chain network in static granular material[J].Rock and Soil Mechanics,2009,30(s1):83-87.
[15] 刘先珊,许明.基于三维流固耦合模型的油井出砂细观机理研究[J].岩土力学,2013,34(8):2363-2370.
LIU Xianshan,XU Ming.Micromechanism of sand production in oil well based on 3-dimensional coupled fluidsolid model[J].Rock and Soil Mechanics,2013,34 (8):2363-2370.
(编辑 沈玉英)
Effects of particle size distribution on mechanical characteristics of cemented sandstone
LIU Xianshan1,2,XU Ming1,2
(1.School of Civil Engineering,Chongqing University,Chongqing 400045,China; 2.Key Laboratory of New Technology for Construction of Cities in Mountain Area,Chongqing University, Ministry of Education,Chongqing 400045,China)
For sand production in the sandstone reservoir,the meso-structure plays an important role in the dislodgement of the sand particles.The cemented sandstone as a case study,four numerical models considering different particle size distribution based on 3D particle flow code(PFC3D)were developed to simulate the mechanical response in the shearing test.In addition,the stress ratio,volume strain,coordination number and broken bonds changing with the axial strain were analyzed.The results show that the particle size distribution has great influence on the mechanical characteristics of the sand,so the numerical model based on random method to generate particles cannot completely represent the physical structure of the practical sandstone.Therefore,the numerical model based on measured particle size distribution can correctly describe the mechanical response of the reservoir sandstone.The smaller particles have less connectivity with other particles,so the particles with more freedom more likely become the dislodged particles when extracting.
meso-structure;cemented sandstone;particle size distribution;3D particle flow code;mechanical characteristics
TU 45
A
1673-5005(2014)05-0142-07
10.3969/j.issn.1673-5005.2014.05.020
2013-12-28
国家重点基础研究发展计划“973”项目(2014CB046903);国家自然科学基金项目(51478065,51109231);中央高校基本科研业务费项目(106112013CDJZR200004,106112014CDJZR200014)
刘先珊(1978-),女,副教授,博士,主要从事岩土力学及数值计算方面的研究。E-mail:lzmoumou@163.com。
刘先珊,许明.粒度分布对胶结砂岩力学特性的影响[J].中国石油大学学报:自然科学版,2014,38(5): 142-148.
LIU Xianshan,XU Ming.Effects of particle size distribution on mechanical characteristics of cemented sandstone[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(5):142-148.
