步枪弹侵彻带软硬复合防护明胶靶标的数值模拟

罗少敏,徐诚,陈爱军,张晓云,刘苏苏

(1.南京理工大学机械工程学院,江苏南京 210094;2.南京理工大学理学院,江苏南京 210094)

步枪弹侵彻带软硬复合防护明胶靶标的数值模拟

罗少敏1,徐诚1,陈爱军2,张晓云1,刘苏苏1

(1.南京理工大学机械工程学院,江苏南京 210094;2.南京理工大学理学院,江苏南京 210094)

为研究步枪弹撞击带软硬复合防护明胶靶标的作用过程和作用机理,采用显式有限元方法对7.62 mm步枪弹侵彻复合靶标过程进行数值模拟,分析侵彻过程中的典型现象及明胶靶标动态响应。数值计算结果表明:陶瓷锥的形成是由压缩应力波和拉伸应力波共同作用的结果;弹头加速度变化存在明显的分段与拐点,侵彻陶瓷面板过程中,加速度达到最大,侵彻聚乙烯(PE)背板层时,出现第二个拐点;由于防护层存在多个界面,撞击过程中PE背板界面存在速度多峰现象:当弹头运动加速度达到最大时,PE背板界面出现第一个速度峰,明胶界面出现第一个压力峰;当弹头开始侵彻PE背板时,背板层出现第二个速度峰;在步枪弹撞击过程中明胶内压力波传递呈现球形波基本形态,压力峰值随距离增加呈指数衰减。

兵器科学与技术;枪弹;数值模拟;软硬复合防护;明胶;侵彻

0 引言

现代战场枪弹与破片对士兵的威胁最大,由硬质防弹插板和软质防弹衣组成的软硬复合防护成为最主要的单兵防护具。一般情况下,步枪弹的速度达到700～980 m/s,在该速度段内针对步枪弹对带软硬复合防护的有生目标作用效应的研究具有重要的现实意义和工程应用价值。

关于步枪弹撞击软硬复合防护的研究,国内外主要集中在步枪弹直接侵彻陶瓷及侵彻陶瓷面板与背板组成的复合防护层,研究侵彻全过程动态响应和防护层防护能力。Krishnan等[1]研究了陶瓷/高聚乙烯(UHMWPE)复合板的抗弹性能,以数值模拟对比弹道穿深实验验证了有限元网格的精细程度对计算结果的影响,分析了弹头对陶瓷/高聚乙烯复合板的侵彻过程,为单兵防弹衣的毁伤预测提供了参考。Feli等[2-3]研究了枪弹侵彻陶瓷—纤维复合材料过程,认为随着弹头初始速度的减小陶瓷锥最大角度增大,同时随着初始速度的增加,纤维凹面层数增多,顶部复合板的变形减小。Fawaz[4]等基于Hypermesh和LS-DYNA平台研究了陶瓷复合防护的侵彻响应,认为在有角度侵彻比垂直侵彻,破坏更为严重,为防护材料的优化提供了合理的依据。但上述研究未直接涉及到步枪弹对软硬复合防护后的有生目标作用效应。由于有生目标的特殊性和复杂性,对其作用效应的研究难以直接进行,国内外通常采用明胶靶标来模拟。带软硬复合防护的明胶靶标是弹道实验和评估步枪弹对带防护有生目标的作用效应的主要靶标,目前国内外未见采用数值模拟研究步枪弹对带软硬复合防护的明胶靶标作用效应相关文献报道。

本文结合相关弹道实验,建立了与之对应的有限元数值计算模型,利用显式有限元方法进行数值模拟,再现了7.62 mm步枪弹对带软硬复合防护的明胶靶标的侵彻过程。数值计算结果与实验结果吻合较好,验证了所建立的有限元模型的正确性。在此基础上,研究侵彻过程中典型物理现象和非贯穿侵彻时防护后明胶靶标动态响应,为非贯穿侵彻带软硬复合防护有生目标的毁伤机理认识、评估,枪弹优化设计以及单兵防护装备优化设计提供了参考。

1 数值计算模型及实验验证

1.1 有限元模型

本文研究的带软硬复合防护明胶靶标几何结构如图1所示,它由陶瓷面板、聚乙烯(PE)背板和高聚乙烯纤维软防护层及明胶组成。陶瓷轻质高强防弹插板为PE材料陶瓷复合板,由高性能PE纤维“UD”无纬布和氧化铝陶瓷材料构成,符合美国NIJ标准防Ⅲ级,规格尺寸为250 mm×300 mm.软质防护为超高分子量聚乙烯纤维防弹材料,符合GA141-2001警用标准防Ⅱ级。明胶材料为4℃、10%弹道明胶,作为仿生肌肉靶标,在制作过程中,将插板和软防护与明胶材料一起脱模。本文主要研究7.62 mm步枪弹对该带软硬复合防护明胶靶标的作用效应。

对图1所示靶标进行有限元网格划分,离散化后有限元网格如图2(a)所示,为兼顾计算时长与计算精度,对防护层和明胶块中心弹着点区域进行进一步细化:面板、背板层和软防护在弹着点中心5倍半径区域加密,向外划分逐渐稀疏,面板和背板中心区域划分30段,如图2(b)所示;弹头由弹头壳被甲、铅套和钢芯组成,弹头壳锥部与圆柱部过渡部分由3个单元转化为2个单元,铅套前部精细划分,钢芯部分由头部向尾部逐渐稀疏,如图2(c)所示。弹头、陶瓷面板层、PE背板层和明胶块采用SOLID单元,其中弹头中弹头壳共 9 792个单元,铅套共10 400个单元,钢芯共9 216个单元;陶瓷面板共63 000个单元;PE背板共126 000个单元;明胶块共180 000个单元。软防护共46层,采用Shell单元建模,中心加密方式与面板和PE背板一致,共165 600个单元。

数值模拟中边界条件设置与实验一致,弹头壳、铅套与钢芯设置自动面面侵蚀接触,靶板与软质防护以及明胶块之间设置为自动面面接触,陶瓷插板面板层与背板层之间设置固连失效接触,实验中软防护层与层之间无胶粘材料,因此软质防护内部设置自动单面接触,弹头与复合靶标之间设置面面侵蚀接触,整体采用单点积分,明胶块设置沙漏控制。

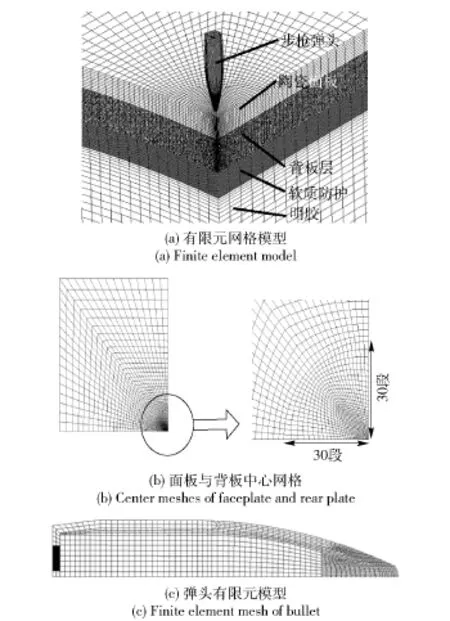
图2 弹头侵彻靶板及明胶有限元网格Fig.2 Finite element mesh of bullet impacting armor and gelatin

1.2 材料模型与参数

弹头的被甲、铅套和钢芯采用Johnson-Cook模型结合Gruneisen状态方程来描述弹头在侵彻过程中材料的力学行为,其材料参数与文献[5]相同。陶瓷面板采用Johnson-Hoimquist模型来描述,根据文献[6-7]来进行主要参数的赋值。描述背板和软防护的材料性能都采用 MAT_COMPOSITE_ FAILURE_OPTION_MODEL材料模型,对于PE背板采用SOLID单元,对于软防护采用SHELL单元。该模型由Cheng等[8]嵌入LS-DYNA软件中,是包含8种失效模式的正交异型材料模型,根据所做基础材料实验及文献[9]确定主要材料参数值。表1给出了PE背板采用的材料模型参数,表2给出了PE纤维软防护的材料模型参数。明胶靶标采用流体弹塑性材料模型(MAT_ELASTIC_PLASTIC_HYDRO)结合LINEAR_POLYNOMIAL状态方程来描述,材料参数参考文献[10-11],与文献[5,12]相同。

1.3 模型验证

为验证本文所建立有限元仿真模型的可信性和准确性,进行了7.62 mm步枪弹侵彻带软硬复合防护的明胶靶标实验。实验中采用的软硬复合防护靶标结构尺寸与图1相同,入靶速度由光电测速靶测量,明胶内压力由压电晶体传感器测量,高速摄像机拍摄弹头与防护及靶标作用过程。下面从实验后弹头结构形态和穿深、背凸量、最大压力、明胶靶标瞬时凹入量等方面将计算结果与实验结果进行了比较。

表1 PE背板材料主要参数Tab.1 Mechanics properties of materials of PE

表2 软防护材料主要参数Tab.2 Mechanics properties of materials of so ft armor

数值仿真结果和实验结果皆显示步枪弹均未穿透防护:步枪弹穿过陶瓷面板,继续侵彻PE背板层,最终停留在插板背板层中。如图3所示,弹头作为投射物在撞击过程中受到防弹插板阻碍,不断破碎及变形,弹芯头部墩粗,呈明显的“蘑菇”形,计算的弹头形态与实验结果基本一致。

表3给出了计算获得的典型侵彻特征量与实验结果的比较,可知计算获得的步枪弹穿深、剩余长度、明胶中压力峰值以及明胶靶标最大瞬时凹入量等与实验结果基本一致。综合计算与实验对比情况可知,本文所建立的有限元模型具有较好的可信度和准确性,能够有效地模拟杀伤元对软硬复合防护后的明胶靶标的侵彻作用和动态响应。

图3 弹头形态对比Fig.3 Comparison of bullet configurations

2 计算结果分析

2.1 侵彻过程中防护层应力变化特性

弹体撞击陶瓷面板,产生一束压力波,压力波在横向和纵向方向传播,弹着点及其附近区域开始产生损伤,如图4中10 μs时刻。纵向压力波沿弹道方向传播,到达陶瓷面板与PE背板界面处时,由于陶瓷材料和高聚乙烯材料的密度和声阻抗等性质的差异,会反射形成一个拉伸波,被压缩的固体材料会膨胀,拉伸波与弹体前进方向反向传播,不同材料界面开始出现损伤,当时长在30 μs时,陶瓷锥基本形成。图4描述了典型时刻段防护材料应力分布情况。反射拉伸波在陶瓷面板内不断传播,陶瓷锥不断扩展,至弹头停止运动。

在由硬质插板和软质防护材料组成的防护体系中,插板防护对弹头的侵彻阻滞和动能消耗起主要作用。弹头在界面击溃过程中材料流动发生质量侵蚀和变形,损耗部分动能,同时受到靶板阻力作用,侵彻速度下降,直至被拦截停止运动。弹头与软硬复合防护接触全过程,伴随了陶瓷击溃、弹头变形、背板背凸变形、软质防护变形和明胶靶标动态凹陷等主要物理现象。在侵彻过程中,陶瓷材料受到拉压应力波的反复作用发生裂纹扩展、破碎及飞溅,如图5所示。通过靶板z向应变云图与等值线可以看出,拉伸损伤和压缩破坏对陶瓷锥的影响很大,陶瓷锥中心区域由于受到压缩应力波作用出现负应变,在陶瓷锥边沿区域由于受到反射拉伸波的作用出现正应变,应变云图与陶瓷锥基本形态相似。背板层与弹头直接接触时,阻挡弹头继续侵彻,发生变形,压缩软质防护层变形,同时明胶靶标受到撞击产生凹陷,弹头直接侵彻结束后明胶靶标发生长时间动态卸载消耗传递至模拟靶标的能量。

表3 数值模拟结果与实验结果对比Tab.3 Comparison of numerical and experimental results

2.2 弹靶相互作用过程中速度、加速度变化特性

弹头速度变化、加速度的变化与整个侵彻过程中陶瓷面板、PE背板的物理特性相关,与陶瓷锥的成型、背板的变形直接相关。图6给出了计算所获得的弹头侵彻带软硬复合防护的明胶靶标过程中速度曲线和加速度曲线,在弹头速度衰减曲线上标出了3个特征点:A0点为运动初始接触点,B0点为弹头部分即将穿过陶瓷面板与背板接触时刻,C0点为运动速度为0时刻。

在加速度曲线上,A1点为运动初始点,B1点为加速度最大点,在C1点时加速度曲线出现第二个拐点,D1点加速度值减小为0.根据图6和图4,将弹头侵彻过程和加速度变化分为3段:

1)A1B1段,约为0～20 μs,弹头头部与陶瓷面板初始接触,加速度急剧增大,弹头头部材料向外流动而发生质量侵蚀和变形。在弹头界面击溃过程中,陶瓷面板受到高速冲击作用,开始出现初始裂纹,在头部“挤进”陶瓷面板后,加速度达到最大,此阶段视为弹头侵彻过程的开坑阶段。开坑部分直径大于弹头直径。

2)B1C1段,约为20～50 μs,陶瓷面板由于短时间的强冲击破碎,对弹头的阻力减小,后期主要以摩擦阻力为主。在此阶段内陶瓷锥形成,弹头与陶瓷锥一起运动,同时受到背板阻力与面板摩擦力作用,加速度减小。此阶段可视为弹头在陶瓷面板内运动的稳定侵彻阶段,速度曲线上的B0点与B1C1曲线段上的C1点很接近。

3)C1D1段,约为50～90 μs,在C1点,加速度曲线出现第二个拐点,弹头头部部分嵌入PE层压板内部,弹头主要受到背板阻力作用,加速度逐渐衰减,直至减小为0.速度曲线上的C0点与C1D1段上的D1点不重合。随着弹头的运动PE背板的变形成为主要的吸能方式,背板背凸量增大直至弹头停留在背板内,同时弹芯发生墩粗,整体长度变短。

弹头在侵彻过程中主要包括:界面击溃、弹芯墩粗变形、磨损发热等。弹头变形主要发生在约前50 μs:在弹头界面击溃阶段,弹头头部锥头部分磨损侵蚀,弹头形状和质量发生改变,与靶板接触面积变大;在弹头受到背板防护阻力作用过程中,弹头的变形对侵彻的影响较为明显,伴随弹芯墩粗和质量侵蚀,侵彻速度下降,同时会发生加速度的跳跃,如B1C1曲线段较为明显的跳跃点。

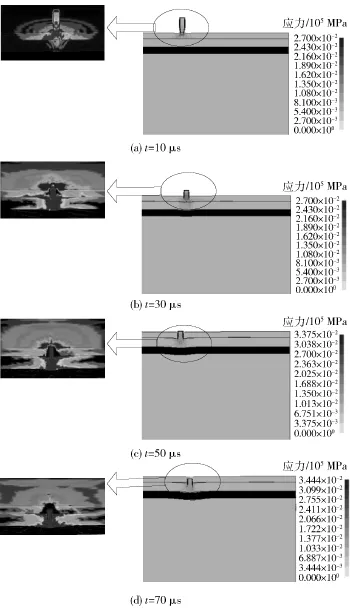
图4 侵彻过程典型时刻Fig.4 Penetration processes at some typical moments

图5 靶板z向应变云图(t=30 μs)Fig.5 Strain contour of ceramic/PE composite target in direction z(t=30 μs)

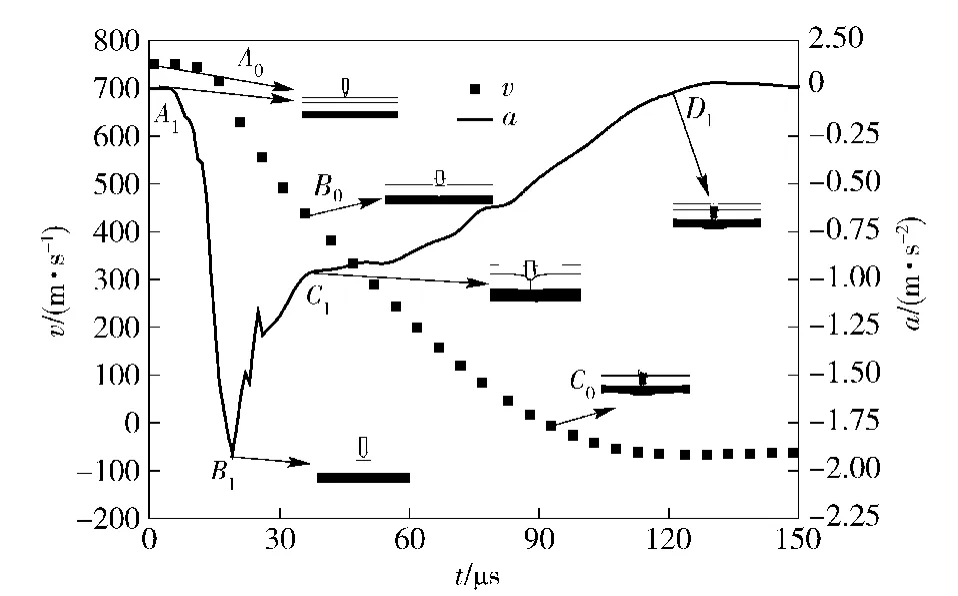
图6 弹头速度和加速度变化曲线(v0=734 m/s)Fig.6 The variation of projectile velocity and acceleration(v0=734 m/s)

2.3 靶标界面速度变化特性

在整个侵彻过程中靶标存在3个界面,其中两个明显界面:一是插板防护与软质防护之间;二是软质防护与明胶靶标之间。一个不明显界面,即插板防护中陶瓷面板与PE背板材料之间。分析界面位置处单元及质点的速度、加速度对于研究非贯穿侵彻作用下明胶靶标的损伤机制尤为重要。

数值模拟中在弹头弹道方向上选取PE背板与软质防护、软质防护与明胶靶标界面处单元,分析明胶靶标在侵彻过程中的动态特性。与软防护接触的PE背板单元为71 986,与软防护接触的明胶靶标单元为354 809,图7为背板及明胶界面速度变化曲线,可以看出明胶界面单元的最大速度为66.8 m/s, PE背板单元运动的最大速度为87.3 m/s.

如图7所示,背板界面存在速度多峰。对比图6,背板界面单元第一个速度峰值点出现的时间约在20 μs左右,与弹头加速度最大值出现的时刻基本一致。背板速度第一个峰值的出现与弹头的强冲击直接相关:弹头撞击陶瓷面板层,在此过程中出现第一个速度上升沿并达到最大;在形成陶瓷锥后,弹头与陶瓷锥一起运动,继续运动过程中伴随陶瓷的破碎,对弹头的阻力开始减小,出现“卸载”现象,但随着弹头到达PE背板,与PE背板接触,PE背板的速度增大出现第二个峰值。软防护最后一层与明胶界面单元第一个速度峰值时刻出现一定延迟,这与冲击过程中压力波的传递有关,同时由于防护层变形,软防护最后一层会挤压明胶界面使得明胶界面速度出现第二个平缓峰值,随后明胶界面与软防护最后一层开始出现明显的界面分离。

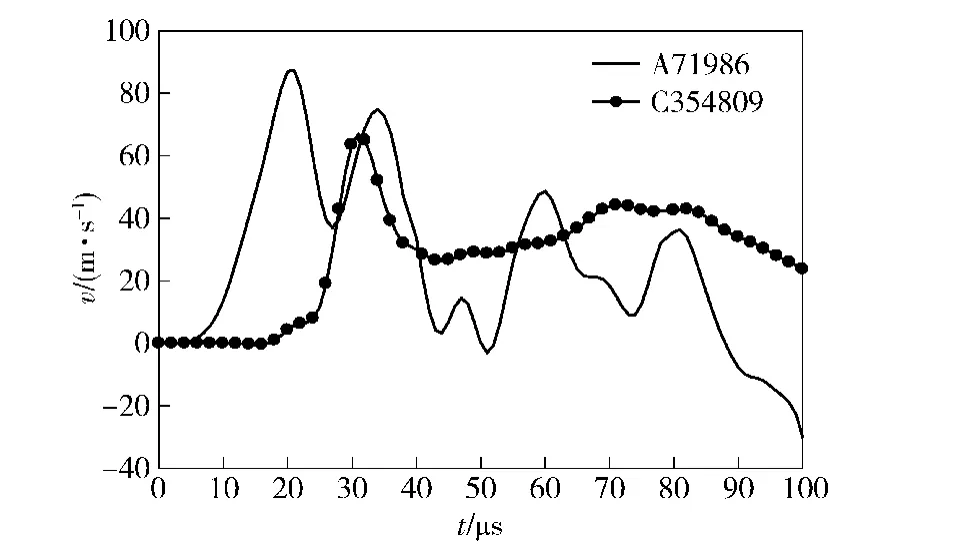
图7 界面单元速度变化Fig.7 The variation of interface velocity

2.4 明胶内压力波传递特性

在撞击过程中,当弹头接触防护材料,压力波形成,传递至界面,形成拉伸波。压力波继续经由软质防护传播至明胶模拟靶标,如图8所示,在传播初始阶段,明胶靶标内典型时刻压力波传递呈现球形波基本形态。沿弹头侵彻方向每隔2 cm选取明胶上单元,共4个测点,测点压力随时间变化曲线如图9所示。

计算获得的明胶界面压力峰值达到94.1 MPa,界面压力曲线会出现第二个压力峰值,这是由于弹头与PE背板撞击所致;压力波在明胶内传播速度为1 421.5 m/s,实验中测得传播速度为1 501 m/s,二者基本一致。压力峰值随距离衰减情况如图10所示,压力波在传播过程中,随着传播距离增加,压力峰值呈指数下降。

3 结论

本文针对步枪弹侵彻带软硬复合防护的明胶靶标,进行了有限元建模和数值模拟,通过与实验结果的对比验证了有限元模型的可信性和准确性,计算结果表明:

1)弹头在撞击过程中,弹头加速度存在明显的分段与拐点。侵彻陶瓷面板过程中,加速度达到最大,侵彻PE背板层时,出现第二个拐点。弹头变形主要发生在侵彻陶瓷面板运动过程中,侵彻背板时主要吸能方式为PE背板的拉伸变形。

图8 明胶内压力波传递Fig.8 Propagation of shock waves in gelatin

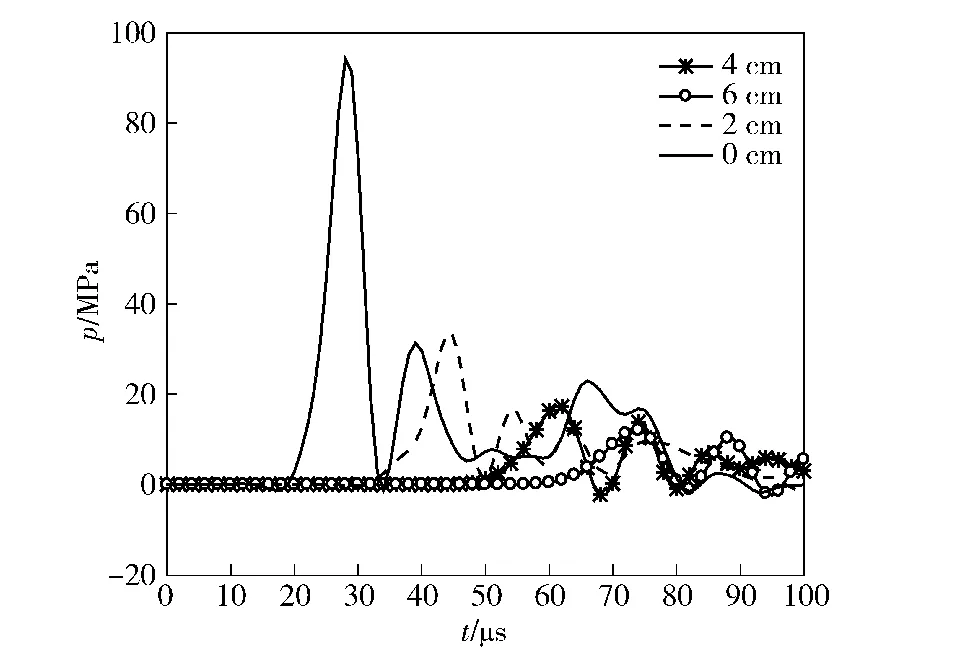
图9 不同距离测点处压力波形曲线Fig.9 Pressure of shock waves at different distances

2)由于靶标存在多个防护层界面,撞击过程中PE背板界面点存在速度多峰现象,出现时刻与弹头运动存在一定的关联。当弹头运动加速度达到最大时,在弹头强冲击下,背板材料背面弹道方向单元速度达到第一个速度峰,随后明胶界面出现第一个压力峰,最大压力达到94.1 MPa,防护层界面处明胶单元最大运动速度达到66.8 m/s.当弹头开始进入背板层时,PE背板第二个速度峰,导致明胶压力曲线出现第二个峰值。

3)冲击过程中,明胶内压力波传递呈球形波形态,压力峰值随传播距离呈指数规律衰减。

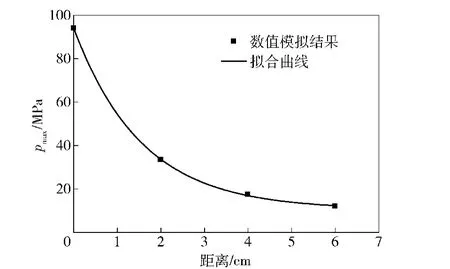
图10 压力峰值随距离变化情况Fig.10 Peak pressure versus distance

References)

[1] Krishnan K,Sockalingam S,Bansal S,et al.Numerical simulation of ceramic composite armor subjected to ballistic impact[J]. Composites,2010,41:583-593.

[2] Feli S,Asgari M R.Finite element simulation of ceramic/composite armor under ballistic impact[J].Composite Structures,2011, 42(4):771-780.

[3] Feli S,Asgari M R.An analytical model for perforation of ceramic/multi-laryered planar woven fabric targets byblunt projectiles [J].Composite Structures,2011,93(2):548-560.

[4] Fawaz Z,Zheng W,Behdinan K.Numerical simulation of normal and oblique ballistic impact on ceramic[J].Composite Structures, 2004,63(2):387-395.

[5] 温垚珂,徐诚,陈爱军,等.步枪弹侵彻明胶靶标的数值模拟[J]兵工学报,2013,34(1):14—19.

WEN Yao-ke,XU Cheng,CHEN Ai-jun,et al.Numerical simulation of penetration of bullet on gelatin target[J].Acta Armamentarii,2013,34(1):14-19.(in Chinese)

[6] Simha C H M.Computational modeling of the penetration response of a high-purity ceramic[J].International Journal of Impact Engineering,2002,27(1):65-86.

[7] Cronin D S,Bui K,Kaufmann C,etal.Implementation and validation of the Johnson-Holmquist ceramic material model in LS-Dyna[C]//4th European LS-DYNA Users Conference.Ulm,Germany:DYNA more Gmh,2003:D-I-47-D-I-59.

[8] Cheng W,Hallquist J.Implementation of three-dimensional composite failure model into DYNA3D[M].US:Livermore Software Technology Corporation,2004.

[9] Menna C,Asprone D,Caprino G,et al.Numerical simulation of impact tests on GFRP composite laminates[J].International Journal of Impact Engineering,2011,38(8/9):677-685.

[10] Segletes S B.Modeling the penetration behavior ofrigid spheres into ballistic gelatin,ARL-TR-4393[R].Aberdeen Proving Ground,MD:Army Research Laboratory,2008.

[11] Kwon J,Subhash G.Compressive strain rate sensitivity of ballistic gelatin[J].Journal of Biomechanics,2010,43(3):420-425.

[12] Wen Y K,Xu C,Wang H S,et al.Impact of steel spheres on ballistic gelatin at moderate velocities[J].International Journal of Impact Engineering,2013,62:142-151.

Numerical Simulation of Bullets Penetrating into Gelatin Target with Hard/Soft Composite Armor

LUO Shao-min1,XU Cheng1,CHEN Ai-jun2,ZHANG Xiao-yun1,LIU Su-su1
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China; 2.School of Science,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

In order to explore the interaction process and mechanism of bullet impacting a gelatin target with hard/soft composite armor,the penetration of 7.62 mm bullet into composite armor and gelatin is numerically simulated using an FEA method,and the typical phenomena of impacting process and the dynamic response of gelatin target are analyzed.The simulation results show that the formation of the ceramic cone results from the compressive and tensile stress waves.The obvious segmentation and inflection points display on the curve of projectile acceleration.The acceleration reaches its maximum when the projectile penetrates into a ceramic faceplate.The second inflection point appears when the projectile penetrates into PE rear plate.The multi-peaks appear on the velocity curve of PE rear plate due to multiple interfaces on protection layer:When the projectile reaches the maximum acceleration,the first peak appears,and the first pressure peak appears on gelatin interface;the second peak appears when the projectile penetrates into PE rear plate.The propagation of pressure wave in gelatin presents the basic form of spherical wave,and the pressure peak propagation complies with the law of exponential decay.

ordnance science and technology;bullet;numerical simulation;hard/soft composite armor; gelatin;penetration

TJ012.4

:A

:1000-1093(2014)08-1172-07

10.3969/j.issn.1000-1093.2014.08.006

2013-10-25

罗少敏(1987—),男,博士研究生。E-mail:1119lsm@163.com;徐诚(1962—),男,教授,博士生导师。E-mail:xucheng62@mail.njust.edu.cn