纯距离目标跟踪中的观测站机动航路优化研究*

王 璐 刘 忠

(海军工程大学电子工程学院 武汉 430033)

纯距离目标跟踪中的观测站机动航路优化研究*

王 璐 刘 忠

(海军工程大学电子工程学院 武汉 430033)

纯距离测量条件下,对于静止目标,单观测站必须进行机动转向才可观测,根据可观测矩阵,提出可观测度的概念,推导出观测站一次转向机动时的优化航路,即观测站转向前后航向角度差为(观测站一次转向)。仿真结果表明,优化航路在定位精度、稳定性和跟踪速度方面性能方面最佳。

纯距离; 可观测度; 航向角; 优化航路

Class Number O231

1 引言

纯距离目标跟踪定位问题又称为纯距离目标运动分析,是通过获取运动目标的距离信息,并利用这些随时间变化的距离序列来实时估计目标运动参数的技术[1～4]。目前纯距离定位估计算法方面的研究较少,主要是因为:理论上,纯距离问题具有较强的非线性;实际中,纯距离问题应用领域较少。

近年来随着水下无线传感器网络技术的发展,使得对纯距离目标运动分析问题的研究越来越迫切。如在水下无线传感器网络的节点定位过程中,携带GPS的AUV通过测量其与节点之间的到达时间差,获得一系列含噪声的距离值,进而估计静止节点或移动节点的状态参数,此时若选择其他的测量方法,则要为每个节点配备额外的设备,不符合节点体积小、能耗低的特点。因此,研究纯距离运动分析问题具有一定的理论和现实意义。

在单站纯距离目标运动分析中,首先需要研究的是如何解决系统的可观测性问题。研究表明,纯距离测量条件下,对于静止目标,单观测站必须进行机动转向才可观测[5],即观测站机动航路与系统的可观测性条件密切相关。现有机动航路优化的文献主要是针对纯方位目标跟踪进行研究的[6～9],尚无纯距离系统航路优化问题的研究。本文利用单站纯距离系统的可观测矩阵给出可观测度的概念,在令可观测度最大的基础上推导纯距离测量条件下观测站进行一次转向机动时的优化航路,并进行仿真实验。仿真结果表明,航路优化对定位与跟踪精度有很大的影响,选择优化的机动航路可以进一步改善定位与跟踪算法的性能。

2 纯距离系统描述

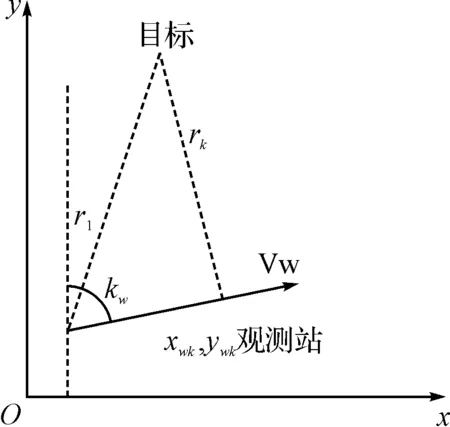
图1 单观测站纯距离目标运动分析示意图

观测站作匀速直线运动,速度为Vw,航向角为Kw,进行k次观测,采样间隔为T,观测站的位置坐标依次为(xw1,yw1),(xw2,yw2),…,(xwk,ywk);目标静止,位置坐标为(x,y);rk为k次观测时目标与观测站间的距离,dk为k次观测时观测站与坐标原点的距离,r为目标与坐标原点的距离,坐标系如图1所示。在上述条件下,列如下方程:

(1)

(2)

x2+y2=r2

(3)

上述方程组联立,可以得到:

(4)

该方程组可记为AX=B。

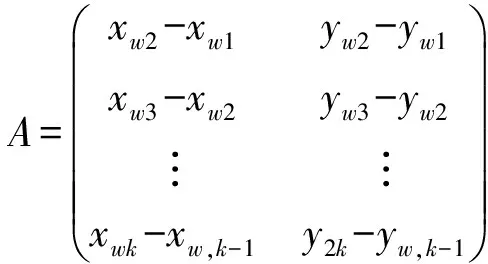
M=ATA,M为二阶矩阵,则有MX=ATB,设:

(5)

其中:

(6)

(7)

方程组MX=ATB有唯一解的充要条件是系数矩阵(可观测矩阵)和增广矩阵的秩相等,且等于未知向量的维数,即R(M)=R(M|ATB)=2。

3 优化航路

对于静止的目标,观测站必须转向机动才可观测。假设观测站在l(1

则可观测矩阵

(8)

以往研究仅以detM是否等于0来判断系统的可观测性,并没有一个可以判别系统可观测性强弱的量。这里,我们定义可观测度ρ=detM来进行可观测程度的定量描述。

4 仿真计算

假设目标静止,位置坐标为(500m,1000m),观测站初始位置(2000m,2000m),测量时间间隔为1s,共进行次仿真试验,测距误差服从均值为0,均方差为10m的高斯白噪声。选择以下三种不同机动航路,运用最小二乘算法[10]进行仿真实验。

航路1(观测站转向15°):观测站作匀速直线运动,v=16m/s,航向角Kw1=π/6,50s后观测站进行一次转向,以航向角Kw2=π/4继续匀速直线运动,速度不变。

航路2(观测站转向60°):观测站作匀速直线运动,v=16m/s,航向角Kw1=π/6,50s后观测站进行一次转向,以航向角Kw2=π/2继续匀速直线运动,速度不变。

航路3(观测站转向90°):观测站作匀速直线运动,v=16m/s,航向角Kw1=π/6,50s后观测站进行一次转向,以航向角Kw2=2π/3继续匀速直线运动,速度不变。

图2 X轴坐标估计

图3 Y轴坐标估计

在仿真过程中,针对观测站转向15°(航路1)、转向60°(航路2)和转向90°(航路3)三种机动航路,对静止目标的定位跟踪进行了比较,仿真结果表明:观测站一次转向90°的机动航路的定位精度、收敛速度优于转向和转向的航路,且观测站在转向前,对静止目标是不可观测的,转向后位置曲线开始收敛,进一步验证了针对静止目标观测站必须转向才可观测的结论。

5 结语

在纯距离测量条件下,针对静止目标,观测站必须机动才可观测,本文根据可观测矩阵提出可观测度的概念,并推导出观测站一次转向时的机动优化航路。仿真结果表明,观测站一次转向时定位精度、收敛速度最佳,即选择优化的机动航路可以提高系统可观测度和改善定位与算法性能。针对运动目标和观测站多次机动的纯距离航路优化问题还需要进一步研究。

[1] Taek L S. Observability of Target Tracking with Range-only Measurement[J]. IEEE Journal of Oceanic Engineering,1999,24(3):383-387.

[2] WANG Lu, LIU Zhong. Research on Observability of Non-Maneuvering Target Tracking Based on Multiple Observers Range-Only[C].(ICITMI2012). Guang Zhou,2012:744-748.

[3] Branko R, Sanjeev A, James M. Target Motion Analysis Using Range-Only Mearurements Algorithm, Performance and Application to ISAR Data[J]. Signal processing,2002,24:273-296.

[4] 孙仲康,郭福成,冯道旺.单站无源定位跟踪技术[M].北京:国防工业出版社,2008:21-29.

[5] 梁玥,刘忠.单站纯距离定位与跟踪系统可观测性分析[C]//火力与指挥控制2008年学术会议论文集.太原:火力与指挥控制研究会,2008:292-297.

[6] S E Hammel, P T Liu. Optimal Observer Motion for Location with Bearings Measurements[J]. Computers Maths Applic,1989,18(1):171-180.

[7] J P Helferty, D R Mudgett. Optimal Observer Trajectories for Bearings-Only Tracking by Minimizing the Trace of the Cramer-Rao Lower Bound[C]//32th International Conference of Control and Decision,1993:936-938.

[8] 赵建昕.纯方位目标定位与跟踪航路优化模型[J].火力与指挥控制,2010,35(11):106-108.

[9] 石章松.纯方位目标跟踪中的观测器机动优化研究[J].计算机仿真,2010,27(1):334-337.

[10] 梁玥,刘忠.静止目标纯距离测量下的定位原理与方法研究[J].指挥控制与仿真,2009,31(4):26-29.

A Study of Observer Maneuvering Optimal Trajectory in Range-Only Target Tracking

WANG Lu LIU Zhong

(College of Electronic Engineering, Naval University of Engineering, Wuhan 430033)

Only when the observer is in divertical motion, the target can be observed in the single-station range-only conditions. For the observability matrix, the observable degree is given, and the optimal trajectory of the observer is deduced, that is the difference of the observer’s course angle (it means the observer make ninety degree turns). The simulation result indicates that the optimal trajectory of the observer has better location precision、stability and tracking velocity than other trajectory.

range-only, observable degree, course angle, optimal trajectory

2014年4月3日,

2014年5月27日

王璐,女,博士研究生,讲师,研究方向:目标定位与跟踪、系统建模与仿真。刘忠,男,教授,研究方向:目标运动分析、最优控制。

O231

10.3969/j.issn1672-9730.2014.10.011