SOLAS概率破舱稳性及计算结果分析

徐彦哲

（中船重工船舶设计研究中心有限公司，大连 116000）

SOLAS概率破舱稳性及计算结果分析

徐彦哲

（中船重工船舶设计研究中心有限公司，大连 116000）

以SOLAS 2009规范为基础，结合Napa软件对一货船概率破舱计算结果的分析，提出优化极限GM曲线的若干方法，并对于残存因数等于零的破损状态处理方法做了详细的介绍。

SOLAS2009；Napa；极限GM曲线；残存因数

0 引言

国际海事组织海上安全委员会的第 82届会议通过了 SOLAS第Ⅱ-1章修正案的决议MSC.216(82)。该决议与之前通过的决议MSC.194(80)将确定性的客船SOLAS90标准与干货船基于概率方法的SOLAS92标准协调为统一的概率破损稳性要求，为船舶设计提供了新方向和思路，也更具灵活性，但同时要求也大幅提高。

Napa软件的前身是芬兰瓦锡兰船厂开发的软件，于1989年独立正式成立。作为总体开发设计的主流软件，拥有很多设计模块和功能，如静水力计算、舱容计算、装载稳性计算、完整稳性计算和破舱稳性计算等。准确合理利用Napa的各功能，可以高效准确地解决问题，尤其在概率破舱稳性计算方面有着强大的优势，不仅能通过二次开发编写宏命令正确快速地算出结果，而且也能够运用一系列的命令和图表分析计算结果。

1 规范解读

根据SOLAS第Ⅱ-1章B-1部分第5-1条4，需要确立ds、dp、和dl三种吃水的最小GM曲线，这就要求进行概率破舱稳性的计算。在给定的初始工况和根据分舱得到的一系列破损工况下，通过计算使达到的分舱指数A大于或等于要求的分舱指数R，且每一部分指数对客船不小于0.9R及对货船不小于0.5R，则船舶的分舱可视为足够，从而得到不同吃水下的极限 GM曲线。如整个营运纵倾超过±0.5%LS时，在超出部分的基础上按步长不超过1%LS所获得的若干纵倾计算相应的极限GM曲线，然后再结合完整稳性的极限GM曲线，最终得到极限GM曲线的包络线。

对于民用货船来说，船长80m及以上的B型干舷货船和根据国际载重线公约可减小干舷但拟载运甲板货的货船都要进行概率破舱稳性的计算。一般的不载运甲板货的B型干舷散货船一般较容易满足规范的要求，但对于集装箱船等主要载运甲板货的船型来说，概率破舱算出的极限GM值则是至关重要的，因为这关系到甲板货物的装载量，直接影响船舶的经济性。

2 实例分析

本文对一条拟装运甲板货的货船的概率破舱计算进行研究，分析SOLAS概率破舱稳性计算中一些问题的解决方法以及如何准确有效地计算极限GM值。

主尺度确定之后，在根据船舶的使用功能要求制定好分舱方案，做好Napa中的总布置、开口定义和分区表等一些计算前的设置。利用命令“GEM DAM SUB=ZONES…”来生成破损工况并与之前定义好的初始工况做成计算表格。定义初始工况的时候，各个吃水下初始GM值的选取可根据初步装载计算，选取较为理想并在合理范围内的值。这里将前期的定义和计算的中间过程省略掉，只讨论计算结果。

分舱指数的计算结果如下，并如表1所示。

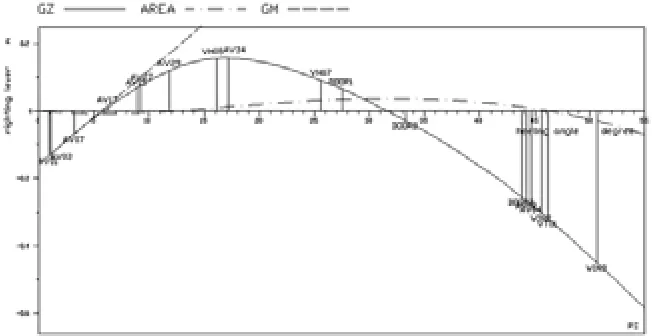
由以上可以看出，A

表1 概率破舱稳性计算结果

1）调整装载工况，在满足纵倾、螺旋桨浸没率、驾驶室可视范围以及最小首吃水的要求下使轻载营运吃水尽量减小，这样同时降低了部分吃水（dp），对计算结果一般是有利的。

2）检查特定的破损状态，观察破损后的静稳性曲线，是否淹没了非水密的开口，从而导致残存因数Si=0。如果有非水密的开口被淹没，那么升高相应的开口高度也可以提高分舱指数。

3）提高最深分舱吃水（ds）和部分吃水（dp）下的GM值，效果是显而易见的，但是过高的GM值对甲板装货量是很不利的。

提高分舱指数也有很多其它的方法，比如增加横贯进水装置、连通边舱等，视具体的情况各种方法达到的效果也是不同的。本文主要介绍第二种方法，即是针对残存因数为零的情况。由于 Si=0的CASE也是相当多的，逐一检查存在较大的工作量，本文推荐使用一种新的检查方法，即横向比较和纵向比较。

运行概率破舱计算程序之前，可以把所有的开口关闭掉（IRO ALL），运行之后得到另一个分舱指数，这个指数比考虑开口作用得到的指数大。把两个得到的分舱指数进行每一分项的比较，比如分别比较单区破损下的三个吃水，分别比较二区或者多区破损下的三个吃水，称之为横向比较（表1）。假如在单区破损情况下的最深分舱吃水得到的分舱指数相差的比较多，那么可以从此项开始入手，来进行纵向比较。把开口考虑进去，运行破舱稳性计算的宏，计算好之后利用以下命令组得到如表2所示的结果。

这里需要分析SFACSOL=0（残存因数=0）的破损CASE，参照SOLAS规范第II-1章B-1部分第7-2条，对于货船，残存因数为Sfinal，计算公式如下：

表2 单区破损DS吃水下的计算结果

式（1）有三个关键的参数：K、GZmax和Range，其中：K与进水阶段的平衡横倾角有关，与表2中得KSOL对应；GZmax是θv角范围内最大正复原力臂，不得取为大于0.12m，与表2中GZMAXSOL对应；θv是任何进水阶段复原力臂变负的角度，或者不能风雨密关闭的开口被水浸没的角度；Range是从进水阶段的平衡横倾角量取到正复原力臂的范围，正值范围取为到达θv的角度，不得取为大于16°，与表2中的RANGESOL对应。

将表2的结果与不考虑开口作用得到的类似结果进行纵向比较，对于某一CASE，例如DS/P7.2.0，如果考虑开口作用得到的残存因数等于 0，但是不考虑开口作用得到的残存因数大于 0，那么就要分析这个CASE。如果GZMAXSOL或者KSOL等于0，那么除了增加初始GM以外只有通过重新分舱或者加水密分隔才能提供分舱指数。如果GZMAXSOL和K都不等于0，那么一般是破损后淹没了非水密开口（如空气管）导致的SFACSOL=0。对于这样的破损CASE，利用以下命令组得到表3中的结果（这里计算的是左舷破损）。

LQ DROP, CASE, STAGE, SIDE, NAME, X, Y, Z, IMMA, IMMR

LIS DROP DS/P7.2.0 OPE=(UNP WEA) SOP=(A)

UNP和WEA分别代表无保护开口和风雨密开口，也就是非水密的开口。

主要检查IMMR一项，其表示开口点到水线面的垂向距离，如果是负值，那么表示此开口已经被淹没。也可以用图形的方法来检验，使用命令PLD DCR DS/P7.2.0画出稳性曲线以及上面的开口（图1），如果开口显示在破损后静稳性曲线上(GZ曲线)平衡位置的左边，那么也表示开口已经被淹没。表3中开口AV05对应的IMMA值为“-”，表示左舷的这个开口早已经被淹没，但在图1中是显示不出来的。右舷的开口也显示为“-”，但不表示被淹没。总之，只需要考虑表3中IMMR为负值的开口就可以了。找到被淹没的开口之后，根据计算适当提高这些开口的高度可以达到提高分舱指数的目的。一般情况下只计算一舷（PS or SB），所以对称的开口也要提升。

需要特别注意的是，有些定义好的开口没有在表3中或者图1中出现，这就表示和这些开口连通的舱已经破损，作为失效的开口不予考虑。

同理可以检验其它的吃水状态或者多区破损的情况。还需注意RANGESOL也用于计算残存因数，与不能风雨密关闭的开口的高度和位置有关，可助于分析残存因数比较小的CASE。

表3 相关典型开口的计算结果

图1 破损后的稳性曲线

在实际设计建造过程中，有时空气管的开口高度提升的太高会影响船舶的甲板及以上的布置或者装卸货的操作，很多船东从船舶的使用性和美观性来考虑也不希望设置太高的空气管。因此此种方法和增加初始GM值的方法可以结合来使用，力求达到一个设计平衡点，在满足功能要求前提下，尽量优化设计。

3 结束语

基于对规范的深入研究，并结合Napa软件的一些功能对于概率破舱稳性计算结果的检验是很有帮助的。规范是基础，Napa软件作为一种有效的设计工具需要灵活运用。本文只是抛砖引玉，关于Napa其它有助于设计的功能还需要在工作中逐步来发掘。另外也可以看出，对于一种结果的检验，可以通过不同的角度采取不同的方法，而且几种方法可以相互检验，最终取得合理结果。

[1] INTERNATIONAL MARITIME ORGANIZATION. SOLAS CONSOLIDATED EDITION 2012[S]. 2012.

[2] 中国船级社. SOLAS 2009分舱与破损稳性要求实施指南[M]. 北京: 人民交通出版社, 2009.

[3] 盛振邦, 杨尚荣, 陈雪深. 船舶静力学[M]. 哈尔滨:哈尔滨工程大学, 2003.

[4] NAPA MANUALS[M]. 2012-1.

Analysis of SOLAS Probabilistic Damage Stability and the Calculation Result

Xu Yan-zhe
(China Ship Design & Research Center Co., Ltd., Dalian 116000, China)

This paper analyzes several methods to optimize the minimum GM curve based on the analysis of the result of probabilistic damage stability calculation of a cargo ship by Napa program in accordance with SOLAS convention 2009 and describes how to handle the damage cases when survival factor equals to zero.

SOLAS2009; Napa; limit GM curve; survival factor

U662.1

A

1005-7560(2014)01-0001-04

徐彦哲（1983-），男，工程师，主要从事船舶总体设计以及船型开发工作。