力平衡式加速度传感器的性能评价方法*

2014-07-05杨黎薇周正华崔建文刘琼仙

地震研究 2014年2期

杨黎薇，周正华，崔建文，刘琼仙

(1.云南省地震局，云南昆明650224;2.南京工业大学，江苏南京210009)

0 前言

强震动观测通过对强震仪记录数据的处理分析进一步研究地震动特性，进而为工程抗震设防及防震减灾提供基础依据。准确可靠的加速度记录不仅可用于估算地面倾斜、反演震源过程，还可用来评估震害，为强震观测研究领域的扩展提供基础数据(胡聿贤，2006)。

为使获取的强震动记录更精确，国内外研究领域主要集中于改进力平衡式加速度传感器的设计，即根据工作原理和理论计算，从设计方面去完善力平衡式加速度传感器的性能技术，以国家制定的技术规范去开展实验测试，通过实测数据和实验曲线来评价仪器的可用性。可见，探寻某种方法去定期检测加速度传感器的性能指标，在保证仪器记录数据准确性方面很有意义。

本文通过数字强震动仪功能试验，研究SLJ－100型力平衡式加速度传感器的动力特性，继而提出基于功能试验的力平衡式加速度传感器的性能评价方法。该测试方法可以对在网运行的加速度传感器进行在线质量测试，能够指导强震动台站工作人员自行进行传感器性能测试，对强震动观测的实际工作有一定的参考性。

1 力平衡式加速度传感器简介

力平衡式加速度传感器采用现代传感技术机电一体化设计，将差容位移检测器与力平衡技术相结合，设置了“标定线圈”，使检测和标定工作更加方便。成熟的力平衡式加速度传感器设计一般采用激励信号调制、解调，加入力反馈进行电压输出的模式。输出电压的大小与电容极板运动的加速度成正比，即电容中间极板的输出电压就是传感器壳体的运动加速度(杨黎薇，2010)。换言之，力平衡式加速度传感器是将3个轴向的加速度振动真实情况转换成电压信号输出，来实现对各种低频或超低频的振动测量。

力平衡反馈技术可以弥补普通传感器的机械特性缺陷，减小弹性部件的非线性失真或灵敏度阈值。我国自主研发SLJ－100型三分量力平衡式加速度计灵敏度高、动态范围广、频带宽且线性范围大，可广泛应用于各地区强震动台网，其主要技术指标见表1(数字强震动加速度仪，DB/T 10—2001)。

如图1所示，SLJ－100型三分量力平衡式加速度传感器工作时，加速度传感器受外部加速度影响后，其内部摆体M产生位移使电容C值改变，再经过传感器内的位移检测放大器KA与伺服放大器KS共同产生并输出一个与被测加速度成正比的电压VS，该电压经KL驱动记录器输出并由反馈系统进一步传送至摆线圈GF，产生的电磁反馈力矩使摆体M恢复到原来的平衡状态(王家行，胡振荣，1997，1998)。由于深度负反馈，作用在内部摆体M上的不平衡力(惯性力与反馈力之差)极小，可认为反馈力与惯性力接近平衡，进而可得到输出电压与被测加速度之间的关系(王之芳，1996)。

表1 SLJ－100型三分量力平衡式加速度传感器主要技术指标Tab.1 The major technical indicators of SLJ－100 threecomponent force balance accelerometer transducer

图1 SLJ－100型力平衡式加速度传感器设计原理图Fig.1 Design principle diagram of SLJ－100 force balance accelerometer transducer

SLJ－100型力平衡式加速度传感器实质上是一个具有深度负反馈的伺服系统，比起一般的开环测量系统，能更好地改善传感器的测量精度和稳定性，采用负反馈装置，在一定程度上可提高传感器的动态响应，适当增加工作系统刚度，并可展宽传感器的工作频带。同时，其内部设置有标定电路，便于对加速度传感器的自振频率和阻尼进行实时检查(李彩华，2005)。

达朗贝尔原理用静力学中研究平衡问题的方法来研究动力学问题，亦称为动静法。假设质量为m的非自由质点M，在主动力和约束力作用下沿曲线运动，则该质点的动力学基本方程为ma=F+FN，可见，达朗贝尔原理指的是在质点运动的每一瞬时，作用于质点的主动力、约束力和质点的惯性力在形式上构成平衡力系。

根据达朗贝尔原理，质点的达朗贝尔原理可直接推广至质点系，即在质点系运动的任一瞬时，作用于每一质点上的主动力、约束力和该质点的惯性力在形式上构成平衡力系。将加速度计摆体质量块视为质点系，可知加速度计摆体质量块受到外部介质产生加速度X(t)后产生的运动微分方程式为(曲家骐，王季秩，1998)

其中，θ(t)为加速度计摆体质量块以转轴O为中心点偏离平衡位置后形成转角大小;Jm为以转轴O为中心点形成的加速度计摆体质量块转动惯量;bm为以转轴O为中心点构架的阻尼力矩系统;Km为弹簧常数;G为以转轴O为中心点加速度计摆体质量块在单位电流输入驱线圈时产生的电磁旋转力矩，常数值，量纲为［Nm/A］;I(t)为放大器输入驱动线圈产生反馈电流;M为加速度计摆体质量块;l为转轴O与摆体质量块中心点间距;X(t)为外部介质产生加速度;Kmθ(t)为弹簧对加速度计摆体质量块产生的恢复力矩;MlX(t)为外部介质产生加速度后形成的惯性力矩。

闭环反馈系统中，输入驱动线圈中的电流I(t)为

式中:K为与电气参数相关常数值;KC为灵敏度系数(V/m);KS为放大倍数;lC为电容极板中心与旋转轴间指示摆长;B为反馈放大比例常数值;KT为微分放大时间常数值。

式(2)代入式(1)可得

如图2所示，SLJ—100型三分向加速度传感器经伺服放大后的输出电压为U0(t)，此电压可表示为

阻尼常数D由两部分构成，D=DM+DE。其中，DM为加速度传感器实际产生的阻尼常数;DE为反馈电路电流作用于加速度传感器内驱动线圈产生的阻尼常数。

式中，力平衡加速度传感器自振的圆频率n值由闭环反馈系统中电气参数决定。由于力平衡式加速度传感器自振的圆频率与弹簧刚度Km和转动惯量Jm有关，同时也与各电气参数相关，通常GKKCKSlCB＞＞Km，故可将传感器自振的圆频率简化为

(6)式中，力平衡加速度传感器的折合摆长与加速度计摆体质量块、转轴O与摆体质量块中心点间距及转动惯量均有关(李科杰，2002)。n为加速度传感器自振的圆频率;D为阻尼常数;lr为折合摆长。

将(6)、(7)、(9)代入式(5)简化得

图2 SLJ－100型三分向力平衡式加速度传感器受力运动模块Fig.2 Force motion module of SLJ－100 three-component force balance accelerometer transducer

2 功能试验响应及自振特性确定

SLJ－100型三分量力平衡式加速度传感器可近似看成为二阶系统(李科杰，2002)，即根据试验中正弦输入信号与阶跃输入信号这两种标准输入信号下的响应特性去分析系统的动态变化，其常微分方程为

式中:ωn为无阻尼固有角频率、ζ为阻尼比值、k为系统的静态灵敏度。

功能试验主要是根据仪器电流的采样率进行，通过该试验可了解强震动仪传感器的工作状态。由于力平衡式加速度传感器的动态响应与数字滤波器的动态响应相互联系，要将该传感器的响应单独分开进行定量解释非常困难，为消除数字滤波器响应对传感器响应的影响，直接获取力平衡式加速度传感器的响应，通常需要很高的采样率(1 000次/秒以上)。

激励是加速度由零时刻变化到某常数值的瞬时变化，SL－100型力平衡式加速度传感器功能试验是测试两组输入方波(图3)激励下的反应(图4)，试验中输入电流在1～10 mA之间。其响应分为两部分，通常称为去阻尼响应和有阻尼响应。去阻尼响应是在第一个输入脉冲工作衰减至极限时开始进行，至第二个输入脉冲工作前，去阻尼恰好完成;有阻尼响应则是从第二个脉冲开始工作后至实验完成。

图3 功能试验输入波形Fig.3 The input waveforms in functional test

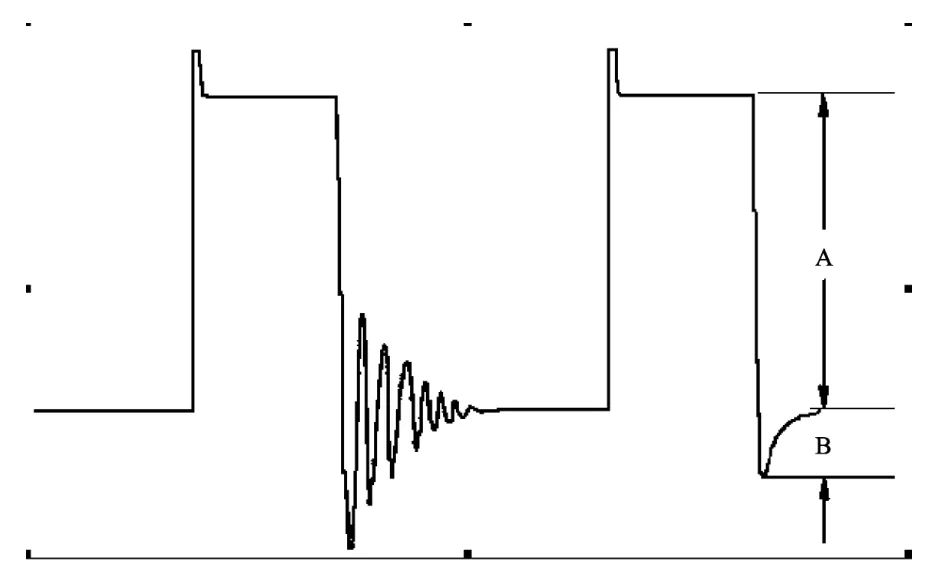
图4 功能试验曲线Fig.4 The curve of functional test

强震动仪的动态特性优劣程度主要由固有频率ωn或共振频率ωd决定，对阻尼比值ζ的恰当选取也可改善强震动仪的动态特性。试验中，动态响应振荡衰减的快慢常用过冲响应比表示，它表示阶跃曲线超过稳态值的最大峰高与阶跃响应稳态值的比值。功能试验响应结果表明，固有频率ωn越高，功能试验去阻尼部分响应振荡越剧烈。恰当设置阻尼比值可减小过冲量、加宽幅頻特性的平直段，提高仪器的动态特性。对于特定的力平衡式加速度传感器功能试验数据可依据下述方法确定其固有频率ωn(杨黎薇，2010)。

假定功能响应的去阻尼响应n个波峰或波谷间的时间为t，则在阻尼比值为ζ'的情况下，系统频率为ωd=2π(n－1)/T，据此可以确定小阻尼固有频率通常 ζ'≈0.02，则有 ωn≈ωk。

图4显示，固有频率ωn越高，响应曲线上升越快;阻尼比值ζ增大，过冲现象会减弱。由于在稳态响应值上下取±10%误差时，ζ=0.6的响应曲线建立时间最短;在稳态响应值上下取±5%误差时的响应曲线最佳。因此，由采集加速度计在阻尼比值为0.6～0.7之间的实验数据绘制的响应曲线可知，过冲响应比越小越好。同时，功能试验响应结果表明，随阻尼比值ζ增大，功能试验响应的有阻尼响应的过冲响应越小，即图3中所示的B值越小。通常采用过冲响应比来描述阻尼比值ζ的影响。

式中:a为过冲响应比，A为阶跃响应曲线的稳态值，B为超过阶跃响应曲线稳态值的最大峰值。本文以自振频率为50 Hz的力平衡式加速度传感器为例，讨论了阻尼比值ζ对过冲响应比a的影响，分析计算了不同阻尼比值ζ情形下的过冲响应比，结果见表2。

从表2可见，阻尼比值ζ从0.60增大至0.70这一过程中，过冲响应比a由9.5%逐渐递减为4.6%。对固有频率在80～200 Hz的力平衡式加速度传感器进行类似反应分析，发现固有频率对过冲响应比a的影响很小可以忽略为零。

试验中，与阶跃响应曲线有关的动态响应指标主要反映在时间常数τ、上升时间Tr、建立时间Ts及过冲响应比a等方面。分析试验结果，最大过冲响应比又受到阻尼比值、输入信号上升时间和传感器自振频率的影响。时间常数仅用于一阶系统中，它对强震动仪的动态响应特性影响极小。根据强震动仪完成一个高精度响应来确定强震动仪的阻尼比值，适当延长阶跃响应曲线由稳态值的10%上升为90%的上升时间，将会减小过冲响应比值，有利于改善强震动仪的动态性能。上升时间是指在这个阶段的时间，上升时间越短，过冲量会越大。由于加速度计的自振频率只与其自身固有特性相关，自振频率越高，过冲量会越小，同时，阻尼比值越大，过冲量越小。

如果过冲响应比保持在0.5，即B为A一半的情况下，强震动仪的动态性能是最佳状态。即当阻尼比值为0.67、0.68、0.69和0.70，过冲量分别为5.9、5.4、5.0和4.8时，强震动仪有较好的动态特性。

将表2中力平衡式加速度传感器的阻尼比值与计算过冲响应比间的关系成曲线(图5)。进行力平衡式加速度传感器的功能试验时，可依据试验数据确定出过冲响应比a，再根据图5及表2，用内插法确定出加速度传感器的阻尼比值ζ。

表2 阻尼比值ζ在0.60～0.70间产生过冲响应比Tab.2 Overshoot response ratio produced in damping ratio ζ between 0.60 ～ 0.70

3 强震动仪的频率响应及性能分析评价

幅频特性与相频特性之间存在一定的内部联系，用频率响应表示强震动仪的动态特性时，主要是用幅频特性描述。输入波为正弦波信号时，对力平衡加速度计的动态性能多采用以下指标来表示:一是通频带;二是工作频带;三是相位误差。强震动仪的动态特性主要用幅频特性与相频特性来表征，其幅频特性与相频特性可由系统频率响应确定(李科杰，2002)。

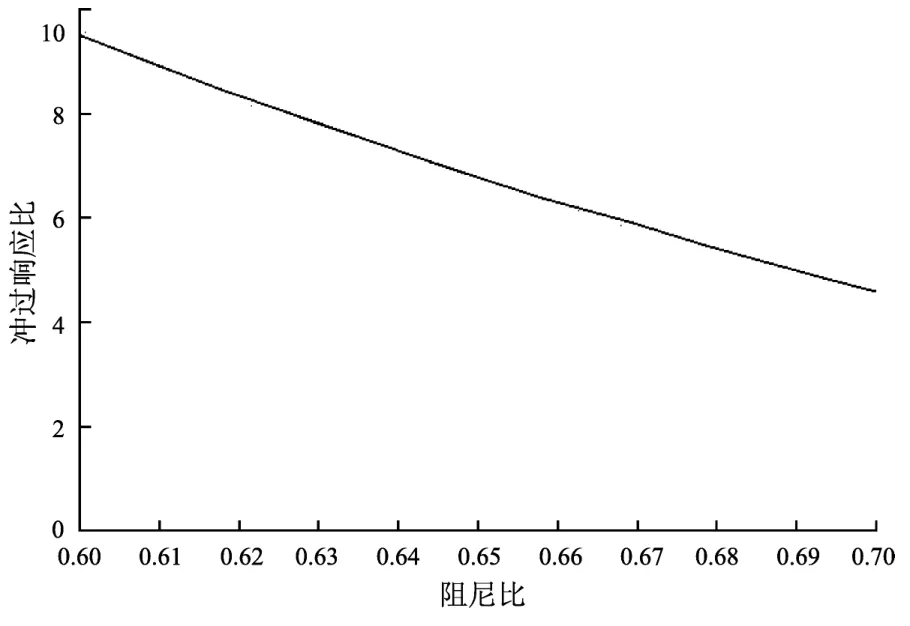
图5 阻尼比值与过冲响应比的关系变化Fig.5 Changes of relationship between damping ratio and overshoot response ratio

对公式(11)作拉普拉斯变换可得

其中:Y(s)、X(s)分别为y(t)、x(t)的拉普拉斯变换，s为复变量。式(13)可整理为

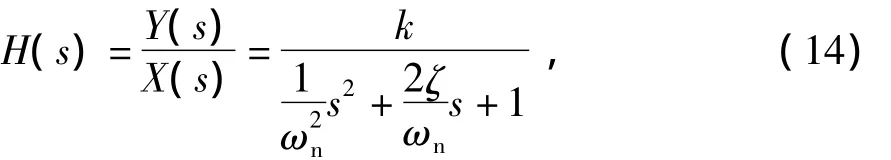
其中，H(s)为传递函数，继而可得到频响函数为

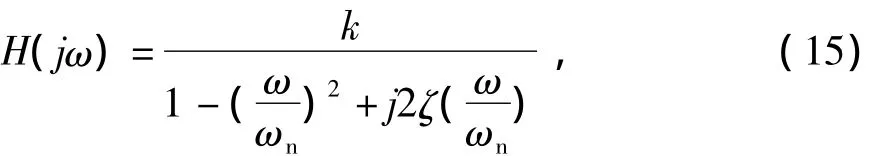
由式(15)可导出幅频响应A(ω)和相频响应φ(ω)，且依据式(16)和式(17)计算出f=50 Hz时，阻尼比值 ζ在 0.55、0.60、0.65、0.68、0.70和0.75时对应产生的频率响应，并对幅频响应曲线进行归一化处理，见图6(Cyril，Allan，2007)。

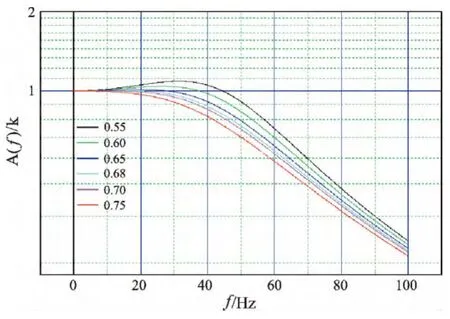
图6 幅频响应变化曲线Fig.6 Amplitude frequency response variation curve

图6中，当加速度传感器的阻尼比值ζ为0.65或0.68时，仪器的幅频曲线平坦段最长，其幅频特性最佳。当仪器的幅频响应下降至－3 dB，即A(f)/k=0.707为允许误差时，应根据该允许误差去确定整个系统的有效频带。由图6可知，随着加速度传感器的阻尼比值ζ增大，有效频带会相对变窄，当阻尼比值ζ＞0.70后，仪器的幅频响应直接下降至－3 dB以下(李德葆，陆秋海，2004)。因此，对特定的加速度传感器的性能校准工作来讲，若按传感器的幅频响应平坦性要求，必须将加速度传感器的阻尼比值设定在0.65≤ζ≤0.70范围内(李海亮，2000)。

在已知工作频带范围内，相位误差大小应控制在5°～10°。从不同阻尼比值对应的相频响应曲线变化中，找到相频曲线的失真度，即可确定相频特性可用误差范围。图7黑线表示加速度传感器的完全线性相位曲线，分析表明，加速度传感器的阻尼比值ζ由0.65依次递增至0.75时，传感器的相位变化越加接近线性。

分别对功能试验中阻尼比值为0.55、0.60、0.65、0.68、0.70和0.75的相频响应数据进行最小二乘线性拟合，通过试验数据点与其拟合程度得到相关系数R，若R值接近±1，则表示试验数据相关度高，拟合程度好，具体计算数据见表3。

图7 相频响应变化曲线Fig.7 Phase-frequency response variation curve

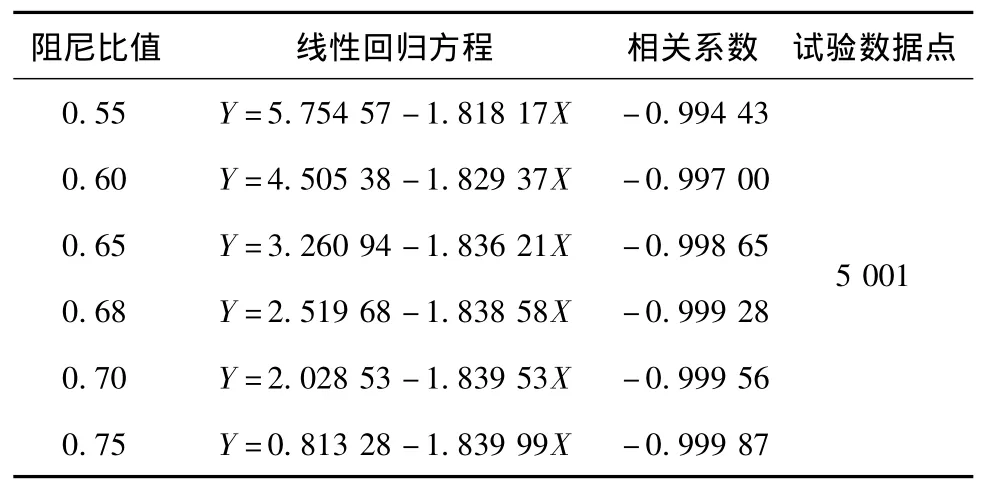
表3 不同阻尼比值功能试验数据相频响应线性拟合Tab.3 Phase-frequency response linear fitting of the data obtained by the different damping ratio functional tests

已知第i个测量数据点与拟合直线间偏差值为Δi=yi－(a+bxi)，其中i=1，2，3，…，5 001 。根据不同阻尼比值的最大偏差Xmax与平均偏差X，求，计算出最大失真度为最大偏差与最大输出相位值比×100%，即可分析评价仪器相频响应的线性特征，具体计算结果如表4所示。

表4 不同阻尼比值功能试验数据相频响应失真度分析Tab.4 Phase-frequency response distortion degree analysis of the data obtained by the different damping ratio functional tests

相位是否呈线性状态与相关系数R、最大偏差值、平均偏差值有关。分析表3和表4数据可知，仪器的阻尼比值从0.55增大到0.75时，相关系数从－0.994 43逐渐增大为－0.999 87，即阻尼比值增加，其相位线性特征越来越明显;根据最大偏差值与平均偏差值计算出值也由1.494 1逐渐增大为2.226 9，即值越大，相位越趋于线性变化。由相位变化趋势可知，随着阻尼比值由0.55增大为0.75时，相位的失真度由5.006%减小为1.318%。可见，仪器阻尼比值越大，相频响应曲线越不易失真。

图8 相位差随频率变化的关系曲线Fig.8 The curve of phase difference varies with frequency

图8表示在不同的阻尼比值下，各相频响应曲线与完全线性相位之差的变化关系曲线。当阻尼比值ζ=0.55时，其相频响应曲线与完全线性相位之差接近9°，随着阻尼比值缓缓增大，产生的相频响应曲线与完全线性相位之差逐步减少，当阻尼比值ζ=0.75时，其相频响应曲线与完全线性相位之差仅是1°。根据传感器的相频响应特性要求，非线性相位与线性相位差在3°以内，其产生的系统相频响应误差可忽略不计。因此，仪器阻尼比值设置为0.68≤ζ≤0.75范围内较合适。

以相频响应曲线特征为依据评价强震动仪的工作性能，需保证相位失真度在5%范围内，由试验可见，阻尼比值为0.68、0.70和0.75的相频响应曲线几乎可完全线性化，其中，阻尼比值0.75的响应曲线线性化最佳。因此，SLJ－100型力平衡式加速度传感器的阻尼比值选择在0.68～0.70范围内最佳。

4 实例分析

通过实际工作中某一SLJ－100型力平衡式加速度传感器的功能试验，功能试验曲线如图9所示，使用性能评价方法对其进行性能评价，并以此实例说明评价方法可行性。

由去阻尼响应振荡曲线(图9中左侧的振荡曲线)可得到峰值与峰值间的时间t=0.020 1 s，并计算出传感器的固有频率为fn=49.75 Hz，由传感器固有频率标称值50 Hz可知，传感器的固有频率变化较小。依据有阻尼响应可得过冲响应B=0.259，阶跃脉冲响应A=5.01，可由式(12)得到过冲响应比a=5.17，进而由前述方法确定传感器的阻尼比ζ=0.686。依据本文所提出评价方法，不难看出该传感器具有较佳的性能。

图9 典型传感器功能实验曲线Fig.9 Functional test curves of the typical accelerometer sensor

5 结语

本文通过SLJ－100型力平衡式加速度传感器，介绍了力平衡式加速度传感器的工作原理及系统动力方程。基于系统动力方程，计算了功能试验响应及频率响应。分析功能试验结果，系统固有频率ωn影响着功能试验去阻尼响应结果。ωn值越大，去阻尼部分响应振荡越剧烈;同时，随着阻尼比值ζ逐渐增加，功能试验响应中有阻尼响应过冲响应会逐渐减小。

由频率响应结果而知，在特定固有频率ωn下，阻尼比值的大小对系统幅频特性及相频特性具有显著影响，ζ的适当选取可以改善仪器的动态响应特性。按照频率响应特性分析，力平衡式加速度传感器阻尼比值选择在0.68～0.70范围内最佳。

综合全文，以功能试验为基础去评价力平衡式加速度传感器的性能可用以下的方法步骤:

(1)从功能试验响应判断传感器的工作状态是否正常;

(2)依据功能试验中的去阻尼响应确定出n个波峰或波谷间的时间t，由式ωn=2π(n－1)/t确定传感器的自振频率，并与传感器固有频率标称值比较，确定系统固有频率是否发生变化;

(3)依据功能试验中的去阻尼响应确定阶跃响应A及过冲响应B，并由式a=×100%计算过冲响应比，并通过内插方法确定出加速度传感器的阻尼比值ζ。

(4)当0.68≤ζ≤0.70，传感器性能最佳。

胡聿贤.2006.地震工程学［M］.北京:地震出版社.

李彩华.2005.力平衡加速度传感器设计分析［J］.传感器技术，24(8):46－48.

李德葆，陆秋海.2004.工程振动试验分析［M］.北京:清华大学出版社.

李海亮.2000.地震计阻尼和自振频率的频域测定［J］.地震地磁观测与研究，21(2):7－12.

李科杰.2002.新编传感器技术手册［M］.北京:国防工业出版社.

曲家骐，王季秩.1998.伺服控制系统中的传感器［M］.北京:机械工业出版社.