量子系统中纯态和混合态量子芝诺效应研究

孙权海，潘国柱，吴诗芬，李凌峰

（1.安徽三联学院 基础实验教学中心，安徽 合肥 230601；2.皖西学院 材料与化工学院，安徽 六安 237012）

0 引言

量子信息是由量子力学和信息科学相结合而发展起来的新兴学科，主要由量子通信和量子计算两部分组成［1-2］.量子信息因其独特的优越性而受到人们普遍的关注.其中量子通信由于具有较高的实际应用价值，在量子信息中占有极其重要的地位.近年来,量子芝诺效应在量子通信中的应用研究引起人们极大的兴趣，同时在此领域中的应用已经取得了实质性的进展，发挥着比较重要的作用［1-8］.

量子芝诺效应即是对一个不稳定量子系统频繁的测量可以冻结该系统的初始状态或者阻止系统的演化［9-12］.如果测量时间间隔足够短，可以把测量看作是连续的测量，正是由于这样的测量所引起的波函数坍缩阻止了量子态之间的跃迁.然而人们对量子芝诺效应的研究大多数只是考虑初始态为纯态的情形.纯态不稳定系统的量子芝诺效应的存在性已经被证实［11-12］.此外，孙等［13］已提出系统的初始状态对量子芝诺效应的发生有一定的影响.至今为止，有关初始态为混合态的量子芝诺效应罕见报道.众所周知，大多数量子系统由于与环境相互作用而不可避免地处于混合态.因此研究初始时刻处于混合态的不稳定系统的量子芝诺效应将比仅仅考虑纯态的量子芝诺效应更加具有实际意义.故此，对混合态系统的量子芝诺效应的研究将是本文的主要内容，此研究将为量子芝诺效应的应用提供必要的理论储备和基础知识.

1 量子芝诺效应及其基本原理

以一个简单的两能级原子量子系统为例，研究该系统在被频繁的投影测量情况下是如何产生量子芝诺效应的.两能级系统具有离散的本征态，这里我们选择其本征态作为测量基，也就是说测量基就是两能级量子系统的两个本征态之一.此外，系统的初始状态也处于两个本征态之一，然后再执行频繁和重复的投影测量.假设两能级系统在相干拉比振荡下的哈密顿量为：

则在τ时刻对应的时间演化算符为：

在总时间为t测量相隔时间为τ的n次投影测量后，系统初始状态的存活概率为：

上式结果已忽略了高阶小项，显然当n→∞时，P(t)→1，因而式（3）可以表明量子芝诺效应的发生.

总之，我们对具有离散本征态的不稳定量子系统进行简单和频繁的投影测量，就可以使系统状态失去动态演化的机会，这正是量子芝诺效应现象的发生.

2 复合量子系统中混合态量子芝诺效应

下面我们来研究两体量子系统中混合态量子芝诺效应.频繁地对两体联合纠缠纯态系统进行投影测量将导致子系统量子芝诺效应的发生，而我们所感兴趣的子系统的初始状态却处于混合态.我们考虑一个由子系统A和B组成的两体复合量子系统，制备其初始状态为纠缠纯态，研究其中一个子系统初始状态的存活概率.分析所得结果并尝试获得与量子芝诺效应有关的具有实际意义的结论.总之，我们主要解决的问题是：所要考察的初始态为混合态的不稳定系统（例如子系统A）是如何产生量子芝诺效应的.如上所述，我们选择两个两能级原子A和B组成一个复合系统，制备此复合系统初始状态如下：

其中

简单起见，这里的α和β均为实参数，且满足关系式α2+β2=1.当然，复合系统的初始态是一个纠缠纯态.现在只考察子系统A的状态，可通过对子系统B状态求迹（trace）得到子系统A状态的密度算符：

至此我们可以明显地看出子系统A的初始状态其实是一混合态.假设在相互作用绘景中该复合系统的哈密顿量为：

为了使计算过程简单化并且不影响最后结论的前提下，我们可以取ϖ1=ϖ2=ϖ.相应地，复合系统的时间演化算符为：

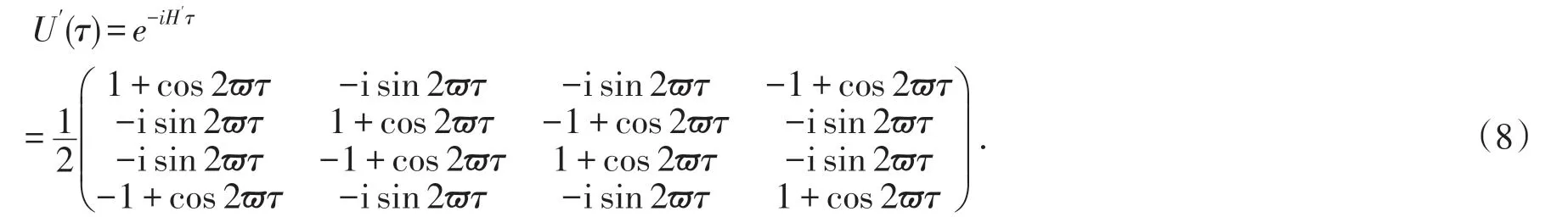
现在我们对整个复合系统执行n次投影测量，而且每次操作都使用相同的投影算符ψ0ABψ0.换言之，在每个时间间隔τ结束的瞬间我们都要将整个系统投影到其初始状态上.完成n次投影测量后，经历t时间后子系统A初始状态的存活概率为：

在式（9）最后一步计算中，忽略了高阶小项.然而我们关注的是子系统A的演化情况而不是整个系统的演化.显然完成上述操作后子系统A的初始混合态的存活概率是接近于1的，并且随着测量次数n的增大初始态存活概率也是增大的.总之，这种现象恰恰反映了量子系统中混合态量子芝诺效应的存在.

3 结论

综上所述，通过执行频繁的投影测量可以阻止纯态和混合态量子系统的演化.换言之，频繁的测量可以使不同状态的量子系统保持稳定.值得关注的是，处于式（4）状态的复合量子系统，尽管该系统的初始态是一个纯态，但是对于任意一个子系统来说其初始态却是混合态.总之，当我们对此系统进行频繁的测量时，混合初始态的量子芝诺效应就会发生.这样的结果给我们带来了极大的惊喜，同时希望此结论为未来量子芝诺效应的相关研究提供有价值的理论基础.

在传统的量子芝诺效应解释中，投影测量或者波包塌缩是必不可少的前提，但是最近人们研究发现，投影测量并不是量子芝诺效应发生的必需条件，它完全可以被一个幺正测量动力学过程所取代，这就使得芝诺动力学过程不再是非幺正的.因此，量子芝诺效应并不依赖于非幺正的投影测量和波包塌缩，而是可以利用系统与外部自由度的连续或者分离耦合，这就使得量子芝诺效应可以只依赖于幺正的耦合演化［13］.上述量子芝诺效应的幺正解释将为其在量子信息中找到更广泛的应用奠定了理论基础，也使其在实验中更容易实现.

［1］NIELSEN M A，CHUANG I L.Quantum computation and quantum information［M］.Cambridge：Cambridge University Press，2000：1-5.

［2］张永德.量子信息物理原理［M］.北京：科学出版社，2006：2-4.

［3］YANG Y P，XU J P，CHEN H，et al.Long-lived entanglement between two distant atoms via left-handed materials［J］.Phys Rev A，2010，82：030304-030308.

［4］ZHENG S B，GUO G C.Efficient scheme for two-atom entanglement and quantum information processing in cavity QED［J］.Phys Rev Lett，2000，85：2392-2395.

［5］RAO D D，KURIZKI G.From Zeno to anti-Zeno regime：Decoherence-control dependence on the quantum statis⁃tics of the bath［J］.Phys Rev A，2011，83：032105-032111.

［6］XU D Z，AI Q，SUN C P.Dispersive-coupling-based quantum Zeno effect in a cavity-QED system［J］.Phys Rev A，2011，83：022107-022112.

［7］NAKAZATO H，TAKAZAWA T，YUASA K.Purification through Zeno-like measurements［J］.Phys Rev Lett，2003，90：060401-060405.

［8］QIU NAN，WANG S C，KWEK L C，et al.Preparation and entanglement purification through two-step measurements［J］.Phys Rev A，2012，86：012313-012320.

［9］MISRA B，SUDARSHAN E C G.The Zeno’s paradox in quantum theory［J］.J Math Phys，1977，18：756-763.

［10］ITANO W M，HEINZEN D J，BOLLINGER J J，et al.Quantum Zeno effect［J］.Phys Rev A，1990，41：2295-2300.

［11］FRERICHS V，SCHENZLE A.Quantum Zeno effect without collapse of the wave packet［J］.Phys Rev A，1991，44：1962-1968.

［12］张永德，潘建伟.量子芝诺效应新论［J］.今日物理，1995，14：7-9.

［13］AI Q，LI Y，ZHENG H，et al.Quantum anti-zeno effect without rotating wave approximation［J］.Phys Rev A，2010，81：042116-042128.