多维时间序列Granger因果图Markov性

魏岳嵩

（淮北师范大学 数学科学学院，安徽 淮北 235000 ）

1 引言

自从1969年Granger［1］提出Granger因果性概念以来，Granger因果性已成为衡量系统变量间动态关系的重要依据，在金融经济、信号处理、神经网络、医学等［2-5］众多领域都有着广泛的应用.Granger指出：如果在其余变量信息给定的情况下，融入某一变量的信息有助于对另一变量将来值的预测，则该变量是另一变量的原因.当前对系统变量间Granger因果关系的研究多采用两变量Granger因果性检验法［6-7］，由于经常忽视其他重要解释变量所产生的影响，常会导致伪因果关系的出现.此外，两变量Granger因果性检验只能检验两变量间长期的因果关系，却无法度量变量间的即时因果关系，这些都限制了该检验方法的使用范围.

近年来，作为分析和处理多元数据重要工具的图模型方法已经被广泛用于时间序列问题的研究.利用图模型方法研究时间序列变量之间的Granger因果性，能够直观地呈现变量间的多种因果关系，同时也可检验多个变量间的Granger 因果关系.Eichler［8］首先利用图模型方法研究变量间的因果关系，建立了Granger 因果图，并在Granger 因果图中融入变量间的即时因果关系.魏岳嵩等［9］则讨论了Granger 因果图结构的辨识问题，提出了Granger因果图的条件互信息辨识方法.在此基础上，本文进一步讨论Granger因果图的相关性质.

2 多维时间序列Granger因果图

令V是一非空有限集，图G=(V,E)是一有序集，其中V中的元素称为图的顶点，而E={(a,b)|a,b∈V}中的元素称为边.一条边(a,b)称为图G中的无向边，若(a,b)∈E并且(b,a)∈E,在图中用a-b表示，此时称a和b为邻居.a的邻居集记为ne(a).一条边 (a,b)称为图G中的有向边，如果 (a,b)∈E但 (b,a)∉E,在图中用a→b表示，此时称a为b的父亲，b为a的孩子.a的父亲集记为pa(a)，a的孩子集记为ch(a).若图G中既有有向边又有无向边，则称其为混合图.长度为n的从a到b的路径是指由不同顶点组成的从a到b的序列 {a=i0,i1,…,in=b}，满足对所有的k=1,2,…,n都有 (ik-1,ik)∈E.如果对于所有的k=1,2,…,n都有(ik-1,ik)∈E但(ik,ik-1)∉E，则称该路径为有向路径.若在图G中存在由a到b的有向路径，则称a是b的祖先，b是a的后代.a的所有祖先组成的集合称为a的祖先集，记为an(a).

如果A⊆V,EA⊆E，则称图GA=(A,EA)为图G=(V,E)的子图.如果EA=E⋂(A×A)，则称GA是由A导出的G的子图.此外，用分别表示集合A的父亲集、孩子集和邻居集.

设X(t)=(X1(t),X2(t),…,Xk(t))T是定义在概率空间(Ω,F,P)上的k维随机过程，V={1,2,…,k}为相应的指标集.对任意A⊂V，以XA={Xa,a∈A}表示XV=X(t)的多变量子过程，以X(t)={X(s),s＜t}表示在时刻t之前该随机过程的信息集，以G=(V,Ed,Eu)表示顶点集为V的混合图，其中Ed⊆{(u,v)∈V×V|u≠v}为有向边集，而Eu⊆{(u,v)∈V×V|u≠v}为无向边集.

假设序列X(t)满足以下条件：

（C1）X(t)=(X1(t),X2(t),…,Xk(t))T是概率空间(Ω,F,P)上的平稳随机过程.

（C2）序列中所有变量都是可观测的，即满足因果充分性条件.

（C3）所有变量的联合分布关于某一乘积测度是绝对连续的，并且具有正的连续概率密度.

定义1（Granger因果性）设A和B是V的不相交子集，XA和XB是XV的相应子过程，XV(t)表示在时刻t的所有有关V的信息集.

（2）如果XB(t)⊥XA(t)|{XV(t),XV{A,B}(t)}，则称XA和XB关于XV(t)是非同期因果的，记为XA≁XB[XV].

定义2（Granger因果图）设X(t)=(X1(t),X2(t),…,Xk(t))T是定义在概率空间(Ω,F,P)上的k维平稳随机过程，如果以下条件成立，则以{X(t)}各分量为顶点集V={1,2,…,k}的混合图G=(V,Ed,Eu)称为Granger因果图.

（1）对任意i,j∈V且i≠j有

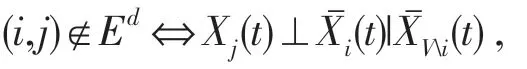
（2）对任意i,j∈V且i≠j有

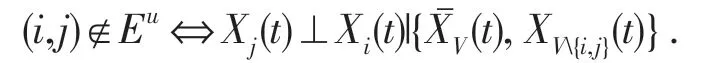
3 Granger因果图的Markov性

设G=(V,E)是Granger因果图，a和b是G中的两个顶点，π=(e1,e2,…,en)是a和b之间的一条路径，其中a=i0,i1,…,in=b.若路径 π 包含结构 →ik←, -ik←, →ik-之一，则称点ik是路径π 上的p-对冲点，否则称ik是路径π 上的非p-对冲点.如果路径π 中所有的中间点都为对冲点，则该路径为完全对冲路径.设C⊆V{a,b}，如果条件（1）{ik|ik是π上的非p-对冲点}⋂C≠ϕ和条件（2）{ik|ik是π上的p-对冲点}⊄⋂C≠ϕ至少有一个成立，则称在图G中路径 π 被C阻断，否则称在给定C的条件下路径π 在图G中连通.如果在图G中a和b之间的所有路径都被C阻断，则称在图G中C p-分离a和b，否则称C p-连通a和b.设A,B和C是V中两两互不相交子集，其中A和B非空，若对任意a∈A和b∈B，在G中C p- 分离a和b，则称C在G中p- 分离A和B.

定义3（Granger 因果图Markov 性）设G=(V,E)是时间序列Granger 因果图，如果对于所有a，b∈V,a≠b有a→b∉E⇒Xa■Xb[XV]及a-b∉E⇒Xa≁Xb[XV]，则称图G满足成对Granger因果Markov 性，记为 PGCM.如果对于所有a∈V有，则称G满足局部Granger 因果Markov 性，记为LGCM.如果对于V的所有子集A有G满足块递归Granger因果Markov性，记为BGCM.

定理1设G=(V,E)是Granger 因果图，A，B和C是V中两两互不相交子集，且V=A⋃B⋃C（其中A和B非空），则A和B被C分离当且仅当A中任意点a和B中任意点b之间不存在完全对冲路径.

证明（必要性）假设点a∈A和b∈B，π=(e1,e2,…,en)是G中a和b之间的一条完全对冲路径，且a=i0,i1,…,in=b.为简单起见，不妨设该路径是A和B之间所有完全对冲路径中的最短路径，则对所有的k∈{1,2,…,n-1}，都有ik∈C，否则，若存在r∈{1,2,…,n-1}，使得ir∈A（或者ir∈B），则此时(er+1,er+2,…,en)（或者(e1,e2,…,er)）是A和B之间一条比 π 更短的完全对冲路径，矛盾.由于路径 π 是完全对冲路径，因此路径中的所有中间点都为对冲点，从而该路径在给定C的条件下是连通路径，这和已知条件矛盾，因此A中任意点a和B中任意点b之间不存在完全对冲路径.

（充分性）已知A中任意点a和B中任意点b之间不存在完全对冲路径，假设A和B不被C分离，则存在a1∈A和b1∈B，以及a1和b1之间的一条关于C连通的路径π=(e1,e2,…,en).不妨设该路径是A和B之间所有连通路径中的一条最短路径，则对所有的k∈{1,2,…,n-1}，都有ik∈C.否则，存在r∈{1,2,…,n-1}使得ir∈A（或者ir∈B），此时 (er+1,er+2,…,en)（或者 (e1,e2,…,er)）是A和B之间一条比 π更短的连通路径，矛盾.由于路径π 关于C是连通的，且所有的中间点都属于C，因此所有的中间点都为对冲点，从而π 是完全对冲路径，和已知矛盾，因此A和B被C分离.

定理2设G=(V,E)是Granger 因果图，A和B是V的两个互不相交子集，则A和B被V{A,B}分离当且仅当 (A⋃ ch(A))⋂(B⋃ch(B))=ϕ且ne(A⋃ch(A))⋂(B⋃ ch(B))=ϕ.

证明（必要性）已知A和B被V{A,B}分离，如果(A⋃ch(A))⋂(B⋃ch(B))≠ϕ，则存在i∈(A⋃ch(A))且i∈(B⋃ch(B)).当i∈A时，由于A和B互不相交，此时必有i∈ch(B)，从而A和B不能被V{A,B}分离；当i∈ ch(A)且i∈B时，显然A和B不能被V{A,B}分离；当i∈ ch(A)且i∈ch(B)时，必存在a∈A和b∈B使得a→i←b，此 时A和B也 不 能 被V{A,B} 分 离.综 上 可 知 (A⋃ch(A))⋂(B⋃ch(B))=ϕ.若ne(A⋃ ch(A))⋂(B⋃ ch(B))≠ϕ，则存在i∈ne(A⋃ch(A))且i∈(B⋃ ch(B))，即存在a∈A使得a-i或者存在a∈A及k∉A使得a→k-i，同时i∈B或者存在b∈B使得b→i成立，显然无论哪种情况，A和B都不能被V{A,B}分离，因此必有ne(A⋃ch(A))⋂(B⋃ch(B))=ϕ.

（充分性）已知 (A⋃ch(A))⋂(B⋃ch(B))=ϕ且ne(A⋃ch(A))⋂(B⋃ ch(B))=ϕ，设A和B不被V{A,B}分离，则存在a∈A和b∈B以及a和b之间的一条路径 π=(e1,e2,…,en)，且该路径关于C是连通的.不妨设该路径是A和B之间所有连通路径中的最短路径，则由定理1知对所有的k∈{1,2,…,n-1}都有ik∈C且π是完全对冲路径，故 π 必是以下4 种形式之一：a→c←b，a→c-b，a-c←b，a→c-d←b，显然有(A⋃ ch(A))⋂(B⋃ ch(B))≠ϕ或者ne(A⋃ ch(A))⋂ (B⋃ ch(B))≠ϕ，矛盾.因此A和B被V{A,B}分离.

定理3设G=(V,E)是Granger 因果图，π=(e1,e2,…,en)是a和b之间的一条路径，其中a=i0,i1,…,in=b，记C={ik|ik是π上的对冲点}，则{i0,i1,…,in}⊆an({a,b}⋃C).

证明当n=1 时结论显然成立.下面考虑n≥2 的情形.以m表示路径π 中对冲点的个数，现对m利用归纳法证明命题结论.

若m=0 即C=ϕ时，路径π只有两种可能形式，即存在r满足0≤r≤n，π 为a=i0←…←ir-1←ir→ir+1→…→in=b，或者存在r满足0≤r≤n，π为a=i0←…←ir-1-ir→ir+1→…→in=b，显然对于两种情况都有{i0,i1,…,in}⊆an({a,b}⋃C).

当m＞ 0 时，设k∈C即k=ir(0＜r＜n)是 π 上的对冲点，则 π1=(e1,e2,…,er)是G中从a到k的路径，π2=(er+1,er+2,…,en)是G中从k到b的路径.令C1={is∈C|0＜s＜r}和C2={is∈C|r＜s＜n}分别是 π1和π2上的对称点集，则两个路径中的对冲点数都少于m个，由归纳假设知{i0,i1,…,ir}⊆an({a,k}⋃C1)及{ir,ir+1,…,in}⊆an({k,b}⋃C2).由于k∈C，因此an({a,k}⋃C1)⊆an({a,b}⋃C)，an({k,b}⋃C2)⊆an({a,b}⋃C)，即{i0,i1,…,in}⊆an({a,b}⋃C).

定理4设G=(V,E)是Granger 因果图,a和b是G中的两个顶点，C⊆V{a,b}，则C在图G中p- 分离a和b当且仅当C在图Gan(a⋃b⋃C)中p- 分离a和b.

证明（必要性）假设在图Gan(a⋃b⋃C)中，在给定C的条件下，a和b之间存在连通路径 π.由于Gan(a⋃b⋃C)⊆G，故 π 也是G中相对于条件集C的连通路径，矛盾.因此C在图Gan(a⋃b⋃C)中p- 分离a和b.

（充分性）假设π=(e1,e2,…,en)是图G中a和b之间关于C的连通路径，令D是π 上的对冲点集，则由定理 3 知 π 也是图Gan(a⋃b⋃D)中的一条路径.由于D⊆an(C)，故Gan(a⋃b⋃D)⊆Gan(a⋃b⋃C)，从而 π 也是图Gan(a⋃b⋃C)中关于C的连通路径，矛盾.即C在图G中p- 分离a和b.

推论1设G=(V,E)是Granger因果图，A,B和C是V中两两互不相交子集，其中A和B非空，则C在图G中p- 分离A和B当且仅当C在图Gan(A⋃B⋃C)中p- 分离A和B.

定理5设X(t)=(X1(t),X2(t),…,Xk(t))T,t∈Z是n维平稳随机过程，G=(V,E)是相应的时间序列Granger因果图，A，B和C是V中两两互不相交子集，且V=A⋃B⋃C，则BGCM⇔LGCM⇔PGCM.

证明由［10］定理3.1知，当X(t)满足条件（C3）时有

由［8］引理A.2知，BGCM⇔LGCM⇔PGCM.

［1］GRANGER C.Investigating causal relations by econometric models and cross-spectral methods［J］.Econometrica，1969，37：424-438.

［2］KAMINSKI M，DING Z，TRUCCOLO W，et al.Evaluating causal relations in neural systems：Granger causality，directed transfer function and statistical assessment of significance［J］.Biological Cybernetics，2001，85：145-157.

［3］KONYA L.Exports and growth：Granger causality analysis on OECD countries with a panel approach［J］.Economic Model⁃ling，2006，23（6）：978-992.

［4］NAGARAJAN R，UPRETI M.Comment on causality and pathway search in microarray time series experiment［J］.Bioinfor⁃matics，2008，24（7）：1029-1032.

［5］郭水霞.频域格兰杰因果关系及其在信号处理中的应用［J］.计算机工程与应用，2008，44（3）：5-9.

［6］MUKHOPADHYAY N，CHATTERJEE S.Causality and pathway search in microarray time series experiment［J］.Bioinfor⁃matics，2007，23：442-449.

［7］FIEUWS S，VERBEKE G，MOLENBERGHS G.Random-effects models for multivariate repeated measures［J］.Statistical Methods in Medical Research，2007，16（5）：387-397.

［8］EICHLER M.Granger causality and path diagrams for multivariate time series［J］.Journal of Econometrics，2007，137：334-353.

［9］魏岳嵩，田铮.多维时间序列Granger因果性的一种图模型学习方法［J］.系统科学与数学，2011，31（5）：549-558.

［10］LAURITZEN SL.Graphical models［M］.Oxford：Oxford University Press，1996.