几类图的pebbling数

王艳秋，叶永升

（淮北师范大学 数学科学学院，安徽 淮北 235000）

1 基本概念

连通图的一个pebbling是一些pebble在这个图的顶点上的一种放置方式，一个pebbling移动是从一个顶点上移走两个pebble，扔掉其中的一个而把另一个移到与其相邻的一个顶点上.图G的一个顶点v的pebbling数是最小的数f(G,v)，满足从G的顶点上f(G,v)个pebble的任意一种放置开始，总可以通过一系列的pebbling移动把一个pebble移到顶点v上.图G的pebbling数记为f(G)，是对G的所有顶点v来说f(G,v)的最大值.

对于pebbling 数f(G)已经得到了一些结果（见文献［1-4］），如果除顶点v之外每一个顶点上都只放置一个pebble，则没有一个pebble 能够移到v上，另外，如果顶点w与v的距离为d，且2d-1 个pebble放置在w上，则也不能把一个pebble移到v上，所以有f(G)≥max{|V(G)|, 2d} .这里|V(G)|表示图G的顶点个数，而d为图G的直径.

给定G的一种pebbling，G的一个传送子图是一条路x0,x1,…,xk，使得在顶点x0上至少有2 个pebbles，且除了可能xk外的其他顶点上至少有1个pebble.这时可以把1个pebble从x0传送到xk.

扇图Fn是一条路Pn-1加上另一个顶点，此顶点与路Pn-1的每个顶点都相邻.轮图Wn是一个圈Cn-1再加上与此圈中每个顶点都相邻的一个顶点.

下面我们给出几个图的定义：

定义1设Fn是由顶点v1,v2,…,vn-1的路再加上与此路中的每个顶点都相邻的一个顶点v0，另有路Pk=u1u2…uk，连接v0与uk，便得到Fn∗Pk.

定义2设Wn是由顶点v1,v2,…,vn-1的圈Cn-1再加上与此圈中每个顶点都相邻的一个顶点v0，另有路Pk=u1u2…uk，连接v0与uk便得到Wn∗Pk.

定义3设Wm是由顶点a1,a2,…,am-1的圈Cm-1再加上与此圈中每个顶点都相邻的一个顶点a0，Wn是由顶点b1,b2,…,bn-1的圈Cn-1再加上与此圈中每个顶点都相邻的一个顶点b0，路Pk-1=w1w2…wk-1，分别连接a0与w1，b0与wk-1，便得到Wm∗Pk-1∗Wn，此图被称为双轮图.

文献［2］给出了扇图和轮图的pebbling数，f(Fn)=n和f(Wn)=n.文献［3］给出了偶圈图的pebbling数，f(C2n)=2n.文献［4］证明了完全二部图的pebbling 数，f(Km,n)=m+n.文献［5］给出了f(C2n∗Pm)=2m+n，f(C2n∗Pk-1∗C2m)=2m+n+k，f(Pk∗C2n∗Pm)=2m+n+k.本文研究了图Fn∗Pk，Wn∗Pk和双轮图Wm∗Pk-1∗Wn的pebbling数.

本文考虑的图都是简单无向连通图，设图G的顶点集为V(G)，边集为E(G).给定G的pebble 的一个分配，对G的任意顶点v.p(v)代表v上的pebble的个数.为放置在G的顶点上的pebble 个数.

2 主要结论

在这一部分，首先给出Fn∗Pk的pebbling 数，在此基础上得出Wn∗Pk的pebbling 数，最后研究了Wm∗Pk-1∗Wn的pebbling数.为定理的证明，先给出下面的引理：

引理［1］f(Pn)=2n-1，其中Pn为n个顶点的路.

定理1f(Fn∗Pk)=n+2k+1-2(n≥5,k≥2).

证明如果p(v2)=p(v3)=…=p(vn-1)=1，p(v1)=2k+1-1，那么Fn∗Pk被放置n+2k+1-3 个pebble，可是顶点u1无法得到一个pebble.所以f(Fn∗Pk)≥n+2k+1-2.下面证明f(Fn∗Pk)≤n+2k+1-2.

（1）设p(v0)=0，如果任意vi，p(vi)≥2(i≠0)，则可移动一个pebble 给v0.若p(vi)≤1(i≠0)，则至少有n+2k+1-2-(n-1)=2k+1-1(＞2k)个pebble 放在路u1,u2,…,uk,v0上，由引理知，可以移动一个pebble给v0.

（2）设p(vi)=0(1≤i≤n-1)，不妨设p(v1)=0，如果p(v0)≥2 或p(v2)≥2 或p(vi)≥4(3≤i≤n-1)，则v1均可得到一个pebble.否则，p(v0)≤1且p(v2)≤1且p(vi)≤3(3≤i≤n-1)，此时有以下情形：

（2.1）当p(v0)=1 时，如果 2≤p(vi)≤3，那么{vi,v0,v1} 成传送子图；如果p(vi)≤1，那么至少有n+2k+1-2-(n-2)+1(=2k+1+1)个pebble 放在路u1,u2,…,uk,v0,v1上，由引理可知，可以移动一个pebble给v1.

（2.2）当p(v0)=0 时，如果2≤p(vi)≤3,那么任意两个顶点vi,vj(3≤i,j≤n-1)可分别给v0一个peb⁃ble，v0再给v1一个；如果p(vi)≤1,则至少有n+2k+1-2-(n-2)=2k+1个 pebble 放在路u1,u2,…,uk,v0,v1上，那么可移动一个pebble给v1.

（3）设p(ui0)=0(1≤i0≤k), 记A={u1,u2,…,uk,v0} ,B={v1,v2,…,vn-1} .设p(A)≥p(B)且p(A)-p(B)=p，其中 0≤p≤n+2k+1-2，又由于p(A)+p(B)=n+2k+1-2，可知，n和p同时为奇数或偶数，故有

B至少可以移给v0的pebble个数为，则A中的pebble个数至少为

所以可以移给ui0一个pebble.

如果p(B)＞p(A)且p(B)-p(A)=q(0＜q≤n+2k+1-2)，则n和p同奇同偶，并且若n和q均为偶数，则n+2k+1-2 也为偶数，有以下情形：

当q=n+2k+1-2 时，即把n+2k+1-2 全放在B中，此时p(B)=n+2k+1-2，则B至少可以给顶点v0的pebble个数为，所以A中至少有2k个pebble，可以移给ui0一个pebble.

当 0＜q≤n+2k+1-4，B至少可以给顶点v0的pebble 个数为则移动之后A中的pebble个数至少为

所以可以移给ui0一个pebble.

当n和q均为奇数时，情况与上面类似，ui0也可以得到一个pebble.综上所述，

推论f(Wn∗Pk)=n+2k+1-2(n≥5,k≥2).

证明由于图Fn∗Pk是图Wn∗Pk的生成子图，故f(Wn∗Pk)≤n+2k+1-2.如果p(v2)=p(v3)=…=p(vn-1)=1，p(v1)=2k+1-1，那么Wn∗Pk被放置n+2k+1-3 个pebble，可是顶点u1无法得到一个pebble.所以f(Wn∗Pk)≥n+2k+1-2.因此f(Wn∗Pk)=n+2k+1-2(n≥5,k≥2).

定理2f(Wm∗Pk-1∗Wn)=m+n+2k+2-4(m≥5,n≥5).

证 明如果p(a2)=p(a3)=…=p(am-1)=1，p(b1)=2k+2-1，p(b2)=p(b3)=…=p(bn-1)=1.那么Wm∗Pk-1∗Wn被放置m+n+2k+2-5 个 pebble，顶点a1无法得到pebble，因此f(Wm∗Pk-1∗Wn)≥m+n+2k+2-4.下面我们证明f(Wm∗Pk-1∗Wn)≤m+n+2k+2-4.

首先，设目标顶点为a0，即p(a0)=0.

令A={a1,a2,…,am-1}，B={a0,w1,w2,…,wk-1,b0,b1,…,bn-1} .若对于某个ai(i≠ 0)，有p(ai)≥2，则a0可得一个pebble.若对于所有的ai(i≠ 0)，p(ai)≤1，则至少有

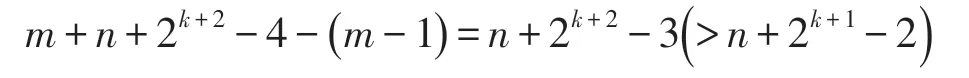
个pebble放在B中，由推论可知，a0可得一个pebble.

其次，设目标顶点为ai(i≠0)，不失一般性，设p(a1)=0.若p(a0)≥2 或p(ai)≥4(i≠ 0,1,2,m-1)或p(a2)≥2 或p(am-1)≥2.则{a0,a1} 或{ai,a0,a1} 或{a2,a1} 或{am-1,a1} 成传送子图，a1可得一个pebble.否则，p(a0)≤1且p(ai)≤3(i≠ 0,1,2,m-1)且p(a2)≤1且p(am-1)≤1，我们有以下情形：

（1）当p(a0)=1 时，如果p(ai)≥2，则{ai,a0,a1} 成传送子图，可移给a1一个pebble；如果p(ai)≤1，则至少有

个pebble放在B中，则a0可以得到一个pebble，之后a0可以给a1一个.

（2）当p(a0)=0 时，如果p(ai)≥2，则任意两个顶点ai,aj(i,j≠0,1,2,m-1)可分别给a0一个pebble，a0得到两个pebble后可给a1一个；如果p(ai)≤1，则至少有m+n+2k+2-4-(m-2)=n+2k+2-2 个pebble放在B中，此时令C={a0,w1,w2,…,wk-1,b0}，D={b1,b2,…,bn-1} .

设p(C)≥p(D)且p(C)-p(D)=s(0≤s≤n+2k+2-2)，由于p(C)+p(D)=n+2k+2-2，可以知道,n和s同时为奇数或偶数.所以有D至少可以移给b的pebble0个数为则移动之后C中的pebble个数至少为

所以可以移给a0两个pebble，那么a1可以从a0处得到一个pebble.

设p(C)＜p(D)且p(C)-p(D)=t(0≤t≤n+2k+2-2)，同样，n和t亦同奇同偶,并且

若n和t同为偶数，则n+2k+2-2 为偶数.

当t=n+2k+2-2 时，即n+2k+2-2 个pebble全部放在D中，此时D至少可移给b0的pebble个数为

则可移给a0两个pebble，那么a1可以从a0处得到一个pebble.

当 0≤t≤n+2k+2-4 时，D至少可以移给b0的 pebble 个数为则移动之后C中的pebble个数至少为

所以可移给a0两个pebble，那么a1可以从a0处得到一个pebble.

若n和t同为偶数，情况与此类似.

最后，设目标顶点为wi(1≤i≤k-1)，不失一般性，设为wi0,即p(wi0)=0.令

由推论知，f(A′)=m+2i0+1-2，f(B′)=n+2k-i0+1-2.由于f(A′)+f(B′)≤m+n+2k+2-4，所以必有p(A′)≥f(A′)或p(B′)≥f(B′)，因此，wi0总会得到一个pebble.

综上，f(Wm∗Pk-1∗Wn)=m+n+2k+2-4(m≥5,n≥5).

［1］CHUNG F R K.Pebbling in hypercubes［J］.SIAMJ Discrete Math，1989，2（4）：467-472.

［2］FENG R Q，KIM J Y.Pebbling numbers of some graphs［J］.Science in China（Series A），2002,45（4）：470-478.

［3］PACHTER L，SNEVILY S，VOXMAN B.On pebbling graphs［J］.Congr Numer，1995，107：65-80.

［4］冯荣权，金珠英.完全二部图乘积上的Graham pebbling猜想［J］.中国数学（A辑），2001，31（3）：199-203.

［5］高泽图，尹建华.几类二部图的pebbling数［J］.高校应用数学学报，2010，25（3）：365-371.