立体视觉中三维定位误差分析的教学研讨

李晓峰，王蒙蒙，周 宁，陈如通

(电子科技大学通信与信息工程学院，四川成都611731)

立体视觉是由多幅图像(一般两幅)获取物体三维信息的方法[1]。物体表面的每一点对于成像面都有一条投射光线，而这条直线上的每个点在图像上都有相同的二维投影坐标。若已知两幅从不同角度对同一物体拍摄得到的图像，则物体在这两个成像面上的投影光线将在空中相交于一点，这一点的值即可视为被测物体的三维坐标[2]。由于可以直接获得物体的空间位置，立体视觉是人类利用双眼获取环境三维信息的主要途径。随着计算机视觉理论的发展，它在工业测量中发挥的作用越来越重要，具有广泛的应用性[3]。所以对立体视觉的研究是十分有意义的，而且其中所涉及的数学运算较为基本，是本科生“数字图像处理”与“综合课程设计”等课程的教学内容。立体视觉教学涉及的直观有趣的实验可以锻炼学生的创新与实践能力，是一个很好的教学模型。

本文基于摄像机成像的针孔模型，以参考文献[4]为例，通过对比的方式帮助学生分析三维定位的误差处理，促进学生创新意识与实践素质的提高。

1 三维定位误差的分析方法

在立体视觉三维测量中一般采用针孔模型来描述摄像机成像模型[5]。根据已知的一组空间点的三维坐标及其对应的图像平面上投影得到的二维坐标来确定摄像机成像模型参数。但传感器分辨率限制与量化误差等原因造成检测到的目标点与其真实位置之间存在误差。

立体相机的设置如图1所示。典型情况是两台摄像机放在高度相等、光轴平行的位置上，左右成像平面的图像坐标系中原点为(I0，J0)。dv，du分别为两成像平面的水平和垂直像素尺寸，在常见的情况下有dv=du。空间中某点S(x，y，z)在左右图像平面上的投影点分别为(Il，Jl)，(Ir，Jr)。

图1 立体相机设置

假设两相机的焦距都用f表示，基线距离为Δ，由三角几何原理容易得到的坐标为

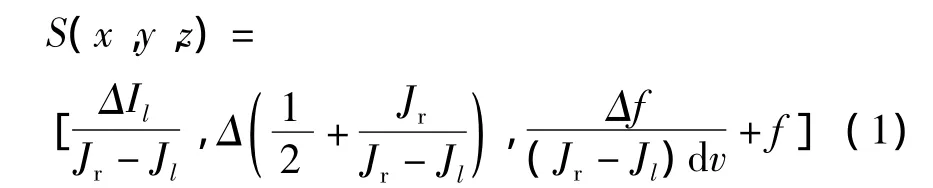
实际上数字图像的坐标只取整数，成像过程中引入量化误差。因此，上式中(Il，Jl)和(Ir，Jr)应该更换为两个实数，它们位于(Il±1/2，Jl±1/2)与(Ir±1/2，Jr±1/2)区间。分析中重点关注的是y－z坐标，它们对应于目标的纵深与水平位置。准确的描述为

其中，nl和nr为0到1之间的小数部分，其意义在本节末表述。

从公式(1)中可以看出，S点的y、z坐标仅是J的函数，而与I相互独立。因此，可以仅通过y－z水平切面来分析目标点的y、z分量。为了分析量化误差，可以考虑左右平面上的一个像素通过交汇所对应的微小目标区域，如图2所示。这个区域(四边形P1P2P3P4)就是量化造成的不定区域(ROU)，也就是误差区域。

图2 立体空间中目标点的量化误差区域

为了分析量化误差，相关参考文献[4]研究了nl，nr概率特性。左图像像素L－L+内任取一点对应于ROU中线段 的投影;再划分为微元，它在右图像像素 R－，R+间投影为微分 δnr。参考文献基于几何关系通过计算线段长度|P5－P6|与|P7－P8|求解边缘概率密度，最终得出nl，nr的联合分布概率密度:

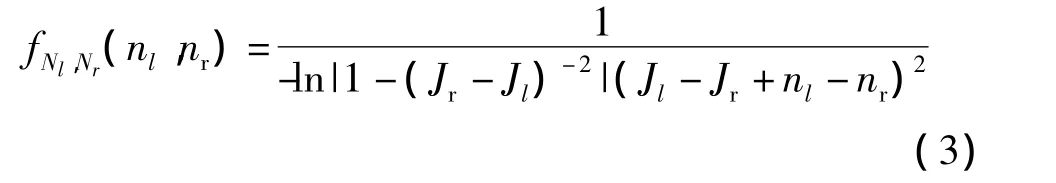
式中，nl，nr正是量化舍弃的部分。

2 参考文章中误差分析的改进

参考文章[4]是一篇经典文献，它对三维定位误差的分析并不深奥，但是过程相当繁琐，学生阅读时常常感到过于繁杂而不能深入理解。例如，在以立体视觉定位实验作为项目的“综合课程设计”中，学生首先学习有关的基本原理，而后通过实验拍摄多组图像，分别计算各个目标的位置，最后分析定位误差。实验中该文章被用做参考文献，但教学实践发现，大多数学生阅读此文献非常困难，教学效果很差。分析其主要原因在于其中的推导繁琐且篇幅很长。其实，学生已学知识本身已经可以方便地解决这个看似复杂的问题。由此我们提出利用概率论和随机信号分析中的标准方法完成这一分析的方案。

首先，由成像公式(2)可以看出 y，z为 nl，nr的函数，根据概率论可得到

其中，|J|为雅可比行列式[6]:

考虑ROU为均匀分布区域，则f(y，z)是ROU的面积的倒数，进而可得

将这一方案用于教学实践后发现，因为都是学过的知识，学生容易理解。特别是通过运用已学知识有效地解决这种国际一流学术期刊中的问题，对学生探究问题是很大的鼓舞。他们普遍反映这种方法既提高了融会贯通的能力，又增强了探究问题的信心，因而很有收获。

教学实施中其实还遇到一个新的问题，这种方法得到的nl，nr联合分布密度结果与文献所述的有所不同，而且反复检查理论推导并没有发现问题。这时，正是指导学生通过实验验证分析的良好时机。

3 仿真实验

在比较上述这两个结论时，它们的差异在许多地方并不很突出，只是在特殊点的地方差异明显。因此，实验过程中学生需要有意地选取特殊点来突出与简化问题。

本实验中设定两摄像机基线距离Δ=50mm，摄像机焦距 f=25mm，像素尺寸 dv=12.9μm[7]。选择某对像素Jl，Jr，在相应的ROU区域产生3百万个随机点，它们在左右像平面上成像在这对像素周围，统计这对像素量化区间内20×20的三维直方图，记下它们 50 次的平均值为 m1，1，m1，2，…，m20，20，而式(3)和式(5)的理论值分别记为 P1，1，P1，2，…，P20，20和 q1，1，q1，2，…，q20，20。图 3 给出了两公式理论值与统计值相差的一个例子(这里Jl=10，Jr=-3，单位:像素)。

图3 理论值与统计值的差值统计

由图3可以看出，参考文献[4]的公式(3)比我们推导的公式(5)误差大很多。更好的分析是对数据进行归一化整理[8]。表1为当Jl，Jr选取不同数值时两种方法得到的归一化误差的比较，其中δ1，δ2分别为式(3)和式(5)的归一化误差:

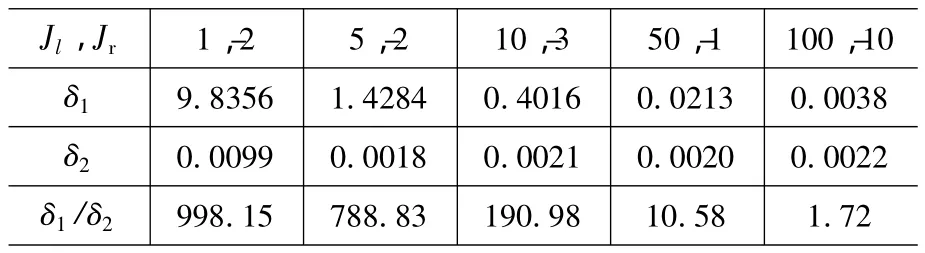
表1 Jl，Jr选取不同数值时归一化误差比较

可以清楚地看出，δ2明显优于δ1。当Jl和Jr选取不同数值时，δ1的波动较大，δ2则趋于平稳。且|Jl|，|Jr|越小，μ = δ1/δ2越大。进行更为充分的实验后，可以得出结论:利用雅可比行列式计算的式(5)才符合实验数据，我们的结论是正确的。

4 结语

本文简要阐述了立体视觉中三维定位误差分析的过程，对比于参考文章提出了更简单的误差处理方法，有效地将复杂的计算过程简单化并得到正确的结果。此方法简单直观，学生容易接受。同时我们还利用Matlab仿真实验，指导学生通过实验对比解决疑惑，让学生在对比分析中理解和掌握相关的数据处理方法。

[1]马颂德，张正友.计算机视觉[M].北京:科学出版社，1998:72-75.

[2]王彦霞，王震洲，刘教民.基于双目立体视觉的三维重建算法[J].石家庄:河北科技大学学报，2008，29(3):219-222.

[3]尚 倩等.基于双目视觉的关键点的检测方法及定位研究[J].北京:计算机测量与控制，2011，19(7):1565-1568.

[4]STEVEN D.BLOSTEIN，THOMAS S.HUANG.Error Analysis in Stereo Determination of 3-D Point Positions[J].IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE，1987，9(6):752-765.

[5]高俊钗，雷志勇，王泽民.高精度测量的相机标定[J].洛阳:电光与控制，2011，18(2):93-95.

[6]李晓峰，李在铭，周宁等.随机信号分析[M].北京:电子工业出版社，2007:12-14.

[7]JiandanChen，SiamakKhatibi，WlodekKulesza.Depth Reconstruction Uncertainty Analysis and Improvement-The DitheringApproach[J].Image and Vision Computing，2010，28:1377-1385.

[8]费业泰.误差理论与数据处理[M].北京:机械工业出版社，2000:118-133.