抛物线形断面最优水力参数及方程指数计算方法

2014-07-02张丽伟

水利水电科技进展 2014年5期

关键词：明渠水深抛物线

张丽伟,滕凯

(1.齐齐哈尔市河道管理处,黑龙江齐齐哈尔 161006;2.齐齐哈尔市水务局,黑龙江齐齐哈尔 161006)

抛物线形断面最优水力参数及方程指数计算方法

张丽伟1,滕凯2

(1.齐齐哈尔市河道管理处,黑龙江齐齐哈尔 161006;2.齐齐哈尔市水务局,黑龙江齐齐哈尔 161006)

针对目前抛物线形断面最优水力参数及抛物线方程指数计算尚没有比较系统研究成果的问题,通过对该种断面均匀流方程的变形整理及近似积分计算,得到了抛物线方程指数一定情况下明渠过水断面最优水力参数的简化计算公式,并通过对简化公式的进一步分析整理,给出了当渠道其他参数(流量、比降及糙率)一定情况下抛物线形断面的最优方程指数为3.35。精度分析及算例计算结果表明:最优水力参数的提出将为该类断面的进一步优化设计提供可靠依据;最优抛物线形断面比其他水力最优断面经济指标更好。

抛物线形渠道;明渠均匀流;水力最优断面;水力参数

随着水利机械化施工技术及工艺的不断提高,抛物线形断面渠道在水利水电灌排水及城市供排水工程中的应用越来越广泛,因此,开展该种断面最优水力参数的研究具有重要意义。通过对均匀流方程的变形整理,魏文礼等[1]给出了半立方抛物线(抛物线方程指数n=3/2)形断面的最优水力参数为a2/3h1/3=0.99078(a为抛物线形断面形状参数;h为断面过水水深),张志昌等[2]给出了抛物线(n= 2.0)形断面的最优水力参数为ah=0.946 73,并认为抛物线形断面是仅次于U形断面的水力最佳断面。这些研究成果为有效优化这两种抛物线形断面的设计奠定了良好的基础。在实际工程中,由于抛物线方程指数n的选取受工程所处地形、地质及过流条件的制约,n可能是大于1的任意数值[3-7],仅给出这两种特殊抛物线方程指数形式过水断面的最优水力参数尚不能满足实际工程的设计要求。因此,研究并提出抛物线方程指数n取大于1的任意数值时的最优水力参数和当渠道其他参数(流量、比降及糙率)一定情况下抛物线形断面的最优方程指数,对进一步开展抛物线形断面渠道优化设计、有效降低工程投资具有重要意义。

由于当n＞1时的正常水深计算涉及不可积分函数,且为超越方程,本文利用二次抛物线近似积分法完成了不可积函数的积分计算,进而完成了n＞1情况下抛物线形渠道断面的最优水力参数计算,并给出了抛物线形断面的最优方程指数n=3.35,经与n=1.5、2.0、4.0及6.0时的最优水力参数断面比较表明,最优方程指数抛物线断面湿周最小,相应的护砌长度最短,断面面积也最小,具有较好的工程实用意义。

1 抛物线形断面均匀流计算公式

以曼宁公式表示的明渠均匀流方程[8]为

式中:n′为渠床糙率;Q为过水流量,m3/s;i为渠底坡降;A为过水断面面积,m2;χ为过水湿周,m。

抛物线形断面曲线方程为

其过水断面面积及湿周分别为

式中B为过水断面水面宽度的1/2,m。

在式(4)中,仅当抛物线方程指数n为个别值(如n=1.5、2.0)时函数可以完成积分,通常情况下均无法通过常规方法完成积分。为此,采用二次抛物线近似法[9]完成对式(4)的积分,其计算公式为

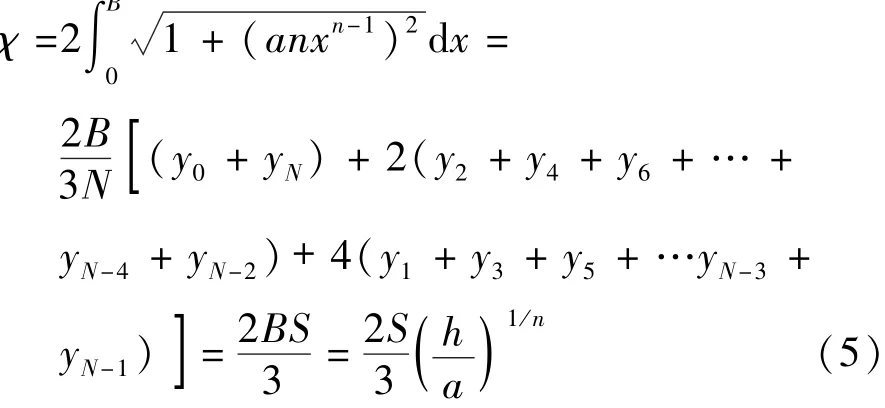
其中

式中:N为在函数自变量x积分区间[0,B]内平均等分的份数,N为偶数;S为无量纲湿周;yi为取第j个等分点时被积分函数的计算值。

在式(3)、式(5)中,设

将式(3)(5)(8)(9)代入式(1)经进一步整理可得

式中:k为已知综合参数;z为中间变量,即抛物线形断面水力参数。

利用式(10)进行抛物线形明渠断面设计需通过试算法完成:设定N值,选取不同的z(值因B=,故B值可求),即可由式(5)完成积分的近似计算。为提高计算精度,在N取值时,将N的每次增幅取为6,并将上一次与本次χ计算值的相对误差小于0.001%时作为N的最终取值,进而求得S。将S及k值代入式(10)即可求得z,当该计算与选定值相等时即为所求值,进而可由式(11)求得渠道的正常水深h0:

2 抛物线形断面最优水力参数

当渠道的过水断面面积A一定、湿周χ最小时,渠道通过的流量Q最大。为此,对式(3)和式(5)求关于h的导数,并令其为零,即

其中

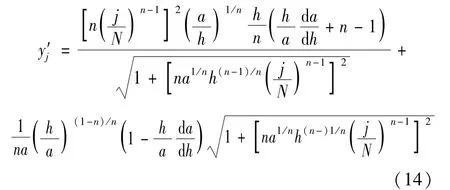
由式(12)整理可得

将式(15)代入式(14),并考虑a1/nh(n-1)/n= aBn-1=z,经整理可得

将式(16)代入式(13)整理可得含最优水力参数z的超越方程。因N值可根据精度要求按前述方法确定,选取不同的抛物线方程指数n,即可由式(13)通过试算法求得最优水力参数zm,并由式(6)求得与其相对应的最优无量纲湿周Sm,再由式(10)求得与zm相对应的km值,具体计算成果见表1。

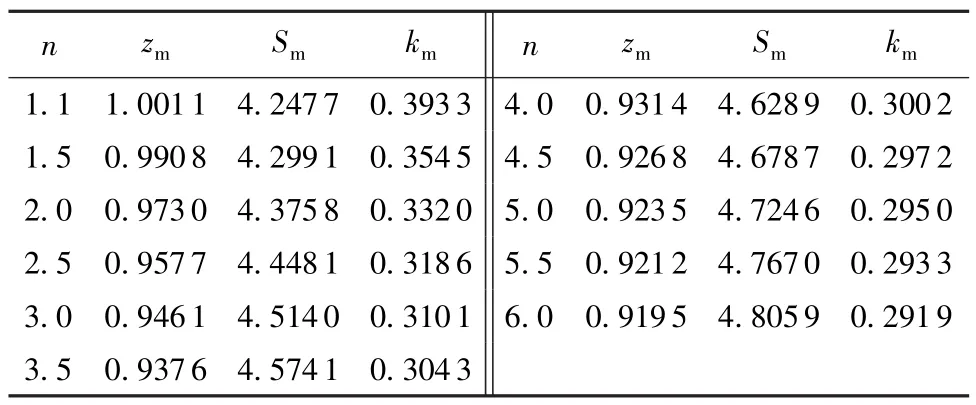
表1 与n值相对应的最优水力参数

由表1可见,当n为已知量时,相应的zm、Sm及km均可求得(当n值在表中两个给定值之间时,可采用内插法获得相应的zm、Sm及km),则由式(1) (8)(9)即可求得与最优水力参数相对应的断面设计特征值:

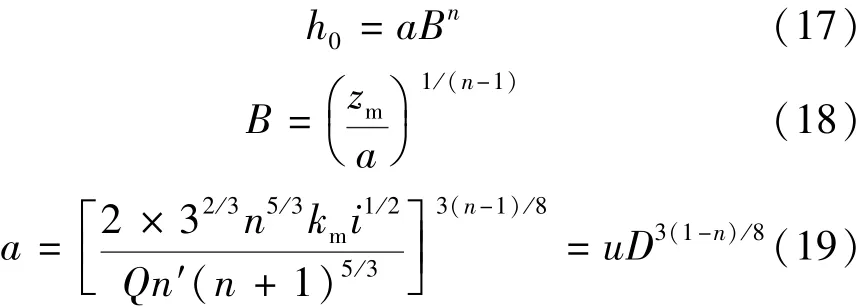
其中

式中:D为已知综合参数;u为抛物线形断面形状参数的系数。

3 最优抛物线方程指数

表1为在已知抛物线方程指数情况下的最优水力参数,在实际工程中,设计人员往往更关心当渠道的其他参数(流量、比降及糙率)一定情况下,如何选取抛物线方程指数才能获得最经济的设计断面,即最优抛物线方程指数。为此,本文利用上述研究成果开展进一步的分析。

将式(18)和式(19)分别代入式(3)及式(5)并整理可得

其中

式中f、p分别为抛物线形断面的断面系数及湿周系数。

利用式(24)和式(25)即可通过选取不同的n值,计算出与之相对应的f、p值。为便于实际工作,现将不同n值所对应的f、p的计算成果列于表2,并绘制f-n及p-n关系曲线,见图1。

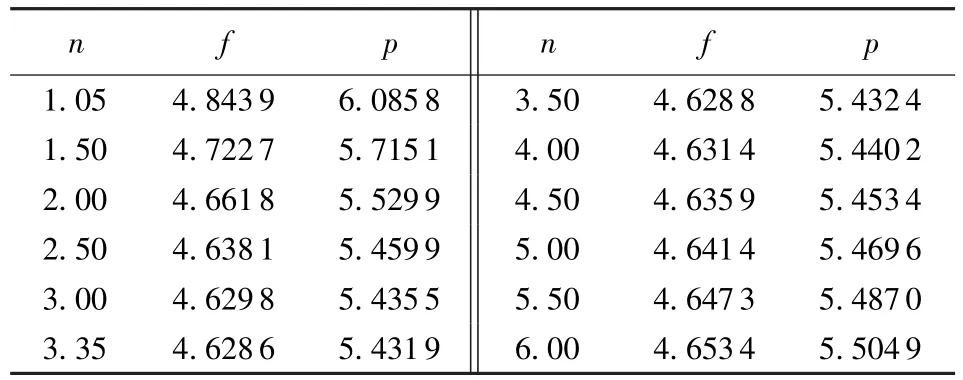
表2 与n值相对应的f、p值

图1 f-n、p-n关系曲线

由图1可见,当n=3.35时,f和p获得最小值,此时A及χ最小,因此n=3.35即为最优抛物线方程指数。

由表2可见,当渠道其他设计参数一定情况下, n=3.35断面的断面面积分别较n=1.5、2.0、5.0、6.0时的断面面积小2.03%、0.72%、0.28%及0.54%;护砌长度(即湿周)分别短5.21%、1.80%、0.69%及1.34%。因此,在实际工程中,采用最优抛物线形断面对有效减少工程量、降低工程造价具有重要意义。

4 算例

已知一灌溉用水渠道的设计过水流量Q= 50 m3/s,渠底的设计坡降为i=0.000 5,采用混凝土护砌,渠道糙率n′=0.014。选择最优抛物线形断面设计,并分别与n=1.5、2.0时的抛物线形断面及U形水力最优断面进行比较。

根据已知参数即可采用本文公式按以下方法完成求解计算:由表1及表2可得,当n=1.5时,zm=0.9908,f=4.7227,p=5.7151,由式(21)得u= 0.70183,由式(19)(22)(23)可分别求得a=0.480715, A=21.457m2,χ=12.182m,由式(17)(18)可分别求得h0=4.209 m,B=4.248 m。

采用同样方法也可分别求得当n=2.0、3.35情况下的断面水力参数,成果见表3。

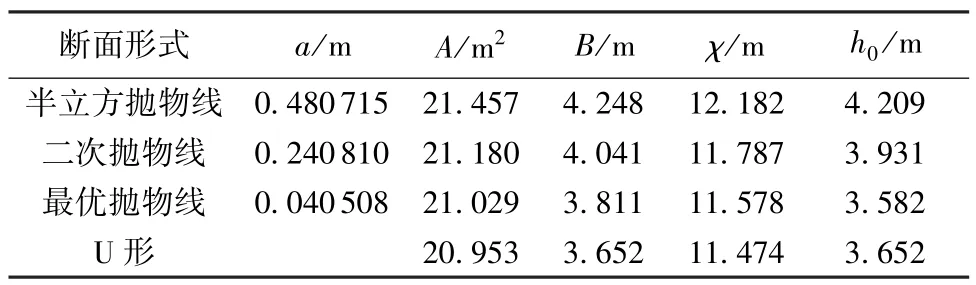
表3 抛物线形、U形水力最优断面计算成果

由表3可见,就渠道设计过水断面面积、湿周长度、水面宽度及正常水深而言,最优抛物线形断面与U形断面最接近,其断面面积及湿周仅较U形断面的断面面积及湿周大0.362%和0.906%;水面宽度较U形断面大4.35%,更有利于渠道边坡稳定及护砌施工;水深较U形断面小1.917%,更适合于中小型灌溉及排水渠道。而半立方抛物线及抛物线形断面的断面面积则较U形断面的断面面积分别大2.405%和1.083%;湿周分别大6.170%和2.728%;水面宽度分别大16.320%和10.652%;水深分别大15.252%和7.640%。综上可知,上述3种断面均不如最优抛物线形断面。

5 结语

本文通过对抛物形明渠过水断面均匀流方程的变形整理并采用近似积分的方法,得到了抛物线形明渠断面当抛物线方程指数n取大于1情况下任意数值时最优水力参数的简捷计算方法,使最优过水断面面积、湿周长度、水面宽度及正常水深的计算更加便捷实用;同时,本文在对抛物线形明渠过水断面最优水力参数进一步分析的基础上,提出了当渠道其他设计参数(流量、比降及糙率)一定情况下抛物线形断面的最优抛物线方程指数为n=3.35,并通过算例分析比较,较好地验证了其主要优点,可为该类工程或类似工程的优化设计提供参考和借鉴。

[1]魏文礼,杨国丽.立方抛物线形渠道水力最优断面的计算[J].武汉大学学报:工学版,2006,39(3):49-51. (WEI Wenli,YANG Guoli.Hydraulic calculation of optimal cross-section of cubic parabola channel[J]. Engineering Journal of Wuhan University,2006,39(3): 49-51.(in Chinese))

[2]张志昌,刘亚菲,刘松舰.抛物线形渠道水力最优断面的计算[J].西安理工大学学报,2002,18(3):235-237. (ZHANG Zhichang,LIU Yafei,LIU Songjian.Paralbolashaped channel hydraulic calcuayion of optimal crosssection[J].Xi’an University of Technology,2002,18(3): 235-237.(in Chinese))

[3]冷畅俭,王正中.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28(4):29-31. (LENGChangjian,WANGZhengzhong.Formulafor calculation contarcted water depth of cubic paraboa cross section[J].Journal of Yangtze River Scientific Research Institute,2011,28(4):29-31.(in Chinese))

[4]冷畅俭,王羿,王正中.抛物线形断面渠道共轭水深的直接计算公式[J].排灌工程机械学报,2013,31(2):132-136.(LENG Changjian,WANG Yi,WANG Zhengzhong. Explicit calculation equations for conjugate of channels in parabolic-shaped cross-section[J].Journal of Drainage and Irrigation Machinery Engineering,2013,31(2):132-136. (in Chinese))

[5]谢成玉,滕凯.三次抛物线形渠道断面收缩水深的简化计算公式[J].南水北调与水利科技,2012,10(1):136-138.(XIE Chengyu,TENG Kai.Simplified equation of contracted water depth in a channel having a cubical parzbola section[J].South-to-North Water Transfers and Water Science&Technology,2012,10(1):136-138.(in Chinese))

[6]赵延风,王正中,刘计良.抛物线类渠道断面收缩水深的计算通式[J].水力发电学报,2013,32(1):126-131. (ZHAO Yanfeng,WANG Zhengzhong,LIU Jiliang.Explicit epuation forcalculationofcontractedflowdepthsin channelsofparaboliccross-sections[J].Journalof Hydroelectric Engineering,2013,32(1):126-131.(in Chinese))

[7]滕凯.抛物线形断面渠道收缩水深简化计算通式[J].水利水电科技进展,2014,34(3):61-64.(TENG Kai. Simplified general formula for calcalation water depth in parabolic-shaped channel nieh contracted sectionc[J]. Advances in Science and Technology Water Resources, 2014,34(3):61-64.(in Chinese))

[8]张志昌.水力学[M].北京:中国水利水电出版社,2011.

[9]同济大学数学教研室.高等数学[M].上海:人民教育出版社,1978.

Calculation of open channel section optimum hydraulic parameters and parabolic index parabola//

ZHANG Liwei1, TENG Kai2
(1.River Management Office of Qiqihar City,Qiqihar 161006,China;2.Qiqihar Municipal Water Affairs Bureau,Qiqihar 161006,China)

A relatively systematic study on the optimum hydraulic parameter of parabolic transaction and the calculation of parabolic optimum index have been studied in this paper.Through sorting out the variants and calculating the approximate integration of the equation of uniform flow for such transaction,this essay presents the simplified formula for the optimum hydraulic parameter of the open-channel water-flowing transaction in case of a given parabolic equation index.By analyzing the simplified equation,we found a new optimum equation index of parabolic transaction to be 3.35 on the condition that other parameters of the open-channel such as water flow,gradient and roughness stay unchanged.Our finds also show that the presentation of the optimum hydraulic parameter serves as the basis for the further optimization design of parabolic transaction.Additionally,through the comparison of the optimum index of parabolic transaction and other hydraulic optimum transactions,the optimum index of parabolic transaction shows a higher economic indicator and therefore,it is worth extending the application.

parabola form channel;uniform flow in open channel;best hydraulic cross section;hydraulic parameter

TV131.4

:1006-7647(2014)05-0065-04

10.3880/j.issn.1006-7647.2014.05.013

201308-01 编辑:骆超)