Memetic 算法在水电站负荷优化分配中的应用

邓丽丽,杨 侃,周佳佳

(河海大学水文水资源学院,江苏南京 210098)

Memetic 算法在水电站负荷优化分配中的应用

邓丽丽,杨 侃,周佳佳

(河海大学水文水资源学院,江苏南京 210098)

针对求解水电站厂内经济运行中负荷优化分配问题时常出现的收敛性差、易早熟等问题,将基于全局搜索和局部启发式搜索相结合的Memetic算法应用于水电站厂内经济运行负荷优化分配模型,用有限制的初始种群生成法来克服水电站机组不稳定运行问题,采用育种算法作为局部搜索策略。三峡水电站厂内经济运行实例计算结果表明,有限制的初始种群生成法能够避开空蚀振动区的影响,保证机组的稳定安全运行;Memetic算法的全局搜索和局部启发式搜索策略能够扩大寻优范围,优化群体结构,提高算法的收敛能力。

水电站;负荷优化分配;厂内经济运行;Memetic算法;全局搜索;局部搜索

水电站厂内经济运行是在满足一系列约束条件的情况下,制定机组的启停次序,选择最优的工作机组台数和组合以及各运行机组间的负荷,以期获得电站运行的最大经济效益[1]。负荷优化分配是水电站厂内经济运行的关键子问题,该问题是指当给定了机组组合后,在满足各种约束条件的前提下,将系统负荷合理分配给各运行机组,使水电站机组的总耗水量最小[2]。最优的负荷分配可减小机组的运作损耗以提高机组运行的稳定性和安全性,减少发电耗水量以提高水资源的利用效率。因此,负荷优化分配不仅要考虑水电站发电机组最小、最大预想出力的限制条件,还不能忽略实际负荷分配中存在的机组空蚀振动区等严重影响水轮机稳定和安全运行的限制问题。负荷优化分配是一个复杂的多约束非线性优化问题,在以往的研究中,其主要的求解方法包括等微增率法[1]、动态规划法[3-4]、遗传算法[5-7]和微粒群算法[8]等。周冉等[3]在用动态规划法求解负荷最优分配方案的过程中,为了避开机组的空蚀振动区,对机组流量特性曲线出力落在空蚀振动区的部分进行惩罚处理;但当水电站机组数和解空间维数增多时,动态规划法会出现“维数灾”问题。张仁贡等[6]将遗传算法(genetic algorithm,GA)应用于水电站厂内经济运行,对机组的空蚀振动区在评价函数中用罚函数进行处理;但遗传算法不能有效地处理非线性约束,且当维数较高时,会影响算法的搜索效率,很容易使算法陷入局部最优,不便于水电站负荷分配问题的求解。李崇浩等[8]通过确定微粒群在多维空间中的最优位置来实现机组间的负荷优化分配,对飞入振动区的微粒进行惩罚来避开空蚀振动区,并引入遗传算法的交叉算子克服局部收敛问题;小范围的交叉虽可产生新个体,但具有局限性。

Memetic算法[9-10]是一种不同于遗传算法的全局优化算法,它不仅吸取了遗传算法全局搜索能力的优点,同时通过局部搜索策略来提高算法的局部搜索能力,为解决水电站厂内经济运行中的负荷优化分配问题提供了一种有效的方法。本文探讨一种以育种算法为局部搜索策略的Memetic算法在水电站负荷优化分配问题中的应用,并通过实例计算验证该算法求解水电站负荷优化分配问题的可行性和收敛性。

1 水电站厂内经济运行负荷优化分配模型

水电站厂内经济运行负荷优化分配的目的是当给定系统负荷和水电站水头时,使整个水电站耗流量最小。最佳的负荷分配需要使机组运行效率最高且保证机组稳定安全运行,故必须避开机组的空蚀振动区。水电站厂内经济运行负荷优化分配数学模型为

式中:Q为水电站运行机组的发电总耗水量;n为机组数;j为机组编号;cj为j号机组的开停机状态,取值0或1分别为机组关或开;Nj为j号机组的出力,即负荷;H为电站水头;qj(Nj,H)为j号机组在水头H、出力为Nj时的发电引用水量,通过由拟合得到的机组流量特性函数计算得到;P为系统对电厂的负荷要求;N1,maxj、N1,minj分别为水头H下j号机组预想出力的上、下限;N2,maxj、N2,minj分别为水头H下j号机组稳定运行区的上、下限;Zs为水库水位; Zs,min、Zs,max分别为水库允许的最低水位和最高水位;Qmin、Qmax分别为水库的最小和最大下泄流量;Zw为水库尾水位,根据下泄流量与尾水位的关系曲线线性插值得到。

上述模型中机组运行工况约束不仅考虑了机组预想出力的限制,还考虑了避开空蚀振动区的需要。机组运行区一般划分为空蚀振动区(包括禁止运行区和限制运行区两部分)和稳定运行区,划分需要依据机组机架振动、轴承摆度标准来确定。机组在禁止运行区运行时极易造成严重破坏;在限制运行区运行时存在一定程度的振动,长期运行可能会造成疲劳破坏;只有在稳定运行区中机组才能长期连续稳定安全运行。因此进行水电站厂内经济运行研究时,为了保证机组的稳定安全运行,必须避开机组的空蚀振动区,使机组一直运行在稳定运行区中。稳定运行区的上、下限是一个与水头H相关的区间,水头不同,机组对应的稳定运行区是不同的;而机组预想出力定义域也是一个与水头H相关的区间,故可通过求交集的方式将式(3)和式(4)转化为机组运行工况约束:

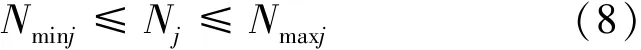
式中:Nmaxj、Nminj分别为水头H下j号机组的可行区域上、下限,可行区域是水头H下j号机组按照运行区划分避开了空蚀振动区的区域。

2 Memetic算法

Memetic算法是Moscato等在1992年提出的,该算法是一种基于人类文化遗传策略的群体智能优化算法,其局部搜索对象并不是种群空间内的普通个体,而是在各局部区域选出的优秀代表,但个体与个体之间的相互操作和遗传算法的遗传操作是相似的,因此,Memetic算法实质上是一种基于种群的全局搜索和基于个体的局部启发式搜索的结合体[9-10]。图1为Memetic算法的计算流程,Memetic算法采用的计算框架和操作流程与遗传算法相似,但它不局限于单纯的遗传算法,该算法在每次交叉和变异后均进行局部搜索,通过及早剔除不良个体,优化种群结构,加快了算法的收敛能力。

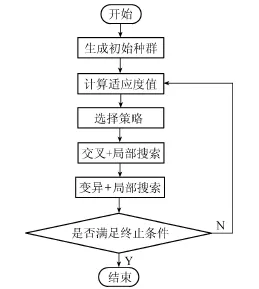
图1 Memetic算法的计算流程

2.1 初始种群的生成

Memetic算法中,初始种群的分布性质对算法的收敛性能有一定的影响。考虑到水电站水轮机运行区划分的特殊性,本文运用了一种有限制的初始种群生成法(以下简称有限制方法),在种群生成的过程中就将水轮机的出力直接限制在机组运行工况约束的最小、最大范围内,如某机组的运行工况约束出力范围为45～70 MW,那么其对应的出力取值范围为45～70 MW。因此,初始种群中的个体满足机组预想出力约束及避开空蚀振动区的要求。

机组出力编码和机组出力计算公式分别为

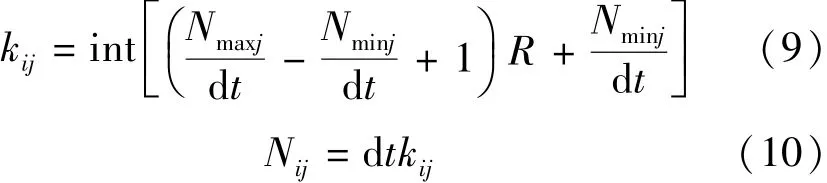
式中:kij为第i个个体j号机组出力编码;dt为控制精度即出力离散的步长;R为一个[0,1]的均匀随机数;int为取整函数;Nij为第i个个体j号机组出力编码对应的出力值。

2.2 适应度函数

水电站负荷优化分配模型中的约束条件主要包含负荷平衡约束(等式约束)和运行工况约束(不等式约束)两种。决策变量的运行工况约束即不等式约束采用有限制的方法处理。由于运行机组的总负荷不一定等于给定的负荷,因此负荷平衡约束包含在适应度函数中采用罚函数的方法来处理。适应度函数Fi表达式为

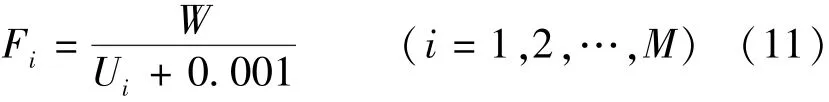
式中:W是一个较大的常数;M为种群的个体数;Ui为第i个母体所对应的式(1)和式(2)的增广目标函数值,见式(12)。

当运行机组的总负荷大于系统给定的负荷时,由于罚函数的作用,增广目标函数值Ui会增大;但当运行机组的总负荷小于系统给定的负荷时,由机组的流量特性曲线可知运行机组的总耗流量也会减小,这时适应度的大小难以判定,可能出现不满足约束条件的非可行个体适应度高的现象,无法保证种群的收敛。因此,在运行机组的总负荷小于系统负荷时,在增广目标函数中采用双重惩罚的方法以保证种群收敛:

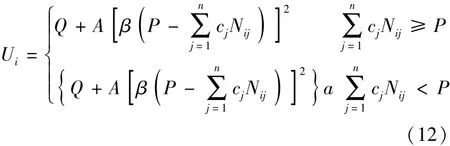
而对于约束条件中的水库下泄流量约束、水库下泄流量与尾水位关系约束及水库水位约束等其他约束条件在编程计算的过程中进行了验证,对不满足约束的个体进行适当的惩罚,让其在迭代过程中被淘汰。

2.3 选择策略

Memetic算法采用比例替换的选择策略:①根据个体适应度高低对种群中的个体进行排序;②选出种群中排名靠后的PsM(Ps为选择概率)个个体,再把排名靠前的PsM个个体复制一份;③用复制的排名靠前的PsM个个体替换排名靠后的PsM个个体。

比例替换的选择策略一定程度上使算法在进化初期保持种群的多样性且在进化的后期仍然具有对优良个体的选择能力,提高了算法的全局收敛性能。

2.4 交叉策略

在Memetic算法中,把经过选择后的M个个体随机地进行两两配对,配对的个体以交叉概率Pc按照算术交叉的方式进行交叉运算,从而得到新个体。交叉公式为

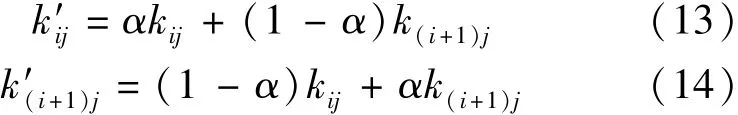
式中:kij、k(i+1)j分别为配对的两个个体j号基因的编码值;k′ij、k′(i+1)j分别为对应的交叉后得到的新个体j号基因的编码值;α为(0,1)上的随机数。

2.5 变异策略

Memetic算法采用非均匀的变异策略:对种群中的个体以变异概率Pm进行变异,在可以变异的个体染色体编码串中随机选取一个基因位,按下式对该基因位上的基因进行变异:

式中:kis、k′is为变异前后个体染色体编码串基因位上的编码值,s表示个体染色体编码串中基因位的位置;mis,max、mis,min分别为参数取值的上、下限; rand(2)指随机产生整数1或2;r为一个[0,1]的均匀随机数;t、g分别为当前进化代数和最大进化代数;B是一个系统参数,决定了随机扰动对进化代数g的依赖程度。

2.6 局部搜索策略

局部搜索是指采用一定的操作策略,对染色体某些基因位进行部分改变,以优化种群的分布结构,及早剔除不良个体。常用的局部搜索方法有爬山法、贪婪法、模拟退火法等,本文采用育种算法。该方法是一种局部搜索算法,其核心思想是模仿生物繁殖优良品种,通过选种→繁殖→再选种→再繁殖,不断选择品质优秀的种子,不断繁殖,直到种子对应的函数值达到全局最大[12-13]。

3 实例应用

三峡水利枢纽工程是一个具有防洪、发电、航运等多项综合效益的大型水利水电工程。三峡水电站装配单机容量为70万kW的混流式水轮发电机32台,其中左岸电站装配14台,右岸电站装配12台,地下电站装配6台,另电源电站装配单机容量为5万kW的电源发电机组2台,总装机容量2250万kW。本文仅对左岸和右岸的26台单机容量为70万kW的混流式水轮发电机组进行分析,从左岸到右岸,依次对其排序编号。

分别采用Memetic算法和遗传算法优化79 m水头下三峡水电站的负荷分配,考虑空载耗流量,并以出力5 000 kW作为控制精度。79 m水头下左岸VGS机组的稳定运行区为43万～69.5万kW,左岸ALSTOM机组为46.5万～68.5万kW,右岸东电机组为41.5万 ～66万kW,右岸ALSTOM机组为45万～70万kW,右岸哈电机组为41万～63.5万kW。由于模拟运算的随机性,对Memetic算法和遗传算法优化负荷分配的过程进行10次模拟,并取最好的一次作为最终优化结果。对于算法中的参数交叉概率Pc和变异概率Pm,为了不影响算法的收敛性能,均采用参数自适应的思想进行调整[14]。为了便于比较,两种算法中的选择概率Ps均为0.3,种群规模均为200。

3.1 育种规模分析

对于育种规模,以三峡水电站79 m水头下1720万kW负荷为例,用Memetic算法分别优化了相同计算工况下育种规模为种群规模10%～100%的情况。每种情况下搜索到的最小耗流量及搜索过程所需的时间随育种规模的变化见图2。由图2可知,育种规模越大,搜索到的解越好,而所需的计算时间也越长。考虑到算法实时性的要求,认为育种规模为种群规模的0.5时效果最好,因此,本文育种规模为100。

图2 最小耗流量随育种规模的变化曲线

3.2 终止迭代次数分析

同样以三峡水电站79 m水头下1720万kW负荷为例,用Memetic算法分别以迭代100次、200次、300次、400次、500次、600次、700次及800次作为终止条件进行模拟,每个终止迭代次数下模拟得到的最小耗流量随迭代次数的变化见图3。由图3可以看出,模拟得到的最小耗流量随终止迭代次数的增加而减小,并最终趋于稳定,以500次为界,小于500次时最小耗流量随迭代次数的变化较大,而大于500次时最小耗流量几乎没有改变。考虑到三峡水电站负荷优化分配的复杂程度,并结合计算机的性能和程序计算时间,本文选择500次作为终止迭代次数。

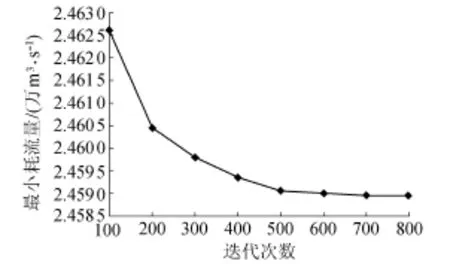
图3 最小耗流量随迭代次数的变化曲线

3.3 优化结果及分析

为了比较算法的收敛性能,采用两种算法在相同计算工况下优化了三峡水电站79 m水头下的不同负荷。表1为两种算法优化不同负荷的最小耗流量对比,最小耗流量为两种算法10次模拟最好的一次寻优结果。为了更直观地体现Memetic算法的搜索性能,选择两种算法10次模拟结果中最好的一次,对比了其搜索100次、200次、300次、400次及500次的最优适应度,结果见表2,并比较了其中两种负荷(1350万kW和1550万kW)的优化过程,如图4和图5所示,其他负荷的优化过程类似。

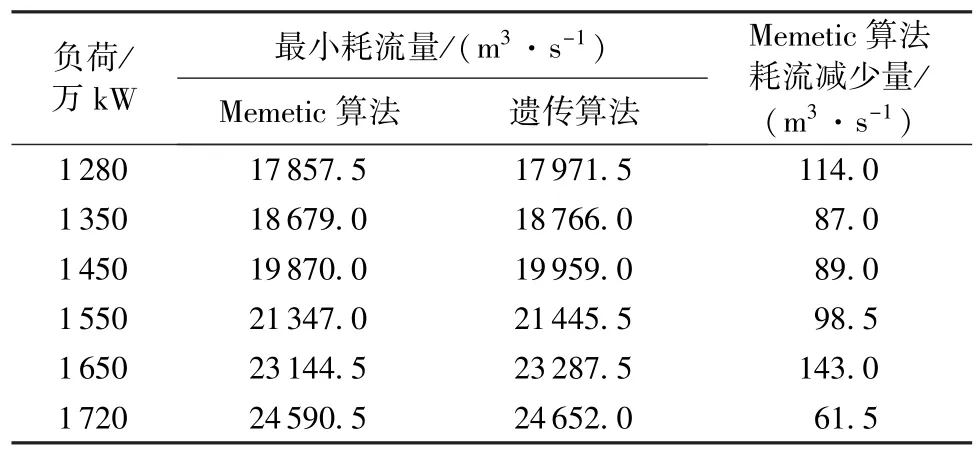
表1 79 m水头下两种算法优化不同负荷的最小耗流量对比

从表1可知,在相同的种群规模和迭代次数下,相比于遗传算法,Memetic算法在不同负荷下模拟的最小耗流量均有不同程度的减小;由表2可看出,随着迭代过程的推进,Memetic算法在不同负荷下模拟的最优适应度基本呈增加的趋势,而遗传算法的最优适应度大部分在进化到100代就不再增加了,在相同迭代次数下两种算法的最优适应度相差也越来越大;由图4、图5的关系曲线对比可以看出,遗传算法在优化负荷分配问题时,其目标函数值在进化到一定代数后就不再减小,相应的最优适应度也不再增加,而Memetic算法的目标函数值随迭代次数一直在减小,最优适应度也一直在增加,直到进化后期慢慢逼近最优解的过程中目标函数和最优适应度的变化幅度越来越小,最后不再变化。可见, Memetic算法模拟的结果明显优于遗传算法,说明Memetic算法能以较快速度收敛至全局最优,而遗传算法容易陷入局部最优。这是由于遗传算法在迭代过程中由于种群多样性下降,最优个体解比较早地出现收敛现象,易陷入局部最优,然而Memetic算法通过在最优个体附近进行局部搜索,总能找到更好的个体,跳出局部最优,其最优个体不易出现过早收敛现象,因此Memetic算法具有更强的收敛能力。

为了验证本文有限制方法能够保证所有运行机组的安全与稳定,相同计算工况下,用基于传统方法[6]考虑空蚀振动区的Memetic算法进行负荷优化分配,其中1350万kW和1550万kW两种负荷的最优分配方案见图6,负荷上、下限为机组运行工况约束的上、下限。其他负荷的最优分配方案基本一致。

从图6可看出,有限制方法得到的最优分配方案中所有机组均在稳定运行区中运行,而传统方法求得的最优分配方案中有少数机组运行在空蚀振动区,这说明有限制方法能够保证运行机组的稳定与安全。

表2 两种算法在不同迭代次数时的最优适应度

图4 目标函数值随迭代次数的变化曲线

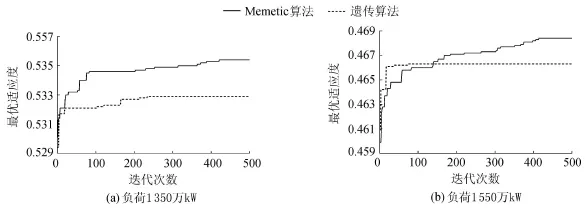
图5 最优适应度与迭代次数关系曲线

4 结 论

a.有限制方法能够保证所有运行机组运行在稳定运行区。

b.Memetic算法的交叉和变异策略继承了遗传算法的强全局搜索能力,能扩大寻优范围,提高算法的寻优质量。

c.Memetic算法的局部搜索策略可以优化种群分布,及早剔除不良个体,增强算法的局部寻优能力。

d.育种的局部搜索法依靠种子随机繁殖若干子代,且子代个体分散分布在可行空间的任意位置,能搜索到更好的解,使算法跳出局部最优,提高了算法的收敛性能。

[1]张勇传.水电站经济运行原理[M].北京:中国水利水电出版社,1998.

[2]何兰兰.水电站机组组合与负荷分配的短期经济调度[D].武汉:华中科技大学,2006.

[3]周冉,杨侃,郝永怀,等.考虑空蚀振动区的水电站厂内经济运行方法[J].中国农村水利水电,2011(6):153-155.(ZHOU Ran,YANG Kan,HAO Yonghuai,et al. Researchontheeconomicoperationmethodfor hydropower stations taking account of cavitation and vibration areas[J].China Rural Water and Hydropower, 2011(6):153-155.(in Chinese))

[4]薛鹏,曾季弟,林家洋,等.基于遗传算法和运行区划分的水电站厂内经济安全运行分析[J].水力发电学报, 2010,29(6):13-18.(XIE Peng,ZENG Jidi,LIN Jiayang,et al.Study of internal economic operation based on GA and operation region partition[J].Journal of Hydroelectric Engineering,2010,29(6):13-18.(in Chinese))

[5]王黎,马光文.基于遗传算法的水电站厂内经济运行新算法[J].中国电机工程学报,1998,18(1):64-66. (WANG Li,MA Guangwen.Genetic algorithm in hydro station economic dispatch[J].Proceeding of the CSEE, 1998,18(1):64-66.(in Chinese))

[6]张仁贡,韩桂芳,白家骢,等.遗传算法在水电站厂内经济运行中的应用[J].华北水利水电学院学报,2006,27 (1):61-64.(ZHANG Rengong,HAN Guifang,BAI Jiacong,et al.The application of genetic algorithm in inner-plant economical operation of hydropower station [J].JournalofNorthChinaInstituteofWater Conservancy and Hydroelectric Power,2006,27(1):61-64.(in Chinese))

图6 机组负荷最优分配方案

[7]刘国帅,杨侃,郝永怀,等.水库短期优化调度改进选择算子的遗传算法应用研究[J].中国农村水利水电, 2011(10):44-46.(LIU Guoshuai,YANG Kan,HAO Yonghuai,et al.Application of genetic algorithm based on advanced selection operator for short-term optimization operation of reservoir[J].China Rural Water and Hydropower,2011(10):44-46.(in Chinese))

[8]李崇浩,纪昌明,李文.微粒群算法在水电站厂内经济运行中的应用研究[J].水利水电技术,2006,37(1): 88-91.(LI Chonghao,JI Changming,LI Wen.Study on application of particle swarm optimization to in-plant economic operation of hydropower station[J].Water Resources and Hydropower Engineering,2006,37(1):88-91.(in Chinese))

[9]刘文君.Memetic算法研究与工程应用[D].武汉:华中科技大学,2007.

[10]李智欢.基于新型Memetic算法的电力系统无功优化研究[D].武汉:华中科技大学,2007.

[11]张慧.遗传算法在水电站群经济运行中的应用[D].南京:河海大学,2007.

[12]许必熙.育种算法简介[J].大众科技,2005(9):66-67.(XU Bixi.Breeding algorithms instruction[J]. Popular Science&Technology,2005(9):66-67.(in Chinese))

[13]田凯,许必熙.育种算法在组合优化计算中的应用[J].安徽农业科学,2012,40(20):10361-10362.(TIAN Kai,XU Bixi.Breeding algorithm and its application to combinatorial optimization calculation[J].Journal of Anhui Agricultural Sciences,2012,40(20):10361-10362.(in Chinese))

[14]SRINIVAS M,PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Transactions on Systems,Man and Cybernetics,1994,24 (4):656-667.

Application of Memetic algorithm to optimal load dispatch of hydropower station//

DENG Lili,YANG Kan,ZHOU Jiajia
(College of Hydrology and Water Resources,Hohai University,Nanjing 210098,China)

In this paper,we apply the Memetic algorithm,based on global search and local heuristic search,to the model of load distribution of hydropower station aiming to overcome problems such as the bad convergence and easy premature emerged frequently when dealing with optimal load dispatch of inner-plant economical operation of hydropower station.To do that,a method to overcome the problem of instable operation of hydropower station units is used to generate the initial population.Additionally,the local search strategy is based on breeding algorithm.Taking the inner-plant economical operation of Three Gorges Hydropower Station as a case study,the Memetic algorithm is compared with genetic algorithm. The results show that with the limited method to generate initial population,stable and safe operations of units are ensured by avoiding the influence of cavitation-vibration region.The global search and local search strategy are able to enlarge the searching range of the algorithm and optimize the population structure as well as improve the ability of convergence.

hydropower station;optimal load dispatch;inner-plant economical operation;Memetic algorithm;global search;local search

TV737;TV697.1

:A

:1006-7647(2014)05-0050-06

10.3880/j.issn.1006-7647.2014.05.010

2013-0722 编辑:熊水斌)

国家重点基础研究发展计划(973计划)(2012CB417006);“十一五”国家科技支撑计划(2009BAC56B03)

邓丽丽(1990—),女,江西宜春人,硕士研究生,主要从事水库(群)优化调度与经济运行研究。E-mail:denglili0312@126.com