乌牛新闸下游冲刷模型试验及经验公式适用性
2014-07-02田小平
田小平,王 斌,陈 剑
(1.温州市水利电力勘测设计院,浙江温州 325009;2.浙江省水利河口研究院,浙江杭州 310020)
乌牛新闸下游冲刷模型试验及经验公式适用性
田小平1,王 斌2,陈 剑1
(1.温州市水利电力勘测设计院,浙江温州 325009;2.浙江省水利河口研究院,浙江杭州 310020)
针对乌牛新闸闸下冲刷问题,建立水闸物理模型并观测闸下冲刷坑的形成及发展过程,研究冲刷坑位置及深度随时间的变化规律,并将试验成果与两种常用的冲刷公式计算结果进行对比分析,探索了冲刷公式在平原地区淤泥土质中的适用性。结果表明:当下游潮位较低时,过闸水流在防冲槽末端形成跌流,水流翻滚剧烈,对下游河道冲刷明显;随着汇合口河道地形的长期冲刷,汇合口附近的水跃逐渐消失;随着时间加长,冲刷坑位置整体有所下移,冲刷深度从快速增大逐渐趋于稳定;在平原地区淤泥土质中,毛昶熙公式计算的闸下最大冲刷深度与试验成果较为一致,具有较好的适用性。
乌牛新闸;闸下潮位;冲刷坑;最大冲刷深度;典型潮位过程;动床试验;经验公式
平原地区河道断面往往宽而浅,水闸建成后常常存在单宽流量大、闸下局部流速大、水流流态复杂、水流对河床的冲刷力大等问题,因此水闸下游冲刷一直是水闸工程的重点和难点。
研究水闸下游冲刷的方法主要有现场观测、模型试验、理论分析和数值模拟。史斌等[1]通过曹娥江枢纽闸下冲刷模型试验,提出了采用台级法模拟非恒定过程,探讨了洪峰流量和冲刷历时对冲刷坑深度的影响,并得出了较为合理的冲刷坑深度。王斌等[2]采用三维数值模拟软件Flow-3D对乌牛新闸的水动力和闸下冲刷情况进行了模拟,结果表明该软件对低水头闸下三维水流数值模拟和冲刷研究具有较好的适用性。
本文建立水闸物理模型,观测乌牛新闸下冲刷坑的形成及发展过程,研究冲刷坑的位置及深度随时间的变化规律,并将模型试验成果与两种常用的冲刷公式计算结果进行对比分析,探索冲刷公式在平原地区淤泥土质的适用性,进而为水闸工程建设提供科学依据。
1 工程布置
乌牛新闸位于浙江省温州市乌牛溪流域下游与瓯江汇合处,为中型排水及挡潮闸,承担着乌牛溪流域的防洪挡潮和排涝任务,设计排水标准为20年一遇,挡潮标准为50年一遇[3]。乌牛溪流域集水面积86.0 km2,上、中游为山区和丘陵,下游为平原和低丘区。水闸上游河道宽 70.0 m,下游引河长约110.0 m。闸址处为深厚软土地基,河床表层以下依次为淤泥及淤泥质黏土,其中淤泥层厚度18~24m,淤泥质黏土层厚度8~11 m。淤泥层泥沙中值粒径d50在0.0019~0.0034mm之间,平均值为0.0023 mm; d60在0.0028~0.0060mm之间,平均值为0.0038mm。
乌牛新闸闸室为5孔,每孔净宽8.0 m,中间的隔离墩将闸室划分为左侧3孔(1~3号孔)和右侧2孔(4、5号孔),闸槛高程为-1.0 m,设计流量776.0 m3/s。从上游至下游,水闸工程主要包括上游护底段、闸室段、下游消能防冲段、下游两侧接线堤等几部分,水闸纵剖面如图1所示。
乌牛新闸的设计特征水位和潮位是:①闸上正常蓄水位2.70m,闸上设计洪水位4.26m,闸上设计低水位-1.00 m;②闸下设计高潮位5.35 m,设计低潮位-2.87 m。
乌牛新闸控制运行工况的技术条件是:①当闸上水位高于闸下潮位且超过正常蓄水位时,开启水闸进行排水;当闸上水位低于闸下潮位或降低至正常蓄水位时,关闭水闸。②尽量在闸上水位超过正常蓄水位且比闸下潮位高0.2~0.3 m时开闸排水,避免在闸下无水时开闸。
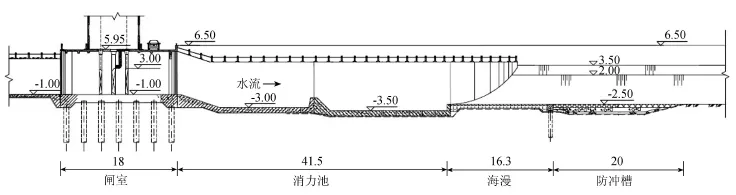
图1 水闸纵剖面图(单位:m)
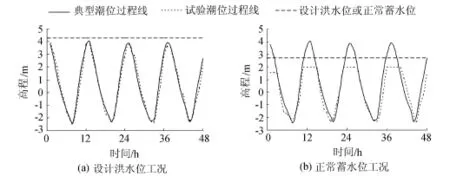
图2 动床试验的典型潮位过程线
2 模型试验
2.1 试验设计
模型试验按照重力相似准则设计[4],为正态模型,几何比尺为1∶40,模型范围上游取至闸上260m,下游取至闸下400 m,闸下河道与瓯江汇合口横向宽度约280 m。选取模型沙首要考虑泥沙的起动相似准则,其次考虑水下休止角的相似准则。根据乌牛新闸闸下河道及瓯江汇合口附近的地质资料,河床表层以下依次为淤泥及淤泥质黏土。采用沙玉清[5]和张瑞瑾等[6]泥沙起动流速公式计算,按比尺换算后,所需模型沙的中值粒径约为0.44 mm,因此模型沙可采用天然沙,且该材质能直观地反映闸下泥沙的水下休止角,可以较好地模拟冲刷坑形态,满足乌牛新闸闸下局部冲刷试验的要求。
动床试验主要模拟闸下最大冲刷深度及冲刷坑形态,闸上水位为固定值,闸下潮位考虑瓯江典型潮位过程和固定潮位两种控制方式,瓯江典型潮位过程中的最高潮位4.04 m,最低潮位-2.37 m,为2年一遇设计潮型;多年平均潮位0.47m,多年平均低潮位-1.64 m。上、下游水位、潮位采用自动水位和流量尾门控制系统实时调控,通过电脑及机械控制达到水位、潮位变化的目的。试验共有6组方案,试验方案详见表1。
动床试验的典型潮位过程线如图2所示,当闸上水位为正常蓄水位、闸下潮位接近2.00 m时,模型沙基本没有起动,因此没有模拟闸下潮位高于2.00 m的情况。
2.2 试验结果与分析
表2为瓯江典型潮位过程中两种工况在不同冲刷时间的最大冲刷深度。从表2可以看出,正常蓄水位工况的冲刷形态与设计洪水位工况较接近,仅量值较小,随着时间的增长,冲刷坑位置整体有所下移,冲刷深度从快速增大逐渐趋于稳定。
闸下冲刷后的地形等高线如图3所示,闸下右岸堤脚在不同位置的冲刷深度如图4所示。
从表2和图3、图4可以看出:①当下游潮位较高时,闸下流态整体较为平顺,泥沙起动较少;当下游潮位较低时,过闸水流在防冲槽末端形成跌流,水流翻滚剧烈,对下游河道造成明显冲刷,大量泥沙被带入下游河道,随着汇合口河道地形冲刷变深,汇合口附近水跃逐渐消失。②受模型沙沉降速度不相似影响,闸下局部起动的泥沙迅速在下游河道落淤,因此闸下游130 m以外河道的冲刷深度相对偏小,通过经验公式计算平均冲深约4.8 m。
另外,通过试验还观测了瓯江潮位为多年平均潮位0.47m以及多年平均低潮位-1.64m这两组特征潮位工况的冲刷坑形态,其与瓯江典型潮位过程的冲刷结果基本接近。当下游潮位为多年平均潮位0.47 m时,闸下流态整体较为平顺,冲坑相对较浅,最大冲刷深度约为5.1 m;当下游潮位为多年平均低潮位-1.64 m时,水流在防冲槽末端形成跌流,流态与典型潮位过程的低潮位时刻相似,最大冲深为10.6 m,冲刷坑位置较典型潮位过程更靠近防冲槽末端。
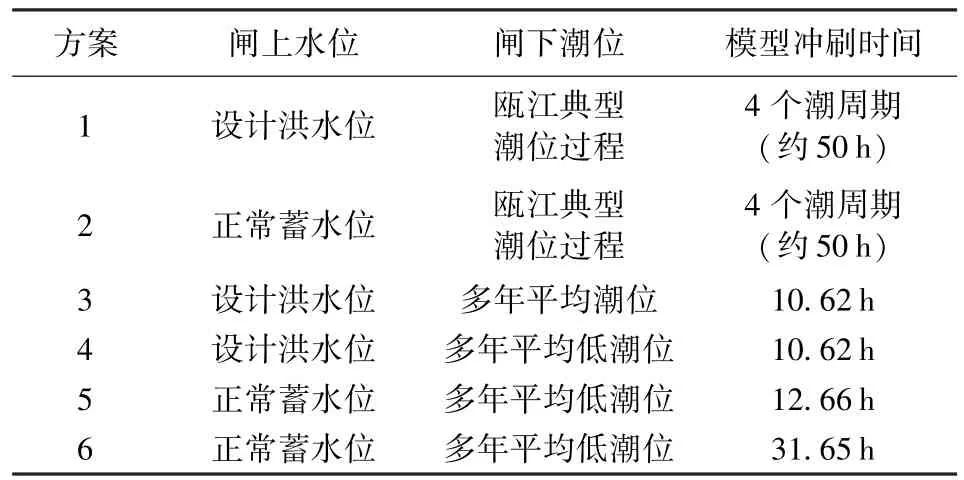
表1 动床试验方案
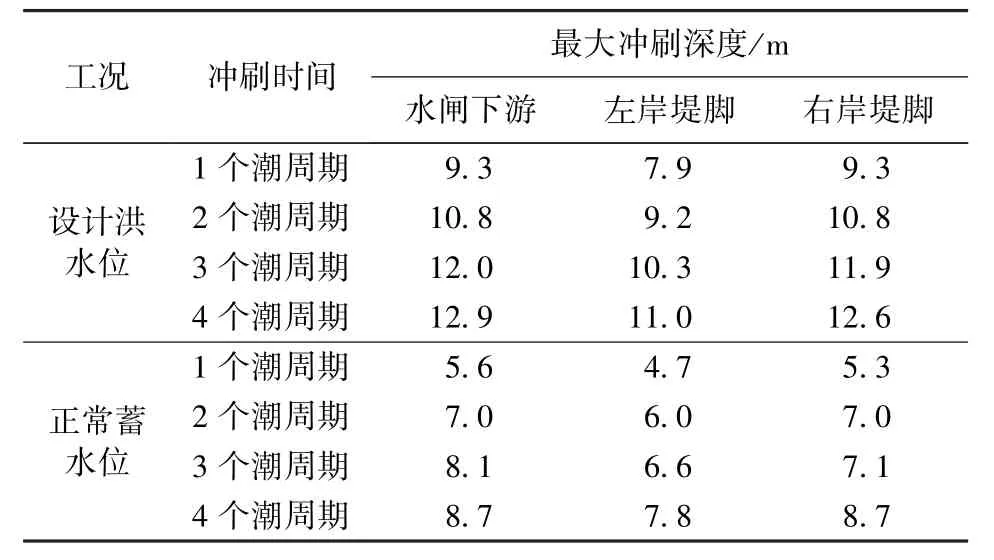
表2 典型潮位过程的最大冲刷深度
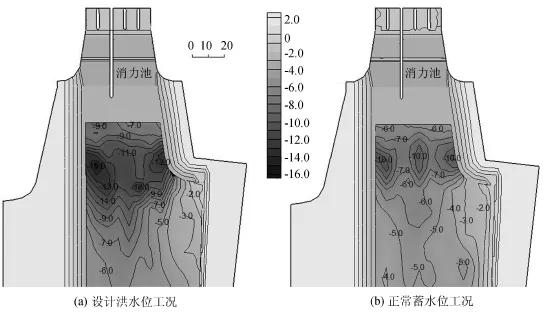
图3 闸下冲刷后的地形等高线(单位:m)
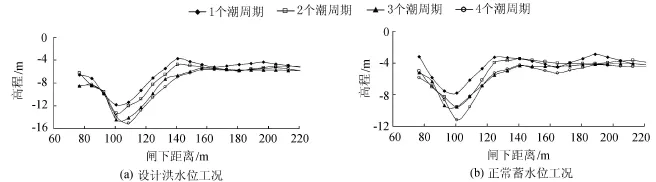
图4 闸下右岸堤脚在不同位置的冲刷深度
3 冲刷公式及计算结果
3.1 冲刷公式
目前,计算最大冲刷深度的公式较多,常用的是SL265—2001《水闸设计规范》[7]中推荐的公式和南京水利科学研究院毛昶熙[8]公式,其中 SL 265—2001《水闸设计规范》推荐的公式为

式中:dm为海漫末端河床冲刷深度,m;qm为海漫末端单宽流量,m3/(s·m);v0为河床土质允许不冲流速,m/s;hm为海漫末端河床水深,m。毛昶熙公式为
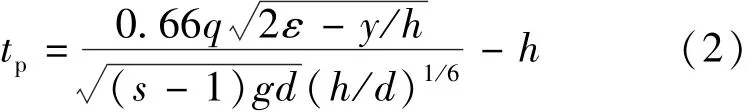
式中:tp为河床冲刷深度,m;q为河床单宽流量, m3/(s·m);ε为流速分布不均匀性的动量修正系数,取1.1;d为河床土粒直径,取0.0038 mm;s为土粒质量与水质量的比值,取2.65;g为重力加速度, m/s2;h为水深,m;y为最大流速的位置高度,m。
对比式(1)和式(2)可以看出,前者形式较为简单,考虑的因素较少,而后者考虑了河床土质、水流扩散和水深等因素,形式较复杂。
3.2 冲刷计算
利用式(1)和式(2)计算乌牛新闸最大冲刷深度,计算结果见表3。

表3 最大冲刷深度计算结果
由表3可知,正常蓄水位工况时,式(1)计算结果较式(2)小3.3 m,两者的比值为56.0%;设计洪水位工况时,式(1)计算结果较式(2)小5.5 m,两者的比值约为 57.4%。总之,式(1)计算结果比式(2)偏小。
将计算结果和试验结果进行比较发现,在正常蓄水位工况和设计洪水位工况下,式(2)计算的冲刷深度分别为7.5 m和12.9 m,试验得到的冲刷深度分别为8.7 m和12.9 m,两者的结果比较接近,由此说明在平原地区淤泥土质条件下,采用毛昶熙公式计算水闸冲刷深度是合适的,而SL265—2001《水闸设计规范》推荐的公式计算结果偏差较大。
4 结 论
a.在正常蓄水位和设计洪水位工况下,当下游潮位较高时,水闸下游流态整体较为平顺,泥沙起动较少;当下游潮位较高时,过闸水流在防冲槽末端形成跌流,水流翻滚剧烈,对下游河道造成明显冲刷,冲刷坑位置靠近防冲槽末端,最大冲刷深度分别为8.7 m、12.9 m;随着时间增长,冲刷坑位置整体有所下移,冲刷深度从快速增大逐渐趋于稳定;水闸下游局部起动的泥沙迅速在下游130 m以外河道落淤,冲刷深度也相对偏小。
b.在正常蓄水位和设计洪水位工况下,毛昶熙公式的计算结果与试验结果较为一致,说明在平原地区淤泥土质条件下,采用毛昶熙公式计算水闸冲刷深度是合适的,而SL265—2001《水闸设计规范》推荐公式计算结果偏差较大。
[1]史斌,包中进,陆芳春.曹娥江枢纽闸下冲刷试验研究[J].浙江水利科技,2004(6):32-34.(SHI Bin,BAO Zhongjin,LU fangchun.Experimental research on scour of Cao'e Sluice[J].Zhejiang Hydrotechnics,2004(6):32-34.(in Chinese))
[2]王斌,王月华,包中进.浙江乌牛新闸闸下三维水流冲刷数值模拟研究[J].人民长江,2013,44(13):55-57. (WANG Bin,WANG Yuehua,BAO Zhongjin.Numerical simulation research on downstream three-dimensional flow and scouring of new Wuniu Sluice in Zhejiang Province [J].Yangtze River,2013,44(13):55-57.(in Chinese))
[3]田小平.温州市乌牛新闸工程初步设计[R].温州:温州市水利电力勘测设计院,2010.
[4]王斌.永嘉县乌牛新闸水工模型试验研究报告[R].杭州:浙江省水利河口研究院,2010.
[5]沙玉清.泥沙运动学引论[M].北京:中国工业出版社, 1965.
[6]张瑞瑾,谢鉴衡,陈文彪.河流动力学[M].北京:中国工业出版社,1961.
[7]SL265—2001 水闸设计规范[S].
[8]毛昶熙.水工建筑物下游局部冲刷综合研究[M].北京:水利电力出版社,1959.
Model experiment and adaptability of empirical formula research on downstream flow and scouring of new Wuniu sluice//
TIAN Xiaoping1,WANG Bin2,CHEN Jian1
(1.Wenzhou Institute of Hydraulic Design,Wenzhou 325009,China;2. Zhejiang Institute of Hydraulics and Estuary,Hangzhou 310020,China)
Elaborate on the downstream scouring problem,a physical model is established to observe the formation and development process of the scouring pit.Furthermore,the scouring pit location and depth variation with time is studied. Additionally,the results of physical model experiment and the empirical formula are compared and analyzed to explore the adaptability of the empirical formula in the plains of silt soil.The main conclusion of this work is that during low tide of the downstream,the lockage water forms drop flow in the scour stone cages causing significant erosion on the downstream.With the long-term erosion at the confluence of river terrain,the hydraulic jump near the confluence disappears gradually in the fixed bed physical model.With longer time,the scouring pit location shifts downward and the scouring pit depth increases from fast to a stable state.Moreover,in the plains of silt soil,the maximum scouring pit depth calculated from the Mao Chang-xu empirical formula of Nanjing Hydraulic Research Institute(NHRI)is consistent with the results of the physical model experiment,which means that the formula can be applied in practice.
new Wuniu sluice;downstream tide level;scouring pit;maximum scouring pit depth;typical tidal process; movable-bed experiment;empirical formula
TV653
:A
:1006-7647(2014)04-0075-04
10.3880/j.issn.1006-7647.2014.04.016
2013-0929 编辑:周红梅)
田小平(1974—),男,重庆开县人,高级工程师,主要从事水利工程规划设计工作。E-mail:370643181@qq.com
