径流贝叶斯概率预报在水库发电优化调度中的应用

韩义超,徐 炜,张 弛,彭 勇,王本德

(1.辽宁省水利水电勘测设计研究院,辽宁沈阳 110006; 2.重庆交通大学河海学院,重庆 400074;3.大连理工大学建设工程学部,辽宁大连 116024)

径流贝叶斯概率预报在水库发电优化调度中的应用

韩义超1,徐 炜2,3,张 弛3,彭 勇3,王本德3

(1.辽宁省水利水电勘测设计研究院,辽宁沈阳 110006; 2.重庆交通大学河海学院,重庆 400074;3.大连理工大学建设工程学部,辽宁大连 116024)

为了充分考虑降雨、径流预报的不确定性和降低水库发电调度模型的复杂性,采用贝叶斯概率水文预报系统(BFS)耦合降雨预报的不确定性和径流预报模型本身的不确定性来定量描述径流预报的不确定性,发布径流确定性预报、概率预报和概率预报期望值;结合随机动态规划(SDP)模型和贝叶斯随机动态规划(BSDP)模型来制定发电调度图;以浑江桓仁水库流域为背景,采用美国国家天气局的全球预报系统(GFS)发布的10 d降雨预报信息作为预报模型输入,模拟桓仁水库的发电调度过程。模拟结果表明基于径流贝叶斯概率预报的水库发电调度能有效提高水库的发电效益和保证率。

水力发电;数值降雨预报;径流概率预报;贝叶斯理论;随机动态规划;桓仁水库

近年来,随着科学技术的不断发展,数值气象预报的精度不断提高,预见期也不断延长,其中美国的全球预报系统(global forecasting system,GFS)和中国气象局的T213系统均能够提供相对可信的中期环流形势以及10～15 d的降雨预报信息。将数值降雨预报信息应用于水库发电优化调度中,有利于提高水库径流预报的预见期和精度,从而有利于水库发电调度决策。在降雨和径流预报信息的实际使用中,合理处理预报信息的不确定性是关键。

在水库实时发电调度中,预报的径流过程属于不确定性信息,局限了动态规划等确定性算法的应用,而随机动态规划(stochastic dynamic programming, SDP)模型能够在算法中耦合径流预报信息的不确定性,与水库多阶段决策的特点具有较高的契合性。经典SDP模型将预报径流信息视为准确的或假定误差不变的,调度中直接用于决策[1-3]。径流预报的不确定性主要受降雨预报精度的影响,且随着预见期的延长,降雨预报和径流预报的不确定性也逐渐增加,即试图精确地描述径流非常困难[4-5],因此Karamouz等[6-8]在水库运行中运用贝叶斯理论来灵活处理入流的概率信息,并在随后的研究中建立了贝叶斯随机动态规划(bayesian stochastic dynamic programming,BSDP)模型。通过对BSDP模型的改进,使其在电力系统需求分析、季节性入流不确定性对发电调度的影响评价等方面得到了应用[9-15]。然而BSDP模型的入流概率信息只是对径流预报不确定性的某一或某几方面进行量化分析,没有充分考虑降雨预报的不确定性和径流预报模型本身的不确定性。当模型在融合多元信息描述径流预报信息的不确定性时,调度模型的复杂性和“维数灾”问题随信息量的增加而加剧。

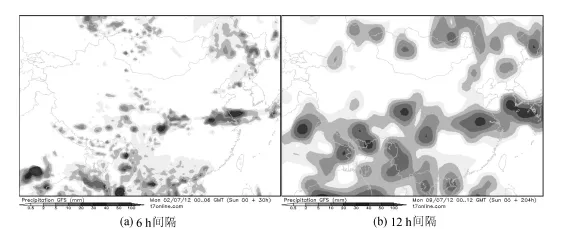
图1 GFS发布的降雨预报分布

鉴于目前在水库发电调度中耦合降雨和径流预报信息所存在的问题,本文参考 Krzysztofowicz等[16-20]提出的贝叶斯概率水文预报系统(bayesian forecasting system,BFS),将数值降雨预报不确定性与水文预报不确定性分别量化;然后通过全概率公式将二者耦合起来,得到水文预报不确定性的解析解,同时得到径流概率预报值、概率预报期望值和确定性径流预报值;最后,基于SDP模型和BSDP模型的发电优化调度图,依据径流预报信息分别模拟桓仁水库的发电调度决策,并对模拟发电调度的效益和稳定性进行比较与分析。

1 概率预报及优化调度模型的建立

1.1 GFS降雨预报系统

GFS降雨预报系统由美国国家环境预报中心研制,是全球应用最广泛的数值预报业务系统之一。该数值天气预报系统按格林威治时间在每日的0、6、12和18时向公众发布未来1～15 d各地区降雨情况,如图1所示。该降雨预报系统分为两个部分:一部分为精度较高的未来1～8 d降雨预报系统,以6 h为间隔发布数值预报,如图1(a)所示;另一部分为精度较低的未来9～15 d降雨预报系统,以12 h为间隔发布数值预报,如图1(b)所示。

1.2 径流预报模型

本文采用多元线性回归模型和新安江模型分别建立流域非汛期和汛期的旬径流预报模型[13-14]。多元线性回归模型以上旬降雨和径流信息和本旬降雨信息作为影响因子,建立非汛期旬径流预报模型[21-22];汛期建立以日降雨量作为输入的新安江模型,模拟汛期未来旬的径流过程,通过累加得到旬径流量[23]。采用1968—2000年的实测降雨和径流资料对模型参数进行率定,将此阶段作为模型参数率定期;模型参数验证阶段采用2001—2010年实测降雨资料模拟径流,并与实测径流对比检验模型预报能力。模型参数率定期、验证期和预报期精度的详细内容可参见文献[13]。

1.3 贝叶斯概率水文预报系统BFS

流域径流预报不确定性可分为降雨预报不确定性和水文预报不确定性[19-20]。通过统计分析实测降雨量与GFS预报降雨量获得降雨的不确定性。水文预报不确定性包括径流本身的不确定性以及径流预报模型结构和参数带来的不确定性,可通过实测降雨量模拟径流并与实测径流的对比来进行定量分析。BFS采用全概率公式耦合水文预报不确定性与降雨预报不确定性,并提供了研究概率水文预报的框架,如图2所示。水文模型的预报径流所属区间为Ht,实测径流所属区间为Qt(在优化模型计算时,采用所属区间的中值作为区间代表值进行计算)。

1.3.1 水文预报不确定性分析

图2 旬径流概率预报模型结构

1.3.2 降雨预报不确定性分析

统计GFS发布的未来10 d降雨量和实测降雨量,并分别表示为w和r。将降雨量进行等级划分,各等级表示为Ry(y为等级数);可得到当预报降雨量w为 Ry时,实际降雨量 r的概率分布函数为f(Ry);根据f(Ry)可得到不同概率条件{Ph:h=1,2,…,z}所对应的一组实测降雨量序列{rp1,rp2…,rpz}。根据GFS发布的10d预报降雨量获得预报降雨量条件下,不同概率对应的实测降雨量序列;然后通过所建立的径流预报模型模拟计算获得对应的径流量序列可通过上述关系计算出当预报径流发生在Ht区间的概率:

1.3.3 不确定性综合

当t-1时段实测径流量在Qt-1区间时,GFS预报降雨发生等级为Ry,采用全概率公式,t时段实测径流将发生在区间Qt的概率为

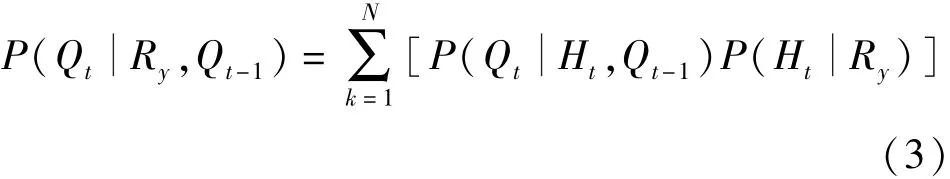
式中:k为t时段预报径流发生区间;N为t时段预报径流划分区间数。

1.4 水电站调度优化模型

1.4.1 优化调度模型目标函数

优化调度模型以调度期1～T时段内总发电量期望值最大为目标函数:

式中:Kt为t时段初的库水位;Lt为t时段决策末水位;E[B(Kt,Qt,Lt)]为t时段期望发电效益函数; B(Kt,Qt,Lt)为t时段惩罚后的发电量效益函数; b(Kt,Qt,Lt)为t时段水电站实际发电效益函数,由耗水率、总泄流量计算获得;α和β为惩罚系数;e为保证出力;Δt为计算时段长度。

1.4.2 优化调度模型递归函数

建立经典SDP模型和BSDP模型,它们的径流描述过程分别如图3(a)(b)所示。

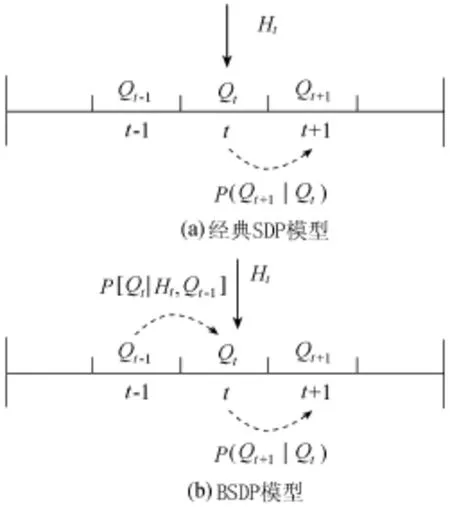
图3 优化调度模型径流描述过程

a.SDP模型递推方程。SDP模型的径流描述过程如图3(a)所示,将预报径流Ht视为较准确的情况下水库发电调度优化模型递推方程为

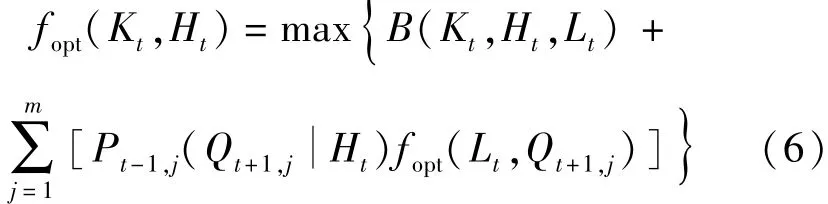
式中:fopt(Kt,Ht)为t时段初水位Kt和预报径流区间Ht条件下,优化模型递推方程效益函数;j为t+1时段实测径流发生区间;m为t+1时段实测径流划分区间数。

b.BSDP模型递推方程。BSDP模型采用贝叶斯理论描述径流状态转移过程及径流的不确定性,模型径流描述过程如图3(b)所示,模型递推方程为

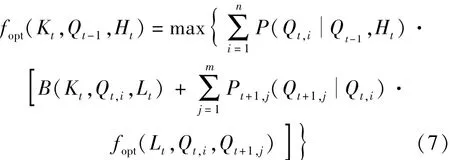
式中:fopt(Kt,Qt-1,Ht)为t时段初水位Kt、预报径流区间Ht和t-1时段实测径流区间Qt-1条件下,优化模型递推方程效益函数;i为t时段实测径流发生区间;n为t时段实测径流划分区间数。

1.5 径流预报信息与发电调度的耦合

将BFS系统制定的确定性径流预报(确定性预报)、径流区间等级概率预报(概率预报)和径流概率预报期望值(概率预报期望值)分别作为SDP和BSDP模型径流预报信息输入指导水库发电调度决策。由于BFS以径流区间形式发布概率预报信息,因此当采用概率预报信息作为径流输入信息时,以发生概率最大的径流区间等级和当前控制水位查调度图得到决策出力。当采用确定性预报和概率预报期望值作为径流输入信息时,通过预报径流结果和当前水库控制水位查调度图得到决策出力。

2 工程实例

2.1 流域概况

桓仁水库位于东经124°43′～126°50′、北纬40° 40′～42°15′,地处浑江中游我国东北暴雨中心北部边缘,流域面积10400km2,流域植被良好,多年平均年雨量为860 mm,70%的雨量集中在6—9月,大洪水发生在7月下旬至8月中旬。

桓仁水库径流过程可分封冻期、融雪期与丰水期3个阶段。①封冻期从11月至次年3月,期间径流量小且相对稳定,主要由地下径流补充,封冻期采用多元线性回归模型进行径流预测。②融雪期从3月末至4月末(即春汛),径流受封冻期流域降雪量、温度等因素影响,往往致使该阶段径流深大于降雨量。在此期间,采用多元线性回归模型和新安江模型进行径流预报,处于由多元线性回归模型向新安江模型过渡的阶段。此阶段新安江模型对流域下垫面初值不断校正,因此径流预报以多元线性回归模型为主。③丰水期从5月至10月,径流量主要由降雨产生,该阶段采用新安江模型进行径流预报。

2.2 径流概率预报

2.2.1 GFS降雨预报不确定性分析

根据资料收集情况,利用2001—2010年5—10月GFS每日8:00发布的未来10 d降雨预报,并与实际降雨量进行统计分析。根据桓仁水库流域水文特点将GFS降雨预报信息分成3个阶段进行分析,即汛前期5—6月;主汛期7—8月;汛后期9—10月。将各阶段GFS预报降雨量分为4级,等级划分标准如表1所示。

对预见期内各预报等级的实际发生降雨量进行统计,由于各阶段第4级的样本较少,因此将3个阶段的第4级进行合并。通过Kolmogorov检验法以给定显著性水平α=0.05时对各阶段各预报等级条件下实际降雨量的分布进行非参数假设检验,得出5—6月、7—8月的第3级与合并后的第4级均满足0≤x的正态分布;其余等级均满足P-Ⅲ型分布,各等级实际降雨概率分布类型及参数见表2。

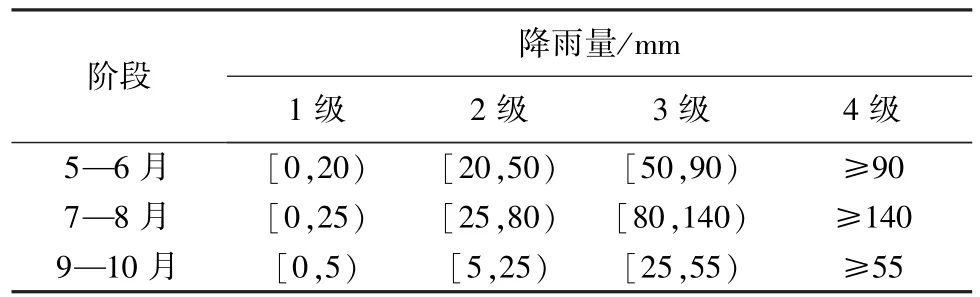
表1 GFS降雨预报等级划分标准

表2 各等级实际降雨概率分布类型及参数

2.2.2 水文模型不确定性分析

采用马尔柯夫链过程来描述t-1时段径流量与t时段径流量的关系,采用径流先验概率Pt,ij来描述径流的不确定性,表示t-1时段实测径流量Qt-1在区间i,t时段实测径流量Qt发生在区间j的概率。由于只有1968—2000年历史实测径流资料,计算得到的径流状态转移概率偶然性较大,因此,基于1968—2000年历史实测径流的统计规律,采用季节性自回归模型得到1 000年模拟径流过程,并将各旬径流划分为4个等级,计算径流状态转移概率矩阵,图4为7月下旬各实测径流等级条件下,8月上旬实测径流发生在各等级的转移概率矩阵。

图4 7月下旬至8月上旬实测径流状态转移概率矩阵

利用实测降雨资料模拟径流与实测径流的差异反映了水文模型结构、参数和流域下垫面情况估计等因素的不确定性,其概率矩阵即为似然概率矩阵,表示t时段径流预报Ht在区间k时,实测径流Qt发生在区间j的概率。采用1968—2000年实测降雨模拟径流与实测径流建立似然概率矩阵,图5为8月上旬各径流预报等级条件下,实测径流发生的似然概率矩阵。

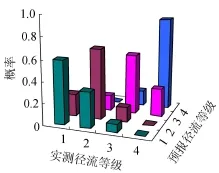
图5 8月上旬预报径流区间的似然概率矩阵

在径流预报的不同时期,根据t-1时段实测径流等级和t时段预报径流等级,使用公式(1)可更新该时段后验概率,图6为8月上旬的后验概率矩阵。

2.2.3 旬径流概率预报

利用BFS综合考虑GFS降雨预报和径流预报模型的不确定性,发布旬确定性径流预报和考虑不确定性的概率预报和径流期望值,表3为2010年发布的丰水期各旬概率预报的解析解。

根据SL250—2000《水文情报预报规范》规定径流中长期预报误差以多年变幅的20%作为评定标准。2001—2010年丰水期5—10月旬径流预报期望值与确定性预报的合格率统计结果见表4。

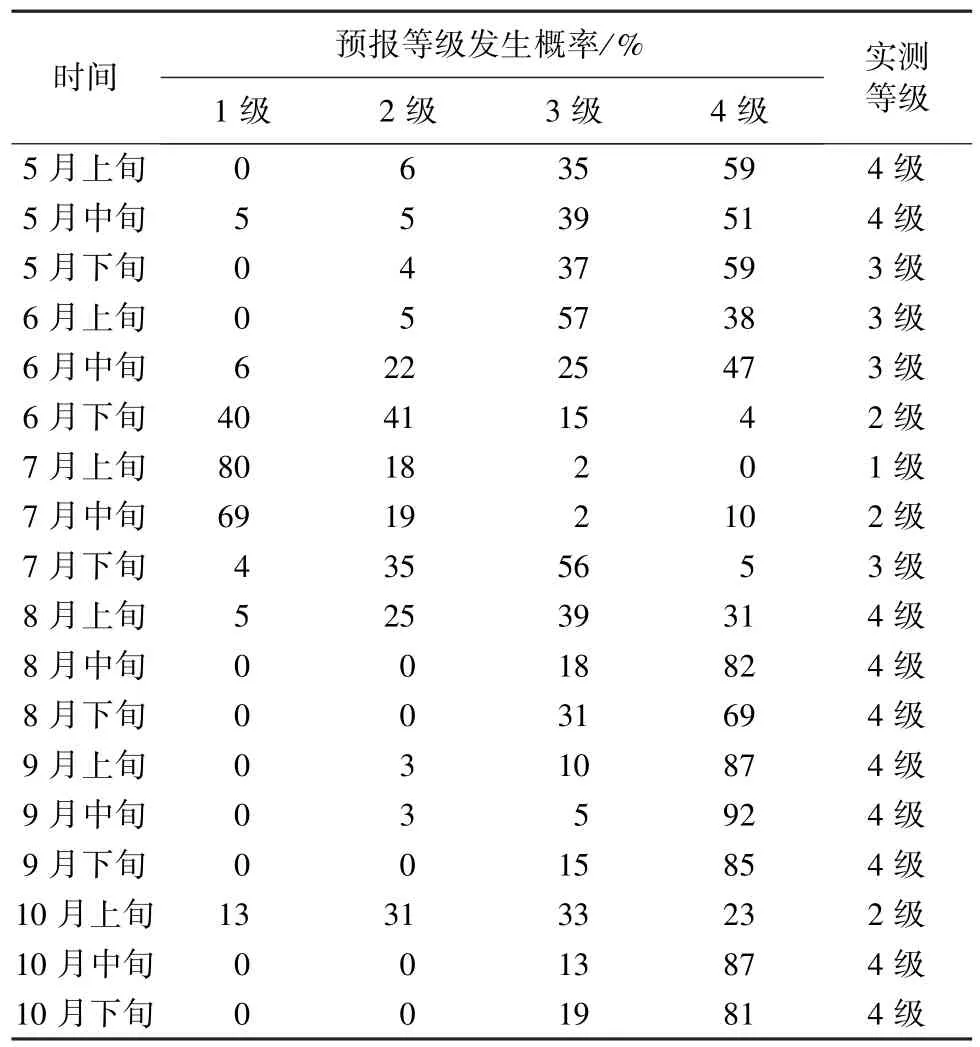
表3 2010年丰水期径流预报等级发生概率分布

表4 径流概率预报期望值和确定性预报合格率

图6 8月上旬的后验概率矩阵

2.3 水电站发电调度模拟

2.3.1 优化调度决策图

分别采用SDP和BSDP模型制定水库发电调度图。图7为8月上旬基于SDP模型优化制定的桓仁水库发电优化出力图,其中a表示8月上旬预报径流量等级。图8为8月上旬基于BSDP模型优化制定的发电优化出力图,其中b表示7月下旬实测径流量发生等级。根据上旬实测径流量等级、本旬预报径流量等级和当前水库控制水位查图8可获得水库8月上旬决策出力。

图7 基于SDP模型的8月上旬桓仁水库发电优化出力

2.3.2 水电站发电调度模拟

以确定性动态规划(dynamic programming,DP)模型推求的2001—2010年发电调度过程作为理想决策过程,以SDP和BSDP模型制定的发电优化调度图为基础,采用BFS发布的确定性预报、概率预报和概率预报期望值作为径流信息输入,模拟决策水库2001—2010年发电调度过程。采用年平均发电量、纳什系数以及决策出力满足系统出力的可能性作为评价指标[24-25],纳什系数用于评价各方案模拟的决策过程与理想决策的贴近程度,各方案模拟调度评价指标统计结果见表5。

图8 基于BSDP模型的8月上旬桓仁水库发电优化出力

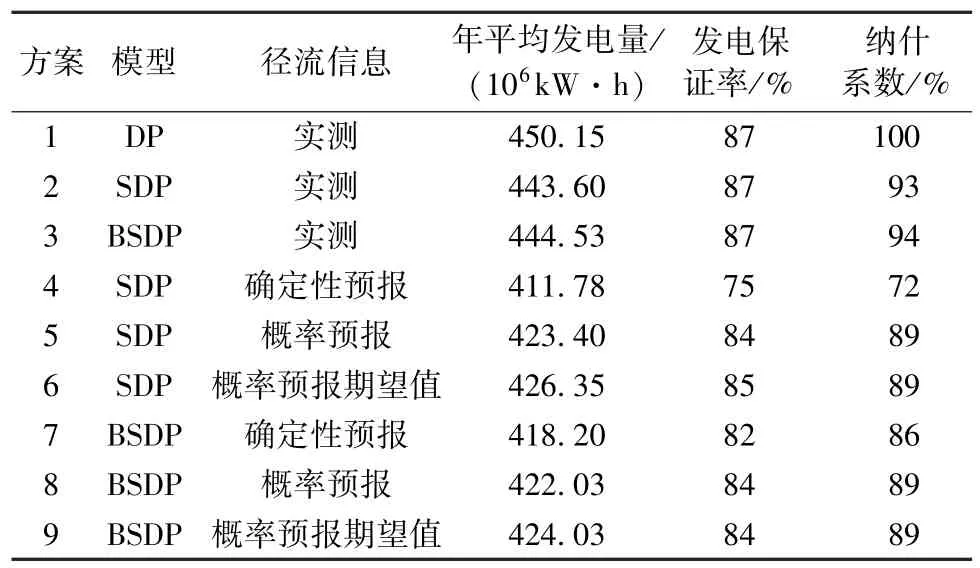
表5 不同模型方案发电调度模拟计算结果

方案2、3的发电量都低于方案1,结果是合理的,这是因为方案2、3只利用了下一个时段的实测径流信息,而方案1利用了当前时段以后所有的实测径流信息。比较方案4和7可知,在确定性预报信息条件下,BSDP模型优于SDP模型,这是由于SDP模型只采用马尔科夫链描述径流状态转移,而BSDP模型采用贝叶斯理论同时描述了径流状态转移和径流预报不确定性,因此在决策中直接使用确定性预报信息时,BSDP模型比SDP模型具有更强的抗不确定性。

比较方案5、6、8、9可知,SDP模型和BSDP模型中利用概率预报信息(概率预报值或概率预报期望值)来决策发电调度,模拟调度评价指标接近,这是由于这4个方案都充分考虑了径流的不确定信息,也说明将径流不确定性描述与优化调度模型相分离是可行的。

3 结 语

本文采用BFS分别与SDP模型和BSDP模型相耦合的方法来提高水库的发电效益。由于BFS考虑了降雨信息、模型及径流本身的不确定性,其预报结果与确定性预报径流相比有校正效果,所以在概率预报信息条件下SDP模型和BSDP模型效率相近,说明所建模型和耦合方法是可行的,且此时SDP模型比BSDP模型计算量更少,更简洁易懂,独立的SDP模型和BFS系统具有更强的模块化。

[1]DUTTA B,Houck M H.A stochastic optimization model for real-time operation ofreservoirs using uncertain forecasts[J].Water Resource Research 1984,20(8): 1039-1046.

[2]DUTTA B,BURGES S J.Short-term,single,multiple purpose reservoir operation:importance of loss function and forecast errors[J].Water Resource Research,1984, 20(9):1167-1176.

[3]STEDINGER J R,SULE B F,LOUCKS D P.Stochastic dynamicprogramming modelsforreservoiroperation optimization[J].Water Resources Research,1984,20 (11):1499-1505.

[4]ROULIN E,VANNITSEM S.Skillofmedium-range hydrological ensemble predictions[J].Journal of Hydrometeorology,2005,6(5):729-744.

[5]MASCARO G,VIVONI E,DEIDDA R.Implications of ensemble quantitative precipitation forecasterrorson distributed streamflow forecasting[J].Journal of Hydrometeorology,2010,11(1):69-86.

[6]KARAMOUZ M.Forecast uncertainty in reservoir operation[C]//Proceedings of the 15th Annual Water Resources Conference,Critical Water Issues and Computer Applications.New York:ASCE,1988.

[7]KARAMOUZ M.Bayesian decision theory and fuzzy sets theory in systems operation[C]//Proceedings of the 17th AnnualWaterResourcesConference,Optimizingthe Resources for Water Management.New York:ASCE, 1990.

[8]KARAMOUZ M,VASILIADIS H V.Bayesian stochastic optimization of reservoir operation using uncertain forecasts[J].Water Resource Research,1992,28(5): 1221-1232.

[9]KIM Y O,PALMER R N.Value of seasonal flow forecasts in bayesian stochastic programming[J].Water Resources Planning and Management,1997,123(6):327-335.

[10]MUJUMDAR P P,NIRMALA B.A bayesian stochastic optimization model for a multi-reservoir hydropower system [J]Water Resour Manage,2007,21:1465-1485.

[11]周惠成,王峰,唐国磊,等.二滩水电站水库径流描述与优化调度模型研究[J].水力发电学报,2009,28(1): 18-23.(ZHOU Huicheng,WANG Feng,TANG Guolei,et al.Study on the runoff description and optimal operation models for Ertan hydropower station[J].Journal of Hydroelectric Engineering,2009,28(1):18-23.(in Chinese))

[12]唐国磊,周惠成,李宁宁,等.一种考虑径流预报及其不确定性的水库优化调度模型[J].水利学报,2011,42 (6):641-647.(TANG Guolei,ZHOU Huicheng,LI N,et al.Optimaloperation modelforhydropowerstation considering the inflow forecast and uncertainty[J].Journal of Hydraulic Engineering,2011,42(6):641-647.(in Chinese))

[13]徐炜,张弛,彭勇,等.基于降雨预报信息的梯级水电站不确定优化调度研究I:聚合分解降维[J].水利学报, 2013,44(8):42-51.(XU Wei,ZHANG Chi,PENG Yong,et al.Stochastic optimization operation for cascade hydropower reservoirs by using precipitation forecasts I. Using aggregation-decomposition methodology to reduce high computationalcosts[J].JournalofHydraulic Engineering,2013,44(8):42-51.(in Chinese))

[14]徐炜,彭勇,张弛,等.基于降雨预报信息的梯级水电站不确定优化调度研究 Ⅱ:耦合短、中期预报信息[J].水利学报,2013,44(10):1189-1196.(XU Wei,PENG Yong,ZHANG Chi,et al.Stochastic optimization operation for cascade hydropower reservoirs by using precipitation forecasts ii-coupling short and medium-term information [J].Journal of Hydraulic Engineering,2013,44(8):42-51.(in Chinese))

[15]TANG G L,ZHOU H C,LI N,et al.Value of mediumrange precipitation forecasts in inflow prediction and hydropower optimization[J].Water Resour Manage,2010, 24:2721-2742.

[16]KRZYSZTOFOWICZ R.Bayesian model of forecasted time series[J].Water Resource Research,1985,21(5):805-814.

[17]KRZYSZTOFOWICZ R,KELLY K S.Hydrologic uncertainty processor for probabilistic river stage forecasting[J].Water Resource Research,2000,36(11): 3265-3277.

[18]KRZYSZTOFOWICZ R,HERR H D.Hydrologic uncertainty for probabilistic river stage forecasting: precipitation-dependent model[J].Journal of Hydrology, 2001,249(1/2/3/4):46-68.

[19]KRZYSZTOFOWICZ R,MARANZANO C J.Hydrologic uncertainty processor for probabilistic stage transition forecasting[J].Journal of Hydrology,2004,293(1/2/3/ 4),:57-73.

[20]KRZYSZTOFOWICZ R,MARANZANO C J.Bayesian system for probabilistic stage transition forecasting[J]. Journal of Hydrology,2004,299(1/2):15-44.

[21]梁国华,王国利,王本德,等.大伙房跨流域引水工程预报调度方式研究[J].水力发电学报,2009,28(3):32-36.(LIANG Guohua,WANG Guoli,WANG Bende,et al. Study on forecast based operation mode for Dahuofang inter-basin water transfer project[J].Journal of Hydroelectric Engineering,2009,28(3):32-36.(in Chinese))

[22]梁国华,习树峰,王本德,等.基于BP神经网络的旬降雨径流相关预报模型[J].水力发电,2009,35(8):10-12.(LIANG Guohua,XI Shufeng,WANG Bende,et al. Ten-day correlation forecast model of rainfall and runoff based on BP neural network[J].Water Power,2009.35 (8):10-12.(in Chinese))

[23]詹道江,叶守泽.工程水文学[M].北京:中国水利水电出版社,2000.

[24]HASHIMOTO T,STEDINGER J R,LOUCKS D P. Reliability,resiliency and vulnerability criteria for water resources system performance evaluation[J].Water Resource Research,1982,18(1):14-20.

[25]SURESH K R.Modeling for irrigation reservoir operation [D].Bangalore,India:Indian Institute of Science,2002.

Building optimization model for reservoir hydropower generation using Bayesian forecasting system and stochastic dynamic programming//

HAN Yichao1,XU Wei2,3,ZHANG Chi3,PENG Yong3,WANG Bende3
(1.Liaoning Hydro& Power Design Institute,Shenyang 110006,China;2.College of River and Ocean Engineering,Chongqing Jiaotong University,Chongqing 400074,China;3.Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian 116024,China)

In this paper,the Bayesian Forecasting System(BFS)is presented to address the uncertainties of inflow forecast and precipitation forecast as well as to reduce the complexity of the reservoir hydropower generation model.The BFS,based on Bayesian decision theory and total probability formula,is applied to quantitatively depict the uncertainties of inflow forecast by analyzing the uncertainties of hydrological model,inflow and precipitation forecast.Furthermore,the BFS is also used to develop a deterministic inflow forecast(DIF),the probabilistic quantitative inflow forecast(PQIF)and expectations forecast.Besides that,Stochastic Dynamic Programming(SDP) and Bayesian Stochastic Dynamic Programming(BSDP)are combined to formulate the hydroelectric operating policies.Finally,by using information of the 10 days lead time precipitation forecast of Global Forecast System(GFS)and taking Huanren Reservoir as a study case, the simulation of hydropower generation operating for this reservoir is provided.The simulation results show that the power generation dispatching based on the combination of BFS with SDP model can effectively improve the power generation efficiency and stability of the reservoir.

hydropower generation;precipitation forecast of GFS;probabilistic quantitative inflow forecast;Bayesian theory;stochastic dynamic programming;Huanren Reservoir

TV697.1+1;TV214

:A

:1006-7647(2014)04-0039-07

10.3880/j.issn.1006-7647.2014.04.009

2013-1231 编辑:周红梅)

水利部公益性行业专项(201001024);国家自然科学基金(51109025);教育部博士点基金(20100041120004)

韩义超(1967—),男,辽宁盖县人,教授级高级工程师,主要从事水利水电勘测设计工作。E-mail:hanyichao@163.com

徐炜(1985—),男,重庆人,讲师,博士,主要从事水库水电站发电优化调度研究。E-mail:xuwei19850711@163.com