桩周土开挖条件下桩基础屈曲稳定性分析
2014-07-02贾强李际平张全立张鑫
贾强,李际平,张全立,张鑫
(1.山东建筑大学土木工程学院,山东济南250013;2.山东省建筑结构鉴定加固与改造重点实验室,山东济南250013;3.鲁商置业股份有限公司,山东济南250014)
桩周土开挖条件下桩基础屈曲稳定性分析
贾强1,2,李际平1,2,张全立3,张鑫1,2
(1.山东建筑大学土木工程学院,山东济南250013;2.山东省建筑结构鉴定加固与改造重点实验室,山东济南250013;3.鲁商置业股份有限公司,山东济南250014)
利用桩基础支撑既有建筑,下方开挖土方施工地下室是一种既有建筑地下增层的有效方法。随着桩周土的开挖,桩基础的稳定性会降低。文章利用ANSYS程序建立桩的二维有限元模型,桩周土用弹簧单元模拟,其线刚度用m法取值,通过特征值分析和非线性加载可分别获得桩基承载力的上限、桩基承载力的极限荷载和失稳时的变形曲线。结果表明:桩顶为自由端的桩基础,随着桩周土开挖深度的增加,其稳定性系数明显降低;相同开挖条件下,桩周土的m值和桩基截面边长越小,其桩基的稳定性系数越小;桩顶或桩身设置水平约束构件后,有效减小了计算长度,其稳定性系数比桩顶为自由端的桩基础提高了1.2~2.9倍,且开挖深度越深、桩周土m值越小,其效果提高的越明显。
桩周土开挖;屈曲稳定性;数值分析
0 引言
对于埋置在土体中的桩基础,计算桩身轴心抗压强度时,一般不考虑压曲的影响,即取稳定系数φ=1.0。但对于桩上部没有土体约束的高承台桩,应对桩的压曲稳定性进行验算[1]。按照JGJ 94—2008《建筑桩基技术规范》第5.5.3条的规定,可根据桩顶约束情况、桩身露出地面的自由长度、桩的入土深度、桩侧和桩底土质条件确定计算长度[2]。研究桩基础屈曲稳定的难点在于桩周土体的约束作用不易确定,Forsesn曾提出了拼柱式高桥墩桩的稳定性问题[3]。胡人礼基于m法提出了一组桩身计算长度lc的经验计算公式,现仍被有关规范采用[4]。有学者采用引入变分法、最小势能原理、伽辽金法能量法等对桩的屈曲稳定性进行理论研究[5]。另有部分学者采用钢管桩、铜桩、钢轨桩、木桩以及铝桩进行桩的屈曲稳定性试验研究,取得了大量的研究成果[6-10]。但这些研究成果多是基于势能驻值原理的特征值方法,所获得的临界荷载值是实际失稳临界荷载值的上限,在实际工程中偏于不安全。邹新军基于第二类稳定问题,采用无单元伽辽金法对高承台桩的稳定性进行了分析,考虑了长细比、埋置率等影响因素对稳定性的影响,提出了桩身屈曲临界荷载的计算方法[5]。
既有建筑物地下空间开发的核心技术是桩基础托换和土方开挖。在既有建筑物下方兴建地下室时,需要运用原桩基础或增设新的桩基础支撑上部建筑物,才可开挖建筑物下方的土方[11]。土方开挖过程中,随着桩周土减少,桩基础暴露,桩的屈曲稳定性会明显降低。利用基础托换技术对既有建筑物地下增层的北京市音乐堂改建工程,为了防止桩基失稳,选用了8 m深的人工挖孔端承桩的方案,桩径达到1 m[12]。贾强针对地下增层中钢管托换桩的受压稳定性进行了试验研究,提出了底端固定、顶端铰接的钢管桩计算长度系数[13-14]。然而,既有建筑地下增层过程中桩基础稳定的相关研究较少,限制了地下增层技术的应用和推广。文章利用数值分析的方法,研究了桩周土开挖过程中,桩基础的稳定性变化规律,为既有建筑地下增层提供了技术支持。
1 数值分析
1.1 数值分析算例
桩基础为下方嵌岩的混凝土方桩,混凝土材料弹性模量为E=2.5×1010Pa,泊松比v=0.17,选用非线性本构关系,其应力—应变关系曲线如图1所示。桩的截面边长选取0.4 m和0.8 m,桩的长度取20 m。桩的约束状态除了桩底嵌岩对自由度全约束之外,桩顶分为自由端和有水平支撑构件(梁、板或承台)约束,桩身分为桩周土未开挖、桩周土部分开挖和桩周土部分开挖后设置新的水平构件等三种约束状态。
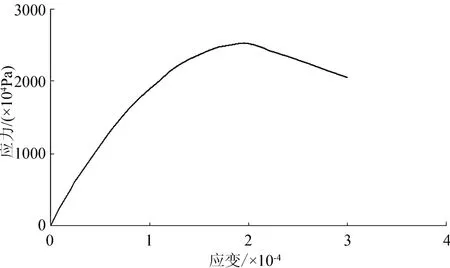
图1 混凝土本构关系曲线图
假定桩周土为均匀土质,为体现桩周土体对桩的水平约束作用,将土体水平作用假定为“土弹簧”,其水平反力系数采用“m”法取值[15],根据JGJ 94—2008《建筑桩基技术规范》5.7.5条的规定,对于水平反力系数较低的淤泥、饱和湿陷黄土,“m”取值范围为2~4.5 MN/m4;而水平反力系数较大的密实砾砂、碎石土,“m”取值范围为100~300 MN/m4[2]。本算例中,为了减少桩身单元的数量,桩的划分单元的网格尺寸为1m。因此,“土弹簧”的竖向间距取为1 m,与精密划分(0.2 m)的算例相比有4%的误差,但工程中尚能接受。“土弹簧”的水平刚度取值见表1,水平支撑构件水平刚度取为2×1010N/m。

表1 “土弹簧”的水平刚度
1.2 数值分析建模
采用ANSYS有限元程序二维建模。桩身采用PLANE42实体单元,土体弹簧和梁、板等水平构件用COMBIN14单元模拟。考虑平面外失稳因素的影响,将桩垂直方向的截面尺寸通过设置实体参数的方式进行定义。桩身单元采用映射划分,网格竖向间距为1 m,生成的节点能与土体弹簧的竖向位置相对应。土体弹簧外侧节点和桩身底部节点的自由度全部定义为0。有限元模型如图2所示。

图2 数值分析模型图
1.3 数值分析的策略
首先在桩顶施加单位荷载(1 N),利用ANSYS线性特征值屈曲分析可以了解屈曲形状,同时预测出屈曲载荷的上限,为非线性屈曲分析提供加载值的参考。其次,将屈曲载荷的上限值作为集中荷载施加在桩顶节点上,同时打开大变形、应力刚化、弧长法求解等设置进行非线性分析。计算达到设定的子步数(本计算设定了1000步)后会自动停止。
在后处理的时间历程分析模块中,得到桩顶节点水平位移随时间步的变化曲线。例如,m值取2.5 MN/m4、桩边长0.4 m、桩周土开挖15 m时,桩顶施加的集中荷载(屈曲分析特征值)为4.312× 105N,计算得到桩顶的水平位移随时间步的变化曲线如图3所示。
在非线性分析中,桩顶荷载是分了多个子步逐步施加在桩顶上,荷载的子步数和时间步成倒数关系。如图3所示,桩顶水平位移随时间步的增大而增加,到达0.6636后开始变小。说明荷载增加到该时间步时桩基础已达到极限荷载,相应的极限荷载值应是桩顶施加的集中荷载值乘以该时间步,即

得到该时间步(桩基失稳时)桩基础水平方向的位移等值线,同时估算出桩的嵌固深度和计算长度等。
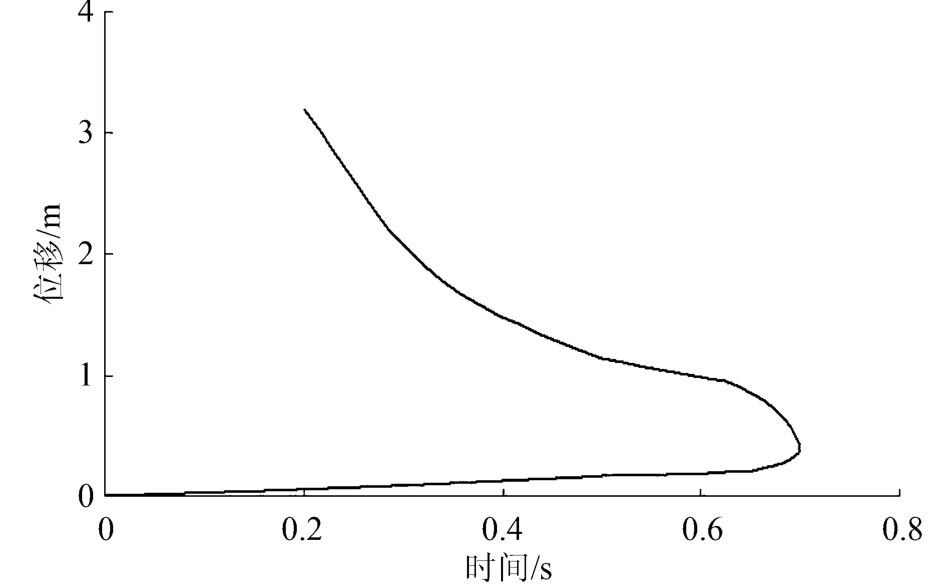
图3 桩顶水平位移随时间步变化曲线图
2 结果与分析
2.1 桩顶为自由端桩基屈曲极限荷载和稳定性系数
(1)初始化全局参数,具体包括信号的采样频率,符号率,载波频率,载波的幅度,设置4种不同FSK信号的频率,信噪比的最小值、最大值和增益值。
通过数值分析,可以得到桩周土为淤泥、饱和湿陷黄土(m=2.5 MN/m4)和密实砾砂、碎石土(m=250 MN/m4),边长为0.4和0.8 m的混凝土方桩,在桩周土未开挖或开挖深度分别为1、2、3、4、5、10和15 m等情况下桩的屈曲极限荷载。
通常轴心受压构件的稳定性按式(1)计算为

式中:N为轴心压力,N;A为截面面积,m2;f为材料强度,Pa;φ为稳定性系数。
因此,当通过数值分析得到桩的受压极限荷载,并且混凝土的极限抗压强度和截面面积已知的情况下,可反算出桩的稳定性系数。
稳定性系数和开挖深度的关系曲线如图4所示。
桩周土m=2.5 MN/m4,桩的边长为0.4 m,不同开挖深度的屈曲极限荷载和稳定性系数见表2,稳定性系数和开挖深度的关系曲线如图4(a)所示。
桩周土m=250 MN/m4,桩的边长为0.4 m,不同开挖深度的屈曲极限荷载和稳定性系数见表3,稳定性系数和开挖深度的关系曲线如图4(b)所示。
桩周土m=2.5 MN/m4,桩的边长为0.8 m,不同开挖深度的屈曲极限荷载和稳定性系数见表4,稳定性系数和开挖深度的关系曲线如图4(c)所示。
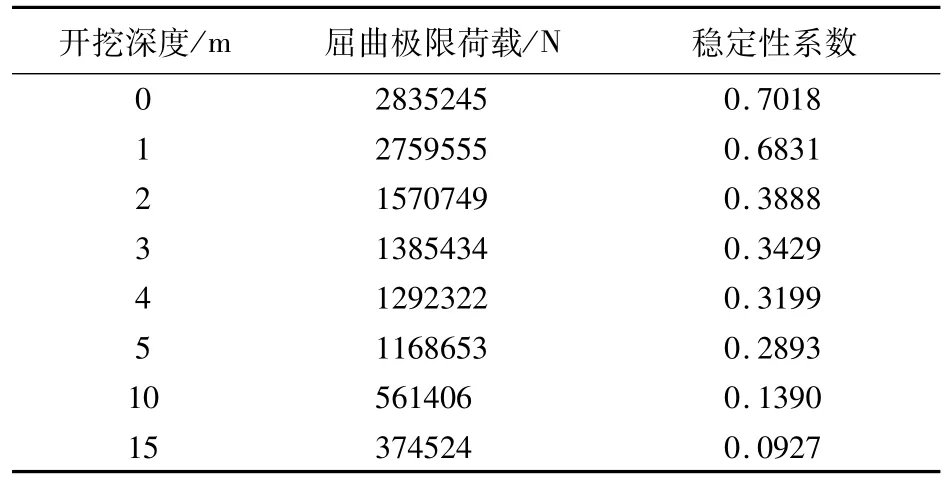
表2 不同开挖深度桩在m=2.5 MN/m4、b=0.4 m时的屈曲极限荷载和稳定性系数

表3 不同开挖深度桩在m=250 MN/m4、b=0.4 m时的屈曲极限荷载和稳定性系数
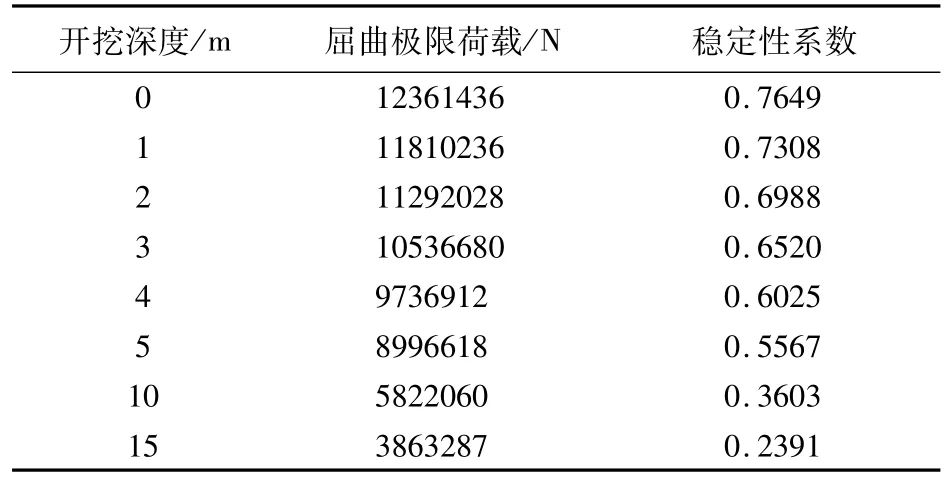
表4 不同开挖深度桩在m=2.5 MN/m4、b=0.8 m时的屈曲极限荷载和稳定性系数
从表2、3、4和图4可以看出:(1)在m值较大(密实砾砂、碎石土)的土中,桩周土未开挖时桩的稳定性系数接近1.0;而在m值较小(淤泥、饱和湿陷黄土)的土中,桩周土未开挖时桩的稳定性系数只有0.7。因此,在软土中即使桩周土不开挖也应考虑桩基的稳定性问题。(2)桩的边长和开挖深度相同的条件下,m值较大的桩周土中桩的稳定性系数偏大,这是因为m值大的桩周土对桩基的水平约束作用强,能有效减少其计算长度。(3)在桩周土质和开挖深度相同的条件下,截面边长大的桩基稳定性系数偏大,这是因为相同计算长度的桩基础,边长大的桩长细比较小。

图4 稳定性系数和开挖深度的关系曲线图(a)m=2.5 MN/m4、b=0.4 m;(b)m=250 MN/m4、b=0.4 m;(c)m=2.5 MN/m4、b=0.8 m
从图4(a)(b)可以看出,边长同为0.4 m的桩基础,虽然开挖前由于桩周土m值不同,稳定性系数有所差异,但开挖到15 m左右时稳定性系数均接近同一值(0.1)。这是由于开挖深度较小时,桩的计算长度(长细比)受桩周土m值的影响较明显;但随着开挖深度的增大,因开挖暴露出的桩身的自由长度占了更大比例,两者长细比更加接近,因此稳定性系数趋近于同一值。
2.2 具有一道或多道水平约束构件桩的屈曲极限荷载和稳定性系数
既有建筑桩基础桩顶多有承台、连系梁或底板相连,开挖桩周土并增设地下室后,也需要施工新的底板或承台等水平构件。水平构件对桩基础产生约束,能显著提高其受压稳定性。
桩周土m=2.5 MN/m4,桩的边长为0.4 m时,桩顶一道水平约束,桩周土开挖至10 m;桩周土开挖至5m,设置第二道支撑,继续开挖至10 m,两种工况下桩基础的屈曲极限荷载和稳定性系数随开挖深度变化规律见表5和如图5(a)所示。改变桩周土的m值(m=250 MN/m4),其他条件不变的情况下,两种工况下桩基础的屈曲极限荷载和稳定性系数随开挖深度变化规律见表6和如图5(b)所示。
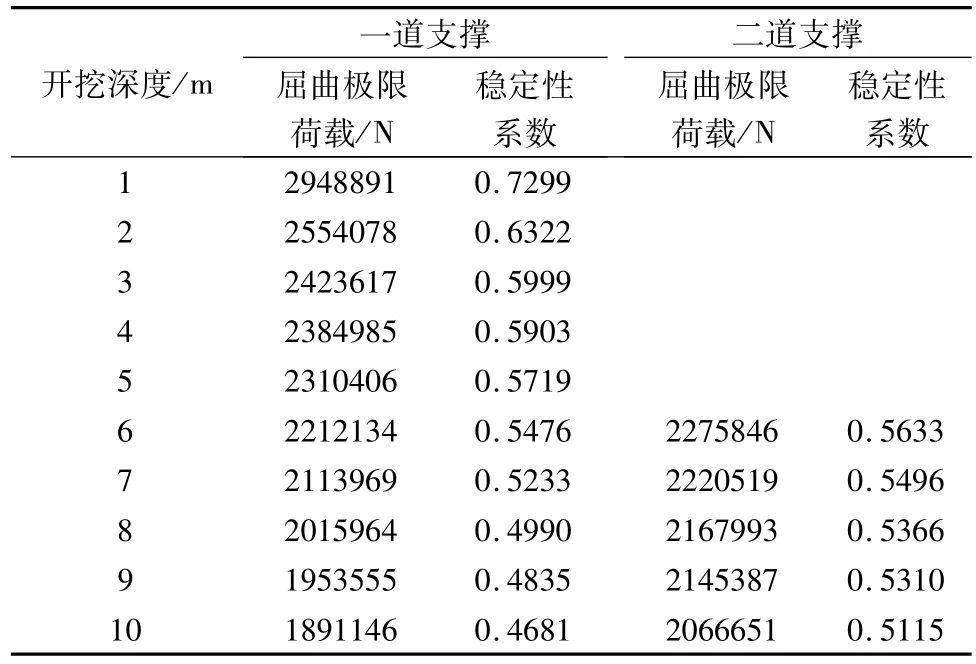
表5 增设支撑后不同开挖深度桩在m=2.50 MN/m4、b=0.4 m时的屈曲极限荷载和稳定性系数

图5 设置支撑后稳定性系数和开挖深度的关系曲线图(a)m=2.5 MN/m4、b=0.4 m;(b)m=250 MN/m4、b=0.4 m

表6 增设支撑后不同开挖深度桩在m=250MN/m4、b=0.4 m时的屈曲极限荷载和稳定性系数
通过比较表2、5和表3、6可知,增设水平约束构件后,桩基的稳定性系数提高1.2~2.9倍,桩周土开挖得越深、桩周土m值越小,增设水平约束构件的效果越明显。增设第二道支撑后,稳定系数有了进一步提高,但不如增设第一道桩顶支撑的效果明显。因此,利用桩基础为支撑开发地下空间,土方开挖后应及时施工底板等水平约束构件;特别是及时增设桩顶的水平支撑就更加重要。
2.3 桩基失稳时的屈曲变形
分析桩基失稳时的变形特性,可以获得桩基变形的挠曲线方程,为进一步分析桩基端部约束状态,确定桩基计算长度和长细比创造条件。
桩顶为自由端失稳时的屈曲变形图如图6所示,经数值分析可知,桩顶为自由端的桩基础,变形曲线大体为1/4周期正弦曲线的形态。桩周土开挖5 m后,在m值较小的淤泥、饱和湿陷黄土中,桩基失稳时的屈曲变形从桩顶延伸至开挖面以下3~4 m左右(如图6所示),再向下桩身无明显变形,此处可视为桩基础的“嵌固端”;而在m值较大的密实砾砂、碎石土中,桩周土对桩身约束能力强,“嵌固端”上移至开挖面处。
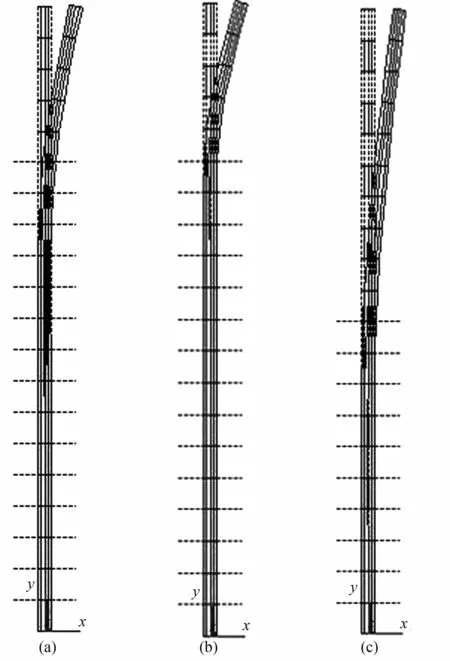
图6 桩顶为自由端失稳时的屈曲变形图
具有一道或多道水平约束构件桩的屈曲变形如图7所示。对于桩顶有一道水平约束构件的桩基础(m=2.5 MN/m4、b=10 m),其变形大体为半个周期的正弦曲线,如图7(a)所示。而桩顶有一道水平支撑构件、桩身中部增设一道水平支撑构件的桩基,失稳时桩身变形曲线为S形(如图7(b)所示)。水平支撑的位置是变形曲线的拐点。因此增设水平支撑,有效减小了桩身自由段的长度,从而减少了计算长度和长细比,提高了桩的受压稳定性。
3 结论
通过本研究可知:
(1)桩顶为自由端的桩基础,随着桩周土开挖深度的增加,其稳定性系数明显降低。相同开挖条件下,桩周土的m值越小,其桩基的稳定性系数越小;桩基截面边长越小,其稳定性系数越小。截面边长相同的桩基础,由于桩周土m值不同,开挖深度不大时稳定性系数有所差异(m值小的稳定性系数偏小),但随着开挖深度的增加,稳定性系数趋近同一值。

图7 具有一道或多道水平约束构件桩的屈曲变形图
(2)在相同开挖深度条件下,桩顶或桩身设置水平约束构件的桩基础比桩顶为自由端的桩基础稳定性系数提高1.2~2.9倍,开挖深度越深、桩周土m值越小,提高的效果越明显;增设桩顶支撑的效果将更加明显。
(3)m值较小的桩周土,桩基失稳时的变形曲线会延伸至开挖面一定深度;而m值较大的土,变形的影响深度较小。增设水平支撑后,有效减小了桩身自由段的长度,从而减少了计算长度、长细比,提高了受压稳定性。
(4)通过ANSYS二维建模和非线性数值分析,可以获得桩周土开挖条件下桩基础的受压极限荷载和变形特性。在分析桩周土开挖轴心受压桩稳定性的基础上,今后应继续深入研究偏心受压、有施工缺陷桩以及分层土的桩基稳定性,为既有建筑地下空间开发提供理论依据。
[1] 贾强,应惠清,张鑫.锚杆静压桩技术在既有建筑物增设地下空间中的应用[J].岩土力学,2009,30(7):2053-2057.
[2] JGJ 94—2008,建筑桩基技术规范[S].北京:中国建筑工业出版社,2008.
[3] Broms B.B..Precasting Piling Practice[M].London:Thomas Telford Ltd.,1981.
[4] 胡人礼.桥梁桩基础分析和设计[M].北京:中国铁道出版社,1987.
[5] 邹新军.基桩屈曲稳定分析的理论与试验研究[D].长沙:湖南大学,2005.
[6] Brandtzaeg A.,Harboe E..Bucking test of slender steel piles in soft guick clay[C].4 th International Conference on Soil and Mechanics Tehran,1957.
[7] Bergefelt A..The axial and lateral load bearing capacity and failure by bucking of piles in soft clay[C].4 th International Conference on Soil and Mechanics Tehran,1957.
[8] Lee K.L..Buckling of partially embedded piles in sand[J].Journal of Soil Mechanics and Foundation Division,1968,94(1): 255-270.
[9] 赵明华,王季柏.基桩计入摩阻力的屈曲分析[J].岩土工程学报,1996,18(3):87-90.
[10]赵明华.桥梁桩基的屈曲分析及试验[J].中国公路学报,1990,8(4):48-56.
[11]贾强,张鑫.板式基础托换法开发地下空间施工过程的数值分析[J].岩土力学,2010,31(6):1989-1994.
[12]王雅斋,梁新利.整体基础托换与地下加层施工工法[J].施工技术,2002,31(5):45-46.
[13]贾强,郑爱萍,张鑫.高承台钢管桩受压稳定性的试验研究和数值分析[J].岩土力学,2011,32(6):1736-1740.
[14]Zheng A.P.,Jia Q..Application of steel micro-piles in underpinning of existing buildings[C].12th International Conference on Inspection,Appraisal,Repairs&Maintenance of Structures(ICIARM),Singapore:Ci-premier Pte Ltd.,2010.
[15]周万清,姜德全.基于m法的高承台桩复合受力计算分析[J].路基工程,2010(5):41-43.
(责任编辑:吴芹)
Numerical analysis of plies bucking stability reducing caused by soil excavation around the piles
Jia Qiang1,2,Li Jiping1,2,Zhang Quanli3,et al.
(1.School of Civil Engineering,Shandong Jianzhu University,Jinan 250101,China;2.Shandong Provincial Key Laboratory of Appraisal and Retrofitting in Building Structures,Jinan 250013,China;3.Lushang Property Co.,Ltd.,Jinan 250014,China)
Pile underpinning technology is an effective method to develop underground space in retrofitting existing buildings.The soil excavation around the pile reduces the piles bucking stability.The 2D piles analysis model was established on ANSYS code,while the soil around the piles was simulated by spring element whose linear stiffness value gotten by m-method assumption.First,the superior limit of piles bucking stability was obtained by using characteristic value analysis.Then,according to nonlinear loading method,the accurate value of piles bucking stability and the deformation pattern of piles were obtained.Stability coefficient of top free piles obviously reduces while the soil around the piles excavated.According to same soil excavated depth,the pile has the lower value of stability coefficient in lower m value soil or shorter length of a side of piles.After the horizontal components installed on the piles,the stability coefficient of piles increases1.2-1.9 times than the top free piles,especially in lowerm value or deep excavated soil.
soil deep excavation;piles bucking stability;numerical analysis
TU 470
A
1673-7644(2014)06-0497-06
2014-07-03
国家自然科学基金项目(51278286);教育部创新团队项目(IRT13075)
贾强(1970-),男,副教授,博士,主要从事工程鉴定加固等方面的研究.E-mail:jiaqiang@sdjzu.edu.cn
