碎石桩复合地基非线性固结分析

高炳鑫,樊荣霞

(1.中国石化集团管道储运公司,江苏徐州 221008;2.南京瑞迪建设科技有限公司,江苏南京 210029)

碎石桩复合地基非线性固结分析

高炳鑫1,樊荣霞2

(1.中国石化集团管道储运公司,江苏徐州 221008;2.南京瑞迪建设科技有限公司,江苏南京 210029)

针对非线性偏微分固结方程难以直接求得解析解答的问题,采用对固结时间离散化的方法编制固结计算程序,在每个计算时间段内假设桩周土土体及碎石桩参数为常数,建立固结控制方程并求解。根据上一时间段的计算结果确定下一时间段的计算参数和初始条件,实现了同时考虑碎石桩和软土非线性特征的复合地基固结计算。在此基础上,分析了复合地基的固结性状,得出碎石桩复合地基随着Cc/Ck增大其固结速率变慢的结论。

复合地基;非线性偏微分方程;地基固结;碎石桩

软土的渗透系数较低,但压缩性很大,因此在软土地基上修建工程时,沉降量以及沉降速率难以控制。碎石桩由于其桩身模量和渗透系数较大,能够有效减少地基沉降并加快固结速率,因此被广泛应用于软土地基处理中[1-4]。

对于碎石桩复合地基的固结问题,求解时通常假设桩周土渗透系数kh、压缩模量Es以及碎石桩压缩模量Ec为常数。如邢皓枫等[5]在忽略施工引起的涂抹区影响的基础上,根据排水量与体积应变相等的条件,给出一种碎石桩复合地基简化方程;Xie等[6]考虑了桩体固结以及涂抹区渗透系数的3种变化规律,推导了碎石桩复合地基的计算方程;王瑞春等[7]以碎石桩完全排水为前提,根据正交性条件给出了双层碎石桩地基的固结解答;张玉国等[8]在进行碎石桩复合地基求解时,将模型的顶面和底面假设为半透水边界,即考虑了固结模型边界的渗透阻力。虽然这些关于碎石桩复合地基固结研究成果各自的侧重点不同,但都是在桩土压缩模量以及渗透系数均为常数的基础上开展的。而Tavenas等[9]的研究表明,软土的压缩性和渗透性随着孔隙比的变化呈现出非线性的特点;朱志铎等[10]的研究结果也表明,碎石桩的压缩模量是与施加应力有关的指数函数,亦呈现出非线性的特点。随着固结过程的发展,土体和桩体的孔隙比及有效应力不断变化,因此渗透性和压缩性必然是非线性的。如果将土体和碎石桩参数认为是常数,必然会引起固结计算结果的偏差。

到目前为止,关于复合地基的非线性固结理论研究较少,主要成果有:Indraratna等[11]采用半对数模型给出了瞬时加载情况下考虑涂抹区影响和土体应力历史的砂井径向固结解。但由于砂井的压缩模量与软土相近,因此砂井地基没有应力集中效应,从而有别于碎石桩复合地基。卢萌盟[12]在假设桩体压缩模量和桩周土压缩模量同步变化的基础上考虑了应力集中效应和涂抹区的影响,给出了瞬时加载情况下碎石桩复合地基径向固结解。但需要注意的是,文献[11-12]中列出的非线性偏微分固结方程很难直接得到解析解,因此对khEs做了平均化假设,以便于求解。实际中,碎石桩和软土的渗透系数及压缩模量在固结过程中是不断变化的,并不能简单地用平均化假设进行处理。

本文同时考虑了碎石桩和软土的非线性,采用对固结时间离散化的方法,在每个计算时间段内假设桩周土及碎石桩参数为常数,利用上一步的计算结果推算下一时间段内桩体和桩周土的计算参数,以及固结方程的初始条件,从而实现同时考虑碎石桩和软土非线性特点的固结计算。

1 数学模型

1.1 计算简图

图1为碎石桩复合地基计算简图,q为瞬时施加的垂直于影响区域的均布荷载。图中rc、rs、re分别为桩体、扰动区和影响区域半径,ks、kh分别为扰动区和非扰动区的渗透系数。模型周边为不透水边界。

图1 复合地基计算简图Fig.1 Calculation diagram of composite ground

1.2 基本假定

根据已有研究成果,做出如下假设:

a.桩土间的等应变条件成立,复合地基中桩和桩周土完全饱和,且渗流符合Darcy定律。

b.碎石桩复合地基中桩周土主要通过径向渗流向碎石桩排水实现固结,因此对于桩周土仅考虑径向渗流,外荷载瞬时施加[11]。

c.碎石桩的渗透系数较高,认为桩体完全透水,即不考虑桩阻作用。

d.扰动区ks为常数,其他性质与未扰动区相同。

e.桩周土的压缩性和渗透性随孔隙比的减小而减小,符合对数函数关系,即

式中:e——软土孔隙比;e0——软土的初始孔隙比;Ck、Cc——软土的渗透指数和压缩指数;kh,i、σs,i——软土的初始渗透系数和初始竖向有效应力;σs——软土竖向有效应力。

f.碎石桩的压缩模量变化规律为

式中:Pa——大气压(一般取100 kPa);f——试验参数;km——桩体的渗透系数;σc——均布荷载在桩体中任一深度产生的有效应力。

1.3 控制方程

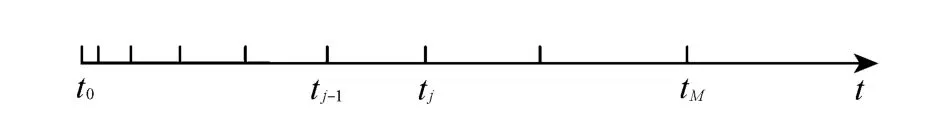
图2 固结时间划分Fig.2 Division of consolidation time

在整个固结过程中,复合地基的参数是随着超静孔隙水压力的消散而不断变化的,控制方程是关于超静孔隙水压力的非线性偏微分方程,难以求得解析解。现将固结时间划分为M段(图2),由于在各时间段内超静孔隙水压力变化有限,因此可以假设每个时间段内复合地基的参数为常数。在复合地基固结过程中,初始时间段超静孔隙水压力变化剧烈,随着时间的增长变化趋势逐渐变缓。因此在初始阶段时间间隔划分较密,随着固结的进行,时间间隔逐渐增大。

在任意时间段[tj,tj+1](0≤j≤M-1)内,推导碎石桩复合地基的固结控制方程。

对于碎石桩复合地基,由竖向平衡条件以及等应变条件可得

参照文献[3,13],可得土体径向固结方程:

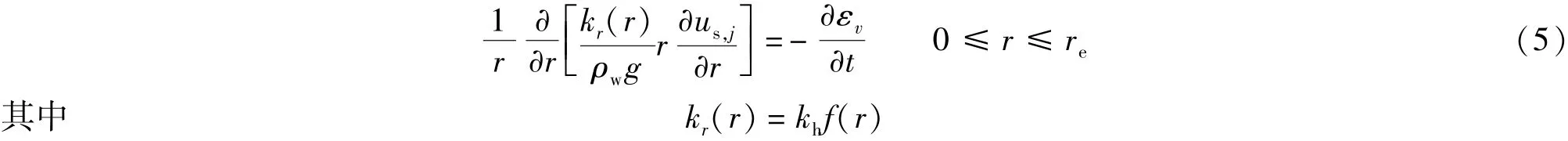
式中:ρw——孔隙水密度;g——重力加速度;εv——体积应变。根据本文假设,rc≤r≤rs时f(r)=ks/kh,rs≤r≤re时f(r)=1。

求解条件为

式(5)两边对r积分2次,利用边界条件(6)和(7)可得

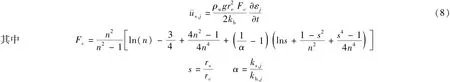
式中:εj——[tj,tj+1]时间段内的体积应变。

将式(8)代入式(4)可得

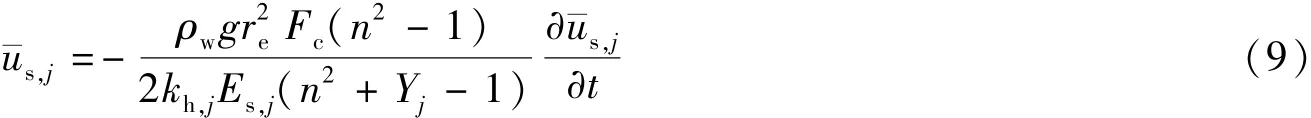
式(9)即为本文的固结控制方程。

1.4 方程求解

结合初始条件式(10),对于方程(9)求解可得

2 求解思路

利用MATLAB软件编写求解程序,基本编写思路如下:

a.输入复合地基基本参数,包括σ0、rc、、rs、re、ρw,桩体和桩周土的初始压缩模量Ec,0和Es,0,扰动区和非扰动区的初始渗透系数ks,0和kh,0,碎石桩参数Pa、km和f,土体和桩体的初始有效应力(即自重)σs,i和σc,i。

b.在每个时间段内建立固结控制方程,根据初始条件对方程进行求解,得到t1时刻土体中的平均超静孔隙水压力和有效应力(t1)、(t1),碎石桩的有效应力(t1)。

c.根据计算所得的有效应力计算得到t1时刻土体的压缩模量、渗透系数及碎石桩的压缩模量。将土体和碎石桩参数代入固结方程,并将(t1)作为初始条件,开始[t1,t2]时间段的固结计算。

d.重复(b)～(c)步,即可进行后续各时间段内的固结计算。以(tj)作为控制条件,当(tj)＜0.1 kPa时,判断程序结束。

3 结果验证及固结性状计算

假设某碎石桩复合地基的基本参数为:re=1.5 m,rc=0.5 m,σ0=100 kPa,ks/kh=0.1,rs/rc=2,kh,0= 0.0002 m/d,e0=1.0,ρw=1000 kg/m3,碎石桩桩长H=10 m。

3.1 结果验证

我国软土的Cc一般在0.35～0.75的范围内[14];Cc/Ck的取值范围为0.5～2.0[15]。假设软土和碎石桩的ρs=1650kg/m3和ρc=2100kg/m3,则软土和碎石桩的平均初始竖向应力(0.5ρgH)分别为82.5kPa和105kPa。

本文计算中固结计算时间共取250 d,划分为M=20个时间段。为证明本文计算程序的正确性,将计算条件取为与文献[8]相同。文献[8]假设在整个固结过程中桩土压缩模量比Y不变,对khEs做了平均化假设,因此,本文取Y=15。文献[15]的研究表明,碎石桩复合地基的桩土压缩模量比一般为10～20;并令khEs在整个固结计算过程中等于(kh,1Es,1+kh,MEs,M)/2。固结完成时超静孔隙水压力为0 kPa,计算得出此时的附加竖向有效应力为32.1 kPa,则整体竖向应力为114.6 kPa。将竖向应力值代入式(1)和式(2),即可计算得到kh,1、Es,1、kh,M以及Es,M。

在相同假设条件前提下,本文计算结果与文献[8]的计算结果吻合,如图3所示,说明本文采用对时间离散化的方法求解固结控制方程的程序是正确可行的。

3.2 固结性状计算分析

对于碎石桩,根据文献[10]的结果,取其参数为Pa=100 kPa,km=412,f=0.27;对于桩周土体,采用本文提出的时间离散化方法进行碎石桩复合地基非线性固结计算。

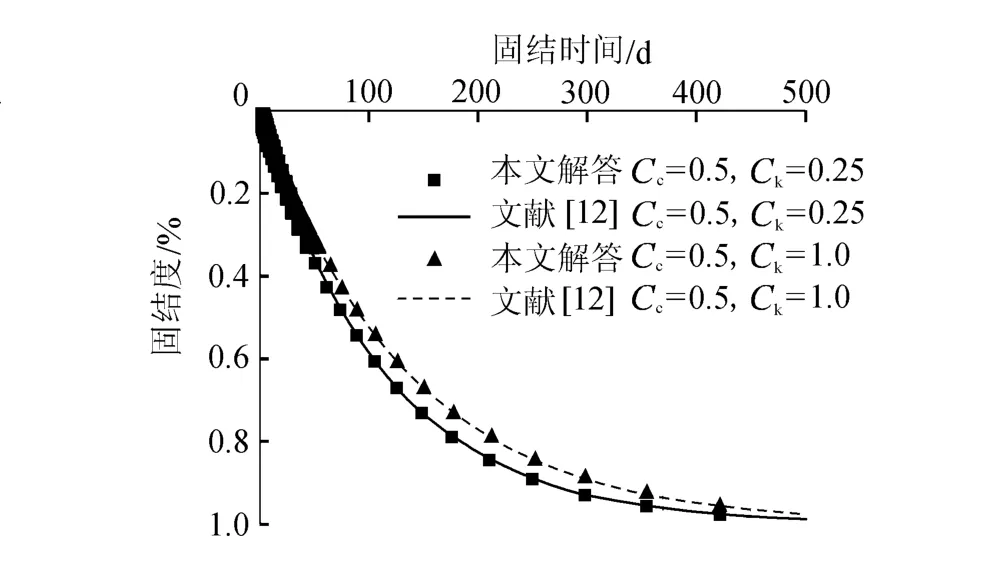
图3 本文计算程序验证Fig.3 Verification of accuracy of program in this paper

图4 Cc和Ck对固结速率的影响Fig.4 Influences of Ccand Ckon consolidation rate

图5 固结系数随时间变化规律Fig.5 Variation of consolidation coefficient with time

如图4所示,随着Cc/Ck的增大,碎石桩复合地基的固结速率变慢。分析其原因,碎石桩复合地基的固结速率与土体的固结系数有关,固结系数越大,固结速率越快。而土体的固结系数又由土体压缩模量以及渗透系数组成。随着固结过程的发展,土体的孔隙比减小,因此土体压缩模量增大,渗透系数减小。土体压缩模量的增大使固结系数增大,渗透系数减小又使固结系数减小,所以在固结过程中土体压缩模量和渗透系数的变化对于渗透系数的影响是相反的。随着Cc/Ck数值的增大,固结过程中软土压缩模量的增大速率减小,而渗透系数的减小速率增大,因此软土压缩模量增大对于渗透系数的影响占优,如图5所示。Cc/Ck=1是分界线:当Cc/Ck＞1时,随着固结时间增加,土体固结系数减小;当Cc/Ck＜1时,随着固结时间增加,土体固结系数增大。

在整个固结过程中,桩土模量比不断增加,即碎石桩桩体的压缩模量不断增加,如图6所示。如果将桩土模量比假设为常数进行计算,可能会使固结度计算产生偏差。土体的压缩模量与Cc有关,Cc越大,土体压缩模量越小。如图7所示,随着土体压缩指数的增加(即土体压缩模量减小),碎石桩复合地基的固结速率减慢。

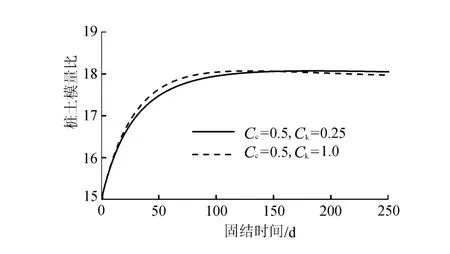
图6 桩土压缩模量比随时间变化规律Fig.6 Variation of pile-soil modular ratio with time

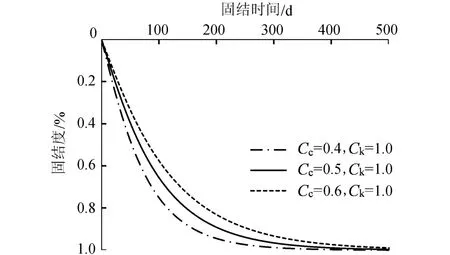
图7 土体压缩指数对固结速率的影响Fig.7 Influence of Ccon consolidation rate

4 结 论

采用对时间离散化的方法,在每个时间段内将软土和碎石桩参数假设为常数,建立固结方程并求解。根据求解结果,确定下一时间段内的软土和碎石桩参数以及初始条件,实现了同时考虑碎石桩和软土非线性特点的复合地基固结分析。

a.随着Cc/Ck的增大,碎石桩复合地基的固结速率变慢。

b.当Cc/Ck＞1时,随着固结时间增加,土体固结系数减小;当Cc/Ck＜1时,随着固结时间增加,土体固结系数增大。

c.在整个固结过程中,桩土模量比不断增加。如果将桩土模量比假设为常数进行计算,可能会使固结度计算产生偏差。

[1]张福海,王保田,王炳奇,等.大粒径碎石桩在饱和超软土地基中的应用[J].河海大学学报:自然科学版,2006,34(4): 430-434.(ZHANG Fuhai,WANG Baotian,WANG Bingqi,et al.Application of large grain-size gravel piles to strengthening saturated super-soft ground[J].Journal of Hohai Unversity:Natural Sciences,2006,34(4):430-434.(in Chinese))

[2]王保田,唐劲柏.强夯碎石桩的发展及成桩机理分析[J].河海大学学报:自然科学版,1999,27(6):30-34.(WANG Baotian,TANG Jingbo.Development of DRM and analysis of column-rormation mechanism[J].Journal of Hohai Unversity: Natural Sciences,1999,27(6):30-34.(in Chinese))

[3]谢康和,曾国熙.等应变条件下的砂井地基固结解析理论[J].岩土工程学报,1989,11(2):3-7.(XIE Kanghe,ZENG Guoxi.Equal strain consolidation of vertical drain foundation[J].Chinese Journal of Geotechnical Engineering,1989,11(2): 3-7.(in Chinese))

[4]HAN Jie,YE Shulin.Simplified method for consolidation rate of stone column reinforced foundations[J].Journal of Gotechnical and Geoenvironmental Engineering,2001,127(7):597-603.

[5]邢皓枫,龚晓南,杨晓军.碎石桩复合地基固结简化分析[J].岩土工程学报,2005,27(5):521-524.(XING Haofeng, GONG Xiaonan,YANG Xiaojun.Simplified analysis for consolidation of gravel-pile composite foundation[J].Chinese Journal of Geotechnical Engineering,2005,27(5):521-524.(in Chinese))

[6]XIE Kanghe,LU Mengmeng,LIU Ganbin.Equal strain consolidation for stone columns reinforced foundation[J].International Journal for Numerical and Analytical Methods in Geomechanics,2009,33:1721-1735.

[7]王瑞春,谢康和.双层散粒体材料桩复合地基固结解析理论[J].岩土工程学报,2001,23(4):418-422.(WANG Ruichun, XIE Kanghe.Analytical theory for consolidation of double-layered composite ground with granular columns[J].Chinese Journal of Geotechnical Engineering,2001,23(4):418-422.(in Chinese))

[8]张玉国,谢康和,应宏伟,等.双面半透水边界的散体材料桩复合地基固结分析[J].岩土工程学报,2005,27(3):304-307.(ZHANG Yuguo,XIE Kanghe,YING Hongwei,et al.Consolidation analysis of composite foundation of granular columns with impeded boundaries[J].Chinese Journal of Geotechnical Engineering,2005,27(3):304-307.(in Chinese))

[9]TAVENAS P,JEAN P,LEBLOND P,et al.The permeability of natural soft clays.Part II:Permeability characteristics[J].Canadian Geotechnical Journal,1983,20:645-659.

[10]朱志铎,刘义怀.碎石变形特征及挤密碎石桩复合地基效果评价[J].岩土力学,2006,27(7):1153-1157.(ZHU Zhiduo, LIU Yihuai.Deformation characteristics of broken stone and effect evaluation of composite foundation with stone compaction column[J].Rock Soil Mech,2006,27(7):1153-1157.(in Chinese))

[11]INDRARATNA B,RUJIKIATKAMJORN C,SATHANANTHAN I.Radial consolidatin of clay using compressibility indices and varying horizontal permeability[J].Canadian Geotechnical Journal,2005,42:1330-1341.

[12]卢萌盟.复杂条件下复合地基固结解析理论研究[D].杭州:浙江大学,2009.

[13]WANG Xusheng,JIAO Jiujiu.Analysis of soil consolidation by vertical drains with double porosity model[J].International Journal for Numerical and Analytical Methods in Geomechanics,2004,28(14):1385-1400.

[14]戢英.软土地基处理技术及在公路施工中的应用[D].天津:天津大学,2006.

[15]BERRY P L,WIKISON W B.The radial consolidation of clay soils[J].Geotechnique,1969,19(2):253-284.

Nonlinear consolidation analysis of stone column composite ground

GAO Bingxin1,FAN Rongxia2
(1.Sinopec Pipeline Storage and Transportation Company,Xuzhou 221008,China; 2.Nanjing R&D Tech Group Co.,Ltd.,Nanjing 210029,China)

It is difficult to obtain the analytical solution of a nonlinear consolidation partial differential equation.In order to solve this problem,the consolidation time is segmented into small intervals and the parameters of soft soil and stone columns are assumed to be constants at any time interval.Then,the governing consolidation equation of the stone column composite foundation is built and solved at each time interval.The calculation parameters and initial conditions of the computing unit can be determined by the calculation results of a previous time interval.Finally,consolidation calculation is conducted for the composite ground,with consideration of the nonlinear characteristics of the stone column and soft soil.On this basis,the nonlinear consolidation properties of composite ground are analyzed.The results show that the consolidation rate of the stone column composite ground decreases with the increase ofCc/Ck.

composite foundation;nonlinear partial differential equation;foundation consolidation;stone column

TU46

:A

:1000-1980(2014)06-0518-06

10.3876/j.issn.1000-1980.2014.06.010

2013-11 21

高炳鑫(1955—),男,浙江绍兴人,高级工程师,主要从事地基基础研究。E-mail:lanshanxmb@126.com