矢量地形图要素边线直角化方法研究
2014-07-02应国伟侯华斌
应国伟,侯华斌,刘 江,吴 思
(四川省第三测绘工程院,四川 成都 610500)
矢量地形图要素边线直角化方法研究
应国伟,侯华斌,刘 江,吴 思
(四川省第三测绘工程院,四川 成都 610500)
针对矢量地形图数据中要素边线直角化问题,分析了最小二乘法的优缺点,提出了一种新的解决方案——边线中点固定算法,该方法的优势在于算法模型简洁、运算速度快,适用于大数据量的处理和运算。本文详细描述了该解决方案的实现过程,并分析了其存在的不足和适用范围。
ArcGIS;地形图;直角化;最小二乘法
一、引 言
数字地形图按其数据采集方法的不同可分为全野外数字化测图、摄影测量数字化测图和扫描矢量化测图[1]。但无论哪种方法都会无可避免地遇到一个问题:实际为矩形的要素,特别是建筑物要素,采集到地形图上时并不是规则的矩形,而是接近矩形,本文称之为伪矩形。而如何在精度许可的范围内对这些伪矩形进行直角化处理,是本文探讨的问题。
二、伪矩形产生的原因和表现
伪矩形产生的原因一般是由扫描纠正误差、测量误差、立体测图误差等方面引起的。其表现形式是DLG图形线划发生变形和扭曲,图形的内角与多边形的实际直角存在差异[2],如图1所示。
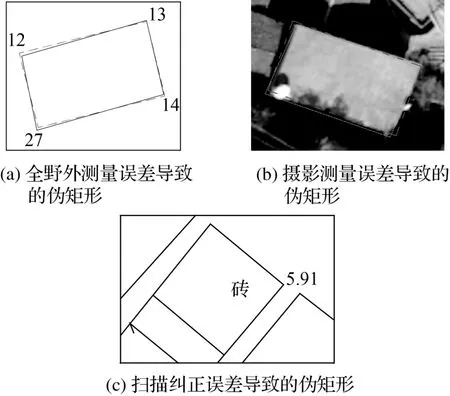
图1 伪矩形产生原因
三、直角化的方法
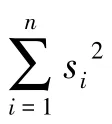
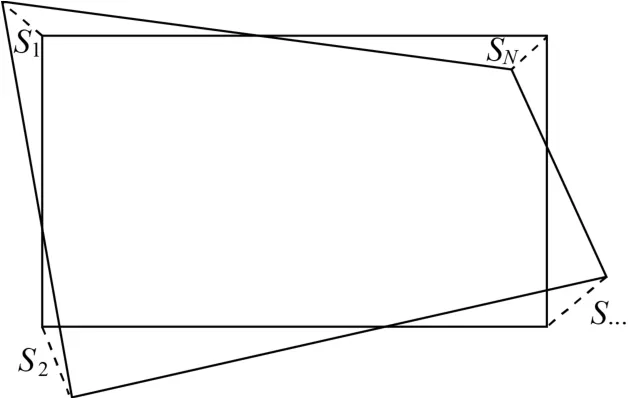
图2 伪矩形直角化
1.最小二乘法算法

最小二乘法算法的优点是技术优化、结果可靠,缺点是当房屋边线比较多时,则增加递归运算负荷,程序编制难度也较大;而且最小二乘法只考虑图形结果的最优符合性,并不考虑图形的实际真实性。如图3所示,实线为矢量采集的建筑物边线,虚线为经过最小二乘法优化的建筑物边线,把图3的A处放大(如图4所示)可以看出,经优化后的边线已经完全偏离了实际边线。

图3 最小二乘法直角化结果

图4 最小二乘法直角化结果(放大图)
因此,笔者提出了另外一种新的算法,并称之为边线中点固定算法。
2.边线中点固定算法
相对最小二乘法算法是一种绝对算法来说,边线中点固定算法是一种近似算法。如图5所示,设虚线为正交后的矩形,其边A′B′的方位角为β,它必须经过边AB的中点MAB且与经过BD中点的方位角为(β+π/2)的B′D′相交于B′,依此类推,直到遍历完成所有的边为止。这样,既保证了直角化后图形的整体性,又达到了笔者的目的。
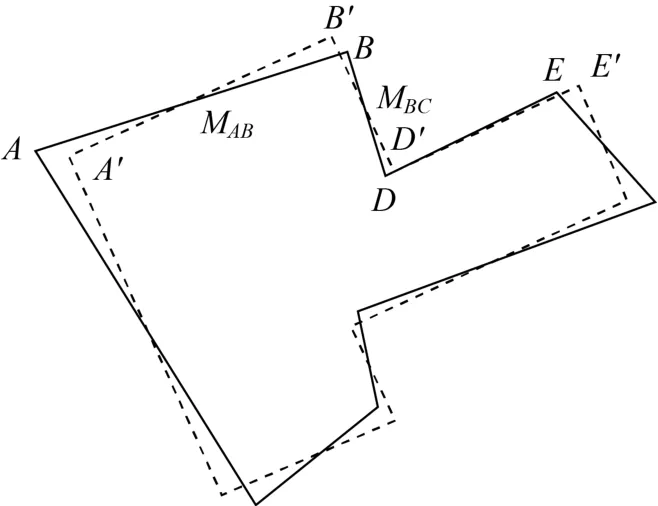
图5 边线中点固定算法模型图解
四、编程实现思路
1)如图6所示,设要素起点从1开始,共10个节点,形成闭合图形。
2)首先,获得要素边线的坐标串,即拐点1~10的坐标,并整理为坐标数组,再计算图形各边的平均方位角,其目的是为了获得初始边(第1条边)L12的改正边L1′2′的方位角。
3)获得初始边L12的初始方位角后,从L12中点M12起,以任意长度确定一条直线M12K。
4)求第2条边L23中点M23到直线M12K的垂足点,此点即为节点2的改正点2′。
5)以2′与第2条边L23中点M23确定直线,求第3条边L34中点M34到直线M122′的垂足点,此点即为节点3的改正点3′。
6)依次求出所有节点的改正坐标。

图6 边线中点固定算法编程图解
本文以Esri Geodatabase DLG数据格式(∗.mdb)为例,实现边线中点固定算法模型在ArcGIS环境下ArcObject的代码编写,笔者使用的ArcGIS版本为10.0,开发环境为Microsoft Visual Studio 2010,开发语言为Visual Basic。经实践证实,此算法代码简洁,运行速度快,效果良好,并保证了图形要素的实际真实性。图7为采用边线中点固定算法纠正后与图4的对比效果(虚线为改正后边线),很显然,图7更符合实际情况。

图7 边线中点固定算法结果实例
五、误差分析和精度控制
无论采取哪种算法,若不设定条件,程序都会无条件地将伪矩形直角化为标准矩形,而不考虑直角化变形,但对地形图编辑而言这是不允许的。因此,在进行房屋直角化时,还必须考虑误差控制或限制,可设定中误差和残差值进行约束,也可设定角度或拐点位移距离阈值,当超过这一阈值时,程序退出运行并作出提示。
六、结束语
本文中,笔者提出了最小二乘法算法以外的一种新的地形图要素边线直角化解决方案,经实际应用证明,该方法可较大程度减少程序运算量,并最大限度地保证了图形的实际符合性,具有较好的应用价值。
[1] 叶锦强,葛山运.基于条件平差的数字地图中地物直角纠正方法[J].测绘,2011,34(4):165-167.
[2] 王立新,朱伟.基于ArcGIS的1∶5万DLG数据库生成地形图的设计与实现[J].测绘通报,2008(5):58-61.
[3] 王辉连,武芳,张琳琳,等.数学形态学和模式识别在建筑物多边形化简中的应用[J].测绘学报,2005,34 (3):269-276.
[4] 童小华,华慧,杨光,等.面向对象数字化和数据处理[J].测绘通报,1998(5):33-35.
[5] 王娜,高源鸿,肖志婷.数字化地形图对象的几何约束和平差[J].测绘与空间地理信息,2008,31(6):193-195.
[6] 张宏.测量平差中最小二乘法的数学原理及简例[J].西部探矿工程,2007(2):83-84.
[7] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2009.
[8] 童小华,熊国锋.建筑物多边形的多尺度合并化简与平差处理[J].同济大学学报:自然科学版,2007,35 (6):207-208.
[9] 刘鹏程,艾廷华,邓吉芳.基于最小二乘的建筑物多边形的化简与直角化[J].中国矿业大学学报,2008,37(5):700-704.
[10] 刘鹏程,艾廷华,胡晋山.一种基于条件极值的建筑多边形直角化的方法[J].测绘与空间地理信息,2008,31(5):12-14.
Right Angle Method of Edge Elements in Vector Topographic Map
YING Guowei,HOU Huabin,LIU Jiang,WU Si
P217
B
0494-0911(2014)12-0112-02
应国伟,侯华斌,刘江,等.矢量地形图要素边线直角化方法研究[J].测绘通报,2014(12):112-113.
10.13474/j.cnki.11-2246. 2014.0412
2013-11-06
数字制图与国土信息应用工程国家测绘地理信息局重点实验室开放研究基金(GCwd201209);测绘地理信息公益性行业科研专项经费(201412010);四川省测绘地理信息局科技计划(J2013SZ06)
应国伟(1972—),男,四川筠连人,高级工程师,研究方向为地理信息系统。
