基于概率排序的存储约束树形搜索算法的研究

朱瑞鑫，金小萍，冯会真

(中国计量学院信息工程学院，浙江杭州310018)

基于概率排序的存储约束树形搜索算法的研究

朱瑞鑫，金小萍，冯会真

(中国计量学院信息工程学院，浙江杭州310018)

鉴于目前MIMO系统中大多数多符号差分检测算法对于大容量存储空间的需求和高计算复杂度的缺点，提出了一种概率排序的存储约束树搜索(Probabilistic Sorting Memory Constrained Tree Search，PSMCTS)算法，利用概率排序的性能优势与MCTS的存储优势来解决此问题。经过理论分析与仿真验证，该算法能够继承MCTS算法的优势，能够动态地适应预设的存储空间，适合硬件实现，而排序算法提高了检测性能，在固定的存储需求下，性能表现更加逼近ML算法，同时能够解决MCTS算法在小存储容量条件下低信噪比区域计算复杂度仍比较高的问题。因此，PSMCTS可以作为一种有效的方案应用在通信系统中。

MIMO;概率排序;存储约束属性搜索

目前，大多的多符号差分检测算法［1］是基于树形检测，而ML检测［2］是一种BER性能最优的检测算法，但穷搜索使得复杂度与分组长度和天线数等均呈指数关系，从而导致它根本无法在实际中运用。因而一些低复杂度的检测算法相继被提出来解决这个关键难题［3-8］。大体有3种搜索策略:深度优先、宽度优先和度量值优先。球形译码就是典型的以深度优先搜索策略为主的检测算法［3-4］，这种算法由于不断地回溯导致在不同的信道环境下具有不同的吞吐量，且并行和流水线操作困难。宽度优先搜索策略［5］，如K-Best算法，具有高吞吐量和稳定的复杂度，并且适于流水硬件实现，但是由于K值的约束会带来一定的性能损失。而以度量值优先搜索策略为主的Stack算法［6］，又叫Dijkstra's算法［7-8］，它总是扩展列表中度量值最小的节点，这种策略是众多搜索策略中访问节点最少的。

这些算法的硬件需求通常较大，计算复杂度较高，而硬件的固定存储空间会限制了其性能。MCTS算法［9］能够在任意给定的存储空间约束条件下，逼近最大似然检测的性能，同时能够降低计算复杂度。但该算法在较小存储空间的限制下，复杂度依然很大。DSPS(Dijkstra’s Search with Probabilistic Sorting)算法［10-11］是由Ronald Y.Chang等人提出的一种新的树搜索算法，利用数学统计概率来进行对节点度量值的比较，相比穷搜索的传统Dijkstra’s算法，大大降低了所需访问的节点数，并且有效地提高了性能表现，在节省存储空间和降低复杂度方面有着很高的研究价值。本文综合以上问题，提出一种新的存储约束搜索算法——PSMCTS，利用DSPS算法判决准确度高以及搜索访问点数少的优势，优化MCTS算法的存储循环策略，降低了对存储空间的需求，同时提升了系统性能。

1 系统模型

文中采用MIMO多天线系统，接收与发送天线数目分别为NR=1和NT=2，系统框图如图1所示，其中译码器部分就是本文的研究重点。

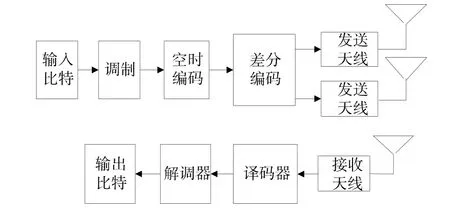
图1 MIMO系统框图

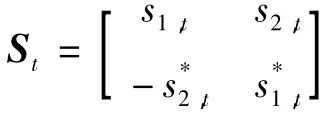
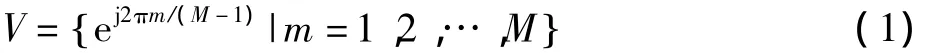
St满足St=I2。为了进行差分编码，需设定一个参考矩阵C0，该矩阵不携带任何数据信息。令C0=，数据进行空时编码之后进入差分编码器，其编码方式为

式中:Ct表示差分编码矩阵。

进行差分编码之后，系统通过空时天线矩阵，采用不同的多径信道模型进行发送。设某时刻t的接收信号为

假设多符号差分检测的观察窗口长度为N，即在多符号差分检测系统中，接收机连续接收N个符号来检测。传统度量值判决式为

2 PSMCTS算法

在MCTS算法中，采用式(4)的度量值判决，被访问节点的选择总是受限于存储空间和度量值，它总是先访问不超过存储空间需求的度量值最小的节点，使得MCTS算法的搜索策略取决于预设的存储空间大小。存储需求对于硬件实现来说是一个很重要的因素，需求越小越容易实现。在小存储空间条件下，MCTS趋向于深度优先搜索策略，即趋向于深度优先球形译码算法，仍然需要大量的回溯访问，计算复杂度依然相对较大。

本文利用文献［10］中的思想，针对式(4)进行优化，将其转化为利用数学统计概率密度来进行度量的判决式为

利用Dijkstra’s算法特点，基于MCTS步骤［9］进行改进，得出PSMCTS的搜索步骤如下:

1)根据系统要求设置发送、接收天线数目NR和NT、调制星座点数L等参数，初始化可用存储空间M，M≥(N-1)(L-1)+1。初始化多符号窗口长度N，将分组长度为N的接收信号输入到PSMCTS检测器中。

2)设树的层数变量K=N，表示从树根(对应的度量值为0)开始，如果K≠2，扩展根节点到L个子节点，然后把这L个子节点存入列表，按照式(5)通过转化的判决度量式来进行MCTS算法思想的搜索过程。

(2)由上层的最佳节点进行拓展，得到L个拓展的子节点，并存入存储空间中。在低存储空间的情况下，可预存分支节点数，直接选择拓展子节点的最佳分支，进行下一层的搜索;如果K=1，直接输出最小值。如果存储空间足够，可保留多层的分支节点度量值，将最佳子节点的拓展分支加入到空间，在存储空间集合中进行堆栈算法，重复以上步骤进行回溯运算，重复此步骤，直到寻找出本层的最佳子节点，以此为根节点进行拓展至下一层的搜索;如果K=1，直接输出最小值。

(3)重复以上搜索步骤，直至搜索到最底层，并输出最佳路径值。

3)如果K=2，那么找到一个该访问节点下的最佳叶子节点，并用其替换列表中的访问节点，然后根据列表中最佳的叶子节点进行更新列表，输出最佳路径。

PSMCTS和MCTS算法的节点搜索演示分别如图2、图3所示。

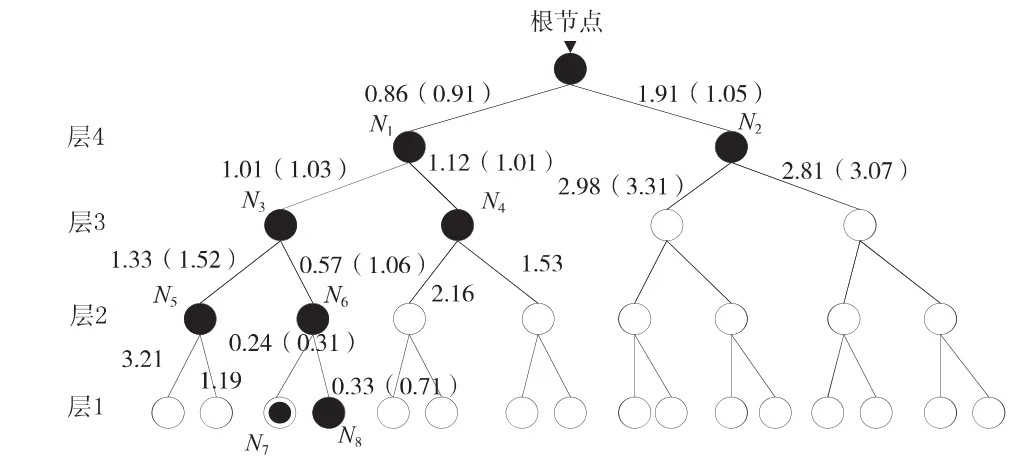
图2 PSMCTS树形节点分析图

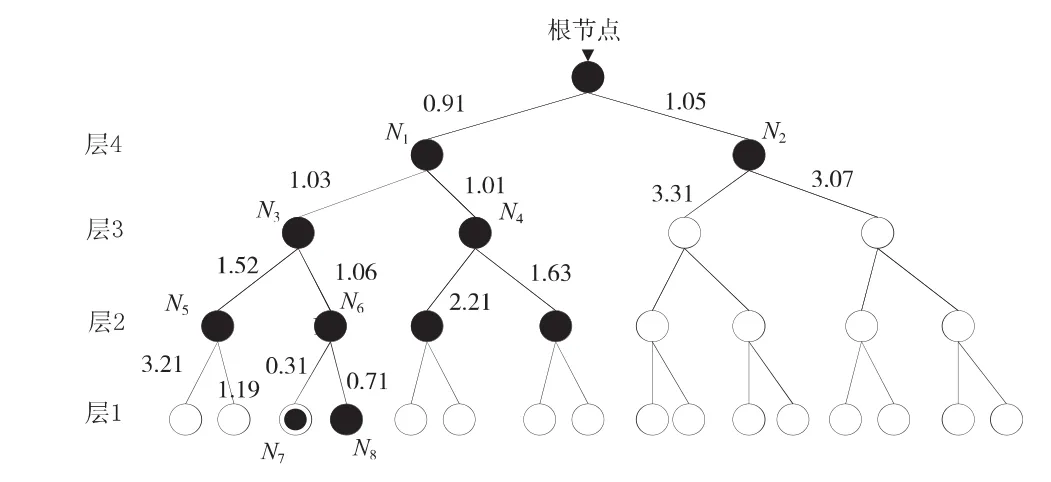
图3 MCTS树形节点分析图

图中，表示未访问的节点 ，表示访问节点 ，表示最佳节点。图2为PSMCTS树形节点分析图，其中数值为概率度量值，括号内为传统度量值。当迭代运算至N3节点进行拓展后，此时存储的点为N2，N4，N5，N6。传统度量值的排序为N2，N6，N4，N5，会选择N2为最佳节点进行返溯，但是按照本文算法度量值的排序为N6，N4，N5，N2，会直接选择N6为最佳节点进行下一轮的迭代并进行拓展，大大减少了搜索的节点访问数。图3为MCTS树形节点分析图，图中数值为传统度量值，通过对比可以直观地表现出PSMCTS算法访问节点数少的优势。另外，为了更加直观地体现出搜索过程的优势，表1和表2分别列出了PSMCTS与MCTS算法的具体搜索存储状态，其中黑体表示选择拓展的访问节点。

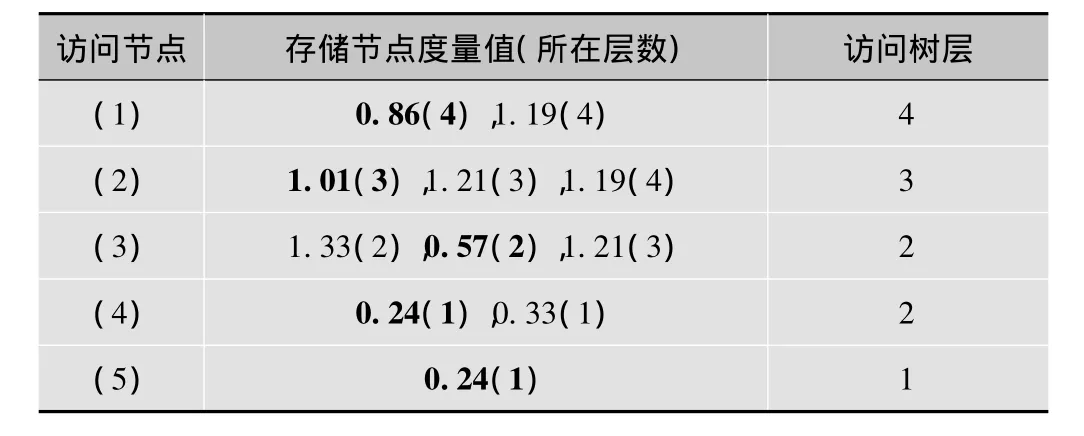
表1 PSMCTS搜索状态表

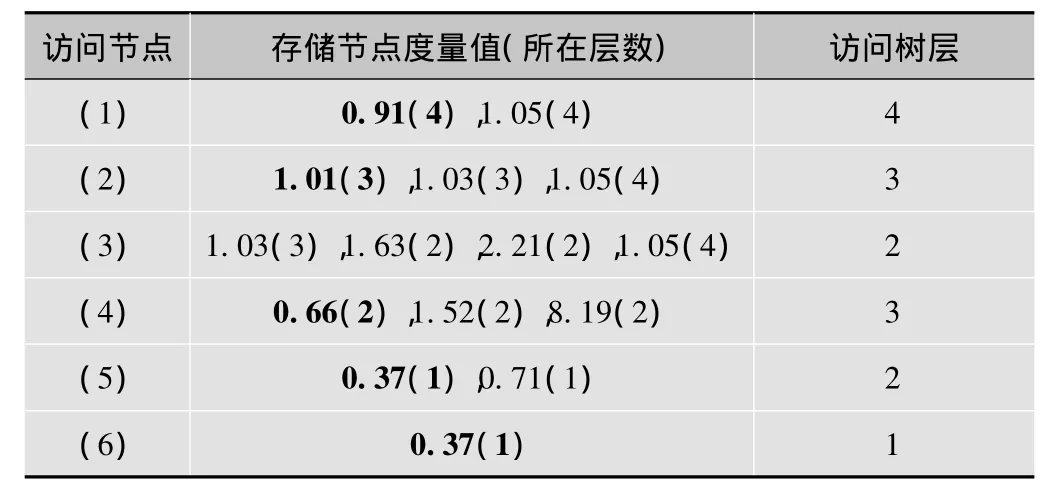
表2 MCTS搜索状态表

从表中可以看出，要达到准确输出，PSMCTS算法在搜索树层时，每层的存储空间中最多需保留3个分支节点，而MCTS最少需保留4个［9］，这使得PSMCTS算法在降低存储空间需求量方面存在着进一步优化的空间，并且这一优势会随着星座点数的增多逐渐扩大。表中也体现出了PSMCTS算法在搜索步骤简化上的优势，由于可以更加准确地表示出节点的度量值并将存储空间进行缩小，使得存储的节点数降低并加速了树搜索过程，使得该算法更加快速和有效。

3 复杂度与性能分析

为了验证PSMCTS算法的有效性，本文进行了BER性能仿真分析和复杂度分析。信道与噪声选择均服从N(0，1)的高斯分布。

3.1 复杂度分析

在MCTS算法中，为了保证该算法能够实现，M必须有个最小的取值界限。根据文献［9］中对M值最小值的取值证明，可相应地将多符号差分系统中的M值最小界限取为(N-1)(L-1)+1，L为星座点数。在本文研究的系统中，分析以分组长度N=4，QPSK调制L=4，存储空间M≥(N-1)(L-1)+1并取最小值。对于ML算法，访问点数为L0+…+LN-1=(LN-1)/(L-1)，MCTS算法以及本文中提出的PCMCTS算法的访问点数通过仿真访问次数来计算得出，仿真结果如图4所示。

图4对文中涉及的各类算法在分组长度为4的情况下进行了对比，横纵坐标分别为信噪比和运算点数。

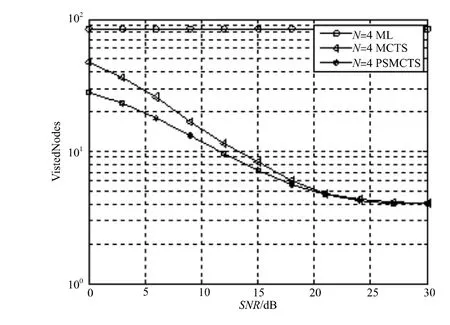
图4 复杂度分析对比图

结果表明，在分组长度和预设存储空间相同的情况下，针对同一种调制方式，PSMCTS在整体上均表现出对MCTS的优势，尤其是在低信噪比时优势更为明显，有利于系统平均复杂度的降低。

3.2 性能分析

对各种算法在测试环境下进行了性能仿真分析，仿真结果如图5。从图5可以看出，以性能最佳的ML最大似然算法为对比基础，本文提出的PSMCTS算法，由于有效地利用了概率排序算法的性能优势，在固定存储空间相同的情况下，其性能相比较MCTS有了一定提升，更加逼近ML算法。

图5 性能对比分析图

4 小结

本文基于MCTS算法，鉴于硬件存储空间约束以及在小存储空间的情况下，计算复杂度相对较大的问题，提出了改进型PSMCTS算法，该算法能够很好地利用DSPS算法与MCTS算法的优势，提供更好的性能表现。总体来说，PSMCTS算法既有较低的存储空间需求，便于硬件实现，又能在低信噪比区域降低计算复杂度，有利于降低系统的平均复杂度，同时能够逼近ML的检测性能，因此，它是一种较优的检测算法。

［1］WEIR Y.Differential encoding by a look-up table for quadrature-amplitudemodulation［J］.IEEE Trans.Communications，2013，59(1): 84-94.

［2］KIMJS，MOON SH，LEE I.A new reduced complexity ML detection scheme for MIMO systems［J］.IEEE Trans.Communications，2010，58 (4):1302-1310.

［3］SCHENKN，FISCHER R F R.A stopping radius for the sphere decoder:complexity reduction in multiple-symbol differential detection［C］//Proc.International ITG Conference on Source and Channel Coding(SCC).Siegen:［s.n.］，2010:1-6.

［4］ TAKAHASHI T，FUKUDA T，SUN C K.An appropriate radius for reduced-complexity sphere decoding［C］//Proc.International Conference on Communications，Circuits and System.Chengdu:［s.n.］，2010:41-44.

［5］应樱果，金小萍，金宁.多符号差分检测的低复杂度球形译码设计［J］.计算机工程与应用，2012，48(4):135-138.

［6］ MAO Xinyu，REN Shubo.Adjustable reduced metric-first tree search［C］//Proc.InternationalConferenceonWirelessCommunications，Networking and Mobile Computing(WiCOM).Wuhan:［s.n.］，2011:1-4.

［7］KIM T，PARK I.High-throughput and area efficient MIMO symbol detection based on modified Dijkstra’s search［J］.IEEE Trans.Circuits and Systems I:Regular Paper，2010，57(7):1756-1766.

［8］JASIKA N，ALISPAHIC N，ELMA A，et al.Dijkstra’s shortest path algorithm serial and parallel execution performance analysis［C］// Proc.the 35th International Convention MIPRO.Opatija:IEEE Press，2012:1811-1815.

［9］DAIYongmei，YAN Zhiyuan.Memory constrained tree search detection and new ordering schemes［J］.IEEE Journal of Selected Topics in Signal Processing，2009，3(6):1026-1037.

［10］CHANG R Y，CHUNGW H.Efficient tree-search MIMO detection with probabilistic node ordering［C］//Proc.IEEE International Conference on Communications.Kyoto:IEEE Press，2011:1-5.

［11］CHANG R Y，CHUNGW H.Best-first tree search with probabilistic node ordering for MIMO detection:generalization and performancecomplexity tradeoff［J］.IEEE Trans.Wireless Communications，2012，11(2):780-789.

［12］CUIT，TELLAMBURA C.Bound-intersection detection formultiplesymbol differential unitary space– time modulation［J］.IEEE Trans.Communications，2005，53(12):2114-2123.

Research of M emory Constrained Tree Search Based on Probabilistic Sorting

ZHU Ruixin，JIN Xiaoping，FENG Huizhen
(Department of Information and Engineering，China Jiliang University，Hangzhou 310018，China)

Considering the current MIMO system shortcomings of large storage space requirements and high complexity inmultiple-symbol differential detection algorithm，a probabilistic sortingmemory constrained tree search algorithm(PSMCTS)using performance advantage of sorting algorithm and storage advantage of MCTS is proposed.Through theoretical analysis and simulation，PSMCTScan effectively inherit the MCTSalgorithm good advantage，dynamically adapt to the preset storage space，and suitable for hardware implementation.Using sorting algorithms improved the detection performance，and the performance is close to ML algorithm under fixed memory requirement.The algorithm also solves the high computational complexity problem of MCTSalgorithm in small storage capacity conditions under the low SNR region.Therefore，PSMCTS is a good scheme in communication systems.

MIMO;probabilistic sorting;MCTS

TN911.23

A

�� 京

2014-05-16

【本文献信息】朱瑞鑫，金小萍，冯会真.基于概率排序的存储约束树形搜索算法的研究［J］.电视技术，2014，38(23).

国家自然科学基金项目(61071119);浙江省自然科学基金项目(Y1091155;LQ12F01010);东南大学国家移动通信研究实验室开放性研究基金项目(2011D18)

朱瑞鑫(1990—)，硕士生，主研通信系统、检测算法及软件;

金小萍(1978—)，硕士生导师，主研移动通信网络技术、编码与检测等;

冯会真(1973—)，讲师，主研通信电路、射频通信等。