并列建筑物周围风场的数值模拟

陈善群，田顺年，廖 斌，杨 明

（1.安徽工程大学 建筑工程学院，安徽 芜湖 241000；2.中国中铁四局重庆分公司，重庆 400010）

近些年来高层建筑得到了飞速发展，风荷载是高层建筑的主要控制荷载，风对高层建筑以及建筑物周围环境的影响巨大.在人们日益关心人居环境的今天，有必要对高层建筑物周围风场和风压进行全方面系统地研究，为评估建筑的城市规划及建筑设计的合理性提供重要的参考数据.

国内外学者对建筑周围风环境进行了大量数值模拟.R.Yoshie等人［1］使用k－ε模型、DSM、RANS以及LES等湍流数值模型对日本东京现实街区（新泻、新宿）建筑群风场模型进行数值模拟.B.Blocken和J.Carmeliet［2］使用CFD方法在不同风向、不同风速条件下，对不同类型的高层住宅建筑绕流风场进行数值模拟，找到了在高层住宅建筑户外使人感觉到舒服的风场条件.汤广发等［3］对一栋10m×10m×10m的建筑物采用k－ε湍流模型进行绕流计算，得到了建筑物表面压力分布及建筑周围速度矢量图.马剑等［4］采用基于Reynolds时均N－S方程和RNGk－ε湍流模型的数值研究方法，分别对具有风洞试验结果的单幢方形截面建筑和多幢矩形截面建筑组成的建筑群周围的风环境进行了数值模拟.虽然对建筑风环境的研究显示了蓬勃生机，但大多集中在对单个建筑物的研究，对多个建筑物建筑物绕流及其相互干扰问题的研究较少.建筑物群周围风绕流特性更加复杂，对数值模拟提出了更高的要求.

本文拟采用标准k－ε湍流模型对并列建筑群风场进行数值模拟，研究单体建筑物高度、并列建筑物高差及并列建筑物间距等因素对并列建筑周围风场变化的影响.

1 建筑物风场的数值模拟理论

1.1 控制方程

建筑物风场湍流流动的基本控制方程为Navier－Stokes方程组［5］，包括连续性方程和动量方程.在笛卡尔坐标系下，将连续性方程和动量方程以张量形式写出，分别为：

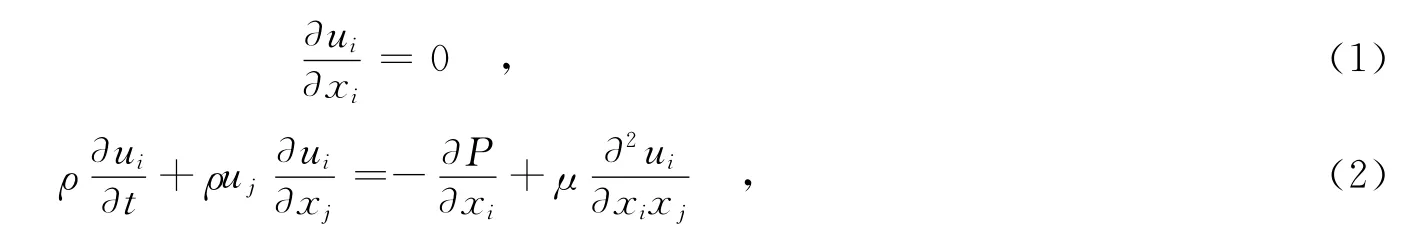
对连续性方程和动量方程分别进行时均化处理，得到基于雷诺平均的连续性方程和动量方程：

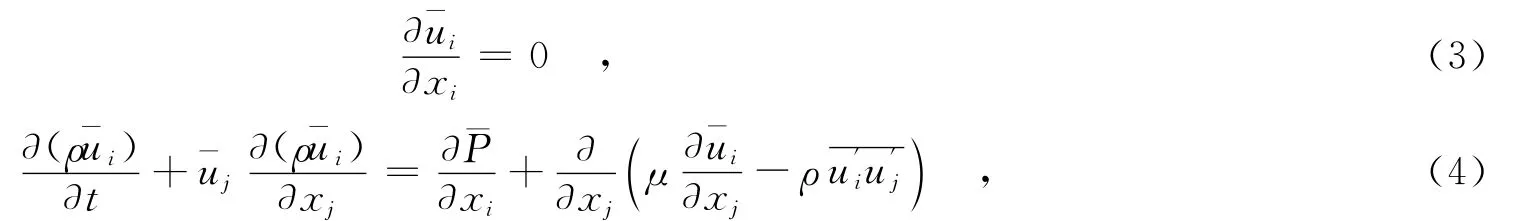
式中，xi为空间位置坐标为i方向的时均速度；¯P为时均压力；ρ为空气密度；μ为空气动力粘性系数，为雷诺应力.

1.2 标准k－ε模型

标准k－ε模型是建立在半经验公式模型的基础上，模型输运方程组源于湍流动能k和湍流耗散率ε.本文采用应用最广泛也最成熟的标准k－ε两方程模型.其中，湍流动能k方程：

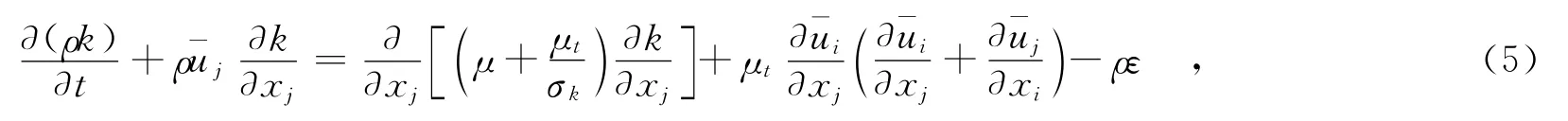
湍流耗散率ε方程：

由于本文所模拟的计算模型为定常工况条件下，可将动量方程（4）、湍流动能k方程（5）和湍流耗散率ε方程（6）简化为如下形式：

式中：μt为湍流动力粘度，表达式为为模型常数，取值为Cμ＝0.09，Cε1＝1.44，Cε2＝1.92，σk＝1.0，σε＝1.3.

2 方柱绕流模拟验证

2.1 计算模型的建立

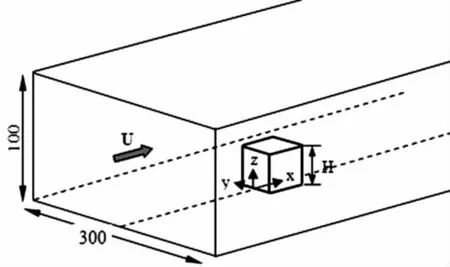
图1 方柱绕流计算域

方柱绕流计算域如图1所示，放置在通道中轴线上的立方体柱边长H为50mm，计算区域长1 250mm，宽为300mm，高为100mm.计算区域采用非均匀网格，靠近方柱区域网格布置较密集，计算域边界网格较稀疏的，最小网格间距小于2.5mm.通道高作为特征长度计算的雷诺数与Martinuzzi和Tropea的实验取值一致.

2.2 边界条件的设定

入口边界条件：速度入口条件，设定空气流的水平速度恒为1.6m/s，其他方向的速度梯度为零，压力在各个方向的梯度为零.出口边界条件：压力出口条件，即沿着出口方向的压力梯度为零.表面（壁面）边界条件：采用固壁无滑移边界条件，即速度在各个方向的梯度为零，压力的法向倒数也为零.

2.3 计算结果与分析

图2 X＝31.25mm，Y＝0处流向速度对比

图3 X＝50mm，Y＝0处流向速度对比

Y＝0处，X＝31.25mm、X＝50mm截面x方向速度与实验数据的对比结果如图2、图3所示.其中U/Ue表示计算速度与来流速度的比值；Z/H表示z方向坐标值与模型高度H的比值.由图3可知，本文数值计算结果与实验数据吻合良好，验证了建筑物风场的数值模拟理论在建筑物风场数值计算中具有相当的精确度和良好的适用性.

3 并列建筑物周围风场数值模拟与分析

3.1 并列建筑物计算模型的建立

对于并列建筑物共设置两单体建筑模型，如图4所示，其建筑底部截面为边长L为20m×20m的正方形.计算域长宽均为200m，高度取较高建筑高度的两倍，速度入口界面距并列建筑60m.两建筑高度分别为H1、H2，建筑物之间间距为D.

图4 并列建筑物风场计算域

为研究单体建筑高度、并列建筑高差及并列建筑间距等因素对并列建筑周围风场变化的影响.本文共建立了10种不同参数的并列建筑物风场模型，各种模型参数如表1所示.计算域网格的划分如图5所示.在三维模型壁面处附近用非结构性网格进行加密，较远处采用均匀网格，其网格间距最小尺寸取值在1～4m之间.并列建筑物模型其网格单元数在40万左右.

图5 并列建筑物风场计算域网格总体划分

表1 各种模型参数分项表

3.2 边界条件的设定

入口边界条件：速度入口条件，按照对应实际中6级强风（风速10.8～13.8m/s），本次风场模型中取11.0m/s，即设定空气流的水平速度恒为11.0m/s，其他方向的速度梯度为零.出口边界条件：压力出口条件，即沿着出口方向的压力梯度为零.表面（壁面）边界条件：采用固壁无滑移边界条件，即速度在各个方向的梯度为零，压力的法向倒数也为零.

3.3 计算结果与分析

（1）并列建筑物高度H1＝H2，两建筑物之间间距D相等.模型1、3、10间隔中心截面速度沿高程变化如图6所示.由图6中可知，3种模型速度变化曲线都可分为上升段和平缓段.上升段是近地面处，由于地面的阻滞作用，风速较小，随着高程上升，风速快速上升直到极值点，在后方平稳段，风速有缓慢下降并逐渐趋于稳定.在两建筑物之间间距D相等的条件下，随着建筑物高度的增加，间隔中心截面速度呈上升趋势且速度极值点高程同样呈上升趋势，但风速平稳段速度大小呈下降趋势.

（2）并列建筑物高度H1＝H2，两建筑物之间间距D不相等.模型3、6、7间隔中心截面速度沿高程变化如图7所示.由图7可知，在两建筑物高度H1＝H2且保持不变的条件下，随着两建筑物之间间距D的逐渐减小，速度变化曲线凹凸变化愈发明显，甚至可以清楚地发现，当并列建筑物间隔过小，不超过建筑高度的1/8时，风速大小甚至减小到0，即风无法正常通过两建筑物的间隔.

（3）并列建筑物高度H1≠H2，两建筑物之间间距D相等.模型2、3和模型8、9间隔中心截面速度沿高程变化如图8所示.由图8可知，在两建筑物之间间距D相等的条件下，并列建筑物高度H1≠H2时，模型2、3和模型8、9间隔中心截面速度变化趋势非常接近，说明并列建筑两建筑物高度差对间隔中心截面速度影响比较小.

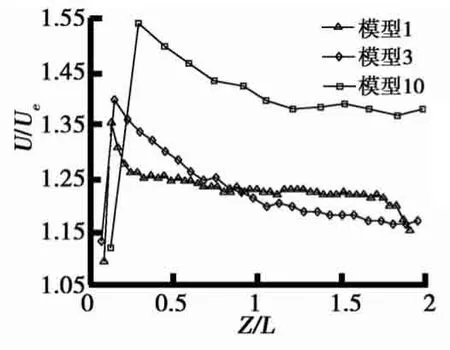
图6 模型1、3、10间隔中心截面速度沿高程变化

图7 模型3、6、7间隔中心截面速度沿高程变化

图8 模型2、3和模型8、9间隔中心截面速度沿高程变化

4 结论

以矩形柱模型简化代替实际建筑模型，建立了10组并列建筑群的计算域，采用标准k－ε湍流模型进行数值模拟，对数值模拟结果进行对比分析，得出单体建筑物高度与并列建筑物高差对于间隔处周围风场的影响是协调统一的.当单体建筑物越高，其对于间隔处风速的汇聚增幅作用越大，风速达到最大的高程越高.当相邻建筑物高差越大，其风速增幅会相对降低，同时最大风速处高程也相对下降；单体建筑物高度与并列建筑物间距对并列建筑物周围风场的共同影响.当间隔处间距过小时（D≤0.125H），风无法从间隔处正常通过.当单体建筑物高度适当（H≤40m）且不变时，间距大小与风速增幅成反比，且随着间距的缩小，风速变化曲线会呈现不同的变化趋势，但风速最终稳定在约为1.2倍的输入风速.当间隔间距D≥0.125H，且建筑物单体高度增加到一定高度时（H≥60m），风速变化曲线就不再稳定于1.2倍输入风速，而是随高程增加而不断减低，风速曲线成下降趋势，最终达到与输入风速.

［1］ RYoshie，A Mochida，Y Tominaga，et al.Cooperative project for CFD prediction of pedestrian wind environment in the Architectural Institute of japan［J］.Journal of wind Engineering and Industrial Aerodynamics，2007（95）：1 551－1 578.

［2］ B Blocken，J Carmeliet.Pedestrian wind conditions at outdoor platforms in a high－rise apartment building：generic subconfiguration validation，wind comfort assessment and uncertainty issues［J］.Wind and Structures，2008（11）：51－70.

［3］ 吕文瑚，汤广发，文继红.建筑数值风洞的基础研究［J］.湖南大学学报，1994，21（6）：114－118.

［4］ 马剑，程国标，毛亚郎.基于CFD技术的群体建筑风环境研究［J］.浙江工业大学学报，2007，35（3）：351－354.

［5］ 殷惠君，张其林，周志勇.标准低矮建筑 TTU 三维定常风场数值模拟研究［J］.工程力学，2007，24（2）：139－145.