巧用平均数求解物理问题

2014-07-01张荣登

教育教学论坛 2014年22期

关键词：荣登双江平均数

张荣登

（云南省临沧市双江自治县委党校，云南双江 677300）

巧用平均数求解物理问题

张荣登

（云南省临沧市双江自治县委党校，云南双江 677300）

要做好物理教学工作，必须关注数学知识的应用，恰当地挖掘学生的数学知识并指导学生在物理问题中的应用是物理教师的一种必备素质。结合高中物理与数学的实际，通过巧用平均数求解物理问题，来说明物理教学如何恰当的应用数学知识，为物理教学服务。

平均数；物理；数学；图象；知识迁移

物理教学中的概念教学、物理规律教学、实验数据处理都必须以数学作为工具，学生数学水平如何，可以说直接关系到物理教学的成败。物理教学中最重要的是物理概念和物理规律的教学，物理教学中，大多数概念和所有的物理规律必须用数学语言来描述。由于数学和物理有密切的关系，所以，指导学生准确而恰当地在物理中使用数学知识，是提高物理教学的方法之一，下面平均数在求解物理问题中的应用来说明：

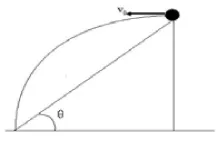
数学中，因为（a-b）2=a2-2ab+b2且（a-b）2≥0，所以a2+b2≥2ab。这样自然得到，如果a≥0，b≥0则当且仅当a=b时取等号，称为算术平均数，称为几何平均数，所以的含义是两个不小于“0”的数的算术平均数不小于（即大于或等于）这两个数的几何平均数。由于，所以当a+b为定值S（即a+b=S）时，，即两个不小于“0”的数的和为定值时这两个数的积有最大值且仅当a=b时有最大值。且积的最大值为abmax=[2]同样道理，当ab为定值S时，因为，即a+b≥即两个不小于“0”的数积为定值时，这两个数的和有最小值且仅当a=b时有最小值。最小值为以上的数学结论在物理中有重要意义，正确应用上述结论不但可使物理上的计算简便，而且对正确理解和应用数学知识解决具体问题有重要意义。通过用数学知识解决物理问题，对培养知识的迁移能力有重要意义。下面举几个具体的例子加以说明。例1：某金属带电荷10-8库，一与地隔缘的金属球，与之相接触，然后移开到相距1米的距离，问两金属球之间的库仑力最大为多少牛顿？解：已知r=1米，Q1+Q2=10-8库，求Fmax。根据库仑定律且Q1+Q2=10-8（定值），Q1≥0，Q2≥0，，代入k、r值，牛。答：两金属球之间的库仑力最大为牛顿.例2：如图所示，斜坡长为S，斜坡高与斜坡长的比为，在坡顶以V0的水平速度抛出一物体，刚好落在坡底，问物体在做平抛运动过程中与斜面的高度最大值是多少？解：设斜坡长为S，高为h，s′为出发点到斜坡底的水平距离，根据物体在做平抛运动时有所以