全自动装订机空间凸轮轮廓曲面方程

张书 殷勤

（中山职业技术学院电子信息工程系，广东中山 528404）

全自动装订机空间凸轮轮廓曲面方程

张书 殷勤

（中山职业技术学院电子信息工程系，广东中山 528404）

文章结合共轭曲面理论，利用空间回转变换张量法，对全自动装订机空间圆柱凸轮的机构几何学和运动学进行了全面分析，并以此为理论基础，推导出空间凸轮的轮廓曲面方程，通过将该方程与凸轮机构的啮合曲线方程进行联立，可以对空间圆柱凸轮轮廓曲面上各个点的坐标进行唯一确定，从而为提高空间凸轮的加工精度、改进其加工方法奠定坚实的理论基础。

轮廓曲面方程；空间凸轮；全自动装订机

0 前言

在当前的自动机械设计和制造中，常常会使用空间凸轮机构代替平面凸轮机构，充分体现出其自身体积小、刚性好、结构紧凑、传动扭矩大等优点[1]。而作为一种常用的办公设备，装订机在金融、图书及档案等部门得到了十分广泛的应用。将两者集合起来，实现全自动装订机的空间凸轮结构，可以对传动机构进行简化，提高装订的速度和可靠性，以及装订质量[2]。空间凸轮的轮廓方程是设计的重要内容，对设计、制造及检验空间凸轮至关重要。本文采用回转变换张量法[3]，推导全自动装订机空间圆柱凸轮机构凸轮廓面方程的计算公式。

1 结构原理

如图1所示，在全自动装订机凸轮机构中，从动件载体3与空间圆柱凸轮6是处于平行状态的。空间圆柱凸轮6会绕着载体轴线，作匀速旋转。从动件载体3上安装有从动滚子4，并依靠其运动，带动自身进行同步运动。而安装在从动件载体3上的下铆头2，可以通过向上的挤压作用，完成压铆的过程。

图1 空间圆柱凸轮机构示意图

2 建立曲面方程

要想建立圆柱凸轮机构的工作曲面方程，需要结合所有已知条件，针对两大要素进行计算，两个要素分别为滚子曲面方程和凸轮曲面的方程。凸轮机构自身的滚子曲面表现为圆柱体，形状较为简单，可以根据己知条件直接列出。而凸轮曲面则属于空间不可展曲面，形状和结构都相对更加复杂，难以利用已知条件直接得出。在这种情况下，需要使用简单的滚子曲面方程，结合相应的曲面啮合原理以及矢量回转变换，进行间接求解。

2.1 建立坐标系

在圆柱凸轮机构中，凸轮的运动主要是定轴转动，从动滚子则作曲线运动，为了方便研究，建立如图2所示的四个坐标系[4,5]。

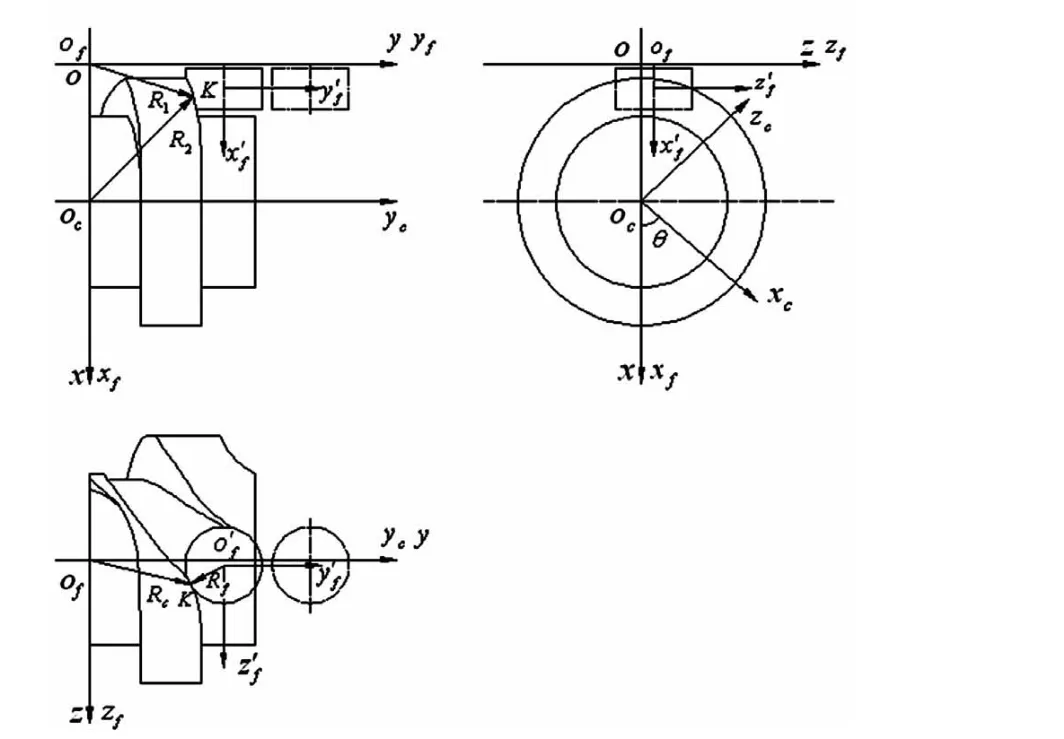
图2 空间圆柱凸轮机构运动变换关系图

2.1.1 固定坐标系o-xyz

y轴与从动件载体轴线保持重合，凸轮回转轴(yc)以及从动件载体的轴线的公垂线则与x轴保持重合，同时，在yc与y交叉显示的平面内，设x轴与y轴的交点为原点o，设x轴yc与的交点为oc，正向x轴由o指向oc，y与yc保持平行。

2.1.2 从动件坐标系of-xfyfzf

假设原点of与o处于重合状态，则当t=0时，与固定坐标系重合。从动件坐标系会随着从动件的运动，沿y轴进行直线移动，使用s表示其位移。

与从动件坐标系一样，滚子坐标系也是与从动件固结的坐标系。取滚子基准点为坐标系原点，保持坐标轴与从动件坐标系的相应坐标轴平行。除原点′f与of不重合外，滚子坐标系与从动件坐标系是基本一致的。该坐标系的引入，主要是为了对从动曲面的方程进行简化。

2.1.4 凸轮坐标系oc-xcyczc：

该坐标系是与凸轮固结的坐标系。其中，凸轮的回转轴为yc，始终与y平行，取凸轮曲面的基准点为原点oc。坐标系随着凸轮的运动，绕yc轴进行定轴转动，用θ2表示其位移角。

2.2 空间圆柱凸轮轮廓曲面方程

图3 空间圆柱凸轮机构的矢量关系图

图3为凸轮机构的矢量关系图，图中表示的是在t瞬时，滚子曲面与凸轮曲面在K点啮合时的情况，矢量代表从动件与凸轮之间存在的运动关系与几何关系。

图示中，c=ooc代表y与yc之间的距离，即凸轮机构的中心距；lh表示轴到yf轴之间的距离，也就是滚子的悬臂长度。

将相应的数值代入各有关量的坐标表达式，通过计算和变换，就可以得到凸轮轮廓曲面方程的坐标表达式：

3 啮合曲线方程

通过(1)可以看出，凸轮的曲面方程Rc是十分复杂的，不可能利用（1）式直接求出Ki，因此，需要首先求出点的几何位置参数βf(或δf)，又或者βf和δf的关系表达式，也就是接触线方程，然后根据两式的结合，求出Rc。在凸轮机构中，空间曲面的啮合方程[6]为：

其中，V12表示凸轮曲面与滚子曲面在接触点位置的相对滑动速度；n1表示接触点位置的单位法向矢量。

求解可得

(3)式就是空间圆柱凸轮机构的啮合曲线方程。通过将（1）与（3）进行联立，就可以对空间圆柱凸轮轮廓曲面上的各点坐标进行唯一的确定，结合凸轮曲面各点的坐标值，可以对完整的凸轮进行加工。

空间圆柱凸轮曲面坐标

4 结语

综上所述，结合相应的空间啮合原理，利用回转变换张量法，对全自动装订机凸轮轮廓的廓面方程进行了推导，优化了空间凸轮机构的运动学及动力学，极大地提高了空间凸轮的加工精度，并对其加工方法进行了改进，推动了相关制造行业的发展。

[1]赵镇宏，尹明富.空间凸轮廓面方程及压力角的精确解[J].山东工程学院学报，2000，14(3)：47～48.

[2]全自动装订机凸轮机构从动件运动规律[J].轻工机械，2009，27（3）：15～17.

[3]牧野洋(日本).自动机械机构学[M].北京：科学出版社，1980.

[4]赵雪松，高洪.空间圆柱凸轮轮廓曲面的计算机生成方法[J].机械传动，2008，32（3）：59～60.

[5]葛正浩，蔡小霞，王月华等.应用包络面理论建立弧面凸轮廓面方程[J].机械设计，2004，21（2）：28～29.

[6]王其超，牟敦华，陶学恒等.平而包络弧面分度凸轮机构凸轮廓面方程与啮合特性的研究[J].机械设计，1998，5：11～13.

A

1003-5168(2014)04-0196-02