考研成绩的路径分析及SAS程序

张学新

(湖北工程学院数学与统计学院，湖北孝感 432000)

考研成绩的路径分析及SAS程序

张学新

(湖北工程学院数学与统计学院，湖北孝感 432000)

本文阐述了结构方程模型与路径分析的原理，并基于某校2011-2013年理科考研情况的调查数据，利用路径分析方法研究考研英语、考研政治、专业课一、专业课二、学校类别、体育基础对理科考研成绩的作用路径及影响力度，给出了路径分析的SAS实现过程。

结构方程模型；路径分析；CALIS过程；理科考研成绩；效应分析

当面临多个因变量，或者一个变量既是自变量又是因变量时，多元回归显得不能兼顾，结构方程模型则显示出优势。结构方程模型(SEM)泛指一组实证现有理论有效性的统计模型，是单因素方差分析、多元回归分析等广义线性建模过程的扩展。它的主要优点是可以研究由多个指标测度的潜在结构间的关系，适用于经验数据与非经验数据、截面数据、纵向数据。SEM包括路径分析(PA)、因果模型、协方差结构分析，是经济和行为科学中重要的统计工具。本文应用路径分析探讨理科学生的课程学习与考研成绩之间的相互关系。

关于理科学生考研成功率的影响因素，国内已有一些研究成果。朱璟[1]认为,惟有准确、完整、系统地掌握高等数学基础知识,灵活运用解题方法,注重综合分析问题和解决实际问题能力的培养,才能在考研中取得良好的效果。王艳洁[2]认为加强对学生的教育和管理，采用数学分层次教学法和开设选修课对提高考研率有一定的积极作用。苏国荣, 戴中寅[3]基于粗糙集理论中的属性依赖度原理，分析高考成绩、高等数学课程成绩和高等数学培训成绩对考研高等数学成绩的影响大小。王小清，林荣华[4]利用考研心态调查问卷，对影响大学生考研心态的因素进行相关性分析。这些文献通过对考研现状的调查，探讨了影响理科学生考研成功率的一些因素，但存在以下不足之处：一是仅通过简单的描述性统计方法来分析考研成功率的影响因素，没有估计影响的大小，分析不够精确；二是仅仅研究了应变量和自变量之间的直接作用，而没有考虑变量之间的间接关系。李建宁[5]利用路径分析实证山西省1983-1993年份的大学入学率与人均GNP、全社会劳动生产率、人均教育经费支出等因素之间的相互关系, 但没有给出用SAS 软件程序。

本文介绍路径分析原理，并结合我校2011-2013年理科考研情况的调查数据，给出路径分析的SAS 软件程序实例。

1 基本理论

1.1 路径分析的基本思想及概念

SEM与PA广泛应用于社会科学领域，其基本特征见参考文献[6-7]。SEM对结构理论的多元分析采用实证方法检验其中多个变量之间规定的因果关系，目标是确任一个假设的模型与采集的反应它的数据是否一致。SEM由两个部分组成，即测量模型和结构模型。测量模型把可观测响应“指标”与潜变量，有时也与可观察的协变量联系起来。结构模型则指定潜变量之间的关系，把潜变量在可观测变量上进行回归。路径分析则是结构方程模型的特殊情形，它只有可观测变量而无潜变量，只有一个结构模型，而且每个变量只有一个指标。完整的SEM包含路径分析与因子分析，使用潜变量考虑测量误差。

在PA和SEM中的基本概念：显变量(测量变量)，可直接测量；潜变量，不可直接测量的变量；外生变量，有出自它但没有进入它的路径(弯箭头只简单的描述变量间的相关性，不是路径)；内生变量，具有至少一条指向它的路径。由于测量有误差，所有的内生变量都附加一个误差项，表示内生变量未被解释的部分。

SEM路径图中常用图标的含义：圆或椭圆表示潜变量或因子，正方形或长方形表示显变量或指标，单向箭头表示单向影响或效应，双向(弯)箭头表示相关，单向箭头指向因子表示残差项，单向箭头指向指标表示测量误差。

结构理论中的内生变量的因果模式是先验的，即在PA中必须确定：(1)哪些路径是重要的(直箭头)；(2)外生变量的方差是什么；(3)外生变量如何与另一个关联(弯箭头或协方差)；(4)内生变量的误差项(扰动项)是什么。

1.2 路径系数

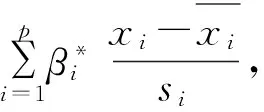
1.3 使用路径分析的步骤

(1)根据相关理论和文献资料，绘制一个没有路径系数的路径图。(2)以每一个内生变量为响应变量，以箭头指向它的变量为自变量建立线性回归方程。(3)改进模型。将路径系数不显著的路径从路径图中剔除，然后重新建立回归模型，给出各路径系数与残差。(4)模型评价：包括结构检验、相关性检验、测量模型可靠度检验、模型总体评价等。

2 实例影响考研成绩的路径分析

2.1 假设路径图

图1 考研成绩影响因素的初始路径图

本文数据来自湖北工程学院2011-2013届应用数学班和统计班考取研究生的所有学生。应用数学班的专业课一、专业课二分别指线性代数和高等代数，统计班的专业课一、专业课二分别指考研科目数学三和统计学。英语基础指考生的四学期的大学英语平均成绩，数学基础指三个学期的数学分析、概率论、常微分方程、高等代数平均成绩，四个学期的体育平均成绩称为体育基础，思想道德修养与法律基础、毛泽东思想邓小平理论、三个代表重要思想、马克思主义基本原理以及中国近代史纲要各科的平均成绩称为政治基础。对于考生的考研成绩取其考研成绩通知单上的分数。关于学校类别，对211学校或985学校赋值1，其它院校赋值0。初始路径图(ei表示残差项)设定为图1。

2.2 SAS统计分析过程

在SAS中引导作路径分析和SEM的程序是 CALIS过程[8]。 CALIS可用于分析协方差结构模型(实证因子分析)、含潜变量的线性结构方程、路径分析模型。它们中的变量间的假设关系依据方差和协方差指定，再拟合到一个可观测方差矩阵。CALIS过程的数据输入有三种方式：(1)含有每个变量的标准偏差和观测值数目的相关矩阵；(2)协方差矩阵；(3)使用原始数据作为输入。本文使用相关矩阵，数据一旦被输入，就得到用于实行路径分析的描述性统计和相关系数。

2.2.1 SAS程序

DATA path1(TYPE=CORR);

INPUT _TYPE_ $ _NAME_ $ V1-V10;

LABEL

V1 = '英语基础'

…

V10 = '考研成绩';

CARDS;

N . 55 55 55 55 55 55 55 55 55 55

STD . 4.1265 3.0780 9.0208 11.2919 12.0444 21.9459 23.6689 3.9220 0.4903 31.9286

CORR V1 1.0000 . . . . . . . . .

CORR V2 .3602 1.0000 . . . . . . . .

……

CORR V9 .0937 -.0752 .1196 .1100 .03597 .0319-.01192 -.0695 1.0000 .

CORR V10 .0318 .2242 .2613 .4985 .5311 .6923 .5869 .1226 .1992 1.0000

;

PROC CALIS COVARIANCE CORR RESIDUAL MODIFICATION ;

LINEQS

V4 = PV4V9 V9 + PV4V1 V1 + E2,

……

V10 = PV10V4 V4 + PV10V5 V5 + PV10V6 V6 + PV10V7 V7 + PV10V8 V8+ PV10V9 V9 + E1;

STD

E1 = VARE1,

…

E5 = VARE5,

V1 = VARV1,

...

V9 = VARV9;

COV

V1 V2 = CV1V2,

…

V8 V9 = CV8V9;

VAR V1 V2 V3 V4 V5 V6 V7 V8 V9 V10;

RUN;

有关语句说明n =55是观测值数目。在PROC CALIS语句选项中，首先，COVARIANCE告诉SAS要使用协方差矩阵进行分析。即使把相关矩阵作为数据输入，SAS 仍为 CALIS过程计算协方差矩阵。CORR选项指定想要的输出以包括赖以分析的相关矩阵或协方差矩阵。RESIDUAL选项，输出绝对残差和标准化残差。MODIFICATION选项告诉SAS打印修正指标(如拉格朗日乘数检验等)。

LINEQS，给SAS提供特定的线性方程组，它们指定了要估计路径。其中的第一个可以理解为：V4通过V4和V9之间的路径、V4和V1之间的路径、与V4相关联的误差的方差而受到因果影响。接下来是标准差线，它指定要估计的方差。最后，COV语句指定所有需要估计的协方差。变量线则简单地列出了在分析中使用的变量。

提交程序运行后，产生长达26页的输出。其中，第11页包括迭代历史，显示ABSGCONV收敛准则得到满足。第13页显示拟合指数，RMSEA(近似误差平方根)= 0.0527，接近0.05， Bentler & Bonett的标准化拟合指数NFI=0.8244，均表明较好的拟合。第15页显示标准化的残差矩阵和10大标准化残差，这些值接近零，意味着拟合较好。第17页以原始形式显示每个路径系数，以及t值和标准误差。第19页提供了如下标准化的路径系数和各内生变量的复相关系数的平方。

V4 = 0.1409*V1 + 0.0968*V9 + 0.9840 E2

PV4V1 PV4V9

……

V10 = 0.1294*V4 + 0.0395*V5 + 0.4925*V6 + 0.3011*V7

PV10V4 PV10V5 PV10V6 PV10V7

+ 0.1126*V8 + 0.2041*V9 + 0.7247 E1

PV10V8 PV10V9

最后一个的标签表达式：考研成绩=0.1294*考研英语+0.0395*考研政治+0.4925*专业课二+0.3011*专业课一+0.1126*体育基础+0.2041*学校类别+0.7247 E1，它的=0.4749。从第20页开始是修正指标的列表，一直继续到26页输出结束。

2.2.2 修改并完成路径图的绘制

在线性回归方程中考虑双箭头，从路径图中剔除路径系数不显著的路径，然后重新建立回归模型，给出各路径系数与残差。修改后的路径如图2，其中括号内的数值为决定系数，括号外的数值为路径系数。

图2 考研成绩及其影响因素路径图

直接效应=自变量与考研成绩的直接路径系数，间接效应=各路径系数的乘积，表示自变量通过其他变量间接的影响考研成绩的程度。由图2可知，专业课一除了对考研成绩有直接效应外，还通过专业课二对考研成绩产生间接影响。具体求解如下：

Effpart

V10<- V7 V6;

run;

提交后，可得专业课一对考研成绩的直接效应为0.266，专业课一通过专业课二对考研成绩的间接影响为0.69×0.421=0.29049，专业课一对考研成绩的总效应为0.266+0.29049=0.55649。

同理得到专业课二对考研成绩的总效应0.60853，学校类别对考研成绩的总效应为0.33562，考研英语对考研成绩的总效应为0.11042，考研政治对考研成绩的总效应为0.09132。至此完成具有标准化路径系数的路径图。

3 结果与讨论

3.1 初步结论

根据以上的分析结果，可以得出以下初步结论：

(1)考研英语、考研政治、专业课一、专业课二和学校类别与考研成绩呈显著的正相关，而体育基础、英语基础、数学基础、政治基础对考研成绩有一定的影响，但是不显著，这可解释为大学期间平时的考试只考察基本知识，考生只针对要考试的内容来复习，复习不全面，因而成绩都相差不是很大，即各考生的平时基础成绩相差不大，因此对考研成绩的影响不是很显著，影响考研成绩的是考生考研期间的态度与心态。

(2)专业课一与专业课二有强的相关关系，这可以解释为二者在学习过程中有很多相通的地方；学校类别通过专业课二间接影响考研成绩，这是因为专业课二是学校自主命题，考试难度自然也有所不同；考研政治通过影响考研英语来间接影响考研成绩，在于考研英语和考研政治的许多命题与解题的方式大致相同，都以分析为主，需要较强的推理能力；考研英语与学校类别有直接的因果关系，虽然是统考试卷，但是学校对英语的划线却有所不同，因此考研英语也会影响到学校类别。

(3)对考研成绩总效应的大小排序分别为：专业课二(0.60853)、专业课一(0.55649)、学校类别(0.33562)、考研英语(0.11042)和考研政治(0.09132)。

3.2 讨论

本文路径分析的部分结论不完全符合预期的假设，这或许与样本容量大小有关。SEM是大样本技术，样本量依赖于模型复杂度、采用的估计方法及观测变量的分布特征。为了增加样本容量，本文合并两个不同专业的考生数据，但对专业课进行了区分，数学基础变量的取值也是根据专业课对应的必修课程来计算，这对最终的结果仍会产生一定的影响。实例分析表明，路径分析的确是一种检验显变量和潜变量之间的假设关系的综合统计方法，是一种表示、评估和测试变量间主要线性关系构成的理论网络的方法论。PROC CALIS路径模型语言非常容易设定路径模型，EFFPART 陈述能够清楚地给出直接效应、间接效应及总效应。因而利用SAS中的PROC CALIS作路径分析是非常便捷的。

[1]朱璟,邓鹏.立足考研看高等数学的学习[J].高等数学研究,2006,9(3):59-64.

[2]王艳洁.学生考研数学的现状分析及对策探讨[J].中国林业教育,2009,27(2):11-13.

[3]苏国荣,戴中寅.基于属性依赖度的考研高等数学成绩影响因素分析[J].苏州大学学报:自然科学版,2012,28(3):89-94.

[4]王小清,林荣华.影响大学生考研心态的因素探析[J].沈阳教育学院学报,2009,11(4):19-21.

[5]李建宁.路径分析在教育发展战略研究中的应用[J].系统工程理论与实践,2001(8):142-144.

[6]Karada·,E.Basic features of structural equation modeling & Path analysis and its place and importance in educational research methodology[J].Bulgarian Journal of Science and Education Policy (BJSEP),2012,6(1):194-211.

[7]Lleras,Christy.Path Analysis.The Encyclopedia of Social Measurement[M].New York:Academic Press,2005.

[8]SAS Institute Inc. Chapter 25: The CALIS Procedure. SAS/STAT 9.2 User's Guide. Cary, NC: SAS Institute Inc,2008:828-1023.

Path Analysis of the National PG Entrance Exam Results and SAS Proc Calis

ZHANG Xue-xin

(School of Mathematics and Statistics, Hubei Engineering University, Xiaogan Hubei 432000,China)

This study expounds the detailed structural equation model and the principle of analysis, and based on the sample of a college science student’s grad-school entrance exam from 2011 to 2013, path analysis can be viewed as a special case to explore English exam, Politics exam , Specialized Course One and Two, the family of school and Physical basis by what paths and how much influences to affect post-graduate entrance exam scores. Finally, it gives example of path analysis using the SAS proc calis.

SEM; PA; proc calis; PG entrance exam score; effect analysis

2013-10-23

张学新(1966- )，男，湖北宜城人，湖北工程学院数学与统计学院讲师，博士，从事变点检测、可靠性统计分析研究。

O212.4

A

1008-178X(2014)01-0047-05