高灵敏度三维力矩传感器设计与标定

刘晓东， 顾小稳， 班 炯， 陈靖宇， 章晓明

(1.同济大学，上海 201804；2.上海航天控制技术研究所，上海 200233)

高灵敏度三维力矩传感器设计与标定

刘晓东1， 顾小稳1， 班 炯1， 陈靖宇1， 章晓明2

(1.同济大学，上海 201804；2.上海航天控制技术研究所，上海 200233)

为测量三维力矩并解决维间耦合问题，设计了一种测量微小力矩的电阻应变式传感器。分析了传感器电阻应变计组桥方案抑制维间力矩耦合的原理。通过有限元方法仿真计算出节点应变，实现传感器高灵敏度的目标。通过传感器静态标定实验得到了标定解耦矩阵，解决了由于加工误差和应变计粘贴误差带来的力矩耦合问题。实验表明：此传感器具有好的静态性能，线性度都控制在1 %之内，迟滞误差也控制在0.12 %以下。

三维力矩传感器；力矩耦合；高灵敏度；静态性能好

0 引 言

多分力/力矩传感器是一种新型的传感器，包括了多维位置传感器和多维力传感器等，针对笛卡尔坐标系中的3个力分量和3个力矩分量，多维力传感器的完整形式是六分力/力矩传感器[1]。近年来，多维力传感器广泛用在航天、航空、船舶、汽车、机械以及体育竞技等领域[2,3]。基于压电式只能测量到3个分力，不能测量力矩，所以,应变式多力传感器应用广泛。由于应变计贴在弹性体上，当弹性体受到某一方向上的力时，应变计都会产生大小不同的应变，于是各个分力之间就存在着耦合的现象。所以，在多力传感器设计上就存在着解耦的处理。

本文旨在对设计好的传感器进行有限元仿真，分析传感器主体结构和应变电桥分配的合理性，确保结构主体有足够的刚度和适宜的灵敏度。通过实验对传感器系统进行

静态标定，确定测试力矩与输出之间的关系，测试传感器静态性能，使用基于最小二乘法拟合的静态解耦算法对系统进行标定，确定标定解耦矩阵。

1 三维力矩传感器设计

1.1 传感器系统总体设计

根据系统框图(图1)，传感器测量到力矩后，通过动态应变放大器输出电压，再通过A/D转换卡的转换将电压数字数值传入PC进行数据的处理。

图1 传感器系统框图Fig 1 Block diagram of sensor system

1.2 传感器应变电桥设计

电阻式应变的测量电桥结构简单，具有灵敏度高、测量范围宽、线性度好、精度高和容易实现温度补偿等特点，是目前应用最广泛的一种测量电路。为提高灵敏度，电桥类型采用全桥，如图2所示[4]。

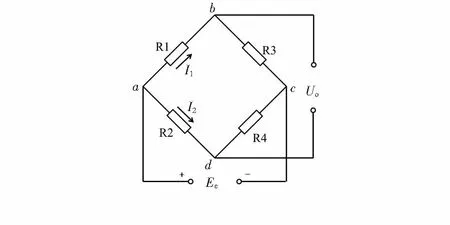
图2 电桥示意图Fig 2 Bridge sketch

1.3 应变计的组桥方案设计

如图3将圆柱分成三层，每一层贴4只应变计。第一层用于测量Mx，第二层测量My，第三层测量Mz。

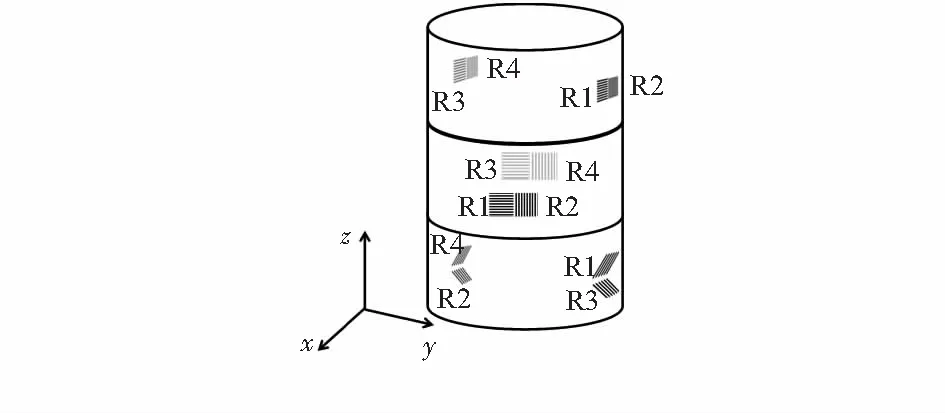
图3 结构示意图Fig 3 Structure diagram

如加载Mx，第一层的电阻应变计R1和R4的电阻变大，R2和R3的电阻变小，第一层电桥有电压输出。第二层电阻应变计R1和R3的阻值变化相同，R2和R4的阻值变化相同，第二层无电压输出。第三层电阻应变计R1和R3的变化相同，R2和R4的变化相同，第三层无电压输出，此时可测出Mx。

如果加载My时，第二层的电阻应变计R1和R4的电阻值变大，R2和R3的电阻值变小，第二层有电压输出。第一层的电阻应变计R1和R3的阻值变化相同，R2和R4的阻值变化相同，第一层电桥无电压输出。第三层的电阻应变计R1和R3的阻值变化相似，R2和R4的阻值变化相似，第三层电桥无电压输出，此时测出My。

如果加载Mz时，第三层的电阻应变计R1和R4电阻值变大，R2和R3的电阻值变小，此时第三层有电压输出。第一层的电阻应变计R1和R3的阻值变化相同，R2和R4的阻值变化相同，第一层无电压输出。第二层的电阻应变计R1和R3的阻值变化相同，R2和R4的阻值变化相同，第二层无电压输出，此时测出Mz。

定性分析后，可见该电桥能解决力矩耦合的问题。

2 传感器弹性元件的有限元仿真

图4所示为传感器力矩加载图，节点总共277 882个，六面体单元245 580个。在材料上，选取铝的弹性模量为72GPa，泊松比为0.33。

在力的加载上，为方便后续计算，加载Mx,My和Mz的大小均为1mN·m。在Patran中，力矩的加载方式是通过在上法兰盘的外径为100mm的外圆柱面施加2个位置相对、方向相反的大小为10mN的力，以此形成大小为1mN·m的力矩。

图4 力矩加载示意图Fig 4 Diagram of torque loading

分别进行两类有限元仿真：1)单独施加力矩Mx,My和Mz，2)同时施加Mx,My和Mz。在提取数据时，由于第一层和第二层的应变计都是水平或者垂直分布，在此方向的应变直接提取X，Y或者Z方向的应变值。而对于第三层上的45°方向的应变计，则应通过以下的公式获得

式中εn为任意方向的正应变，nx,ny,nz为该方向在总坐标系中的单位法向量的方向余弦，其他的是通过提取Nastran计算结果得到的每个节点的应变分量，应变如表1。

表1 不同力矩下电桥输出应变Tab 1 Bridge output strain under different torque

对表1中的结果进行分析，在有限元仿真中，当单独施加各个方向的力矩时，测试其他方向力矩的电桥没有电压输出，该传感器弹性体结构和应变电桥方案设计实现了原理上的无耦设计;且3个电桥的应变输出分别为0.49×10-6,0.46×10-6，0.63×10-6,(mN·m)-1。基于有限元的仿真结果和组桥方案及传感器弹性元件的设计，该传感器实现了高灵敏度的目标。

3 力矩测量平台的静态标定实验

3.1 标定解耦矩阵的推导

在实际机械加工制造中，弹性元件的制造和在应变计粘贴时仍存在误差，当传感器力矩输出时，3个力矩存在着细微的干扰，标定是解决这个问题的一个主要方法。解耦算法常用的是静态线性解耦算法，而在静态线性解耦算法中，有两种基本解耦方法：基于线性标定的静态解耦算法和基于最小二乘法拟合的静态解耦算法，现使用基于最小二乘线性拟合的静态解耦算法[5]。

传感器输入为广义外力分量Q，即Q=[Mx,My,Mz]T；系统输出为传感器的输出信号U，即U=[u1,u2,u3]T。根据最小二乘法的标定曲线拟合，可得到广义外力各分量分别单独加载时，力分量与各电桥输出电压之间的线性回归方程为

即uij=kijQi+bij;i=1,2,3;j=1,2,3.

(1)

每一个电桥输出电压是所有广义外力共同作用的结果，可表示为

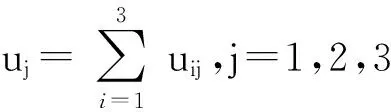
(2)

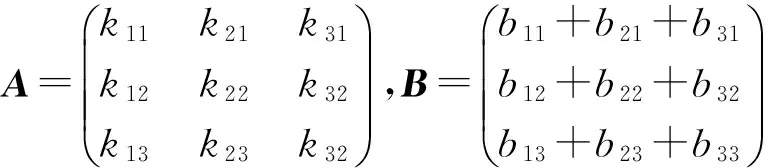
Q=A-1·(U-B).

(3)

3.2 静态标定实验

进行三维力矩传感器在3个方向上的力矩标定，标定所施加的单位力矩为7.84 mN·m，一直到78.4 mN·m。

3.2.1Mx方向的力矩标定

Mx的曲线图如图5所示。

进行最小二乘法拟合后得

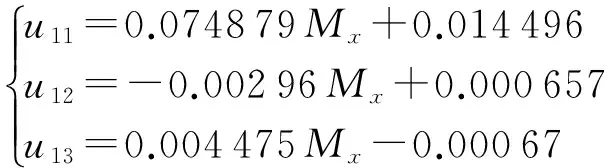
(4)

Mx电桥上灵敏度为0.075V/mN·m，线性度为0.662 578 %。

图6为回程误差图,回程误差为0.004 760 742V，迟滞为0.081 0 %。

图6 Mx 回程误差图Fig 6 Return error figure of Mx

3.2.2My方向的力矩标定

My曲线图如图7所示。

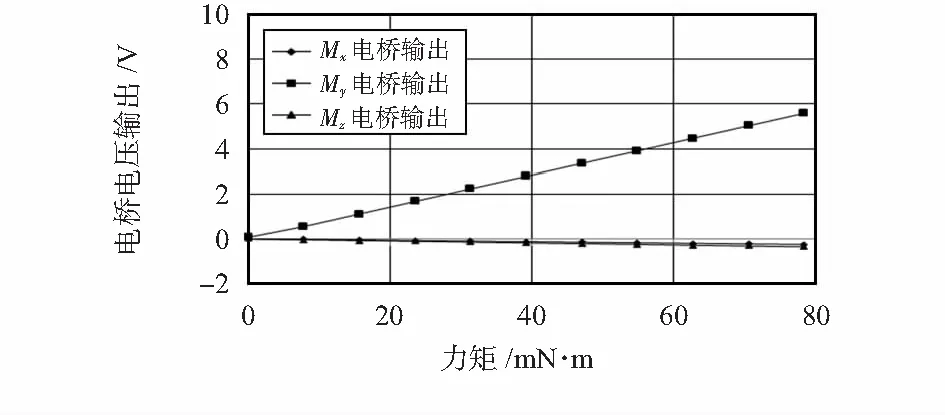
图7 My标定曲线图Fig 7 Calibration curve of My

进行最小二乘法拟合后得

(5)

My电桥上灵敏度为0.071V/mN·m,线性度为0.651 938 %。

图8为回程误差图,回程误差为0.000 683 594V，迟滞为0.012 3 %。

图8 My回程误差图Fig 8 Return error figure of My

3.2.3Mz方向的力矩标定

Mz曲线图如图9所示。

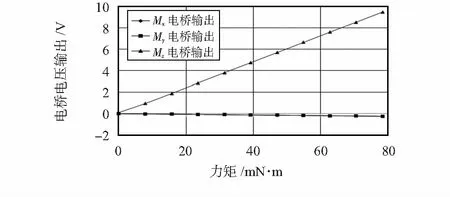
图9 Mz标定曲线图Fig 9 Calibration curve of Mz

进行最小二乘法拟合后得

(6)

Mz电桥上灵敏度为0.120 V/mN·m，线性度为0.796 6 %。

图10为回程误差图,回程误差为0.006 958 008 V，迟滞为0.110 3 %。

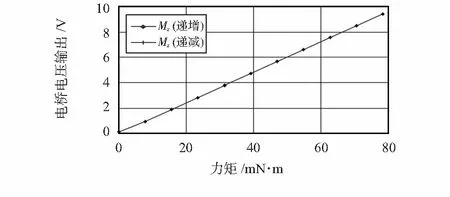
图10 Mz回程误差图Fig 10 Return error figure of Mz

3.3 标定实验总结

将各个参数投射到标定矩阵中对应的位置，得到标定解耦矩阵为

静态性能指标如表2所示。

表2 静态性能指标Tab 2 Static index performance

在3个电桥的静态性能中，线性度都控制在1 %之内，迟滞误差也控制在0.12 %以下，可见该传感器具备良好的静态性能。

4 结 论

1)设计了应变电桥方案，解决各相力矩耦合的问题。通过有限元仿真得出传感器主体在1 mN·m下产生的应变，即传感器的灵敏度。传感器主体设计满足设计标准，同时,应变计的组桥方案能够解决力矩的耦合问题。

2)完成了传感器的静态标定，得到标定解耦矩阵，解决了由于加工和粘贴应变计产生的力矩耦合问题，同时测试出传感器具备良好的静态性能。

[1] 张景柱.特种六分力传感器设计原理研究[D].南京：南京理工大学,2008.

[2] BL AutoTec.Multi-axis force/torque sensor [Z].BL AutoTec,2003:5-50.

[3] Ranjith Amarasinghe,Dzung Viet Dao,Toshiyuki Toriyama,et al.Development of miniaturized 6-axis accelerometer utilizing piezoresistive sensing elements[J].Sensors and Actuators,2007,134(2):310-320.

[4] 孟凡文．提高应变式传感器性能的几种方法[J]．中国仪器仪表,2003(4):34-37.

[5] 张景柱,郭 凯,徐 诚,等.六维力传感器静态解耦算法应用研究[J].传感器与微系统,2007,26(12):58-59,62.

Design and calibration of high sensitivity 3D torque sensor

LIU Xiao-dong1， GU Xiao-wen1， BAN Jiong1， CHEN Jing-yu1， ZHANG Xiao-ming2

(1.Tongji University，Shanghai 201804，China；2.Shanghai Aerospace Control Technology Research Institute,Shanfhai 200233,China)

To measure 3D torque and solve problem of coupling between two dimensional,a resistive strain sensor for small torque measuring is designed.The mechanism which curbs the dimension coupling is analyzed by the scheme of bridges of the sensor resistance strain gauge.Nodes strain is calculated by finite element method to achieve the goal of high sensitivity.Through static calibration experiment of sensor,calibration decoupling matrix is obtained and the problem of torque coupling due to processing error and strain gauge paste error is solved.Experimental results show that the sensor has good static performance,and linearity is controlled within 1 % and hysteresis error is below 0.12 %.

three-dimensional torque sensor； torque coupling； high sensitivity； good static performance

10.13873/J.1000—9787(2014)08—0076—04

2014—05—20

TP 202

A

1000—9787(2014)08—0076—04

刘晓东(1967-)，男，山西浑源人，工学博士，副教授,主要研究方向为精密测量与控制。