质量分布均匀球体的引力效应

柏 杨

（扬州大学附属中学 江苏 扬州 2250 02 ）

1 问题的提出

高中物理“万有引力定律”一节中，通过对牛顿研究的介绍，向学生呈现了万有引力定律的内容，并特别指出，公式中r为两个质点之间的距离，对于质量分布均匀的球体，r为两个球体球心之间的距离．为什么处理一个均质球对球外质点的吸引作用时，可以将球的质量集中在它的球心来处理呢？

2 问题的证明

设一密度均匀的球壳，它的厚度t比其半径r小得多，如图1所示．那么，对球壳外一个质量为m的质点P的引力是多少？

假设球壳上每一很小部分对质点P的作用力为Fi，根据万有引力定律，该力的大小应与球壳每一小部分的质量成正比，而与它和质点P之间距离的平方成反比，方向沿着它们之间的连线．然后，求得球壳上所有部分对质点P的合力，即为该均质球对质点P的作用力．

图1

设在A点处球壳的一小部分对质点P的引力为F1，而在球壳上离质点P同样远但位于和A点对称的B点处同样质量的一小部分对质点P的引力为F2，这两个力的合力为F1＋F2．由对称性可知，这两个力垂直O P方向的分量彼此抵消，而水平分量F1cosα与F2cosα相等．通过把球分为像这样一对一对的小块，可以看出，所有作用在质点P上力的垂直O P方向的分量都成对相互抵消了，则球壳对质点P的合引力只需考虑水平分量即可．

在球壳上取dS的一条圆带形状的质量元．此圆带长为2 π（rsinθ），宽为rdθ，厚为t．那么其体积为

dV ＝2 πt r2sinθdθ

设球壳密度为ρ，则圆带的质量为

d M ＝ρdV ＝2 πtρr2sinθdθ

即M ＝4 πtρr2

圆带对质点P所施的力是水平的，其值为

由图1可以看出

根据余弦定理

故有

将式（3）微分，得

2xdx＝2R rsinθdθ

即

将式（4）代入式（2），再将式（2）与式（5）代入式（1），从而消去θ与α，得

这就是圆带dS作用于质点P上的引力．

考虑球壳上每一质量元，即将式（6）对整个球壳所有圆带求和．这种求和是对变量x求出遍及整个球壳的积分．因为x的范围是从最小值R－r到最大值R＋r，所以

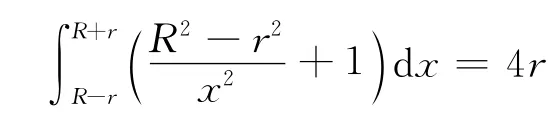
故合力为

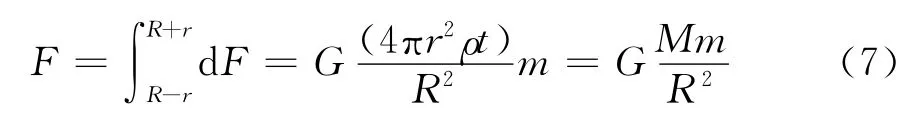
式中M为球壳的总质量．这个结果和假设质量为M与m的两个质点相距R时所求得的引力结果完全相同．即一密度均匀的球壳对球壳外一质点的引力犹如它的所有质量都集中于其球心时的引力．

一个实心球体可当作由大量同心球壳所构成．如果各层球壳具有不同密度，但每一球壳都具有均匀密度，则同样的结论也适用于这种实心球体．因此，对于像地球、月球或太阳在一定程度上也可视为这类球体的物体来说，讨论它们吸引外部物体时，就可以把它们当作质点来处理．

应该指出，上述的证明只适用于球体，且只适用于整个球体的密度不变或密度仅为半径的函数的情况．

3 问题的推论

推论1：均质球壳对内部一质点的引力为零．

证明：如图2所示，因为质量为m的质点位于球壳内部，所以R小于r，积分限是从r－R到r＋R．

图2

因为

所以 F＝0

这个结果，虽然不是显而易见的，却是合理的．因为球壳上处于对称位置的质量元对质点所施的力具有相反的方向，而总的抵消作用则决定于这一事实，即力正好与质点间的距离的平方成反比．据查，牛顿当年的证明如下．

图3

如图3所示，设一质点位于球壳内任意一点P处．假设球壳厚度与密度都是均匀的．以P为顶点作两个对顶小圆锥，在球壳面上所截的面积为dA1，dA2．设球壳的质量面密度为σ，则截面dA1对P点处质点的作用力为

式中的dΩ1为以P为顶点，向上开口的小圆锥的立体角．

同理，截面dA2对质点的作用力为

f2＝G m σdΩ2

式中dΩ2为以P为顶点，向下开口的小圆锥的立体角．而dΩ1＝dΩ2，所以f1＝f2，两截面对质点的合力为

f＝f1－f2＝0

通过壳内任意一点P作一平面把整个球壳分成两部分，以P为顶点可以作许多对对顶的小圆锥（每对小圆锥处于平面的两边），而把两半球壳表面分割．根据上述结果，每对对顶的小圆锥对P点处的质点的合引力为零，而平面两侧的球壳表面正好被这种对顶的小圆锥所分割，所以，整个球壳对壳内任意一点P处的质点的合引力为零．

推论2：如地球具有均匀密度，则在地球表面处g值为最大，而离开地球表面后，不论是向外还是向内，g值都逐渐减小．

证明：假设地球具有均匀密度，则当一质点进入地球内部越深时，地球对它所施的引力就变得越弱，因为在质点所在位置以外的球壳所含的物质对该质点没有作用力．当质点处在地球中心时，引力就变为零．因此，如地球具有均匀密度，则在地球表面处g值为最大，而离开地球表面后，不论是向外还是向内，g值都逐渐减小．

4 问题的应用

【应用1】如图4所示，若能沿着地球直径挖通一条穿过地球的隧道．

（1）证明落入隧道的一个质点的运动是简谐运动．（这里忽略所有摩擦力并假设地球具有均匀密度）

（2）若通过这个隧道来传递邮件，那么，从一端投入而从另一端递出需要多长时间？

（3）若使邮件沿着地球的某一直径的隧道传递，试求邮件通过地心时的速率有多大？

图4

解析：（1）离地球球心距离为r的一质点所受地球引力完全来自该质点位置以内的球体中的物质，外层球壳对该质点没有作用力．设地球密度是均匀的，其值为ρ，则在考虑引力作用时，半径为r的球体内的质量可看作集中于地球球心，设为M′，则M′＝．因此，作用在质点上的力为

式中负号表示引力指向地球球心．将M′的表示式代入上式，得

（2）此简谐运动的周期是

取ρ＝5．51 ×103k g／m3

G＝6．67 ×10－11N·m2／k g2

代入数据得

T ＝84 ．2m i n

传递时间为周期的一半，即约42 min．有意思的是，这个结论与以第一宇宙速度运动的结果一样．

（3）质量为m的邮件在距离地心为r处所受到的万有引力为

式中的负号表示F与r方向相反，根据牛顿第二定律得

即

其中

上面方程的解为

r＝Rcos（ω t＋φ）

可见，地心为其平衡位置，做谐振动的物体通过平衡位置时速率达到最大值，即

代入数据得

v＝7．9×103m／s

这个速度恰好是第一宇宙速度．

以上两个恰好并非偶然，其实是物体以第一宇宙速度做匀速圆周运动在x轴上的投影．

【应用2】如图5所示，如穿过地球的隧道不是沿着直径而是沿着一弦线．

（1）那么在这隧道内，物体的运动仍是简谐运动．这里假设地球密度是均匀的．

（2）试求周期．

（3）试问物体沿着这隧道运动的最大速率能否达到沿着直径隧道运动的最大速率？

图5

解析：（1）根据上例中所说的理由，质量为m的物体在隧道内距离地心为r处所受到的万有引力的大小为

其中ρ为地球的平均密度．

F在y轴上的分量为

其中ω2＝πGρ，此式为简谐运动的微分方程，因此，物体在隧道内的运动是简谐运动，且其圆频率与物体在沿着直径隧道运动时相同．

代入数据得

T＝84 min

（3）物体沿隧道做简谐运动的运动方程为

y＝y0cos（ω t＋φ）

式中y0为y的最大值，即隧道长度的一半．物体的运动速率为

物体的最大速率为y0ω，而物体沿着直径隧道运动的最大速率为R ω，显然y0ω＜R ω．所以，最大速率达不到沿着直径隧道运动时的最大速率．

其实地球内部g值随深度而改变的情况是，在地核内（离地面2900 k m以下）g的数值由10 ．37 m／s2单调地（非线性地）减小到零；离地面4000 k m以下，g的实际变化是不确知的．在地球内部、地核外各处的g值变化不大，这说明，地核外的平均密度比地核的平均密度小．实际情况是从地面到深度为33 k m处为地壳，平均密度为3．0g／c m3；深度从33 k m到2900 k m的范围为地幔，平均密度为4．5 g／c m3．

1 （美）R·瑞斯尼克，D·哈里德 ．物理学（第一卷第二册）．郑永，等译．北京：科学出版社，1985

2 彭大斌主编．物理竞赛教程（第四版）．上海：华东师范大学出版社，2012