局部残余变形对轴压钢构件承载能力的影响

何 飞 蒋首超 文 见

(同济大学建筑工程系，上海200092)

1 引言

钢结构杆件主要用于桁架结构和网架结构，或作为其他结构的支撑。钢杆件的受力特点是主要承担轴力，承担的弯矩可忽略不计。钢构件在使用过程中由于受到意外(如撞击)或灾害(如地震、火灾)作用，会产生不同程度的损坏，需要修复或加固。不论是试验研究[1]还是工程实践[2]，修复加固的重要依据和前提条件都是对受损构件承载能力的评定。国内外关于钢结构的检测、鉴定、承载能力评定、修复加固方法已有一定的研究，美国和日本是开展钢结构建筑检测鉴定和评估方法研究较早的国家，已经形成系统的抗震鉴定方法和评定标准。其中详细阐述损伤对构件影响的资料主要是FEMA352——焊接钢框架建筑的震后评估和修复建议准则[3]。FEMA352对钢结构受损根据不同部位(梁、柱、焊缝等)、不同类型(失稳、屈服、热影响区开裂、非热影响区开裂、横向扭屈等)进行划分，对每一种受损组合进行定性描述并给出损伤系数值，用以评定该种损伤，但是并没有给出定量的判断标准。

受损构件的承载能力是否降低、降低的程度有多大，对于这些问题国内外的定量研究较少。本文将对有局部残余变形的直缝焊接钢管和热轧等边角钢钢杆件的轴压承载力与局部残余变形量进行定量分析。钢管的局部残余变形为杆件中部凹陷，角钢的局部残余变形为杆件中部凸起，构件示意图如图1所示。

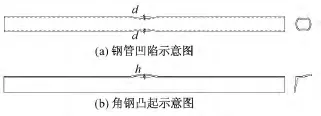
图1 有局部残余变形的钢杆件示意图Fig.1 Steel member with local residual deformation

2 钢管轴压承载力分析

钢管截面双轴对称，定量分析局部残余变形对轴压承载力的影响，采用规范公式、数值分析、试验验证三种方法。钢管截面为Φ83×6，面积A=14.51 cm2，回转半径 i=2.73 cm，长度 l=1.66 m，两端铰接;材料性质由材性试验得到:屈服强度 fy=466.31 N/mm2，弹性模量 E=2.06 ×105N/mm2。

2.1 规范公式求解

2.1.1 无局部残余变形的轴压承载力

根据《钢结构设计规范》(GB 50017—2003)[4]5.1.2 条，轴压承载力为

式中，φ为轴心受压构件的稳定系数;f为钢材的强度设计值。

由式(1)可得到Nmax=399.82 kN。

2.1.2 有局部残余变形的轴压承载力

在海洋平台受损构件的研究中，对凹陷的钢管求解轴向承载力时采用截面面积折算公式[5]:的计算如图2(a)所示。本文研究的凹陷截面如图2(b)所示，则面积折算公式为

图2 θ的表示Fig.2 Diagram of θ

根据《API RP 2A-WSD》[6]3.2.2.a 条，该类构件的允许抗压强度为

式中，E为弹性模量;K为有效长度系数;l为无支撑长度;i为回转半径。

得到fa=195.82 N/mm2;代入轴压承载力公式:

得到不同凹陷深度下的轴压承载力，计算结果如图3所示。

图3 不同凹陷深度的钢管轴压承载力Fig.3 Axial load-bearing capacity of different steel pipe

2.2 数值分析求解

本文采用通用有限元软件ANSYS进行数值分析。

2.2.1 模型描述

钢管模型如图3所示，采用有大变形功能的壳单元shell181进行建模。钢材采用理想弹塑性模型，弹性模量E=2.06×105N/mm2，屈服强度fy=466.31 N/mm2，泊松比 po=0.3，如图4 所示。

为了模拟两端铰接的支座类型，在钢管两端建立端板，约束端板X、Z两个方向的位移，在钢管截面的形心，即端板的圆心处施加Y方向的位移约束。选中模型l/2处对称的两个节点，施加位移约束来模拟钢管的凹陷，位移约束值不同代表凹陷深度不同。求解得到带凹陷这种局部残余变形的钢管，如图5所示。

图4 无凹陷钢管模型Fig.4 Model of steel pipe

图5 有凹陷钢管模型Fig.5 Model of dented pipe

2.2.2 轴压承载力计算结果

无凹陷钢管在轴向压力的作用下，杆件中部产生侧向位移;在加载的过程中，侧向位移不断增大，杆件中部开始进入塑性阶段，逐渐形成塑性铰;达到极限压力后卸载，侧向位移继续增大，杆件中部大面积进入塑性阶段，破坏时的Mises应力分布如图6所示。有凹陷钢管的破坏模式与无凹陷钢管相同;由于有凹陷，破坏时杆件中部的应力分布较不均匀，Mises应力分布如图7所示。ANSYS计算得到的不同凹陷深度钢管轴压承载力如图3所示。

图6 无凹陷钢管破坏时的应力Fig.6 Stress in steel pipe at failure

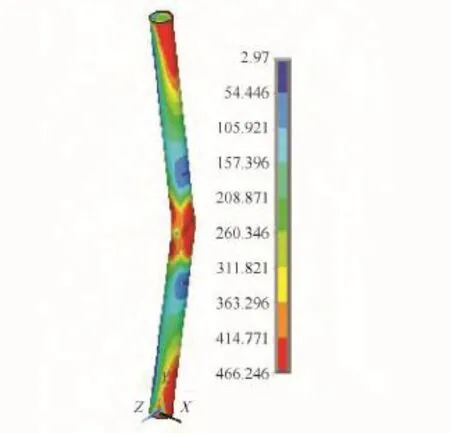
图7 有凹陷钢管破坏时的应力Fig.7 Stress at failure of dented pipe

2.3 试验验证

2.3.1 试验简介

钢管试件长1.50 m，采用可拆卸的双刀口支座来模拟两端铰接的情况，实际计算长度为1.66 m。通过液压千斤顶挤压试件产生局部凹陷。试件共2个，一个是无凹陷的钢管，一个是有局部凹陷的钢管，凹陷深度d=6.0 mm。采用反力架、千斤顶进行轴压加载试验，并测量试件的侧向位移、轴向位移、应变，得到无局部残余变形试件的极限承载力为353 kN，有局部残余变形试件的极限承载力为347 kN。2.3.2 试验结果

两种钢管的破坏模式与ANSYS分析结果相同，如图8、9。测得的轴压承载力如图3所示。

图8 无凹陷钢管试验Fig.8 Test of steel pipe

图9 有凹陷钢管试验Fig.9 Test of dented pipe

由图3可知，凹陷这种局部残余变形会降低钢管的轴压承载能力，且轴压承载力随凹陷深度的增大而下降;与试验、ANSYS分析结果对比，按照API规范公式计算得到的有凹陷钢管承载力明显偏低。

2.4 其他局部残余变形形式

采用ANSYS计算单边凹陷钢管的轴压承载力，计算结果与2.2节基本相同。单边凹陷会降低钢管的轴压承载力，承载力随凹陷深度的增大而下降，且下降速度比对称的凹陷形式快。

3 角钢轴压承载力分析

角钢截面单轴对称，定量分析局部残余变形对轴压承载力的影响，采用规范公式、数值分析、试验验证三种方法。角钢截面为∟70×6，宽厚比 b/t=12，面积 A=8.16 cm2，回转半径 i=1.38 cm，长度 l=1.66 m，两端铰接;材料性质由材性试验得到屈服强度fy=316.83 N/mm2，弹性模量 E=2.06 ×105N/mm2。

3.1 规范公式求解

目前没有定量计算带局部残余变形的角钢承载力公式，因此只有根据式(1)计算无局部残余变形角钢的轴压承载力，得到Nmax=81.32 kN。

3.2 数值分析求解

本文采用通用有限元软件ANSYS进行数值分析。

3.2.1 模型描述

角钢模型如图10所示，采用有大变形功能的壳单元shell181进行建模。钢材采用理想弹塑性模型，弹性模量E=2.06×105N/mm2，屈服强度fy=316.83 N/mm2，泊松比 po=0.3。

图10 无凸起角钢模型Fig.10 Model of steel angle

为了模拟两端铰接的支座类型，在角钢两端建立端板，约束端板X、Z两个方向的位移，在角钢截面的形心处施加Y方向的位移约束。选中模型l/2处两侧翼缘最外端的两个节点，施加位移约束来模拟角钢的凸起，位移约束值不同代表凸起高度不同。求解得到带凸起这种局部残余变形的角钢，如图11所示。

图11 有凸起角钢模型Fig.11 Model with protrusion

3.2.2 轴压承载力计算结果

无凸起角钢在轴向压力的作用下，杆件中部产生侧向位移;在加载的过程中，侧向位移不断增大，杆件中部开始进入塑性阶段，逐渐形成塑性铰;达到极限压力后卸载，侧向位移继续增大，杆件中部大面积进入塑性阶段，破坏时的Mises应力分布如图12所示。当凸起高度较小时，角钢的破坏模式与无凸起角钢相同，Mises应力分布如图12所示。随着凸起高度增大，角钢的破坏模式发生改变:杆件中部形成塑性铰，但侧向位移的方向改变。Mises应力分布如图13所示。ANSYS计算得到的不同凸起高度角钢轴压承载力如图14所示。

3.3 试验验证

3.3.1 试验简介

角钢试件长1.50 m，采用可拆卸的双刀口支座来模拟两端铰接的情况，实际计算长度为

图12 无凸起、凸起小的角钢破坏时的应力Fig.12 Stress in steel angle at failure

图13 有较大凸起角钢破坏时的应力Fig.13 Stress at failure with protrusion

1.66 m。通过液压千斤顶挤压试件产生局部凸起。试件共2个，一个是无凸起的角钢，一个是有局部凸起的角钢，凸起高度h=6.8 mm。采用反力架、千斤顶进行轴压加载试验，并测量试件的侧向位移、轴向位移、应变，得到无局部残余变形试件的极限承载力为70 kN，有局部残余变形试件的极限承载力为73 kN。

3.3.2 试验结果

试验试件的凸起高度较小，两种角钢的破坏模式相同且符合ANSYS的分析结果，如图15、图16所示。测得的轴压承载力如图14所示。

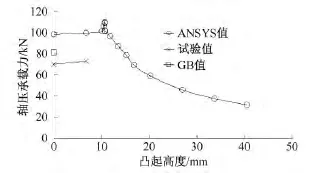
图14 不同凸起高度的角钢轴压承载力Fig.14 Axial load-bearing capacity of different steel angle

图15 无凸起角钢试验Fig.15 Test of angle steel

由图14可知，当凸起高度h＜10.7 mm时，角钢的轴压承载力会随着h的增大而增大，与试验现象吻合;h＞10.7 mm后，角钢的承载力随h的增大而减小。随着凸起高度的增大，角钢的破坏模式改变、轴压承载力产生了极值。产生这种现象的原因可能是凸起部分的屈服后强度、变形后杆件刚度的变化。有凸起这种局部残余变形的角钢轴压承载力不一定下降，需要根据具体的变形情况进行分析。

3.4 凸起高度对角钢轴压承载力的影响

采用ANSYS计算不同长细比、不同宽厚比的角钢在局部残余变形影响下的轴压承载力。由计算结果可知，在一定凸起高度范围内，角钢的轴压承载力并未下降，超过此范围后承载力随凸起高度的增加而下降，变化趋势与3.2节中ANSYS的分析结果相同。

图16 有较小凸起角钢试验Fig.16 Test with protrusion

根据《民用建筑可靠性鉴定标准》(GB 50292—1999)[7]，单个构件的安全性鉴定分为 au(不必采取措施)、bu(可不采取措施)、cu(应采取措施)、du(必须及时或立即采取措施)四个等级。钢结构主要构件的安全性按承载能力评定时，R/γ0S≥0.95为bu级。记没有局部残余变形的角钢轴压承载力为R，有凸起的承载力为Rh。以Rh/R≥0.95时凸起高度的最大值hmax为临界高度，得到临界高厚比hmax/t随长细比λ、宽厚比b/t的变化情况如图17所示。

由图17可知，长细比较大时临界高厚比随长细比的增加而增大，长细比较小时临界高厚比趋于水平，不同宽厚比的临界高厚比开始增大的转折点不同。角钢的长细比λ越大，其轴压承载力受λ的影响越大，局部残余变形对承载力的影响越小，因此临界高度hmax会随着长细比的增加而增大。

3.5 其他局部残余变形形式

采用ANSYS计算单边凸起、两边凹陷、单边凹陷、一边凸起一边凹陷的角钢轴压承载力，与3.2中两边凸起的计算结果进行对比。一边凸起一边凹陷的角钢破坏时杆件中部的侧向位移与凸起方向相同，破坏模式不发生改变，与两边凸起角钢不同。单边凸起、两边凹陷、单边凹陷的角钢，轴压承载力在一定凸起高度h(凹陷深度－h)范围内并未下降，超过此范围才下降，并且在这一过程中发生了破坏模式的改变，改变方式与两边凸起的角钢相同。

计算得到单边凸起、两边凹陷、单边凹陷角钢的临界高厚比，其变化规律与两边凸起的角钢相似，且基本大于两边凸起的值。图18给出了角钢∟70×6在不同局部残余变形形式下临界高厚比随长细比的变化情况。

图18 ∟70×6在不同局部残余变形形式下临界高厚比的变化Fig.18 Relation between slenderness ratio and critical height-thickness ratio of∟70×6 with different local residual deformation

3.6 不同的材料屈服强度

采用 ANSYS计算Q235、Q345、Q390、Q420 的角钢在有两边凸起这种局部残余变形情况下的轴压承载力，得到不同宽厚比的临界高厚比随长细比的变化情况，如图19所示。不同材料强度的临界高厚比变化规律相似，随着长细比的增加整体呈上升趋势。

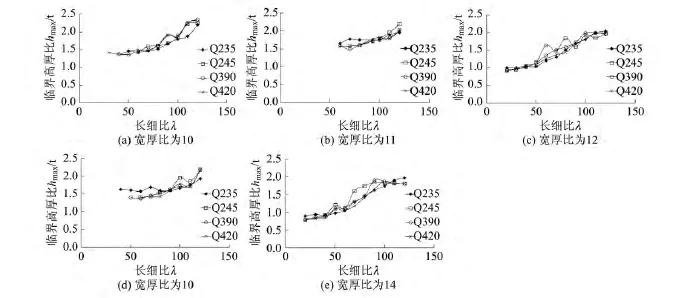
图19 不同材料临界高厚比的变化Fig.19 Relation between critical height-thickness ratio and material strength

4 结语

本文对有局部残余变形的钢杆件，采用规范公式、数值分析、试验验证三种方法分析了轴压承载能力的变化，对三种方法的结果进行对比，得出以下结论:

(1)有凹陷的钢管轴压承载能力随凹陷深度的增大而下降，按照规范APIRP2A计算出的承载力是保守的，使用它进行设计是偏于安全的。

(2)角钢翼缘凸起高度不同会改变破坏模式、影响轴压承载力，当凸起高度在一定范围内时，角钢的轴压承载力不会下降，超过此范围后承载力才会随凸起高度的增加而下降。

(3)对不同宽厚比的角钢，临界高厚比随长细比的增加整体呈上升趋势，这一规律不因材料强度的不同而改变。

(4)两边凸起、单边凸起、两边凹陷、单边凹陷这四种局部残余变形形式对角钢的轴压承载力影响相似，均在一定局部变形范围内不会导致承载力下降。因此对有这类损伤的角钢，在评定其轴压承载力时可根据局部变形大小来判断承载力是否下降。

[1] 王奔，郭小农，蒋首超，等.FRP加固金属结构研究综述[J].结构工程师，2012，28(5):183-190.Wang Ben，Guo Xiaonong，Jiang Shouchao，et al.Art state of metal structures strengthened with FRP[J].Structural Engineers，2012，28(5):183-190.(in Chinese)

[2] 章静，毛德灿，万月荣，等.世博会浦西综艺大厅网架改建结构设计[J].结构工程师，2010，26(5):124-129.Zhang Jing，Mao Decan，Wan Yuerong，et al.Grid structure renovation design for Shanghai EXPO performance hall[J].Structural Engineers，2010，26(5):124-129.(in Chinese)

[3] Federal Emergency Management Agency.FEMA-352 Recommended postearthquake evaluation and repair criteria for welded steel moment-frame buildings[S].Guidelines Development Committee，2000.

[4] 中华人民共和国建设部.GB 50017—2003钢结构设计规范[S].北京:中国计划出版社，2003.Ministry of Construction of the People’s Republic of China.GB 50017—2003 Code for design of steel structures[S]. Beijing: China Planning Press，2003.(in Chinese)

[5] 金伟良，宋剑，龚顺风，等.海洋平台受损构件的承载能力与加固分析[J].工程力学，2003，20(5):100-105.Jin Weiliang，Song Jian，Gong Shunfeng，et al.A-nalysis of bearing capacity and strengthening of damaged members for offshore platform[J].Engineering Mechanics，2003，20(5):100-105.(in Chinese)

[6] American Petroleum Institute.RP 2A-WSD Recommended practice for planning，designing and constructing fixed offshore platforms-working stress design[S].American Petroleum Institute，2000.

[7] 中华人民共和国建设部.GB 50292—1999民用建筑可靠性鉴定标准[S].北京:中国建筑工业出版社，1999.Ministry of Construction of the People’s Republic of China.GB 50292—1999 Standard for appraiser of reliability of civil buildings[S].Beijing:China Architecture and Building Press，1999.(in Chinese)