橡胶伸缩缝对连续梁桥地震反应的影响

宋德琴 袁万城

(同济大学土木工程防灾国家重点实验室，上海200092)

1 引言

近年来地震灾害成为地球上多发的自然灾害，令人触目惊心的灾情不仅时时敦促着桥梁抗震设计理论日趋完善，更将国内外地震工作者的目光集中于对震害的调查研究上。国内外地震工作者多年来的研究表明，强震作用下，桥梁的伸缩缝位置处往往出现“碰撞”或“落梁”等震害，对结构安全的破坏极大，甚至破坏生命线工程，影响灾后救灾抢险工作[1-3]。近年来，国内外许多学者致力于研究限位装置以及伸缩缝处“碰撞”现象的发生机理等，很少有人针对伸缩缝开展专门研究，国内现行的一般做法也并不考虑伸缩缝在地震中的作用，规范亦只视伸缩缝为构造措施。为了明确伸缩缝在地震作用下对桥梁的地震反应作用如何，并且考虑到板式橡胶伸缩缝具有简明的传力途径，本文以某城市高架中一座连续梁为背景，在不同的场地条件下研究了橡胶伸缩缝弹性刚度变化对该桥地震反应影响。

2 数值分析模型

2.1 板式橡胶伸缩缝单元

板式橡胶伸缩缝利用图1中1，2部分橡胶的剪切变形来适应桥面的伸缩位移[4]。其结构如图1所示，是一种线弹性伸缩缝，本构关系如图2所示。伸缩缝刚度只计入图1中1，2部分的剪切刚度。普通橡胶剪切刚度的计算公式:

图1 板式橡胶伸缩缝Fig.1 Slab type expansion joint

图2 弹性伸缩缝恢复力特性Fig.2 Resilience characteristic for the elastic expansion joint in the numerical model

图3 全桥计算模型Fig.3 Calculation model of the bridge

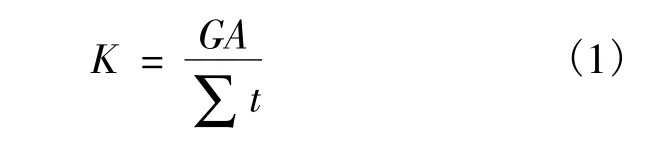
式中，G=1.2 MPa，为橡胶的剪切模量;A为剪切面积;∑t为橡胶层总厚度。

经过计算，桥宽26 m时缝宽80 mm的伸缩缝刚度约为1.5×104kN/m。为研究伸缩缝弹性刚度变化对结构地震反应的影响，将待研究橡胶伸缩缝刚度范围设置为1×104～1×105kN/m，变化间距为1×104kN/m。

2.2 全桥模型的建立

以一座三联连续梁桥(30+45+40+35+40+35+40+45+30)m为背景，上部结构为等截面预应力混凝土连续箱梁结构，桥宽26 m。下部采用等高度双柱式框架墩，不考虑桥台作用，基础均为方形承台下布置钻孔灌注桩。活动墩上采用板式橡胶支座，固定墩上采用固定盆式支座。相邻联之间设置板式橡胶伸缩缝。

Sap2000[5]动力分析模型采用三维空间有限元分析模型，如图3所示。其中，主梁和桥墩采用梁单元模拟(假定桥墩不发生塑性变形)，群桩基础考虑桩基周围土体的约束，采用承台底6个自由度的弹簧刚度模拟桩土相互作用，弹簧刚度值由“m法”计算确定。假设地震作用下固定支座不发生剪坏，故所有支座均采用线性连接单元模拟，将可活动方向弹性刚度设为0、不可活动方向刚度设为1×1011kN/m，以此做简化处理。板式橡胶伸缩缝采用线性连接单元模拟。

3 动力特性分析

分析伸缩缝刚度对结构地震响应的影响，应首先研究桥梁相邻联的动力特性。本文对采用不同伸缩缝刚度的模型进行了动力特性分析。由于文中只考虑沿纵向的地震输入和伸缩缝剪切刚度，故只研究桥梁的纵向动力特性。忽略高阶振型的影响，且考虑到各模型的前十阶振型中均只有前三阶为纵向振型，因此将伸缩缝刚度变化对前三阶周期的影响绘于图4。可以看出，第一阶周期在伸缩缝刚度增加至2×104kN/m后基本不变，而第二、第三阶周期随着伸缩缝刚度增加减小非常显著。同样，模型计入伸缩缝刚度后其纵向振动特点也发生了很大变化。由表1可以看出，不考虑伸缩缝影响时结构前三阶的振动特点分别为第三联、第一联和第二联的独立纵向振动;而在有伸缩缝模型中，结构前三阶振型均表现为三联一起振动，振动特点分别为三联同向纵向平移、第一和第三联相对纵向平移、第二联与第一和第三联不同向纵向平移。

图4 前三阶纵向振型周期Fig.4 Longitudinal periods of the first three modes

表1 无/有伸缩缝模型的振型特点比较Table 1 Comparison of modal characteristics without/with expansion joint

4 地震反应时程分析

4.1 地震动输入

地震输入采用由《城市桥梁抗震设计规范》[6](JJ 166—2011)中地震烈度Ⅷ度区Ⅰ、Ⅱ、Ⅲ、Ⅳ类场地而确定的反应谱曲线拟合的4条人工地震波，地震波的加速度峰值均调整为0.6g。4条地震波分别见图5，阻尼比取5%。横桥向振动不在本文的研究范围内，故地震动仅沿纵向输入。

图5 Ⅰ类、Ⅱ类、Ⅲ、Ⅳ类场地下的人工拟合地震波加速度时程Fig.5 Synthetic seismic waves under different construction conditions of site

4.2 位移响应变化规律

图6所示为第二、三联间相向运动时纵向相对位移最大值(即伸缩缝的纵向压缩变形最大值)随伸缩缝刚度增加的变化情况。如前所述，本文在伸缩缝位置的预留缝隙是8 cm，即当该相对位移大于等于8 cm时可认为相邻联的梁端已经发生碰撞。由图可以看出，在四类场地条件下，不设置伸缩缝时(对应K=0)结构相邻联的相向运动均非常明显，可视结构已经发生碰撞。考虑伸缩缝作用后，相邻联相向运动的纵向相对位移明显减小，并且随着伸缩缝刚度的增加，该位移越来越小，说明伸缩缝对于防止由相邻联相向运动而产生的梁体碰撞效果明显。

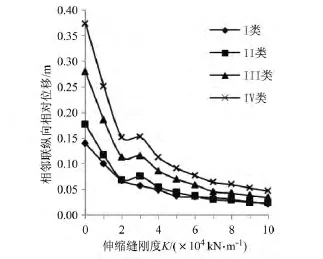
图6 相邻联相向运动纵向相对位移最大值Fig.6 Relative longitudinal displacement betweenthe adjacent beam ends

图7所示为桥梁第二联活动墩(见图3中标示)的墩、梁相对位移最大值随伸缩缝刚度K增加的变化规律。可以看出，在Ⅰ类、Ⅲ类和Ⅳ类场地作用下该相对位随着K增加呈现明显的先减小后增大的规律，且相比同类场地作用下不考虑伸缩缝刚度时(K=0)分别最多减小30%、10%和10%;数据显示，在Ⅱ类场地作用下也有类似的规律，但是变化得不明显，最多减小了5.8%。

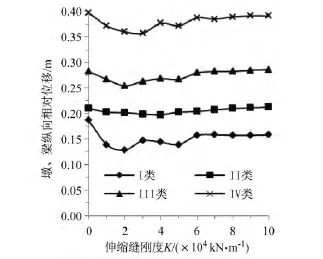
图7 活动墩墩、梁纵向相对位移最大值Fig.7 Relative displacement of the non-fixed pier

4.3 内力响应变化规律

连续梁结构的设计中，一般只设置一个固定墩。地震作用下，纵桥向的地震荷载基本由设置在固定墩上的固定支座来承受，固定墩及其下部基础处于不利的受力状态[7，8]。因此，分析橡胶伸缩缝对结构内力的影响时以固定墩墩底为关键截面，考察其剪力和弯矩变化。由图8可以看出，在不同场地条件下该剪力变化规律不一致:Ⅰ类场地下考虑伸缩缝刚度时固定墩墩底剪力最大值相比K=0时最多约增加25%;Ⅱ类场地下固定墩墩底剪力基本不变;Ⅲ类场地和Ⅳ类场地下该剪力的变化规律类似，均为先增加后逐渐减小，相比各场地条件下K=0时分别最多增加约5.4%和6.1%，最多减小分别4.2%和6.1%。固定墩墩底弯矩变化情况与墩底剪力一致，可见图9，不再赘述。

图8 固定墩墩底剪力最大值Fig.8 Shearing force of the fixed pier

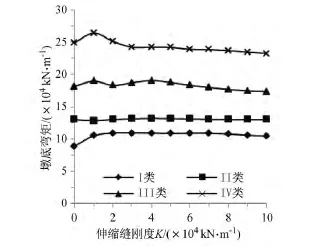
图9 固定墩墩底弯矩最大值Fig.9 Bending moment of the fixed pier

4.4 伸缩缝变形与内力

考虑伸缩缝刚度增加引起的伸缩缝最大变形和最大剪力变化情况，如图10、图11所示。随着伸缩缝刚度增加，伸缩缝的变形不断减小，可以看出伸缩缝刚度较大时这种减小的趋势逐渐变缓，说明伸缩缝刚度增加能控制相邻联的纵向相对位移;而伸缩缝的内力也必然先随之快速增加，当伸缩缝刚度较大时其增加的趋势也相应逐渐减缓。

图10 伸缩缝纵向变形最大值Fig.10 Deformation of expansion joint

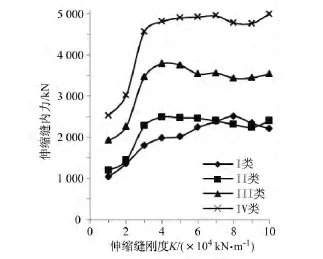
图11 伸缩缝剪力最大值Fig.11 Shearing force of expansion joint

5 结论与展望

为了直观具有弹性刚度的板式橡胶伸缩缝对于连续梁桥的地震反应的影响，本文首先对比分析了无伸缩缝模型和有伸缩缝模型的动力特性，并在四类不同场地作用下研究了伸缩缝刚度变化对其自身的内力与变形、结构相邻联相向运动、墩梁相对位移及墩底内力的影响。研究结果表明:

(1)伸缩缝能减小结构相邻联的纵向基本周期;

(2)伸缩缝刚度增加对于限制由相邻联相向运动产生的碰撞效果明显;

(3)伸缩缝刚度增加可在一定程度上减小墩、梁相对位移，但是伸缩缝刚度持续增加对限制墩、梁相对位移并无明显作用;

(4)在不同场地条件下，伸缩缝发挥限位能力的同时固定墩墩底内力的变化情况并不一致。

因此，在结构设计中可以考虑加强伸缩缝的设计，在满足结构正常使用条件下的位移需求的同时，发挥一定的限位能力;并应保证伸缩缝与梁端的有效连接，以此避免伸缩缝位置在地震作用下成为结构的薄弱环节。

[1] 叶爱君，管仲国，范立础.桥梁抗震[M].北京:人民交通出版社，2012.Ye Aijun，Guan Zhongguo，Fan Lichu.Seismic design of bridges[M].Beijing:China Communications Press，2012.(in Chinese)

[2] 范立础，李建中.汶川桥梁震害分析与抗震设计对策[J].公路，2009，5(5):122-128.Fan Lichu，Li Jianzhong.Seismic damage analysis and design strategy in the Wenchuan earthquake[J].Highway，2009，5(5):122-128.(in Chinese)

[3] 孟杰，刘钊.汶川地震中的桥梁落梁震害分析及启示[J].结构工程师，2010，26(2):95-100.Meng Jie，Liu Zhao.Causation analysis and enlightenment on bridge unseating in the Great Wenchuan earthquake[J].Structural Engineers，2010，26(2):95-100.(in Chinese)

[4] 许楠.板式橡胶伸缩装置的破损机理研究[J].科技论坛，2007，5:22.Xu Nan.Breakage mechanism study of the plate rubber expansion device[J].Science Forum，2007，5:22.(in Chinese)

[5] Computers and Structures Inc.CSI analysis reference manual for SAP 2000[M].Berkeley:Computers and Structures Inc，2004.

[6] 中华人民共和国住房和城乡建设部.CJJ 166—2011 城市桥梁抗震设计规范[S].北京:中国建筑工业出版社，2011.Ministry of Housing and Urban-Rural Development of the People’s Republic of China.CJJ 166—2011 Code for seismic design of urban bridges[S].Beijing:China Architecture and Building Press，2011.(in Chinese)

[7] 郭磊，李建中，范立础.大跨度连续梁桥减隔震设计研究[J].土木工程学报，2006，39(3):81-85.Guo Lei，Li Jianzhong，Fan Lichu.Research on seismic isolation design for long-span continuous bridges[J].China Civil Engineering Journal，2006，39(3):81-85.(in Chinese)

[8] 范立础，王志强.桥梁减隔震设计[M].北京:人民交通出版社，2001.Fan Lichu，Wang Zhiqiang.Seismic isolation design of bridge[M].Beijing:ChinaCommunications Press，2001.(in Chinese)