某商场大跨楼盖竖向振动舒适度分析

曾大明 牛金龙

(1.中国海诚工程科技股份有限公司，上海200031;2.上海市城乡建设和交通委员会科学技术委员会，上海200032)

1 引言

近年来，随着结构分析和施工技术的进步、高强材料的应用，现代建筑结构楼盖变得更轻、更柔，跨度更大。然而，大跨度楼盖结构由于其竖向自振频率较低，在人的正常活动下，很容易发生振动。这些振动虽然不足以使结构出现安全性问题，但是其达到一定程度时会让生活和工作在其上的人感到不舒适，产生紧张甚至恐慌心理，从而直接导致结构舒适度的降低。如果大跨楼盖结构在建成后才发现使用性不能满足舒适度要求而不得不进行后期改造的话，则可能需要花费很大的投入，有时甚至无法施工。因此，在设计阶段就对大跨楼盖结构的竖向振动舒适度进行分析和评估就变得非常重要。

本文针对一个商场建筑工程实例，为满足其使用功能要求，在结构设计阶段，对其大跨楼盖结构的竖向振动舒适度进行了计算分析和评估。

2 楼盖振动的基本概念

2.1 人行激励的荷载模型

楼盖振动的振源主要是人的活动，包括行走、跑动、跳跃等，通常称为人行激励。人行激励下，楼盖的振动表现为强迫振动。由于人行激励可能是单人行走引起，也可能是多人共同活动引起，荷载作用点不断变化，同时受步频和体重等因素的影响，因此评价楼盖振动舒适性，就必须建立人行激励的荷载模型。

研究人行激励荷载模型的切入点是单步落足曲线(单足作用在地面上的竖向作用力与落足时间的关系曲线)。典型的单步落足曲线如图1[1]所示。由于人的重心在行走过程中不断的上升和下降，因此施加给地面一个竖向动力荷载，其大小并不一直等于体重，而是随行走过程上下波动。如图1中，A为人的足跟开始接触地面，然后随人的重心转移曲线逐渐上升，曲线高度到达1.2～1.25倍人的体重时，达到第一个峰值点B，该峰值包括了人的体重和运动惯性力的总和。随后，随着人屈膝、摆动另一条腿以及重心的转移，该曲线下降至C点，C点的力一般要小于人的体重。接着人的脚掌蹬地，使得该曲线再次升高至D点，D点作用力的大小约为人体重的1.15倍。D点以后，曲线迅速下降至E点，此时人的足尖完全离开地面。单步落足曲线的形式也与人行进时的状态有关，图2[2]给出了多种不同行进状态下的单步落足曲线形式。

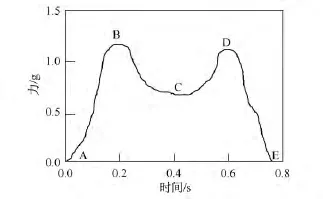
图1 单步落足曲线[1]Fig.1 Single-step walking load pattern[1]

人的行走由连续的单步组成，具有周期性，步频一般在1.5～2.5 Hz之间。根据单步落足曲线，假定人左右两脚产生的单步落足曲线相同，就可以定义出一条完整的行走激励曲线。历史上许多研究者给出了简化的步行曲线。例如，Allen和Rainer通过对单人和多人连续行走产生的动力荷载进行研究，提出单人行走的荷载可以表示为人的体重加上一个周期性分量[3]:

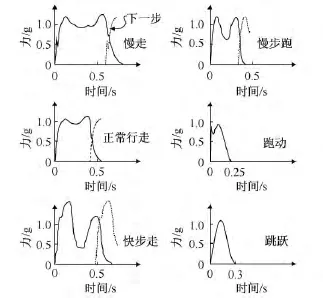
图2 多种行进状态单步落足曲线[2]Fig.2 Detailed forcing patterns for various modes of walking， jogging and running(after Wheeler，1982)[2]

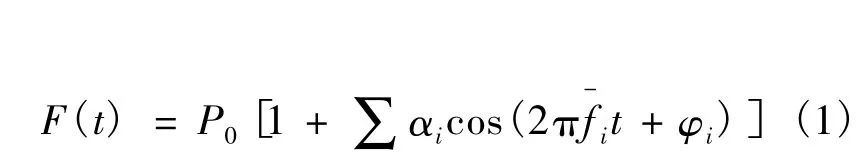
式中 P0——人的体重;

αi——第i阶荷载频率动力因子;

fi——第 i阶荷载频率;t——时间;

φi——第i阶荷载频率相位角。对于大型商场等场所，参与行走运动的人数一般较多，与单人行走荷载有较大差异，不能用单个集中荷载来模拟。传统上，一般用等效均布动荷载来反映其对楼盖体系振动的影响。等效均布动荷载的大小取决于参与行走运动的人数。根据人的体重和单位面积的人数得到的等效均布动荷载与单人行走的荷载类似，可表示为[3]

式中 wp——人的等效均布荷载;αi——第i阶荷载频率动力因子;

t——时间;

φi——第i阶荷载频率相位角。

2.2 楼盖舒适度动力特性

2.2.1 质量

楼盖体系的质量与其上的荷载取值有关，而需要特别说明的是，楼盖舒适度计算中的荷载取值不同于一般结构设计。舒适度计算中的荷载取值需要考虑恒荷载和有效均布活荷载。恒荷载应取实际楼盖体系上的荷载(包括楼盖、面层以及装修等荷载)，而不是设计恒荷载。有效均布活荷载指楼盖上随机布置的家具、设备等的均布重量。比如，就办公楼来说，主要考虑桌椅、文件柜等的重量，一般取0.5 N/m2;就住宅楼来说，主要考虑家具等的重量，相对较轻，一般取0.3 N/m2;对于商场这类大空间建筑来说，由于空间大，家具较少，有效均布活荷载的数值较小，可忽略不计。由此可见，舒适度计算中恒荷载的取值要比结构设计的设计恒荷载小，有效均布活荷载也不同于结构设计时的均布活荷载，要小得多。

2.2.2 自振频率

楼盖的舒适度研究，主要是指楼盖的竖向振动，竖向振动对应的自振频率为竖向自振频率。对于形状规则、质量分布均匀、边界条件简单的楼盖体系，其第一阶振动起控制作用，因此可以等效为单自由度体系，采用单自由体系的分析方法计算其竖向自振频率。对于较复杂的楼盖体系，可采用多自由度计算模型，通过整体建模分析得到其各阶竖向自振频率。

2.2.3 阻尼

楼盖结构体系的阻尼包括结构构件的阻尼及非结构构件的阻尼。对于人行激励的情况，钢结构楼盖的阻尼一般可取0.02，混凝土楼盖的阻尼可取0.05，对于钢—混凝土组合楼盖的阻尼可取0.06，轻型框架的阻尼可取 0.12。

2.3 楼盖体系振动分析模型

楼盖体系的振动分析模型主要有共振模型和局部变形模型两种。

首先，不论是人行走、跑动或是有节奏的运动，都可近似为一系列简谐荷载的组合，因此简谐力是人行激励的基本特征。当人行激励荷载的频率与楼盖的自振频率相同或相近时，楼盖的振动峰值达到最大。共振模型是预测人行激励下楼盖体系振动的基础模型。

对于轻钢结构等轻型框架结构，其自振频率较高，人对振动的不舒适感主要来自于人行走时楼盖因局部较大变形引起的晃动。因此，对于自重较轻、自振频率较高的轻型框架结构的楼盖体系，振动设计更多的是保证集中荷载作用下楼盖的局部刚度。

2.4 楼盖振动舒适度评价标准及计算方法

目前国内外规范标准对于楼盖舒适度的评价和控制主要从挠度、频率和加速度三个方面。

用挠度去评价楼盖舒适度主要用于钢结构，其来源是基于楼盖体系振动分析模型中的局部变形分析模型。比如，我国《钢结构设计规范》以及美国钢结构标准中均有对钢结构构件在可变荷载标准值作用下的挠度与跨度比值进行限制的规定。

以频率和加速度去评价楼盖振动舒适度，其本质均是基于楼盖体系分析模型中的共振分析模型。其思路是使楼盖结构体系的自振频率避开人行荷载频率，避免楼盖结构体系在人行激励下产生共振，进而避免较大振动加速度的发生。我国《混凝土结构设计规范》明确给出了对大跨混凝土楼盖竖向自振频率的限值要求[4];我国《高层建筑混凝土结构技术规程》也明确给出了大跨楼盖竖向振动加速度的限值要求[5]。表1列出了常用的舒适度评价规范标准及其控制参数[6]。

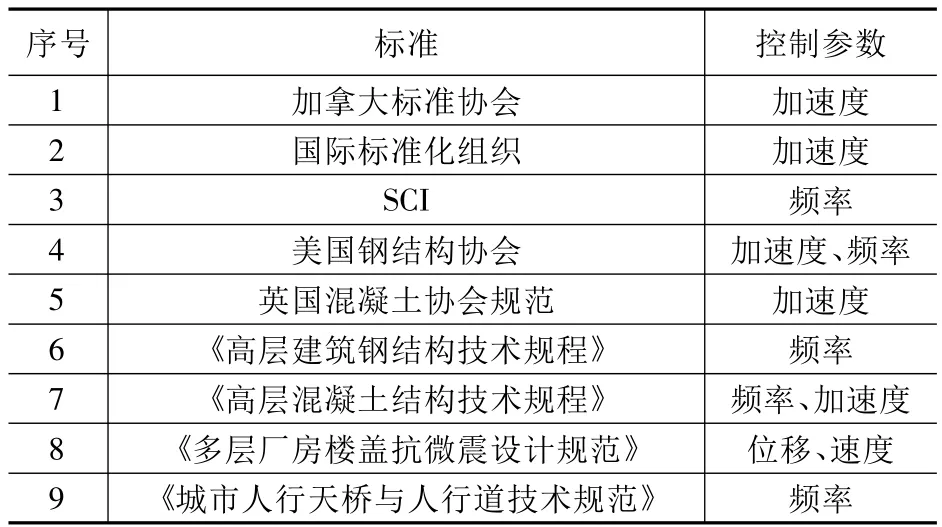
表1 大跨楼盖竖向振动舒适度标准分类[6]Table 1 Classification of design criteria for vibration serviceability of long-span floor[6]

对于楼盖振动舒适度的计算主要有简化计算法和有限元分析法。对于结构布置相对简单、规则的楼盖结构，可以快速求出楼盖体系的自振频率，然后根据相关简化计算公式求得楼盖体系的振动加速度，据此判断楼盖体系的舒适度。对于复杂的楼盖体系可以整体建模采用有限元分析进行楼盖舒适度的计算。

3 楼盖竖向振动舒适度计算

3.1 工程概况

本工程为江苏省常州市某一大型家具商场，为现浇钢筋混凝土框架结构，地上4层，底层层高4.5 m，其他层层高4.0 m。结构整体模型如图3所示。

图3 结构整体模型Fig.3 Structure model

结构典型柱网尺寸为9 m×15 m，具体梁、板尺寸信息见图4。混凝土强度等级为C30，钢筋强度等级为HRB400。

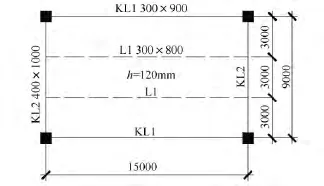
图4 楼盖结构尺寸Fig.4 Dimensions of slab-structure

3.2 楼盖竖向振动舒适度计算

由于该建筑标准层楼板的结构布置均匀对称，主梁刚度较大，属于单向梁板式楼板，一般可以忽略柱、板、主梁的挠度和变形，因此可仅考虑次梁的挠度取一跨典型楼板(图4)采用简化计算法进行舒适度计算。

计算时，认为次梁与主梁铰接。在计算次梁惯性矩 I时，参照《混凝土结构设计规范》[4]5.2.4条确定梁受压区有效翼缘宽度，考虑楼板对对梁刚度的增大作用。楼盖竖向振动加速度计算参照我国《高层建筑混凝土结构技术规程》附录A中相关公式。计算过程如下:

次梁上均布线荷载:q=21.00 kN·m。

3.2.2 有限元分析法

表2 楼板体系荷载Table 2 Loads on the slab kN·m－2

3.2.1 简化计算法

选取结构中一整层楼盖为研究对象，利用Midas/Gen软件建立有限元模型(图5)进行步行激励作用下的楼盖振动时程分析。其中，梁、柱构件使用梁单元，并假设柱的上、下端为固定端。楼盖采用板单元，并在将要施加动力荷载的位置按人行走时的步距75 cm进行单元划分和节点建立，这样就可在行走路径对应的节点上按时间顺序依次施加和消除步行激励。用于时程分析的步行荷载模型选用Midas/Gen软件提供的IABSE(International Association for Bridge and Structure Engineering)模型(图6)。人体自重取75 kg，步频取2 Hz。结构阻尼比取0.05。

图5 计算模型Fig.5 Calculation model

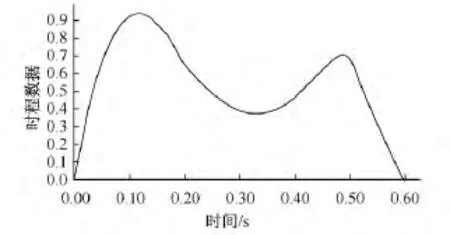
图6 IABSE步行荷载模型Fig.6 Single-step walking load pattern of IABSE

具体计算工况介绍如下:

工况1:单人步行，即假定单人在楼盖上沿最不利路径行走的情况。单人步行路径如图7所示。

工况2:等效均布步行，即假定在楼盖上沿商场的主要顾客步行通道(不包括储货区、柜台区等人行较少的区域)按每平米一定人数同时行走的情况。由于目前还没有专门针对商场建筑舒适度方面的规范标准，本文在确定单位面积参与行走人数时参考《美国道路通行能力手册》(HCM2000)中的相关规定，见表3。假定商场中人行走的状态与表3中的B级相近，按0.4人/m2布置人步行荷载，人行激励加载点布置如图8所示。

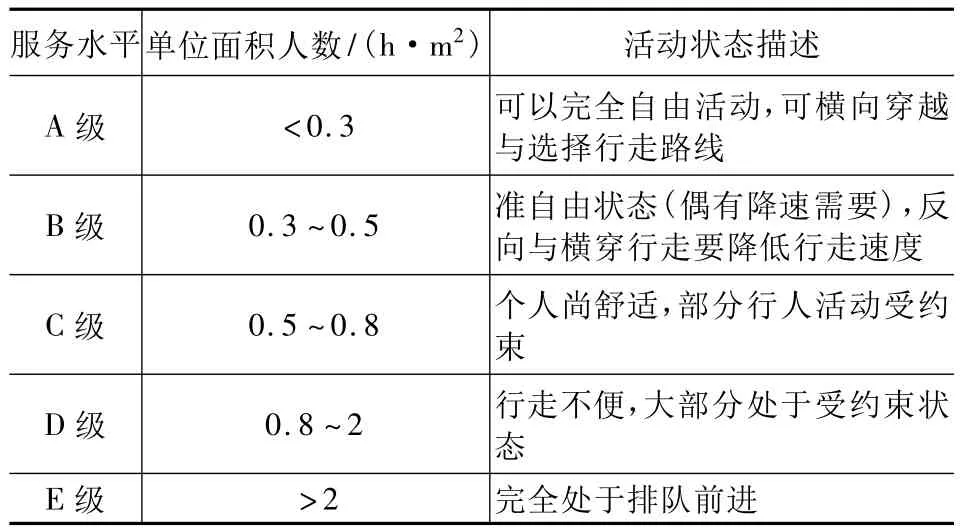
表3 人行道服务水平标准[3]Table 3 Pavement service level standard[3]

图7 单人步行路径(工况1)Fig.7 Single-person walking path

图8 等效均布步行路径(工况2)Fig.8 Uniformly distributed equivalent-walking path

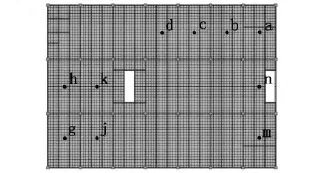
图9 加速度输出分布点Fig.9 Layout of acceleration-output points

图10 楼盖竖向振动模态Fig.10 Vertical vibration frequency of floor-slab

3.3 计算结果分析

综合以上两种计算方法得出的计算结果，该商场大跨混凝土楼盖结构的自振频率大于3 Hz，竖向加速度反应峰值不大于0.015 g，满足我国混凝土结构设计规范和高层混凝土结构设计规程中对于楼盖自振频率和加速度反应的限值规定，因此，该商场大跨楼盖竖向振动舒适度基本能满足要求。

从计算过程可以看出，简化计算法计算结果主要受结构本身固有特性、荷载大小等影响，不能充分灵活地反映楼盖边界条件、步行荷载特性(如荷载模型、加载频率、作用位置等)以及加载模式等因素的影响。简化计算法计算假定类似于有限元法工况1(单人步行工况)，因此二者计算结果较接近，但均远小于有限元法工况2(等效均布步行工况)的计算结果，而有限元法工况2更符合商场中步行激励的最不利工况。因此，简化计算法对于商场这种人流分布较广且随机的情况下的舒适度计算不适于采用。

图11 楼盖竖向加速度反应(工况1)Fig.11 Vertical acceleration response of floor-slab(condition 1)

图12 楼盖竖向加速度反应(工况2)Fig.12 Vertical acceleration response of floor-slab(condition 2)

由有限元法工况1计算结果可以得出:边跨的竖向振动反应大于中间跨，洞口附近的楼盖竖向振动反应大于远离开洞区域楼盖，说明楼盖边界条件的强弱对楼盖竖向振动有较大影响。

对比有限元法两种荷载加载工况的计算结果可以得出，等效均布步行加载模式下的楼盖竖向振动加速度反应峰值要远大于单人步行加载模式，反映了步行荷载加载模式对于楼盖竖向振动的影响。

4 结论

本文对某商场大跨楼盖体系的竖向振动舒适度进行了计算分析和评估，从中得出:

(1)该商场大跨楼盖体系的频率和加速度反应均能基本满足我国规范的限值要求，因此其竖向振动舒适度基本能满足要求。

(2)楼盖竖向振动舒适度受其边界约束条件影响较大。例如，剪力墙对楼盖约束较大，其附近楼盖舒适度较容易满足;边跨楼盖竖向振动舒适度相对于中间跨较不利;洞口对楼盖竖向振动舒适度也较为不利。

(3)楼盖结构的刚度宜均匀布置。为满足某一跨楼盖的竖向振动舒适度要求而单纯加强该跨楼盖的刚度会造成竖向振动不利点向相邻跨刚度较弱楼盖转移。

(4)步行荷载激励下，最大位移一般发生在楼盖中央，但最大加速度却未必会发生在相同位置，比如出现在楼盖次梁位置。

(5)荷载加载方式，直接影响楼盖体系的自振频率，进而影响楼盖振动的加速度响应，应进一步仔细研究。

(6)相关标准规范中的简化计算公式不能精确反映诸如楼盖边界条件、步行荷载模式以及加载方式等方面的影响，因此，对于楼盖结构体系的竖向振动舒适度计算，宜采用有限元法整体建模计算。

[1] 虞终军，丁洁民，阮永辉，等.超高层建筑办公楼面竖向振动舒适度分析[J].结构工程师，2012，28(1):14-20.Yu Zhongjun，Ding Jiemin，Ruan Yonghui，et al.Floor vibration serviceability analysis of a high-rise of-fice building[J].Structural Engineers.2012，28(1):14-20.(in Chinese)

[2] Aleksandar P，Reynolds P.Vibration serviceability of long-span concrete building floors:part 1-review of background information[J].The Shock and Vibration Digest，2002:75-76.

[3] 娄宇，黄健，吕佐超.楼盖体系振动舒适度设计[M].北京:科学出版社，2012.Lou Yu，Huang Jian，Lu Zuochao.Vibration comfort design of floor-slab system[M].Beijing:Science Press，2012.(in Chinese)

[4] 中华人民共和国建设部.GB 50110—2010混凝土结构设计规范[S].北京:中国建筑工业出版社，2011.Ministry of Construction of the People’s Republic of China.GB 50110—2010 Code for design of concrete structures[S].Beijing:China Architecture and Building Press，2011.(in Chinese)

[5] 中华人民共和国建设部.JGJ 3—2010高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社，2011.Ministry of Construction of the People’s Republic of China.JGJ 3—2011 Technical specification for concrete structures of tall building[S].Beijing:China Architecture and Building Press，2011.(in Chinese)

[6] 折雄雄，陈隽.大跨度楼盖振动舒适度研究综述[J].结构工程师，2009，25(6):144-149.She Xiongxiong，Chen Jun.A review of vibration serviceability for long-span floors vibration serviceability analysis of a high-rise office building[J].Structural Engineers，2009，25(6):144-149.(in Chinese)