反复荷载作用下钢筋混凝土柱的非线性分析
2014-06-28高向玲张元达
高向玲 张元达
(同济大学建筑工程系,上海200092)
1 引言
钢筋混凝土柱作为混凝土框架结构及桥梁结构的主要承重构件,在地震作用下表现为显著的弹塑性受力特性。准确预测地震作用下钢筋混凝土柱的受力性能及其震后残余变形,对评估结构的震害程度和安全性具有重要意义。
研究者对钢筋混凝土柱进行了大量的研究。Lee 和 Elnashai[1]基于纤维单元程序 ADAPTIC,对弯剪作用下钢筋混凝土柱的滞回性能进行了模拟分析;Esmaeily和Xiao[2]基于纤维单元模型编制了桥墩的滞回分析程序;龙凌等[3]基于ANSYS对外包钢筋混凝土加固钢筋混凝土柱进行了有限元分析;高利军等[4]基于ABAQUS对考虑约束混凝土的RC柱的承载力进行了研究。
本文分别采用ABAQUS和OpenSEES两种不同的有限元分析软件对一根钢筋混凝土柱在反复荷载作用下的受力性能进行了模拟,并与试验结果进行了对比,比较了两者的异同。
2 基于ABAQUS的数值模拟
2.1 混凝土损伤塑性模型简介
ABAQUS提供的混凝土损伤塑性模型是依据Lubliner[5],Lee 和 Fenves[6]提出的损伤塑性模型确定的,其目的是为分析在循环加载和动态加载条件下混凝土结构的力学响应提供普适的材料模型,它考虑了材料拉压性能的差异,主要用于模拟低静水压力下由损伤引起的不可恢复的材料退化。这种退化主要表现在材料宏观属性的拉压屈服强度不同、拉伸屈服后材料表现为软化及压缩屈服后材料先硬化后软化、拉伸和压缩采用不同的损伤和刚度折减因子、在循环荷载作用下,刚度可以部分恢复等。
2.2 混凝土应力-应变关系
采用损伤塑性模型时,需要计算混凝土应力、非弹性应变和损伤因子,本文采用《混凝土结构设计规范》[7](GB 50010—2010)(下文简称为《规范》)推荐的混凝土应力-应变骨架曲线计算损伤塑性模型中所需的参数。
2.2.1 混凝土受拉应力-应变关系
《规范》建议的混凝土单轴受拉应力-应变关系表达式见式(1)—式(3)。

式中,αt为混凝土单轴受拉应力-应变曲线下降段的参数值;ft,r为混凝土的单轴抗拉强度代表值;εt,r为与单轴抗拉强度 ft,r相应的混凝土峰值拉应变。
由于KEEL试验室提供的试验柱的混凝土立方体抗压强度实测值为35.7 N/mm2,其抗拉强度ft,r近似取立方体抗压强度的十分之一,即3.5 N/mm2,弹性模量 Ec取 2.8 × 1010N/m2,查《规范》得 εt,r=128 ×10-6,αt=3.82。混凝土受拉本构相关参数取值如表1所示。2.2.2 混凝土受压应力-应变关系
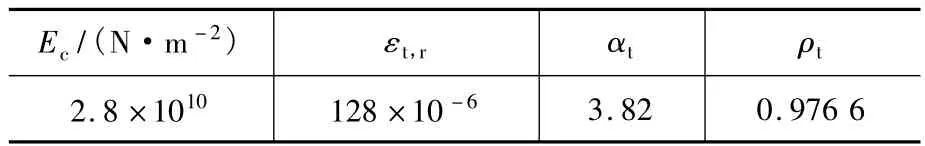
表1 混凝土受拉本构参数Table 1 Paraneters of concrete for tension
《规范》建议的混凝土单轴受压应力-应变关系表达式见式(4)—式(7)。

式中,αc为混凝土单轴受压应力-应变曲线下降段的参数值;fc,r为混凝土的单轴抗压强度代表值;εc,r为与单轴抗拉强度 fc,r相应的混凝土峰值压应变。
本文中 fc,r取 35 × 106N/mm2,Ec取 2.8 ×1010N/m2,查《规范》求得 εc,r=1 720 × 10-6,αc=1.65。混凝土受压本构相关的参数取值如表2所示。

表2 混凝土受压本构参数Table 2 Parameters of concrete for compression
2.2.3 损伤因子的确定
本文采用基于能量损失的方法来计算损伤因子。按照Najar的损伤理论[8],脆性固体材料的损伤定义为

式中,W0为无损材料的应变能密度,且

式中,E0为无损材料的四阶弹性系数张量;E为损伤材料的四阶弹性系数张量;ε为相应的二阶应变张量;ΔWε表示无损材料的应变能密度W0与损伤材料的应变能密度Wε之差。
对于混凝土单轴受压的一维受力状态,可得

式中,W0和Wε分别为混凝土应力-应变关系图(图1)中三角形OAB和阴影部分的面积。

图1 基于能量损失的损伤模型Fig.1 Energy loss-based damage model
根据式(14),只要知道混凝土的受压或者受拉应力-应变关系,将阴影部分面积分解成若干个梯形面积之和,运用Matlab编制相应的计算程序,即可得出阴影部分的近似面积。
本文采用《规范》推荐的混凝土应力-应变骨架曲线计算损伤因子。混凝土受拉上升段简化为直线,不考虑损伤;混凝土受压考虑全过程损伤。非弹性应变根据下式求得:
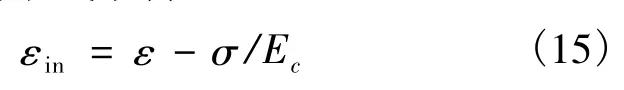
通过计算得到受拉损伤因子Dt和受压损伤因子Dc随非弹性应变的变化曲线分别如图2和图3所示。

图2 受拉损伤因子-非弹性应变关系Fig.2 Tensile damage factor vs inelastic strain

图3 受压损伤因子-非弹性应变关系Fig.3 Compression damage factor vs inelastic strain
从图2和图3中可以看出,损伤因子均随着非弹性应变的增加而增加,并且趋于1;随着非弹性应变的增加,损伤因子的增长速率逐渐减小。
2.2.4 损伤塑性模型参数
1)混凝土受压刚度恢复系数wc
此参数表示混凝土从受拉状态转入受压状态时混凝土材料的抗压刚度恢复程度。由于本试验是对柱端施加低周反复荷载,混凝土会经历拉、压的反复作用,故此参数在模拟中显得尤为重要。当wc=0时表示材料不能恢复刚度;当wc=1时,则表示材料完全恢复抗压刚度;当wc在0~1之间时,则表示刚度只能部分恢复,如图4所示。经过反复试算,文中取wc=0.3。
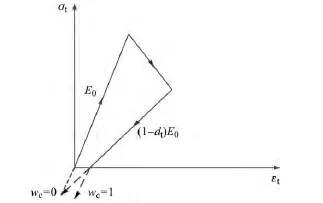
图4 受压刚度恢复系数Fig.4 Recovery coefficient of compression stiffness
2)其他参数
混凝土损伤塑性模型其他相关的参数还包括:Ψ为膨胀角,μ为黏性系数,∈为流动势偏移值,αf为双轴极限抗压强度与单轴极限抗压强度的比值,Kc为拉伸子午面与压缩子午面上第二应力不变量之比。各参数取值如表3所示。

表3 混凝土损伤塑性模型参数Table 3 Parameter of concrete damage plastic model
2.3 钢筋本构模型
钢筋本构模型采用PQ-Fiber中的USTEEL02模型[9]。PQ-Fiber是清华大学土木工程系基于ABAQUS开发的一组材料单轴滞回本构模型的集合,其中的USTEEL02本构模型是一种再加载刚度按Clough本构退化的随动硬化单轴本构模型。
该模型如图5所示,其主要特点是在反向再加载时,并不立即指向历史最大点(εmax,fmax),而是先按卸载刚度加载至历史最大点对应应力的0.2倍,即0.2fmax,再指向历史最大点。此模型定义的强度退化模型考虑累积损伤引起的钢筋混凝土构件的受弯承载力退化,可采用表达式(16)表示如下:
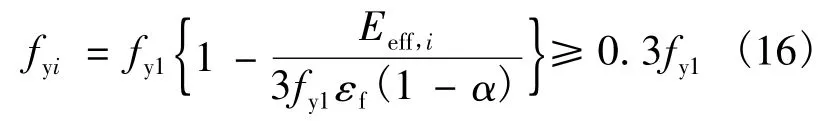
式中,fyi表示第i个加载循环的屈服强度,正负号分别表示正向或反向加载;α为屈服后刚度系数;Eeff,i表示加载至第i个循环时的有效积累滞回耗能,将最大响应和滞回耗能两个物理量结合在一起,在累积滞回耗能相等的情况下,较小位移幅值下的承载力退化程度小于较大位移幅值下的承载力退化程度。

图5 反向再加载规则Fig.5 Rule of inverse loading

式中,Ei为第i个循环的滞回耗能;εi为第i个循环所达到的最大应变;εf为钢筋混凝土构件在单调加载下达到破坏时的受拉钢筋应变。
该模型中,钢筋屈服强度的退化以及骨架曲线的下降并非仅考虑钢筋本身的劣化,而是综合反映了钢筋混凝土界面的粘结滑移以及混凝土保护层剥落等引起的综合退化效果。
2.4 有限元模型建立
2.4.1 试件尺寸及配筋
本文采用Kawashima Earthquake Engineering Laboratory数据库[10]里的第一组数据的 TP-2作为研究钢筋混凝土柱数值模拟的对象,柱基本信息如表4所示,柱截面尺寸及配筋分别如图6和图7所示。

表4 钢筋混凝土柱信息Table 4 Information of reinforced conerete column
2.4.2 模型建立
共创建三个分析步,初始分析步施加柱底固端约束;分析步一施加柱顶荷载,模拟中为了消除集中荷载的影响,将柱顶力简化为均布荷载,取为981 250 Pa;分析步二采用位移加载模式,在柱顶端施加低周反复荷载。为了消除加载端的应力集中,在水平加载处设置了刚度较大的垫块,如图8所示。

图6 试件尺寸及配筋图Fig.6 Dimension and reinforcement of testing element
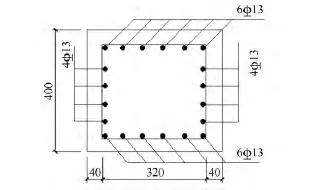
图7 截面配筋图Fig.7 Reinforcement of cross section

图8 柱子模拟图Fig.8 Diagram of column
混凝土采用缩减积分实体单元C3D8R,钢筋采用桁架单元 T3D2,进行分离式建模,采用ABAQUS软件自带的Embed技术,将钢筋嵌入到混凝土中,共同受力。
2.4.3 加载制度
本文进行低周反复的位移加载制度下柱的受力模拟,加载制度如图9所示。

图9 位移加载模式Fig.9 Loading mode of displacement
2.4.4 应力云图
ABAQUS程序分析的结果如图10、图11所示。从图10中可以看出,混凝土柱的底部区域应力最大,破坏从柱底部区域开始发展,符合试验现象描述。图11中柱和基础相交处的底部箍筋所受应力大部分达到屈服强度。2.4.5 数值模拟结果与试验结果比较

图10 混凝土应力云图Fig.10 Stree distribution of concrete

图11 钢筋应力云图Fig.11 Stree distribution of reinforcement
如图12所示。从图中可以看出:①滞回环骨架曲线峰值强度低于真实值,初始刚度略大于真实值;②数值模拟所得的滞回环整体趋势与真实情况吻合较好;③模拟的滞回环骨架曲线呈下降趋势,反映了钢筋混凝土柱加载后期的软化行为。

图12 模拟结果与试验数据对比Fig.12 Comparison of numerical simulation and experimental data
3 基于OpenSEES的数值模拟
OpenSEES采用纤维模型建模,纤维模型是指将纤维截面赋予梁柱构件,即定义构件的每一截面为纤维截面。纤维截面是将构件截面划分成很多小纤维,包括钢筋纤维和混凝土纤维,对每一根纤维只考虑它的轴向本构关系,且各个纤维可以定义不同的本构关系。纤维模型中,假定构件的截面在变形过程中满足平截面假定。
3.1 单元选择
文中采用OpenSEES中的dispalcement-based beam column element单元,该单元允许刚度沿杆长变化,首先通过节点位移得到相应的单元杆端位移,然后根据位移插值函数求得截面的变形,再根据截面的恢复力模型得到相应截面抗力与截面切线刚度矩阵,最后按照Gauss-Legendre积分方法计算出整个截面抗力与切线刚度矩阵。
3.2 混凝土本构模型
混凝土采用OpenSEES中的Concrete01本构模型。为了考虑箍筋约束作用,截面核心区混凝土采用Mander模型[11]确定材料参数。


Mander模型的表达式如式(18)、式(19)所示。式中和εcc为约束混凝土的峰值应力及其对应的应变;fco'和εco为非约束混凝土的峰值应力及其对应的应变;为混凝土的割线模量;为混凝土的切线模量。
考虑箍筋约束修正后的混凝土各参数取值如表5所示。

表5 约束混凝土本构参数取值Table 5 Parametor of constrained concrete
3.3 钢筋本构模型
钢筋采用OpenSEES中的Steel02模型,该模型为双折线模型,可反映钢筋的包兴格效应,如图13所示,模型表达式如式(20)—式(23)所示。式中,σ0和ε0表示双线性包络线屈服点处钢筋的应力和应变;σr和εr表示双线性包络线反向点处钢筋的应力和应变;b为钢筋的硬化刚度和原点切线刚度的比值;R,a1和a2为材料常数;ξ为塑性应变的绝对值。各参数取值见表6。
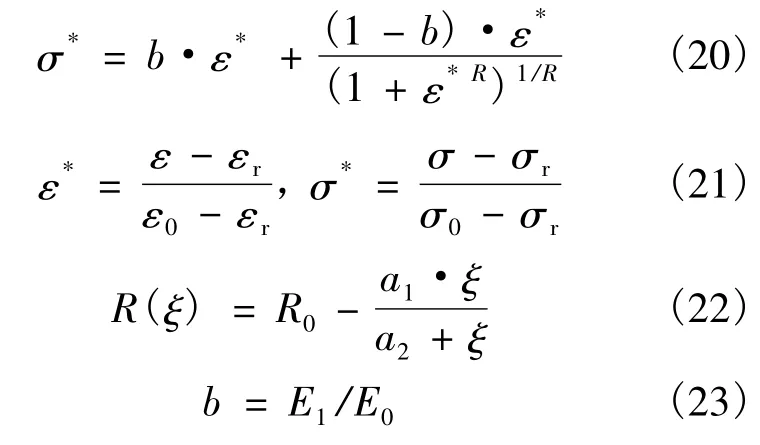

图13 Steel02本构模型Fig.13 Steel02 constitutive model

表6 钢筋本构参数取值Table 6 Parameter of steel constitutive model
3.4 模型建立
整根柱沿柱高划分为四个单元。每个单元纤维截面示意图如图14所示。核心区混凝土划分数为10×10,采用约束混凝土本构;保护层混凝土划分数为10×1和8×1,采用非约束混凝土本构。

图14 纤维截面简化示意图Fig.14 Schematic drawing of a fiber element cross-section

图15 模拟结果与试验数据对比Fig.15 Comparision between numerical simulation and testing results
OpenSEES模拟结果与试验数据的对比如图15所示。从图中可以看出:①采用OpenSEES模拟时,滞回环骨架曲线峰值强度与真实值较接近,初始刚度略大于真实值;②数值模拟所得的滞回环中,除了第一个和后三个滞回环,其他几个滞回环与真实情况吻合较好;③滞回环骨架曲线在后期呈现上升趋势,不能反映钢筋混凝土柱加载后期强度软化的现象;④模拟结果较好地反映了滞回曲线的捏拢现象,与真实情况较接近。
4 讨论
(1)图15中,除了第一个和后三个滞回环,其他几个滞回环与真实情况吻合较好,几乎一致,与ABAQUS模拟结果相比,能更好地符合真实情况。其原因可能是由于OpenSEES采用纤维单元建模,而ABAQUS采用实体单元建模。虽然三维实体有限元模型可以准确地模拟一些重要的非线性行为,但是这种模型的使用是有限制的,计算成本远高于纤维模型,同样的钢筋混凝土柱,用纤维单元分析只需3分钟左右,而实体单元分析却需要大约2小时。相比之下离散纤维模型从内部纤维的本构关系出发,可以有效地模拟复杂的非线性行为,例如损伤导致的刚度和强度退化。由于将构件截面划分成纤维,其位置、截面面积和材料的单轴本构关系都由用户定义,可以运用到各种截面形状。同一截面不同纤维,可以采用不同的单轴本构关系,例如可以分别考虑保护层混凝土和核心区约束混凝土。
(2)OpenSEES中钢筋本构模型采用的是Steel02模型,该模型虽然反映了钢筋的包兴格效应,但是并没有体现钢筋在低周反复荷载下的低周疲劳效应和断裂破坏,因此在图15中,滞回环的骨架曲线在加载后期呈现上升趋势。
5 结语
本文选用了低周反复荷载下的钢筋混凝土柱进行数值模拟,分别采用了ABAQUS实体单元建模和OpenSEES纤维单元建模,并将其同试验结果进行了对比,显然OpenSEES模拟所得结果要好于 ABAQUS所得结果,且计算成本远低于ABAQUS。故对于本文中的钢筋混凝土柱,推荐使用OpenSEES纤维模型。
[1] Lee D H,Elnashai A S.Seismic analysis of RC bridge columns with flexure-shear interaction [J].Journal of Structural Engineering,ASCE,2001,127(5):546-553.
[2] Asadollah E G,Xiao Y.Seismic behavior of bridge columns subjected to various loading patterns[R].PEER 2002/15,Pacific Earthquake Engineering Research Center,Berkeley,CA,2002.
[3] 龙凌.外包钢筋混凝土加固钢筋混凝土柱的有限元分析[D].武汉:华中科技大学,2007.Long Ling.Finite element anatysis on reinforced concrete columns strengthened with Enclosed reinforced concrete[D].Wuhan:Huazhong University of Science and Technology,2007.(in Chinese)
[4] 高利军.基于约束混凝土的RC柱承载力加固研究[D].重庆:重庆大学,2012.Gao Lijun.Study on bearing capacity of strengthened reinforced concrete columns based on confinement mechanisin[D].Chongqing:Chongqing University,2012.(in Chinese)
[5] Lubinerj,Oliver J.et al.A plastic-damage model for concrete[J].International Journal of Solids and Structures,1989,25(3):229-326.
[6] Lee J,Fenves G L.Plastic-damage model for cyclic loading of concrete structures[J].Journal of Engineering Mechanics,1998,124(8):892-900.
[7] 中华人民共和国建设部.GB 50010—2002混凝土结构设计规范[S].北京:中国建筑工业出版社,2007.Ministry of Construction of the People’s Republic of China.GB 50010—2002 Code for design of concrete structures[S].Beijing:China Architecture and Building Press,2007.(in Chinese)
[8] Krajcinovic D,Silva G.Statistic aspects of the continuous damage theory[J].International Journal of Solids and Structures,1989,18(17):551-562.
[9] http://www.collapse-prevention.net/show.asp?ID=14&adID=2.
[10] http://nisee.berkeley.edu/spd/search.html.
[11] Mander J B,Priestley M J N,Park R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,ASCE,1988.
