农民纯收入影响了农业物质要素投入产出弹性吗——基于江苏地区面板数据的门槛模型分析<br/>

农民纯收入影响了农业物质要素投入产出弹性吗——基于江苏地区面板数据的门槛模型分析

2014-06-28张宇青周应恒易中懿

当代经济科学 2014年2期

张宇青，周应恒，易中懿，尹燕

(1.南京农业大学经济管理学院，江苏南京210095;2.江苏大学，江苏镇江212013;3.南京农业大学人文社会科学学院，江苏南京，210095)

一、引言

农业是国民经济的基础产业，自改革开放以来，党中央出台了多项支持农业经济发展的政策，特别是自2004年至今连续10年一号文件接连提出了免除农业税、发展科技农业、建设社会主义新农村、加大农业基础设施建设、完善农村基本经营制度等政策主张，这些都极大促进了农业经济的快速发展。江苏作为我国经济发达地区之一，近年来在率先实现农业现代化的进程中取得了丰硕成果，如通过农机购置补贴政策的实施大力提升了全省农业机械化水平，目前全省农业生产综合机械化水平达70%以上;采取惠农政策促使粮食产量九连增，根据新华网江苏频道报道:2012年全省农业科技贡献率62.3%，比全国平均高8个百分点，粮食单产421.3公斤，比2011年增6.7公斤，其中因单产提高带来的粮食增产量达10.7亿斤，占增产总量的83%［1］;截止2012年1月，江苏高效农业、设施农业占耕地面积比重分别为42.8%和12.2%。农林牧副渔业总产值从2004年的2417.63亿元，增加到2011年的5237.45亿元(图1)，经计算2004-2011年间的几何平均增速为10.46%。

在农业产出和增长的影响因素问题上，多年来众多学者从各个角度展开了分析。吴玉鸣使用空间计量模型分析了我国各省农业生产的空间分布模式和空间依赖性，认为我国省域农业产出空间分布存在局域集聚特征，并且劳动、资本的投入产出弹性很大，而土地贡献不显著［2］;林玉芯基于C-D函数测定了固定资产、劳动力和耕地面积对福建农业经济增长的贡献［3］;党超(2011)使用个体固定效应模型和脉冲响应函数方法对省际面板数据进行分析，认为影响农业产出的各项要素投入的作用大小依次为:农机总动力、用电量、灌溉面积、化肥使用量［4］。上述研究均是从农业生产过程中的各项要素投入出发，利用不同的计量模型对农业要素投入产出弹性进行测算。

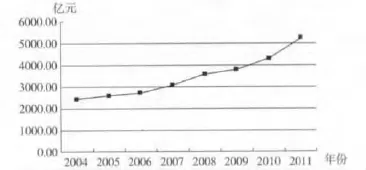
图1 江苏农林牧副渔业总产值序列(2004-2011)

还有一些学者考虑了制度变更、科技发展、对外贸易、金融支持对农业经济的影响，乔榛等人就1978-2004年的土地制度、财税制度变化对农业增长的作用进行检验，认为农业制度变迁对农业经济增长的贡献很大［5］;李金诚认为农业经济增长方式转变的核心在于提高投入产出比，应努力提高农业科技成果产业化水平［6］;韩作生建立了向量自回归(VAR)模型就农业科技人力资本对农业增长的促进作用进行检验，发现科技人力资本的贡献要超过物质资本的投入［7］。白晓燕分析了我国农业政策性金融对农业增长的作用，并使用最优子集回归验证了两者间的紧密联系［8］。

根据以上研究可以看出当前关于农业产出和增长影响因素分析大多是从线性角度考虑的，分析各类因素对农业产出或增长的作用时缺乏非线性考虑——这正是本文研究的核心内容。同时在农业要素投入产出弹性的测度上，很少有学者考虑到农民收入水平变化对农业要素投入产出弹性的影响，本文认为在相同的要素投入条件下，会因农民收入水平变动导致要素投入产出弹性也发生变动，所以下文将采取Hansen在1999年［9］提出的门槛估计方法使用江苏13个地区2002-2011年的面板数据，对农业物质要素投入与农业产出之间的关系进行非线性分析，以验证农民纯收入变动对农业物质要素投入产出弹性的影响。

二、模型设定与估计方法

(一)模型设定

1.门槛变量选取

已有很多研究证明农民收入变动对农业物质要素投入数量有显著的影响，如李孝忠和乔娟认为农民收入结构对东北地区大豆播种面积波动有显著影响作用［10］;何政道和何瑞银通过对1989-2006年江苏数据进行分析发现:影响农业机械总动力的因素主要是农村剩余劳动力转移率和农村居民家庭人均纯收入［11］;马骥利用2006年华北平原的调研数据进行分析，发现家庭非农收入对化肥施用量有显著影响［12］。上述研究都证实了农民收入变动会引起农业各物质要素投入数量的变动，意味着农民收入间接影响了农业产出，但是目前关于农业要素投入产出弹性测算的文献很少考虑到因农民收入水平差异导致的要素投入产出弹性差异。本文认为:农民收入水平变动不仅通过影响农业生产中物质要素数量这一途径对农业产出产生影响，还会通过以下两个途径对农业产出产生影响:一是农民收入水平变动导致农业要素组合结构发生变更从而改变要素的产出弹性，收入增加促使了农户加大资本性生产投入支出，如提高农机购置和土地承包的数量，二是农民收入提高在使农民形成现代市场经济观念的同时也让农民有更多的资本去主动寻求各类技术培训和学习，让农民的生产技能得到较大的提高，特别是在大力推广农业机械化过程中农民操作、维护技术的提升。所以在进行农业物质要素投入产出弹性测算时，应当考虑到农民收入的影响。借鉴黄凌云等人［13］的做法，将农民纯收入作为门槛变量，构建以下模型:

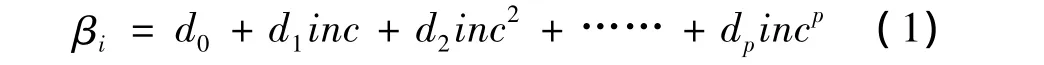
式(1)表示以农业生产函数中第i个要素的弹性系数βi为被解释变量、农民收入inc的多次项inc，inc2，……，incp为解释变量的回归方程中，如果dp(p≥2)显著不为0，说明可以将农民收入分成p个区间，在每个区间中农民收入与βi的关系是不同的，上述表述是刻画“门槛效应”的“交叉项模型法”，但黄凌云等人认为交叉项模型法虽然可以估计出具体门槛值，但无法验证所估计门槛值的正确性，也无法对内生“门槛效应”进行显著性验证，采用面板门槛估计能够较好的弥补这个缺陷［14］。

2.门槛模型建立

经典的柯布－道格拉斯生产函数为:

(2)中Y代表农业产出，A代表一定时期内恒定不变的技术水平，K和L为投入的资本要素和劳动力，α和β分别为资本和劳动力的产出弹性，α+β＞1(＜1，=1)表示规模报酬递增(递减，不变)。两边求导得到:

借鉴党超的定义［4］:农业机械总动力、农业用电量、化肥施用量可以衡量资本的影响，而农作物播种面积、有效灌溉面积可以衡量土地的影响。结合劳动力要素，构建生产函数为:

对两边求导后得到:

其中Y表示农业产出，L表示农业劳动力数量，s表示农作物播种面积，mech表示农业机械总动力，ch表示化肥施用量，elec表示农业用电量，gg表示有效灌溉面积。变量取对数处理，以消除异方差影响。β1，β2，β3，β4，β5，β6表示待估计参数，μ 为不可观测的个体效应，ε为随机扰动项。

式(5)是线性方程，没有考虑到变量关系的结构性变更。为了考察变量关系具有的非线性门槛效应，将农民纯收入(inc)作为门槛变量，在核心变量和控制变量的确定上，因为农业劳动力过剩导致的产出弹性为负是一个不争的现实，发展生态农业的大背景下减少化肥施用量、实现农业可持续发展已是大势所趋，所以本文不考察这两个变量的门槛效应。农民收入提高直接提升了对农业机械的需求量，促使农民在地方政府采取“民办公助”的方式增加对农民用水户协会管理的田间工程投入的政策背景下更加积极的参与灌溉管理、提高灌排工程设施基础能力，也促使农民扩大播种面积和增加了农业生产中的用电量。基于以上考虑，本文将lnL，lnch作为控制变量，分别将 lnmech，lngg，lns，lnelec 作为核心变量，形成4个单门槛效应估计方程:

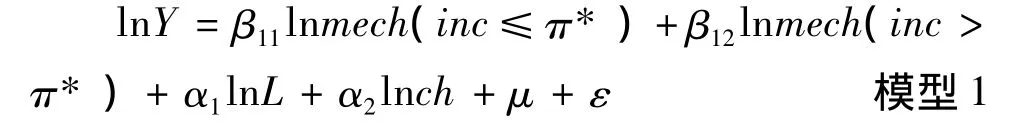
其中，π* 是门槛变量inc的门槛值，βij(i=1，2，3，4;j=1，2)表示对应第i个核心变量在第j个门槛状态下的待估计参数，α1，α2为控制变量待估计参数。对于多门槛效应，可以进一步按照门槛区间设定要求进行拆分，不再赘述。

(二)估计方法

为了简化起见，只根据模型1进行估计方法描述。设定:

为了去除个体效应μ的影响，需要先进行组内均值处理，然后将所有数据叠加，从而有以下方程:

在门槛变量(inc)区间中任意选取选取一个门槛值π1替代π*代入模型(6)进行OLS估计，记录下残差平方和SSE(π1)，再选取另外一个门槛值π2，估计后得到 SSE(π2)，根据残差平方和最小化原则确定较优门槛值，再选取其他门槛值进行估计后得到残差平方和与前者进行比较，在多次迭代计算后确定最优门槛值π*=argminSSE(inc)。黄凌云等认为:实际计算过程中采取逐步法实现的计算量过大，采用格栅法(Grid Search)能够加快计算速度。

Hansen最大的贡献是提出了对门槛效应个数和门槛值显著性的“自抽样”(Bootstrap)检验过程，这克服了以往门槛判定过程中使用分组检验法和交叉模型法不能对门槛显著性进行检验的缺陷，他提出了一个F统计量:

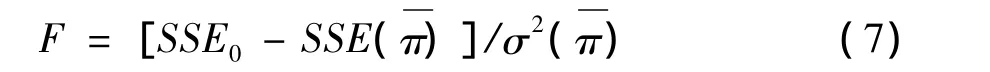
SSE0表示在不存在门槛效应原假设(所有核心变量估计参数满足:βi1=βi2，∀i)条件下进行OLS估计得到的残差平方和，SSE)和 σ2()为存在门槛效应下进行估计后得到的残差平方和与残差方差。因为门槛值事先未确定，可以使用“自抽样”(Bootstrap)模拟F值的渐进分布。对于估计出的门槛值，需要检验其真实性，有:

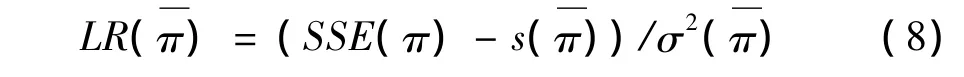
Hansen认为当LR(π)＞－2ln(1－(1－α)0.5)时可以拒绝门槛值不真实的原假设，α为相应水平。在确定了第一个门槛值后，可以再在门槛变量区间中任意选取一个值作为第二个门槛值的初始值，同样利用残差平方和最小准则根据上述步骤确定门槛值，并对第二个门槛值的显著性与真实性进行检验，如果检验出第二个门槛值也显著并真实，可以再用上述过程判定是否存在其他的门槛值，过程如上所述，在此不再赘述。

三、数据样本与变量描述

本文采用2002-2011年江苏13个地区(南京、无锡、徐州、常州、苏州、南通、连云港、淮安、盐城、扬州、镇江、泰州、宿迁)的面板数据进行实证分析。农业产出采用农林牧副渔业总产值进行衡量，为了剔除价格变动带来的影响，采用江苏各年第一产业生产总值指数对其进行调整。要素投入指标包括农林牧副渔从业人员数量、农作物播种面积、农业机械总动力、化肥施用量、农业用电量、有效灌溉面积等6个指标。门槛变量为农村居民人均纯收入。数据来源于各年《江苏统计年鉴》，具体变量说明及描述性统计结果如表1所示。

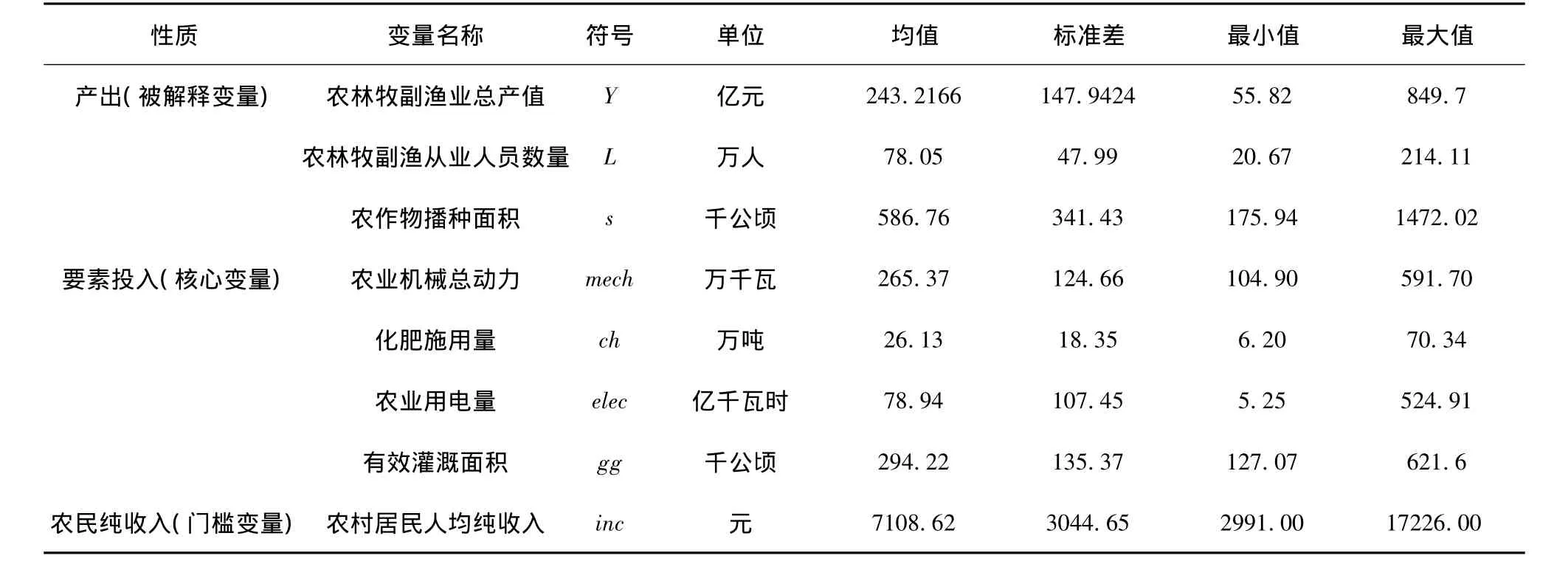
表1 变量说明及描述性统计(2002-2011年，N=13地区，T=10年，NT=130)

图2-1至2-6是描述lnY序列与各个解释变量对数序列间关系的的散点图，有以下结论:①劳动力数量对数与与农业产出对数间的关系在江苏绝大部分地区均表现明显的负相关。②播种面积对数与农业产出对数之间的关系在江苏各个地区有显著差异，无锡、常州、镇江等地区整体上表现为播种面积对数与农业产出对数无显著关系(散点图路径近似垂直于横轴)，而在扬州、盐城、徐州等一些地区则表现为较为明显的正相关关系，南京、苏州则体现为较明显的负相关关系。③农业机械总动力对数与农业产出对数的关系在各地区存在差异，在包括南通、徐州、盐城、淮安在内的大部分地区体现为正相关，而在无锡、苏州等地区表现为弱负相关。④化肥施用量对数与农业产出对数的关系在苏锡常地区和南京表现为负相关，而在镇江、徐州、盐城等大部分地区则表现为正相关。⑤用电量对数与农业产出对数的关系在各地区体现为正相关关系，但在相关程度上各地区存在一定差异。⑥有效灌溉面积对数与农业产出对数之间的关系在各地区存在差异，从整体上看呈明显正相关关系。

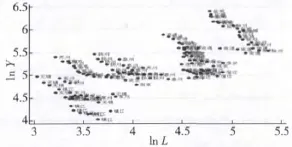
图2 －1 lnL与lnY散点图

图2 －2 lns与lnY散点图

图2 －3 lnmech与lnY散点图 l

图2 －4 lnch与lnY散点图

图2 －5 lnelec与lnY散点图

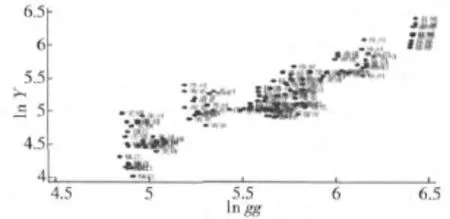
图2 －6 lngg与lnY散点图

四、实证分析

(一)门槛效应检验

根据上文模型设置，利用Stata 11.0软件进行计算。因为需要考察的核心变量个数不唯一，如果分别进行门槛效应检验可能会使模型1—模型4产生不同的门槛区间个数，不利于从总体上考察农民收入变动如何影响了各农业物质要素投入产出弹性，也不利于对比分析，故本文对4个模型均设置为单门槛并进行检验和估计。表2是给出了单门槛效应的检验结果，第2-5列显示4个模型均在1%水平上显著存在门槛效应，最后两列给出了门槛变量的门槛估计值及在95%显著性水平下的置信区间。图3-1至3-4是四个门槛模型估计得出的门槛检验图，横轴为门槛变量，纵轴为LR值，图中标明了95%显著性参考线，当曲线处于参考线下方意味着此部分门槛值显著存在。从估计结果看，四个模型中有三个模型的门槛估计值相同，说明当农民人均纯收入处于10600元门槛值两边时，农业机械总动力、灌溉面积、农业用电量对农业产出的弹性存在显著差异，这体现了以农民纯收入作为门槛变量考察农业物质要素投入与产出间的非线性关系时门槛模型具有较强的一致性。

(二)估计结果

表3显示了4个模型的单门槛效应稳健标准差估计(Robust)结果，有以下结论:①模型1、2、3均认为农业劳动力数量对农业产出的弹性系数在1%水平显著为负，说明江苏各地区整体上仍然存在着农村劳动力过剩的状况，但模型4认为农业劳动力产出弹性在5%水平显著为正。化肥施用量对农业产出的弹性在四个方程中不一致，模型1和模型4的估计结果认为在10%检验水平上化肥施用量的产出弹性不显著，模型2估计结果显示化肥施用量产出弹性在1%检验水平下显著为正，模型3估计结果显示在5%水平下化肥施用量产出弹性显著为负。②核心变量估计结果显示:在农民纯收入低于等于10600元时，农业机械总动力水平每提高1%，农业产出将增加0.53%，而农民纯收入跨越10600元这个门槛时，农业机械总动力水平每提高1%，农业产出将增加0.57%，说明农民纯收入的提高有助于提升农机动力单位投入产出弹性;在农民纯收入低于等于10600元时，有效灌溉面积每提高1%，农业产出将增加0.69%，而农民纯收入跨越这个门槛值后，有效灌溉面积每提高1%，农业产出将增加0.73%，说明农民收入提高后会有更多的资本注入农田灌溉领域，更有利于节水工程的推进和灌溉效率的提高，从而使单位灌溉面积增加引起的产出增加;在农民纯收入低于等于10600元时，农业用电量每提高1%，农业产出将增加0.35%，当农民纯收入跨越该门槛时，产出弹性增加到0.3853，农民收入提高直接加快了农村电气化改造进程，也使农村居民节能电器使用率得到提高，从而使单位用电量的产出效应更大。相比于农业机械总动力、有效灌溉面积、农业用电量，播种面积与农业产出间非线性关系的拐点对农民纯收入的要求相对较高，门槛值为11800元，当农民纯收入低于该门槛值时，播种面积每增加1%，农业产出将增加1.72%，当跨越该门槛值时，播种面积每增加1%，农业产出将增加1.75%。上述分析结果验证了本文观点的正确性，农民纯收入的提高对农业物质要素投入产出弹性产生了实质性的影响，当农民纯收入跨越既定门槛值后，农机总动力、有效灌溉面积、农作物播种面积、农业用电量的产出弹性都有所增加。

表2 1000次“自抽样”(Bootstrap)的门槛效应检验结果

图3-1 模型1门槛检验图

图3-2 模型2门槛检验图

图3-3 模型3门槛检验图

图3-4 模型4门槛检验图

(三)各地市门槛状态判定

根据两个门槛值(10600和11800)，将江苏13个城市进行分类。从表4可以看出2011年南京、无锡、常州、苏州、南通、扬州、镇江、泰州等8个地区的农民纯收入已经跨越10600元处于较高农民纯收入区间，而徐州、连云港、淮安、盐城、宿迁等5个地区农民纯收入未跨越该门槛，但盐城农民纯收入已经为10511元，即将跨越门槛值进入较高区间。南京、无锡、常州、苏州、镇江等沿江5市农民纯收入同时超过11800元，而其他8个地区均处于该门槛值以下。通过以上分析，认为苏锡常、南京、镇江等地区的农作物播种面积的产出弹性与其他未跨越相应门槛值的地区存在一定差异，苏中地区(南通、扬州、泰州)农机化动力、有效灌溉面积、农业用电量等要素的产出弹性与苏北地区(徐州、连云港、淮安、盐城、宿迁)等地区存在着显著差异。

表3 单门槛模型稳健标准差估计结果

表4 2011年江苏各地区门槛状态划分

五、全文总结

本文利用2002-2011年江苏13个地区的面板数据，构建了以农民纯收入为门槛变量的农业物质要素投入与农业产出的门槛模型，主要结论如下:

一是农业机械总动力、有效灌溉面积、农作物播种面积、农业用电量等土地、资本要素与农业产出间的关系存在着非线性特征。当农民纯收入高于10600元时农机总动力，有效灌溉面积、农业用电量带来的产出弹性分别为 0.5723、0.7344、0.3853，高于未跨越10600元门槛值时的0.5273、0.6900、0.3475，三种要素的投入产出弹性在门槛值左右两侧的差异分别为 0.045、0.0444、0.0378，说明农民纯收入超过10600元门槛值时，按照产出弹性增加量的要素排序为:农机总动力＞有效灌溉面积＞农业用电量。当农民纯收入高于11800元时，播种面积带来的产出弹性也有所增加，从1.7151增加到了1.7466，计量分析结果充分证明了农民纯收入提高会对各农业生产物质要素的投入产出弹性形成显著影响。

二是2011年江苏13个地市平均农民可支配收入为11834.77元，跨越了11800元的门槛值，意味着江苏农业生产各物质要素与农业产出的关系已经进入了一个新的阶段，所以江苏应当在实现农民增收的同时，大力推广农业科技和农业机械化以实现单产效率的提高，同时土地作为农业生产的基本要素，一定要保证播种面积数量维持在一个合理的水平，并且要努力实现播种面积的稳中有升和不断提高土地产出率。因为农村用电量的产出弹性有所提高，国家电力部门应当积极主动与农业部门和各级乡镇建立连接机制，对区域农业生产用电需求进行预测并合理配置电力负荷，积极进行供电创新、优先满足农业生产用电需求。

三是江苏整体上农业生产中化肥施用量产出弹性不明确，但从散点图来看，在一些苏北地区化肥施用量与农业产出为正相关关系，这些地区在一定时期内化肥施用量还会有所增加，农业部门应当掌握化肥投入面源污染的变化规律及其驱动机制，并引导农民采用亲环境的施肥技术、降低农户化肥施用水平。

四是苏南和苏中地区的农民纯收入水平较高，有效的提升了农业物质要素投入产出弹性，但宿迁、淮安、连云港等地区的农民纯收入仍在9000元门槛值以下，距离10600元门槛值还有一定的距离，制约了农业物质要素投入产出弹性的提高，所以应当采取各种有效手段促使苏北地区农民纯收入得到较快增长。

［1］江苏省粮食首次实现九连增，总产量保持全国第四.http://www.js.xinhuanet.com/2012-12/07/c-113938129.htm［EB/OL］，2012-12-07

［2］吴玉鸣.中国区域农业生产要素的投入产出弹性测算——基于空间计量经济模型的实证［J］.中国农村经济，2010(6):25-37，48

［3］林玉芯.农业投入产出生产函数及其应用研究［J］.数学的实践与认识，2007(13):102-108

［4］党超.物质要素投入对我国农业产出水平的影响——基于省际面板数据的实证分析［J］.宁夏大学学报(人文社会科学版)，2011(6):109-116

［5］乔榛，焦方义，李楠.中国农村经济制度变迁与农业增长——对1978-2004年中国农业增长的实证分析［J］.经济研究，2006(7):73-82

［6］李金诚.农业科技成果产业化与农业经济增长方式的转变［J］.农业经济问题，1998(9):53-55

［7］韩作生.农业科技人力资本对农业经济增长影响的实证分析——以山东省为例［J］.山东大学学报(哲学社会科学版)，2011(4):86-92

［8］白晓燕，李锋.我国农业政策性金融对农业经济增长贡献的实证研究［J］.农业经济问题，2005(7):21-24

［9］ Hansen B E.Threshold effects in non-dynamic panels:Estimation，testing and inference［J］.Journal of econometrics，1999，93(2):345-348

［10］李孝忠，乔娟.东北地区大豆播种面积波动及原因分析［J］.新疆农垦经济，2009(4):6-12