SMA预拉杆式自定心屈曲约束支撑的滞回性能分析
2014-06-28孟少平王维影
谢 钦 周 臻 孟少平 王维影
(东南大学混凝土及预应力混凝土结构教育部重点实验室,南京210096)
屈曲约束支撑(BRB)是一种用于抵抗地震作 用的支撑构件,它由承受轴向荷载的核心单元和防止核心单元产生低阶屈曲的约束单元组成.地震时,借助BRB核心单元的屈服耗能可控制结构的地震响应[1].BRB 性能稳定,减震效果显著,受到广泛关注[2-5].
研究表明,BRB屈服后的刚度较低,使得主体结构在强震后会产生较大的残余变形[6],增加了结构的维修成本.将后张预应力技术引入BRB,形成自定心约束支撑(SC-BRB),能有效解决该问题.Christopoulos等[7]通过将内外套筒与预张拉芳纶纤维筋组合,形成自定心系统,并引入到摩擦耗能支撑体系中.在此基础上,Chou等[8]提出了一种双核摩擦耗能支撑体系,通过串联2组预拉杆,使得自定心系统的变形能力扩大了2倍,降低对预拉杆最大弹性应变的要求.Miller[9]将具有超弹性的形状记忆合金(SMA)作为预拉杆引入SC-BRB中,并通过试验证实了这种支撑具有良好的自定心效果和变形能力.
由于SMA具有非线性的本构关系,且其材料性能受环境温度影响,因此本构模型的建立比较困难.BRB的受力性能也较为复杂,经试验证实,其滞回曲线具有拉压响应不对称和等向强化特性.对于采用SMA作为预拉杆的SC-BRB(简称SMASC-BRB),目前尚无可简便有效描述其滞回性能的弹塑性模型.流变模型是一种用于描述材料循环非线性行为的理论方法,经证实其能有效模拟BRB 的滞回曲线[10].
本文通过将SMA的分段线性本构模型与流变模型结合,建立了一种用于研究SMA-SC-BRB滞回性能的流变分析方法,并利用该方法讨论了几个重要参数对SMA-SC-BRB滞回性能的影响.
1 SMA-SC-BRB的构造
SMA-SC-BRB的构造如图1所示[9].核心板放置于内套管中并灌注砂浆,以避免其在受压时出现平面外屈曲.自定心体系由中套管、外套管和预拉杆组成.为了充分利用SMA的超弹性特征,将SMA杆和普通钢杆串联形成预拉杆.将中套管的左端和外套管的右端分别与核心板侧边焊接,而另一端均保持自由状态,端板在预拉力的作用下紧贴套管两侧.当支撑受拉时,端板在中套管和外套管焊接端的推动下向两侧移动,并与自由端分离;当支撑受压时,端板又在中套管和外套管自由端的推动下向两侧移动,并与焊接端分离.由此保证支撑无论处于受拉或是受压状态,预拉杆始终受拉伸长,为支撑持续提供自定心所需的恢复力.
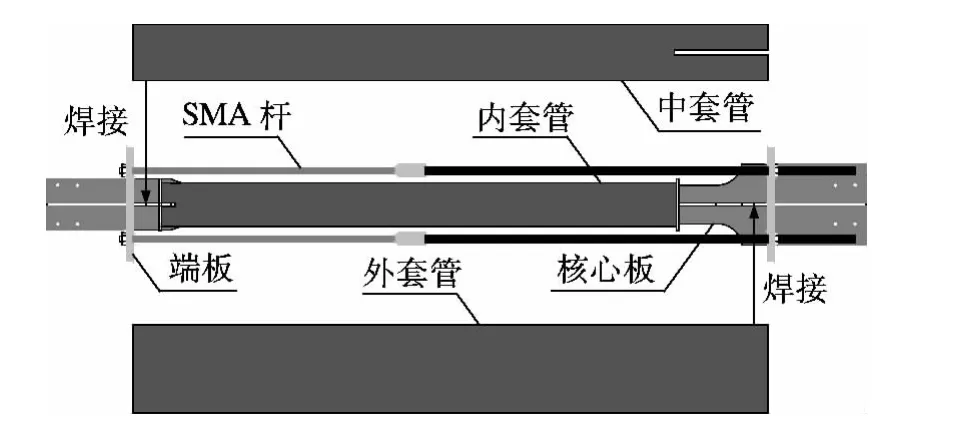
图1 SMA-SC-BRB的设计构造[9]
图2为SMA-SC-BRB的理论滞回曲线.图中,FP为初始预张力,dys为FP作用下套管产生的压缩变形量.当外荷载小于FP时,端板与套管端部并未分离,自定心体系的刚度为预拉杆、中套管和外套管的刚度之和;当外荷载大于FP时,端板与套管的一侧脱开,此时自定心体系的刚度为预拉杆刚度.从图中可以看出,SMA-SC-BRB的滞回曲线具有明显的旗帜形特征,其残余变形远小于BRB,自定心效果比较显著.
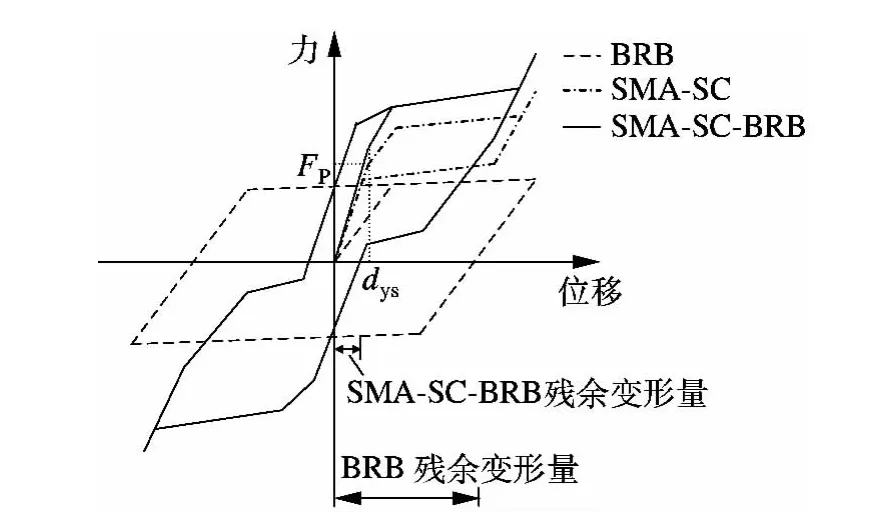
图2 SMA-SC-BRB的理论滞回曲线
2 SMA的本构模型
Brinson[11]以热力学基本定律为基础,建立了SMA的一维本构模型.其本构方程为
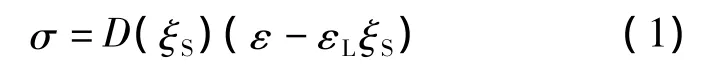
式中,σ,ε分别为SMA的应力和应变;εL为最大残余应变;ξS为由应力引发的马氏体含量;D(ξS)为SMA的弹性模量,计算公式如下:
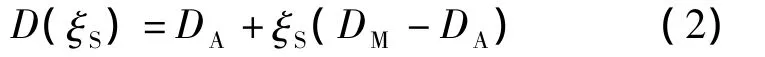
式中,DM,DA分别为SMA的马氏体弹性模量和奥氏体弹性模量.
由于Brinson提出的本构模型应力与应变为非线性关系,为保证计算结果的收敛,对位移步的选取有严格的要求.为简化分析过程,将SMA的相变曲线段简化为直线,建立SMA分段线性本构模型[12](见图3).图3中各直线段根据其斜率特点可归为2类:① 非相变直线段,如P1P2,P4P5,P6P7和P8P9,其弹性模量可根据各直线段的起始点应力值由式(2)计算得出.②相变直线段,如P2P3,P5P6,P7P8和P9P10,其弹性模量由起始点的应力应变值与马氏体相变结束点(P3)或奥氏体相变结束点(P1)的应力应变值决定.P1,P2,P3和 P5为SMA本构模型的4个关键点.结合各段的弹性模量Di和起始点的应力值σi0,可得到SMA的应力应变关系为
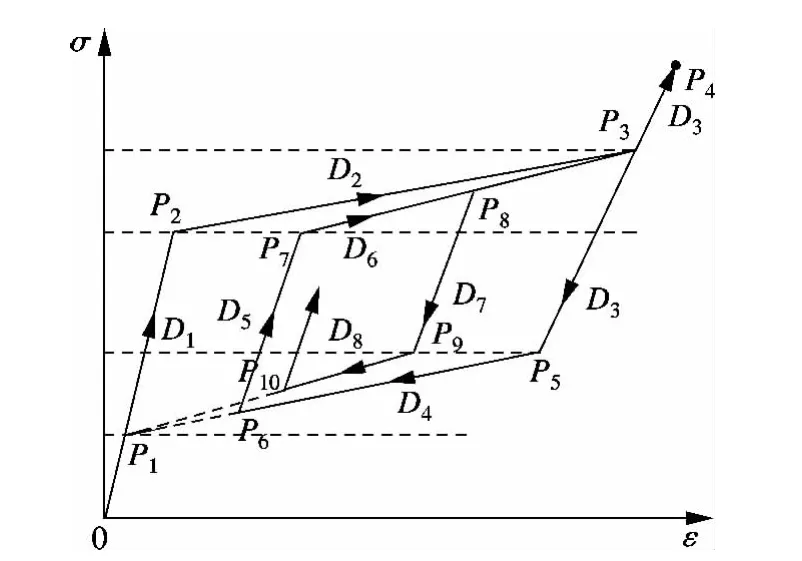
图3 SMA的分段线性本构模型
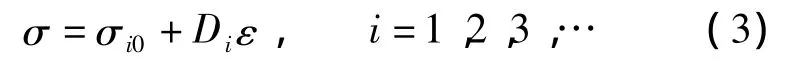
3 SMA-SC-BRB的流变模型
3.1 模型描述
SMA-SC-BRB的滞回性能可视为由2个部分并联组成:通过材料屈服耗能的BRB部分和提供自定心力的SMA-SC部分.文献[10]通过将流变元件与弹簧1并联再与弹簧0串联来模拟BRB.在此基础上,本文再并联了弹簧SMA-SC(见图4),以实现对SMA-SC-BRB旗帜形滞回曲线的模拟.图中,d0和d1分别为BRB的弹性位移和塑性位移;dSC为SMA-SC的位移;F0,F1和 FSC分别为由对应位移d0,d1和dSC所引起的力,且FSC为自定心系统的恢复力;k0和k1分别为BRB的弹性刚度和屈服后刚度;kSC为SMA-SC的刚度,包含端板与套管分离前、后SMA-SC的刚度kSC1和kSC2.需注意的是,该模型不能对BRB强度退化后的力学性能进行模拟.
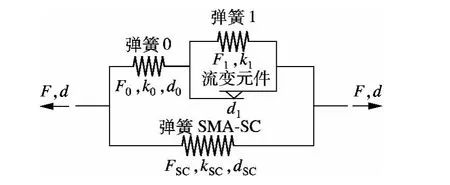
图4 SMA-SC-BRB的流变模型
3.2 控制方程
求解支撑滞回性能时,通常采用位移加载制度,结合模型各部件力与位移的控制方程,建立支撑总力F与总位移d的关系.计算时,力与位移均以支撑受拉为正,受压为负.
由图4可知,支撑总位移d可由BRB的弹性位移d0与塑性位移d1叠加得到,即
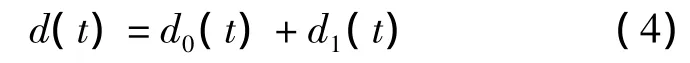
SMA-SC系统的位移则与支撑总位移d相等,即

支撑力F可分解为
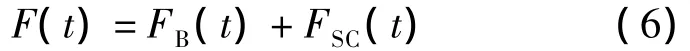
式中,FB为BRB承受的力.根据加载位移d(t),先分别求解出t时刻的FB(t)和FSC(t),然后求和得到支撑总力F(t).
3.2.1 FB的计算
由于FB与弹簧0所承受的力相同,因此FB的增量可表示为
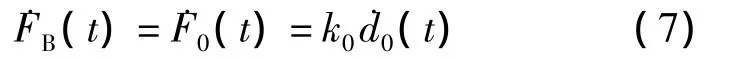
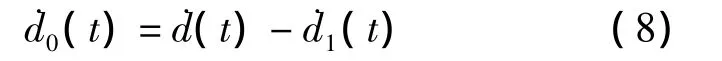
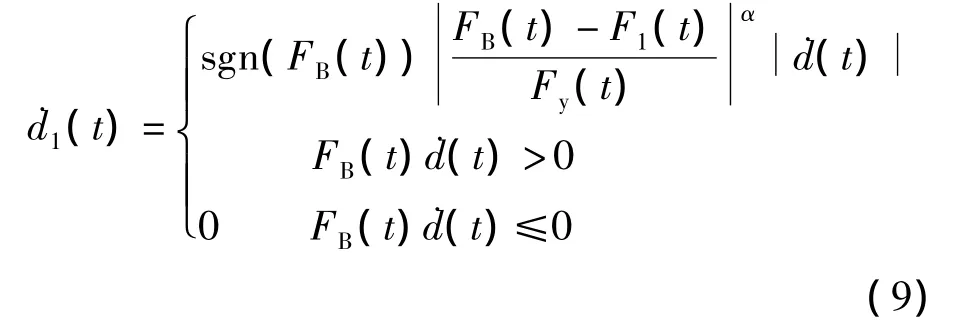
式中,α为基于试验结果的实常数,用于控制BRB的弹、塑性变形转换梯度,α值越大,转换梯度也越大;F1(t)为弹簧1承受的力,且

Fy(t)为BRB强化后的屈服强度,且
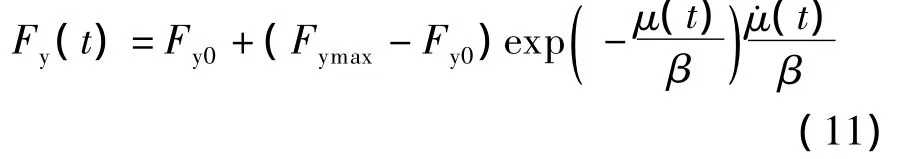
式中,Fy0为BRB的初始屈服强度;Fymax为BRB等向强化极限状态的屈服强度为BRB塑性位移增量的绝对值;μ(t)为累计塑性位移,即μ(t)=为基于试验结果的实常数,用于控制BRB的等向强化速率,β越大,等向强化速率越慢.为精确模拟BRB的拉压响应不对称性,BRB受拉和受压时式(9)和(11)中的α,β和Fymax可分别取不同值.
3.2.2 FSC的计算
由于预拉杆是由SMA杆和普通钢杆串联组成的,因此当预拉杆伸长˙d(t)时,SMA杆的伸长量和应变增量分别为
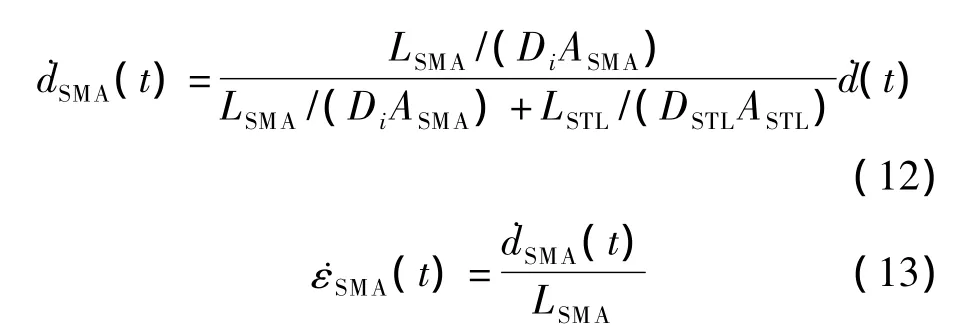
式中,LSMA和ASMA分别为SMA杆的长度与截面面积;DSTL,LSTL和ASTL分别为钢杆的弹性模量、长度与截面面积.将εSMA代入式(3)便能计算出SMA杆的应力σSMA.
预拉杆的初始预张拉力FP会使套管受压并产生压缩变形dys,且

结合自定心体系的工作原理,通过判断支撑位移d(t)是否大于dys,可将FSC的计算分为以下2种情况:
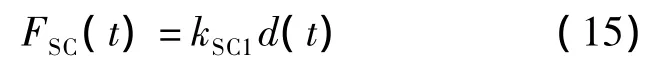
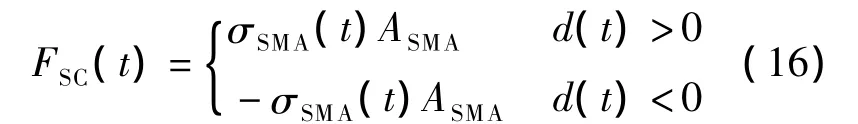
结合材料试验和支撑的部件尺寸,确定建立流变模型的重要参数.根据拟采用的位移加载制度,将加载过程分为n个时间段,并确定每个时间点的位移d(t).利用数值分析软件Matlab根据式(7)~(11)以及式(12)~(16)计算出 FB(t)与FSC(t),并求和得到t时刻的支撑总力F(t),然后进入下一时刻继续计算.当求出n个时间点的支撑总力F后,即完成整个分析过程.
4 与试验结果的比较
利用SMA的分段线性本构模型与SMA-SCBRB流变模型对文献[9]中的试验进行数值模拟,并与试验结果进行对比,以验证本文模型的正确性.
4.1 SMA分段线性本构模型的验证
根据文献[9]中SMA的材料参数,由分段线性本构模型绘制出SMA的应力应变曲线,并与试验值进行对比(见图5).从图中可以看出,采用分段线性模型能较好地适应SMA的非线性本构关系,尤其是在奥氏体阶段和马氏体阶段,模拟值与试验值十分接近.在奥氏体相变和马氏体相变的过程中,当马氏体含量ξ较小时,分段线性模型的模拟值与试验值吻合较好,而随着马氏体含量ξ的增大,误差也逐渐增大.造成误差的原因是:SMA的相变是一个非线性过程,而SMA分段线性模型的相变段是一条直线,因此不可避免会产生误差.总体而言,分段线性本构模型不但能有效简化SMA本构关系的构建,而且模拟结果较为准确.
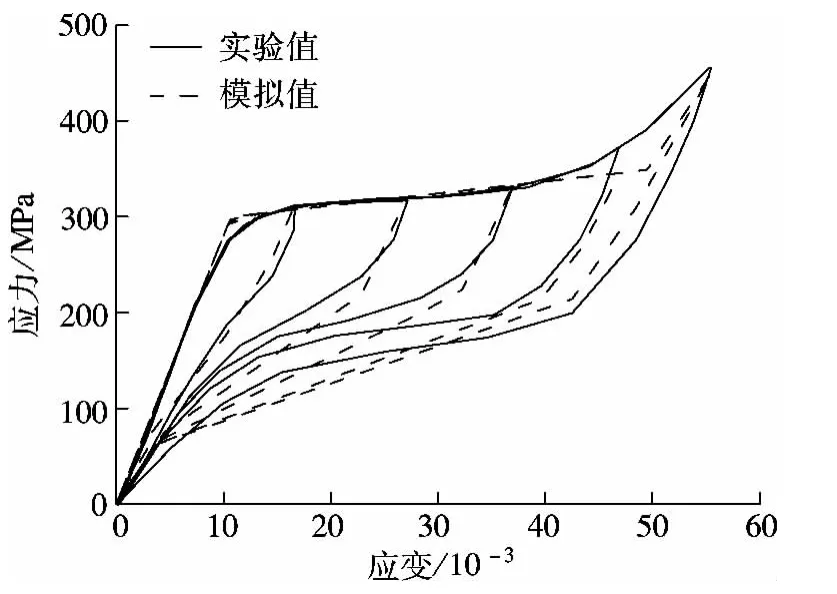
图5 SMA试验值与模拟值的对比
4.2 SMA-SC-BRB流变模型的验证
在文献[9]的SMA-SC-BRB试验中,支撑中各构件的几何尺寸如图6所示.根据SMA-SCBRB的材料试验和各构件的尺寸,确定流变模型的重要参数(见表1).
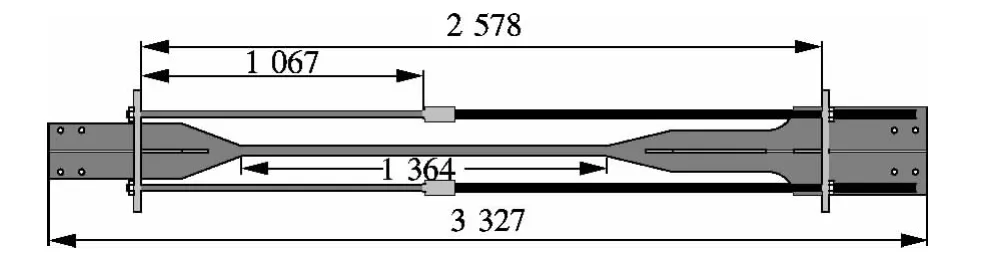
图6 SMA-SC-BRB的几何尺寸[9](单位:mm)

表1 流变模型重要参数
由流变模型得到的模拟值与试验值的对比见图7.从图中可以看出,2组滞回曲线都具有旗帜形特征,但均存在残余变形,说明预拉杆起到了减小残余变形的作用,但还未达到完全自定心.流变模型的模拟值与试验值十分接近,但流变模型在加载阶段的刚度相对于试验结果较大,而其残余变形却相对较小,其原因可归结于支撑的加工误差导致的刚度削弱以及预应力损失等情况的出现.整体而言,采用流变模型对SMA-SC-BRB进行模拟分析具有较高的精确度,能较准确地绘制支撑的滞回曲线.
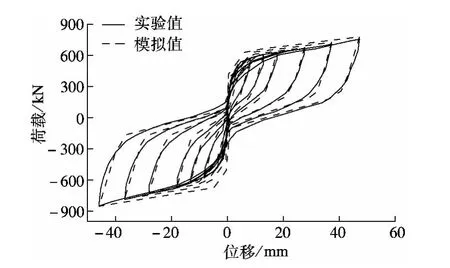
图7 SMA-SC-BRB试验值与模拟值的对比
5 参数分析
对于SC-BRB而言,初始预张力、预拉杆的截面面积和BRB核心板的截面面积是影响支撑耗能能力与自定心特性的3个关键参数,而温度会对SMA杆的力学特性产生影响.本节运用流变模型,通过逐一改变文献[9]中试验构件的4个参数,分析这些参数对SMA-SC-BRB滞回性能的影响.由于中套管和外套管仅作为自定心体系的推杆,对支撑的滞回性能影响较小,因此本文不对其进行讨论.
5.1 初始预张力
分别取初始预张力 FP=130,200,300 kN,以考察FP对SMA-SC-BRB滞回性能的影响.采用流变模型计算得到3组滞回曲线(见图8).
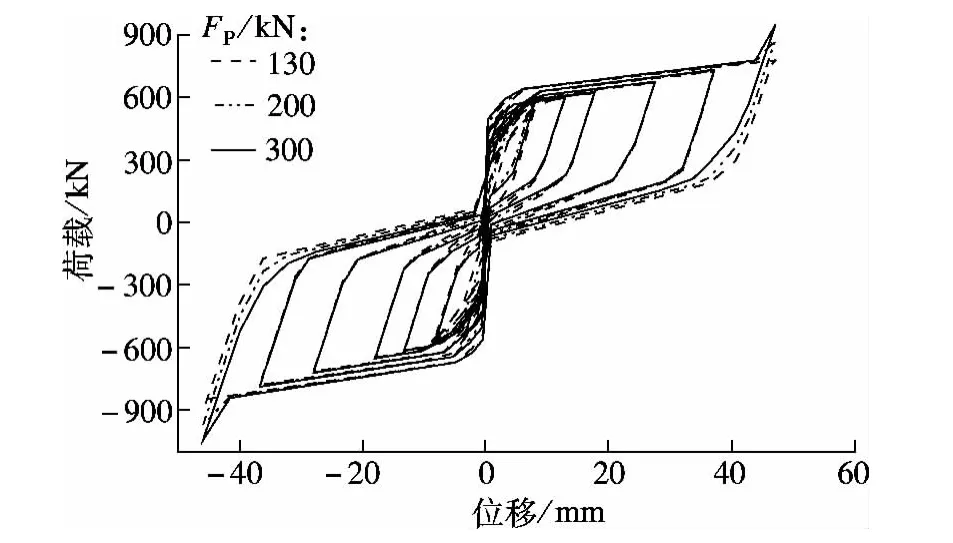
图8 不同初始预张力下SMA-SC-BRB的滞回曲线
通过对比可知,增加初始预张力不能有效改善支撑的自定心能力,其原因在于:对于SMA杆,若初始预张力FP引起的应力大于奥氏体相变的结束应力,将导致在施加预应力时SMA杆处于奥氏体状态,其弹性模量DA较大,而卸载时SMA杆处于奥氏体相变状态,其弹性模量D(ξ)则较小.即使初始预张力提升较多,但在卸载时SMA杆的内力变化却较小,而支撑在循环往复荷载作用下,自定心力是由SMA杆卸载时的内力提供的,故支撑的自定心能力改善不明显.
由此可知,在设计SMA-SC-BRB时,当初始预应力大于奥氏体相变的结束应力时,不应通过继续提高FP来提升支撑的自定心能力.
5.2 SMA杆的截面面积
分别取支撑中SMA预拉杆的总面积ASMA=1 464,2 200,2 800 mm2,建立 3 个分析模型,由流变模型计算得到3组滞回曲线(见图9).
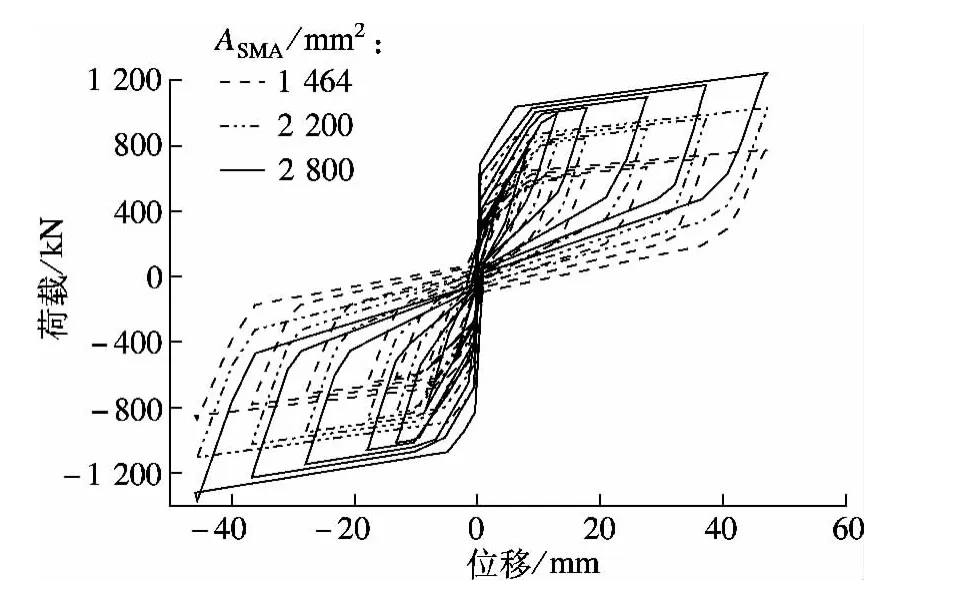
图9 不同SMA杆截面面积下SMA-SC-BRB的滞回曲线
由图9可知,随着SMA杆截面面积的增加,SMA-SC-BRB的自定心能力有了明显的提升.当ASMA=2 800 mm2时,支撑已实现完全自定心.SMA杆自身存在耗能特性,当ASMA增加时,支撑的滞回环面积也随之增大,即耗能能力增强.因此,在考虑经济性的前提下,可通过增加SMA杆的截面面积来提升支撑的自定心能力和耗能能力.
5.3 核心板截面面积
分别取支撑中BRB核心板截面面积ABRB=468,576,684 mm2,由流变模型计算出3 个支撑的滞回曲线(见图10).
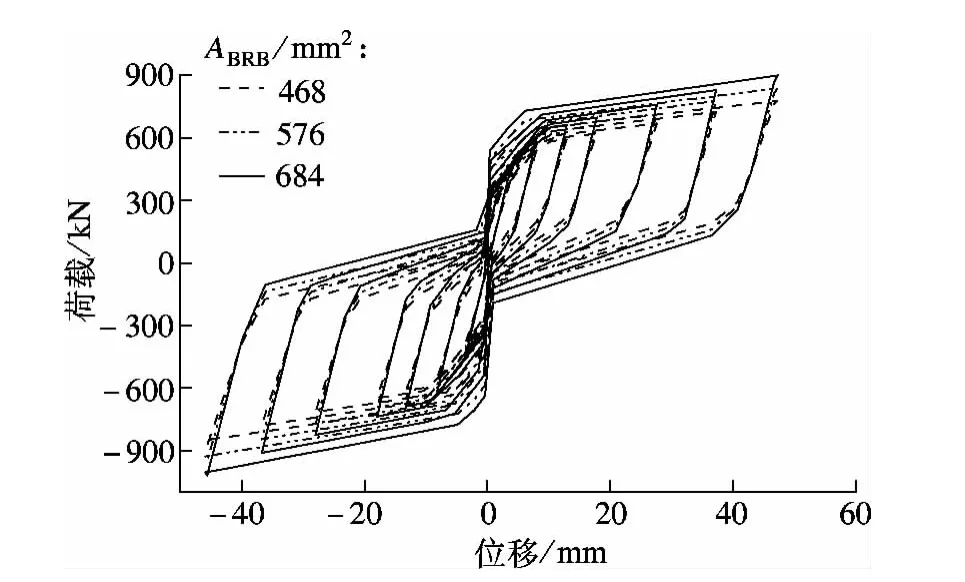
图10 不同核心板截面面积下SMA-SC-BRB的滞回曲线
由图10可知,随着核心板截面面积的增加,SMA-SC-BRB的滞回环也逐渐扩大,耗能能力明显提升.但与此同时,由于ABRB的增加,为克服支撑残余变形所需的力也随之增加,在初始预张力不变的前提下,支撑的自定心能力逐渐减弱.
由此可见,在设计SMA-SC-BRB时,核心板的截面面积应与自定心体系进行协调,在保证支撑自定心能力的前提下,可通过增大核心板截面面积来增加支撑的耗能能力.
5.4 SMA杆的温度
为分析SMA-SC-BRB的滞回性能随温度T的变化趋势,在T=4,6,8℃三种情况下,分别计算并绘制SMA-SC-BRB的滞回曲线,结果见图11.
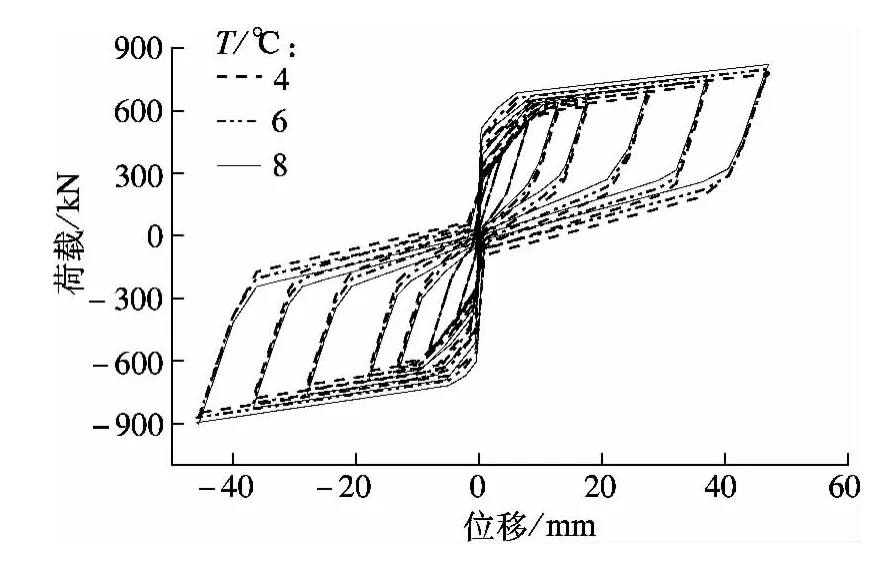
图11 不同温度下SMA-SC-BRB的滞回曲线
由图11可知,伴随着温度T的增加,支撑的自定心能力明显提升.当T=8℃时,支撑的残余变形小,基本实现了完全自定心.造成这种变化的原因在于,温度T的增加会使SMA的形状记忆特性得到增强.由此可见,在SMA-SC-BRB的使用过程中,对SMA杆加强保温措施是十分必要的.
6 结论
1)将SMA分段线性本构模型与流变理论结合,建立了SMA-SC-BRB滞回性能分析模型,其计算过程简便,便于编制程序.
2)与文献试验结果的对比分析表明:采用的SMA分段线性本构模型能够较准确地描述SMA的非线性行为;SMA-SC-BRB的流变分析结果与试验的滞回曲线吻合较好,验证了所提方法的有效性.
3)SMA-SC-BRB参数分析结果表明:增加核心板截面面积,可提升支撑耗能能力,但自定心能力减弱;当初始预应力大于奥氏体相变的结束应力时,继续增加预张力对支撑自定心能力影响较小;增加SMA杆的截面面积,可以同时提升支撑的自定心能力和耗能能力;提高SMA杆的温度T,可显著提升SMA-SC-BRB的自定心能力.
References)
[1]周云.防屈曲耗能支撑结构设计与应用[M].北京:中国建筑工业出版社,2007:1-2.
[2]李国强,胡宝琳,孙飞飞.国产TJI型屈曲约束支撑的研制与试验[J].同济大学学报:自然科学版,2011,39(5):631-636.Li Guoqiang,Hu Baolin,Sun Feifei.Development and experimental study on domestic TJI buckling-restrained brace[J].Journal of Tongji University:Natural Science Editor,2011,39(5):631-636.(in Chinese)
[3]郭彦林,江磊鑫.型钢组合装配式防屈曲支撑性能及设计方法研究[J].建筑结构,2010,40(1):30-37.Guo Yanlin,Jiang Leixin.Behavior and application of buckling-restrained braces assembled with section steels[J].Building Structure,2010,40(1):30-37.(in Chinese)
[4]赵俊贤,吴斌,欧进萍.新型全钢防屈曲支撑的拟静力滞回性能试验[J].土木工程学报,2011,44(4):60-70.Zhao Junxian,Wu Bin,Ou Jinpin.Uniaxial quasi-static cyclic tests on the hysteretic behavior of a novel type of all-steel buckling-restrained brace[J].China Civil Engineering Journal,2011,44(4):60-70.(in Chinese)
[5]吴京,梁仁杰.屈曲约束支撑核心单元的多波屈曲形态研究[J].工程力学,2012,29(8):136-142.Wu Jing,Liang Renjie.Research on the multi-wave buckling process of the core component of the bucklingrestrained brace[J].Engineering Mechanics,2012,29(8):136-142.(in Chinese)
[6]Sabelli R,Mahin S A,Chang C.Seismic demands on steel braced-frame buildings with buckling-restrained braces[J].Engineering Structures,2003,25(5):655-666.
[7]Christopoulos C,Tremblay R,Kim H-J,et al.Selfcentering energy dissipative bracing system for the seismic resistance of structure:development and validation[J].Journal of Structural Engineering,2008,134(1):96-97.
[8]Chou C-C,CHEN Y-C.Steel braced frames with dualcore SCBs and sandwiched BRBs:mechanics,modeling and seismic demands[J]. Engineering Structures,2014,72(1):26-40.
[9]Miller D J.Development and experimental validation of self-centering buckling-restrained braces with shape memory alloy[D].Chicago,IL,USA:University of Illinois at Urbana-Champaign,2011.
[10]Zona A,Dall'Asta A.Elastoplastic model for steel buckling-restrained braces[J].Journal of Constructional Steel Research,2008,68(1):118-125.
[11]Brinson L C.One-dimensional constitutive behavior of shape memory alloys:thermomechanical derivation with non-constant material functions and redefined martensite internal variable.[J].Journal of Intelligent Material Systems and Structures,1993,4(2):229-242.
[12]Du X W,Sun G.Piecewise linear constitutive relation for pseudo-elasticity of shape memory alloy(SMA).[J].Materials Science and Engineering A,2005,393(1/2):332-337.
