基于特性曲线的电站热力系统故障诊断方法

胥建群 孙友源 杨 涛 周克毅 石永锋 司徒有功

(1东南大学能源热转换及其过程测控教育部重点实验室，南京210096)

(2中国电力工程顾问集团华东电力设计院，上海200063)

(3华电电力科学研究院，杭州310030)

(4大唐南京发电厂，南京210059)

在火电厂实际运行中，往往会出现一个设备或几个设备同时发生性能下降的现象，最终引起整个机组热经济性的下降.这种热力系统出现设备性能下降的工况称为故障工况，而把性能下降的设备称为故障部件［1］;与之对应地，把非故障工况称为参考工况.由于热力系统是一个有机的整体，部件之间相互影响，当系统中有一个设备发生故障时，会出现热力参数偏离参考值，这种热力参数的变化会影响其他非故障部件的运行参数，引起诱导故障［1］;当系统中有多个设备同时发生故障时，各诱导故障之间相互叠加，部件之间相互耦合影响，给准确定位性能下降的具体位置带来困难.

为保证电厂运行的安全稳定，国内外学者对此进行了大量的研究，发展了多种诊断方法应用于电厂热力系统或某些设备的故障诊断，并取得了一定的成果.王清照等［2］采用通过热经济学分析得到2个数学判据判别故障发生的部件.王勇等［3］通过建立热力学仿真模型获得故障数据，引入热经济学结构理论诊断模型，完成故障源的定位.Liu等［4］提出了一种智能诊断方法，应用模糊神经网络(FNN)进行局部诊断，采用多源信息融合技术进行全局诊断，该方法可以快速、准确地完成单一故障诊断和不同类型的多个故障诊断的任务.国外学者对基于 分析方法［5］的热经济学结构理论［6］进行了不断改进和应用［7］，Verda 等［8］研究了控制系统的干预对系统额外资源消耗，并率先提出过滤诊断过程中由控制系统引起的影响.近年来，Heo等［9］采用前馈神经网络开发的诊断模型，成功地检测到给水加热器内部泄漏的位置，并且其量化值也在可接受的误差范围内.Ajami等［10］提出利用独立分量分析(ICA)的方法对汽轮机进行故障检测和诊断，此方法可正确有效地进行故障检测和诊断，避免误报和误诊.

分离和量化诱导故障，实现各部件之间的解耦是进行热力系统故障诊断的关键.为此本文提出了基于热力参数-性能指标特性曲线的诊断模型，并引入不可逆损失［6］作为性能指标，定量计算其在故障工况下相比于参考工况的实际变化量，用以判别故障的部件.以某电厂330 MW机组为例，通过模拟3种故障工况初步证明了该方法的可行性.

1 模型的建立

1.1 基本思想

在火电厂热力系统中，每一个部件都有相应的指标来评价其运行性能，而这一指标又与该部件的热力参数存在一定的函数关系.因此，可以认为系统内每个部件都存在着热力参数-性能指标特性曲线，该曲线表示存在一系列关系式f使得部件的性能指标κ是一组热力参数τ的函数，即

对于任一部件，均可通过假设得到参考工况和故障工况下某一热力参数对应性能指标的特性曲线，其函数关系分别为fref和fmal，如图1所示.工况一旦确定，这种函数关系就随之确定，因此可以认为在系统边界条件一定的情况下，参考工况的特性曲线是不变的，只有当部件发生故障时才会引起特性曲线的变化.

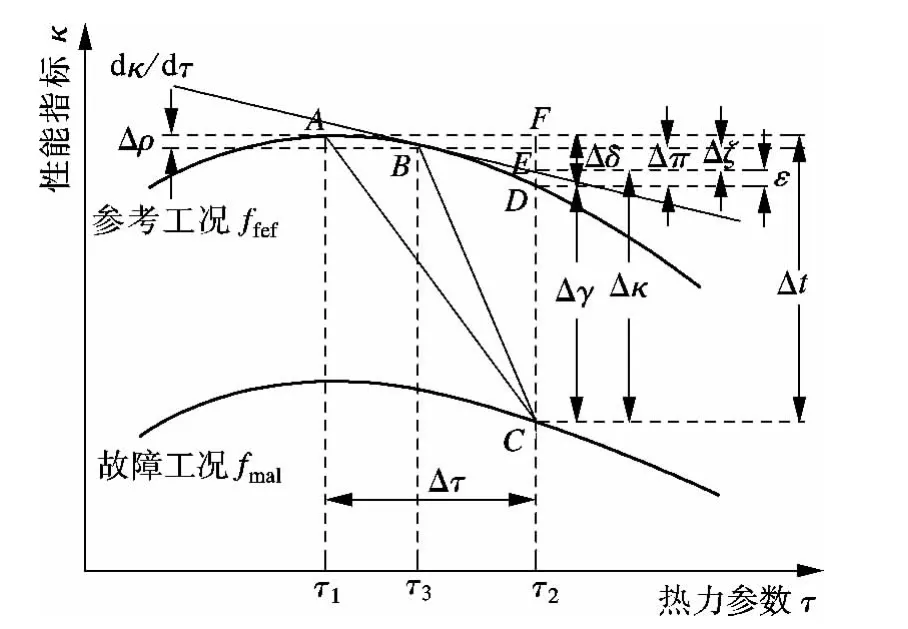
图1 热力参数-性能指标特性曲线示意图

在维持与参考工况相同的轴功功率的前提下，故障工况的各部件会发生热力参数的改变.如图1所示，若某部件存在故障，则当其热力参数从τ1变化到τ2，部件的运行性能点将从参考状态A点变动到一个新的状态C点.2个状态之间的差值表示了该部件运行性能的变化Δι，同时也表示了故障的量化，即

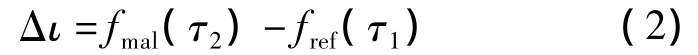
若该部件不存在故障，只考虑参考工况特性曲线，则当热力参数产生Δτ变化时，部件的运行性能点将从状态A点变动到状态D点，表示该部件在无故障工况下亦会产生性能指标的变化Δδ，即

实际上，状态A点变动到C点的过程可以分解为先从A点到D点，再到C点的过程.因此，故障工况下部件的实际故障Δγ(CD段)应为总的性能变化Δι(CF段)扣除无故障时部件仅随热力参数变化就会产生的性能指标变化Δδ(DF段)，即

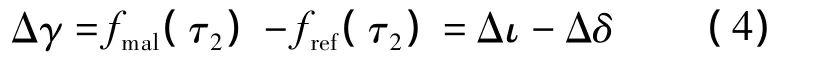
显然地，Δγ只代表了由于部件自身故障引起的性能变化，从理论上消除了其他部件对其产生的影响(即诱导故障)，实现了各部件之间相互影响的解耦.

1.2 消除阀门开度对性能指标影响

由于机组在实际中通常是并网运行，往往要求其输出功率达到一定值.因此在一个恒定功率的条件下讨论所建模型比恒定流量更具实际意义.

在保持功率恒定的故障工况下，流量会增加;调节系统动作，阀门开度的变化会对系统性能指标造成额外的影响，干扰诊断源的准确辨识.一些学者提出了消除由调节系统引起影响的方法［8，11］，基本思想是假想一个同时具有参考工况的阀门开度和故障工况的故障部件工况.本文借鉴其思想提出一个新的假想工况点，并将其与故障工况比较，消除阀门的影响.

假设已得到任一部件在参考工况和故障工况下的功率-性能指标特性曲线，如图2所示.图中状态A点、B点和C点与图1相对应，AC和AC'分别表示定功率和定流量条件下，部件发生故障时性能指标的变化过程;C'点即为文献［8，11］中的假想状态点.而本文假想一个与定功率故障工况阀门开度相同的无故障工况点，定义为自由工况，即图2中的B点.该状态点相比于参考状态A点增加了功率ΔW，并造成了该部件性能指标的变化Δρ;在图1中表示为热力参数由τ1变化到τ3的过程.这一变化量是单纯由于阀门开度的变化而产生的，综合分析图1和图2，Δρ可表示为

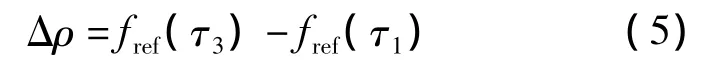
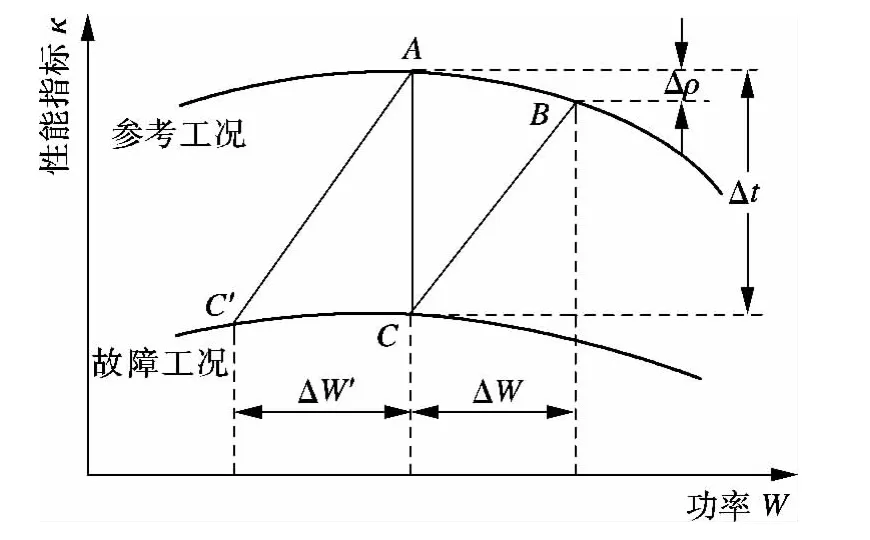
图2 阀门开度对性能指标影响示意图

因此，定功率时故障工况产生的运行性能变化量Δι扣除Δρ即为过滤了调节系统影响的性能指标变化量，在图中表示为BC段.

1.3 性能指标实际变化量的定性分析

根据前文分析，为消除调节系统动作的额外影响，以状态B点代替A点作为参考基准.为此，将图1中Δδ扣除A，B两个基准点性能指标之差Δρ，得到一个新的指标 Δπ，即

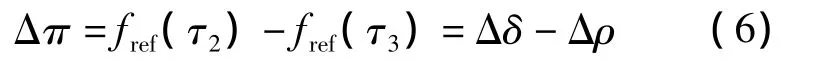
式中，Δπ表示了以自由工况B点为基准时，部件随热力参数的变化而产生的性能指标变化.式(4)亦可改写为

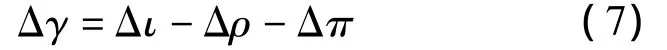
由于经过了对阀门开度影响和部件相互影响的2次过滤，Δγ即为该部件性能指标的实际变化量.因此，在获得一个部件特性曲线的情况下，就可以利用Δρ和Δπ计算出Δγ，从而对该部件进行故障诊断.

Δρ可以通过验收试验或设计数据建立机组的变工况热力特性模型［12］来获得.Δπ则可利用微分方法逼近求得［13］，如图1所示，在自由工况B点上作切线BE，利用E点近似逼近D点，切线BE的斜率为B点处的导数dκ/dτ.特性曲线的函数关系可以通过在自由工况热力参数点τ3附近对一系列独立热力参数τk求偏导近似得到;相应的Δπ为

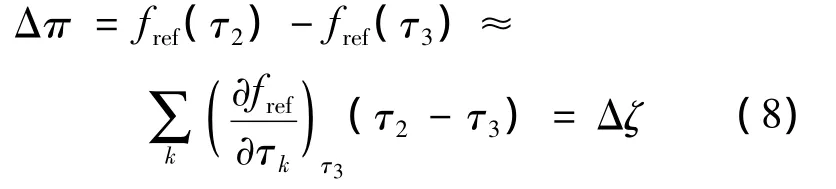
式中，Δζ为Δπ的近似值，在图1中表示为B，E两个状态点的性能指标之差;Δζ与Δπ的差值为ε，即用式(8)计算Δπ时产生的误差为

联立n个如下方程可求解出n个偏导数，即为式(8)偏导项的近似值:

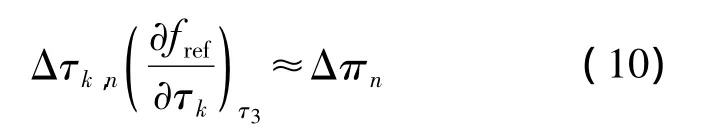
式中，n表示自由工况点附近的一系列无故障工况数，其数值等于τk.

当将Δζ近似代替Δπ时，考虑到式(9)的误差项，引入指标Δγ的近似值Δκ作为判断部件故障的标准.由式(7)～(9)可得Δκ的表达式为

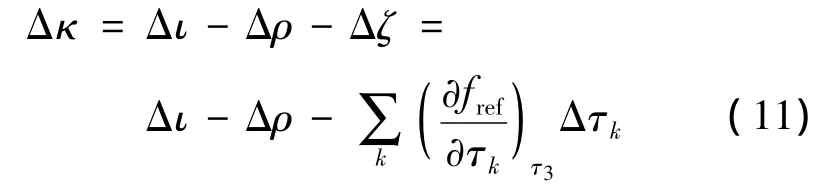
Δκ与Δγ同样作为部件性能指标的实际变化量，可以实现各部件之间相互影响的解耦，从而对部件进行故障诊断，两者误差为ε.

2 热力参数与性能指标的选取

以上定性分析了利用热力参数-性能指标曲线进行故障诊断的原理和方法，但要定量计算出性能指标变化量Δκ，真正实现诊断，还需针对热力系统中具体部件选取合适的热力参数与性能指标.

2.1 热力参数的选取

选取某部件热力参数τ的基本原则是:该参数必须是能够描述该部件运行特性的一组独立变量［14］，如压力、温度、流量等.此外，由于包含了一个部件运行特性的大量信息，文献［15］尝试只将部件的进出口 流作为变量，将特性指标表示为

流的函数.但是，不同的压力、温度、流量等热力参数可能会得相同的 流，这就造成了热力参数信息的缺失，无法获得性能指标对于一组完整热力参数的函数关系.选取热力参数的基本原则应该是保证某一部件的参数个数等于该部件的自由度数，且每个热力参数相互独立.

2.2 性能指标的选取

性能指标κ是能够量化部件在运行过程中性能的变量，如汽轮机的内效率、加热器的端差等.但这些指标并不统一，需要针对各个部件分别选取;当部件发生性能下降时，其热力参数-性能指标曲线可能会与参考工况下的曲线相交，造成部件存在故障，而其性能指标变化量为0的情况.因此，需要选取一个既能对各部件运行特性进行定量分析，又能在部件存在故障时保证Δκ的绝对值严格为正数的统一变量作为性能指标.

引入热经济学结构理论中的变量不可逆损失作为部件的性能指标κ.一个部件的故障与其他部件在该部件产生的诱导故障相加即为不可逆损失.不可逆损失量化了一个部件的流量和能量信息，与部件的能量转化过程的效率直接相关;而且，由于部件的故障会使其产生的不可逆损失比参考工况产生的不可逆损失大，因此用不可逆损失作为性能指标所表示的特性曲线，在部件存在故障时一定会朝该部件运行特性变差的方向发展，从而避免了与参考工况特性曲线的相交.

在热经济学结构理论中，根据部件在火电厂热力系统中的功能，将各部件输入、输出的实际物流通过组合或者分解得到多个燃料()流(F)和一个产品()流(P)，由此可以将实际系统的物理流程图转化为由燃料-产品所表示的生产结构图.图3为某330 MW火电机组热力系统图对应的生产结构图.

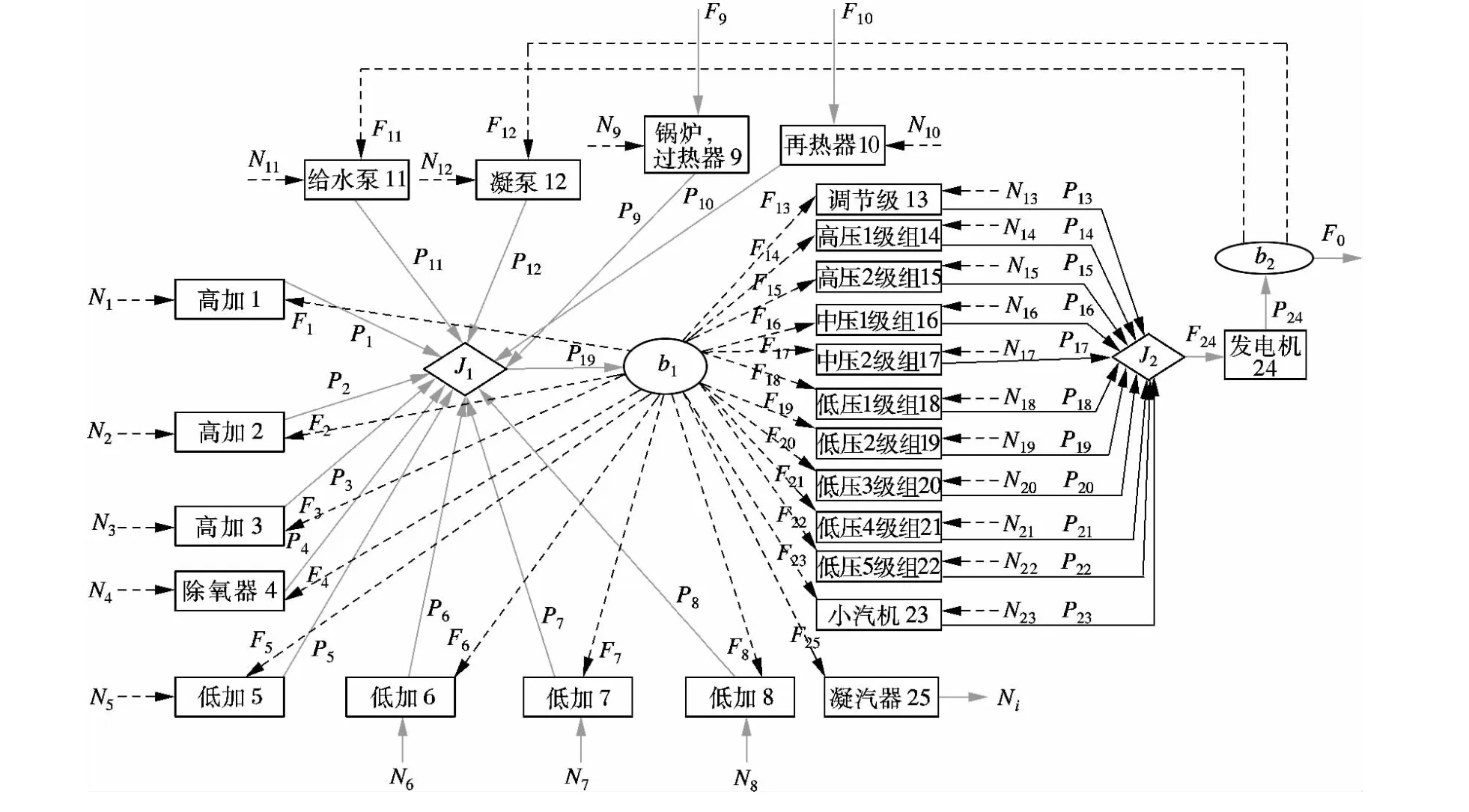
图3 热经济学诊断模型燃料/产品生产结构图

图中，矩形表示物理(生产或耗散)组件，J1，J2表示汇集组件，b1，b2表示分支组件，Fi(i=0，1，…，25)表示该单元所消耗的燃料，Pi(i=1，2，…，24)表示该组件所获得的产品，Ni(i=1，2，…，23)表示该组件所消耗的负熵［16］.汇集和分支组件、入口和出口的 或负熵保持守恒.图3中，圆形和菱形均为虚拟部件，只起连接作用.

通过图3可以看出，一个部件的产品可能是其他部件的燃料或者是电厂整个产品的一部分，即

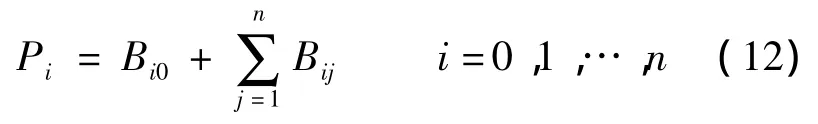
式中，Bij为第i个部件产品中作为第j个部件的燃料;Bi0表示电厂整个产品中第i个部件的产品.

定义单位 耗为某个设备为获得一个单位产品而需要从其他组件中得到的产品数量，即获得第j个部件一个单位产品时，需要第i个部件付出的产品，即

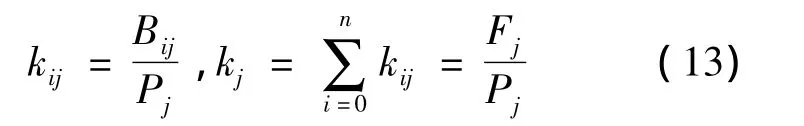
通过单位 消耗，式(12)可以表示为

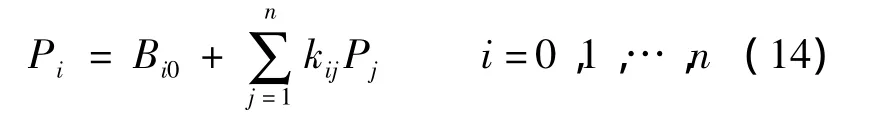
根据结构理论［17］，式(14)亦可写成如下矩阵形式:

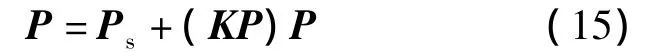
式中，P={P1，P2，…，Pn}T，Ps={B10，B20，…，Bn0}T，KP为一个n×n矩阵，它的元素为单位 耗kij.对式(15)进行矩阵变换，可将每个部件的产品P表示为单位消耗KP和系统最终产品Ps的函数，即

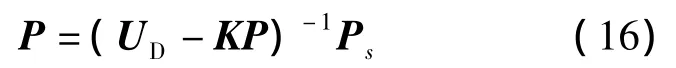
式中，UD为n×n单位矩阵.

对于某一部件的不可逆损失Ii，可表示为该部件输入燃料Fi与输出产品Pi的差值，即Ii=Fi－Pi.当系统部件较多时，为方便计算，亦将其表示为矩阵形式，即

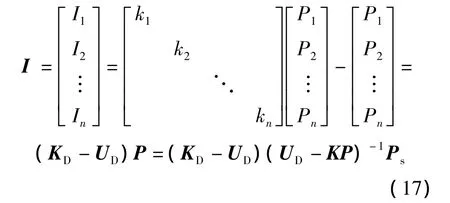
式中，KD为包含每一个部件单位 消耗的对角阵.

通过上述方法可以求得不同工况下热力系统各个部件的不可逆损失，作为部件的性能指标κ;然后针对具体部件选取合适的热力参数τ，根据式(11)可定量求得Δκ，最后可实现对部件的故障诊断.

3 实例分析

将上述模型应用于某330 MW火电机组的性能诊断.汽轮机组型号为N330-16.67/538/538，通流部分由1个高压缸、1个中压缸、2个低压缸、1个凝汽器、1个小汽机组成，回热系统由3个高压加热器、1个除氧器、4个低压加热器、1个疏水冷却器、1个轴封加热器、1个给水泵和1个凝结水泵组成.1#加热器为抽汽压力最高的加热器，依此类推，7#加热器为抽汽压力最低的加热器，各加热器间采用疏水逐级自流连接.

本文基于APROS平台建立该机组汽轮机及热力系统模型，模拟该机组不同工况下的运行.APROS属分析型模型，对各种复杂工况的模拟具有较高的可信度.

将所建APROS模型分别模拟参考工况、定功率条件下的3种故障工况、与故障工况阀门开度相同的无故障工况(即自由工况点)，以及若干自由工况点附近的无故障工况，得到各部件在不同工况下的热力参数.参考工况选择无故障时的热耗保证工况(THA).自由工况点附近的无故障工况通过调整主蒸汽流量获得.3种故障工况包括:① 调节级和中压缸一级组效率下降5%;②2#高加堵管10%和故障工况1同时发生;③80%变工况时调节级、高压缸一级组效率下降5%，且3#高加堵管10%.由于这3种工况分别模拟了机组实际运行中常见的故障，且考虑了变工况发生故障的情况，因此对其的诊断结果具有一定的代表性.

以故障工况1为例，将机组分为若干个需要诊断的部件，利用APROS模拟的热力参数计算出不同工况下图3中的每股 流值，并按式(17)计算出各部件在参考工况、故障工况和自由工况下的不可逆损失.如调节级(C-S)在3种工况下的不可逆损失分别为 IC-S，ref，IC-S，mal和 IC-S，free，分别对应图 1和图2中的状态A点、C点和B点.则式(2)中的Δι可改写为

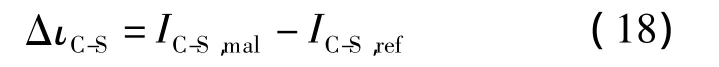
式(5)中的Δρ为

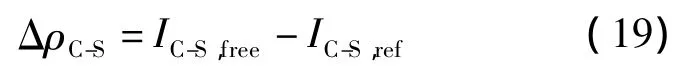
依据前文所述原则选取调节级入口蒸汽压力p1、入口蒸汽温度t1、出口蒸汽压力p2和入口流量D作为热力参数.利用4个自由工况点附近的无故障工况(op1，op2，op3和op4)获得4组热力参数值及不可逆损失;将它们分别与自由工况下对应的热力参数值及不可逆损失相减，可得一系列Δτ和ΔI.根据式(10)可得如下的矩阵:

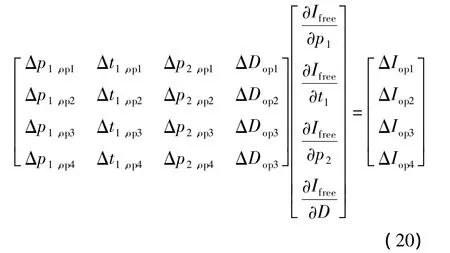
通过求解式(20)可得4组偏微分项∂Ifree/∂τk，将其与式(11)、(18)、(19)联立即为调节级的性能指标实际变化量Δκ，即

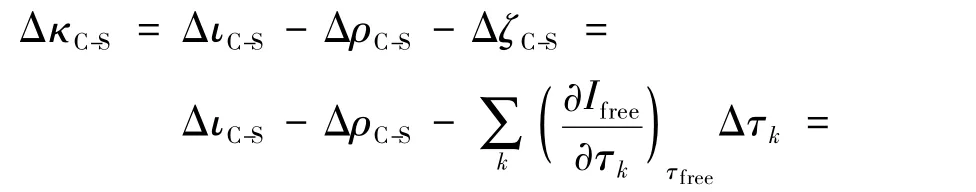
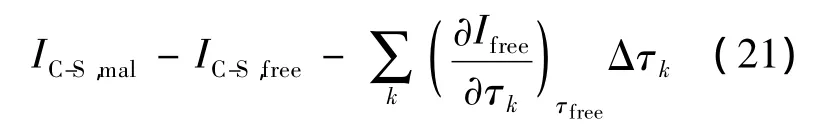
式中，Δτk为故障工况下调节级的4个热力参数值与自由工况下对应参数之差.

在本文计算中，汽轮机其他级组热力参数的选取与调节级相同;而加热器的热力参数则选用入口水压力、入口水温度、出口水压力、出口水温度和抽汽流量;过热器和再热器选用出口蒸汽压力、蒸汽流量和入口工质压力;各类泵选用入口工质压力、温度和流量;凝汽器选用进汽压力、进汽焓、凝结水压力和流量.在自由工况点附近模拟的无故障工况数应与各部件选取的热力参数数相等.另外，由于故障工况3为变工况下发生的故障，因此其对应的参考工况选择80%热耗保证工况，功率亦保持在80%额定功率.

根据上述方法分别定量计算出3种故障工况下系统中各部件的性能指标变化量，故障工况1的计算结果见表1.

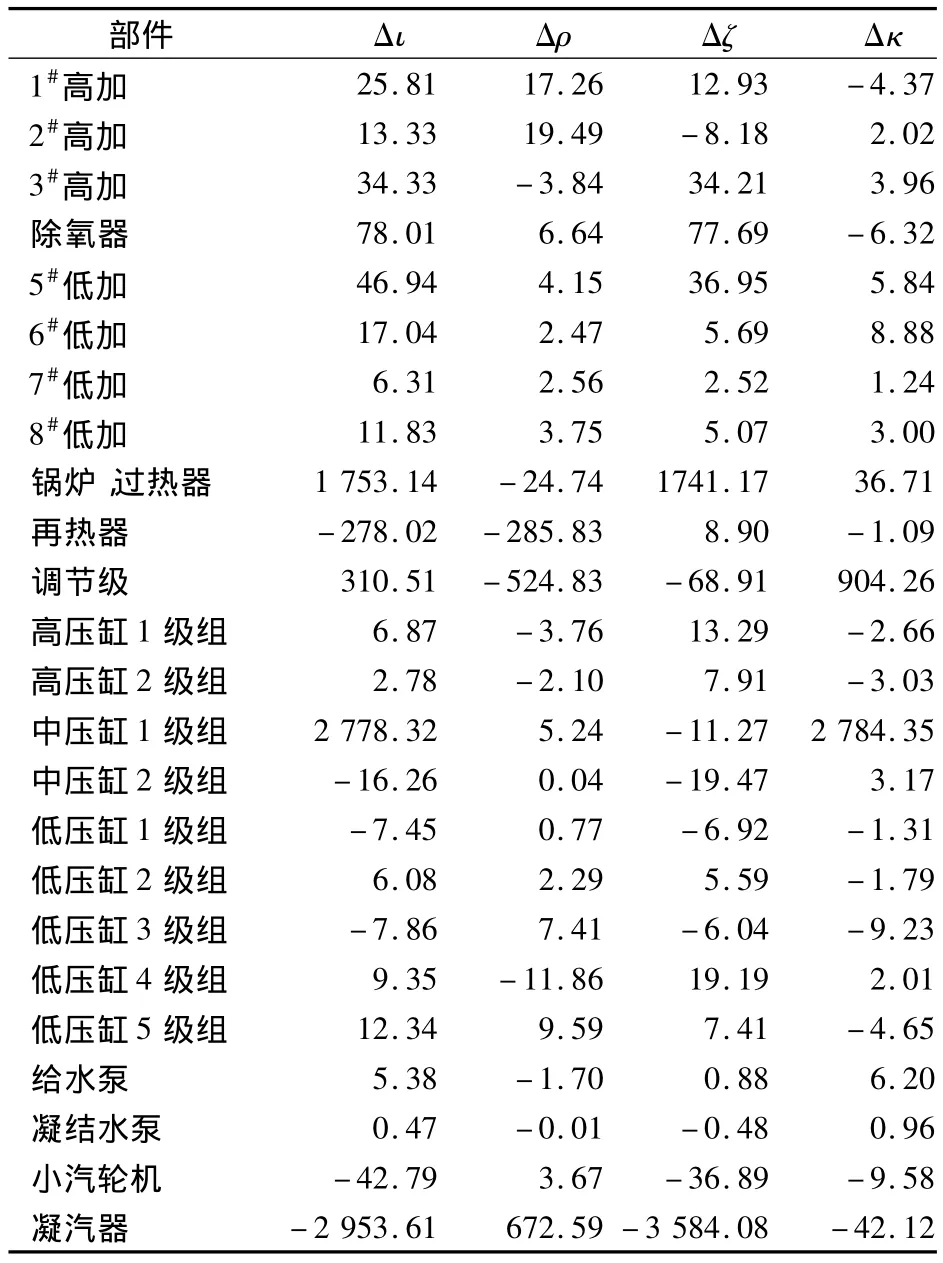
表1 故障工况1各部件的性能指标变化 kW

为更加清楚形象地表现所提出的方法和思想，以调节级为例，将3种故障工况下调节级的计算结果用图4定量表示.以故障工况3为例，A点为未发生故障的参考工况点，当保持机组功率一定，会得到故障工况下的状态C点;但AC段并不能代表由于调节级效率下降引起的真正指标变化，因此还应考虑在参考工况下与C点具有相同边界条件的状态D点，AC段与AD段之差才是由调节级故障造成的实际指标变化.在定功率的情况下，调节汽门开度的变化会对性能指标造成干扰，因此还需将调节级的影响过滤，从而引入自由工况B点，即假想的与工况C点阀门开度相同的无故障工况点.由计算结果可看出，B点相对于A点功率增加、性能指标发生变化;以B点代替A点作为参考基准，则消除了阀门开度影响的指标变化，即为BCD的过程.

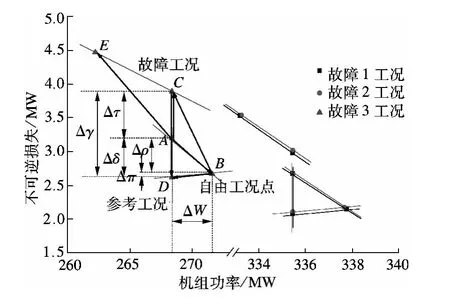
图4 3种故障工况下调节级性能指标变化图

通过上述定量分析可以得到以下结论:

1)3种故障工况下各故障部件会对其他非故障部件造成影响，产生诱导故障.如表1所示，故障工况1中，由于调节级故障，导致高压缸排汽焓上升，再热器吸热量减少，故不可逆损失为负值;同时高压缸排汽焓增加会导致高压缸出力不足，为保证出力一定，需要增加流量，使锅炉内吸热量增加，故不可逆损失为正值;中压缸1级组故障最终引起低压缸排汽焓升高，凝汽器冷源损失增加，故产生较大不可逆损失，其值为负是由于含有凝汽器的系统中存在负熵［16］.故障工况2中，2#高加端差增大会使1#高加存在较大的不可逆损失.同样，在故障工况3下，3#高加的故障也会影响2#高加;高压缸调节级和1级组的效率下降会对各汽缸排汽焓造成影响，从而影响锅炉、再热器以及凝汽器的吸热量，引起不可逆损失的大幅变化.

因此，某一部件不可逆损失较大并不意味着该部件内部发生了真正的故障，其他部件故障有可能在该部件诱导产生不可逆增加.

2)通过引入Δρ和Δζ，对性能指标变化量进行2次过滤，基本可以消除故障部件对非故障部件产生的诱导故障，即非故障部件的Δκ应全部为0.而表1中非故障部件的Δκ值虽然明显小于故障部件，但都没有变为0.这可以理解为存在误差ε.

4 结论

1)提出的基于特性曲线模型能够从理论上消除阀门开度变化的影响及部件在热力参数变化时必然会产生的性能指标变化，定性分析出部件由于其自身故障引起的性能指标实际变化量.通过严格的数学推导和直观分析从理论上基本消除了其他部件的影响，即诱导故障，实现了各部件之间相互影响的解耦.

2)引入热经济学结构理论中不可逆损失作为模型的性能指标，通过定量计算热力系统各部件在故障工况下的不可逆损失变化量，来判别部件是否发生故障.通过实例计算分析不同故障工况下各部件不可逆损失增加量的变化规律，初步证明了提出的思想和模型的可行性.

3)除不可逆损失外，还可选取其他既能对各部件运行特性进行定量分析，又能在部件存在故障时保证其变化量的绝对值严格为正数的统一变量作为模型的性能指标.

本文提出的诊断模型只讨论了恒定功率的情况，而在实际运行中故障工况可能既非定功率，又非定流量，这时需要选定新的基准点来对模型进行改进.另外模型的准确性和对实际运行故障诊断的正确性有待于在之后的研究中继续探讨.

References)

［1］Valero A，Torres C，Lerch F.Structural theory and thermoeconomic diagnosis.Part Ⅲ:intrinsic and induced malfunctions［C］//Proceedings of ECOS.Japan，Tokyo，1999:8-10.

［2］王清照，肖卫杰，王加璇.运用热经济学结构理论进行故障诊断的探讨［J］.中国电机工程学报，2003，23(9):178-181.Wang Qingzhao，Xiao Weijie，Wang Jiaxuan.An inquity into the application of the structural theory for diagnosing malfunction in a thermal system［J］.Proceedings of the CSEE，2003，23(9):178-181.(in Chinese)

［3］王勇，纪冬梅，郑莆燕，等.基于热经济学结构理论的汽轮机组回热系统故障定位研究［J］.动力工程学报，2013，33(1):71-75.Wang Yong，Ji Dongmei，Zheng Puyan，et al.Fault location on regenerative system of turboset based on structural theory of thermo-economics［J］.Jouanal of Chinese Society of Power Engineering，2013，33(1):71-75.(in Chinese)

［4］Liu Y K，Peng M J，Xie C L，et al.Research and design of distributed fault diagnosis system in nuclear power plant［J］.Progress in Nuclear Energy，2013，68:97-110.

［5］Lozano M A，Valero A.Theory of the exergetic cost［J］.Energy，1993，18(9):939-960.

［6］Torres C，Valero A，Serra L，et al.Structural theory and thermoeconomic diagnosis:partⅠ.on malfunction and dysfunction analysis［J］.Energy Conversion and Management，2002，43(9):1503-1518.

［7］Usón S，Valero A.Thermoeconomic diagnosis for improving the operation of energy intensive systems:comparison of methods［J］.Applied Energy，2011，88(3):699-711.

［8］Verda V，Serra L，Valero A.The effects of the regulation system on the thermoeconomic diagnosis of a power plant.PartⅠ:the diagnosis procedure［C］//Proceedings of the ECOS.Istanbul，Turkey，2001:777-784.

［9］Heo G，Lee S K.Internal leakage detection for feedwater heaters in power plants using neural networks［J］.Expert Systems with Applications，2012，39(5):5078-5086.

［10］Ajami A，Daneshvar M.Data driven approach for fault detection and diagnosis of turbine in thermal power plant using independent component analysis(ICA)［J］.Electrical Power and Energy Systems，2012，43(1):728-735.

［11］Pacheco Ibarra J J，Rangel Hernández V H，Zaleta Aguilar A，et al.Hybrid fuel impact reconciliation method:an integral tool for thermoeconomic diagnosis［J］.Energy，2010，35(5):2079-2087.

［12］曹祖庆.汽轮机变工况运行特性［M］.北京:水利水电出版社，1991:167.

［13］张超.复杂能量系统的热经济学分析与优化［D］.武汉:华中科技大学能源与动力工程学院，2006.

［14］Toffolo A，Lazzaretto A.A new thermoeconomic method for the location of causes of malfunctions in energy systems［C］//ASME Paper IMECE.Washington DC，USA，2003:355-364.

［15］Verda V，Serra L，Valero A.Thermoeconomic diagnosis:zooming strategy applied to highly complex energy systems.Part 2—on the choice of the productive structure［C］//ASME Paper IMECE.New Orleans，Louisiana，USA，2002:215-224.

［16］Valero A，Torres C.Application of thermoeconomics to operation diagnosis of energy plants［M］.Oxford，UK:EOLSS Publishers，2006:181-185.

［17］Shi Y F，Xu J Q，Zhou K Y.Structural theory and thermoeconomic diagnosis:application to a supercritical power plant［C］//Asia-Pacific Power and Energy Engineering Conference.Wuhan，China，2009:1-4.