掺有定形相变胶囊的储能墙体传热性能数值研究

戴晓丽 郑佳宜 陈振乾

(1东南大学能源与环境学院，南京210096)

(2江苏大学能源与动力工程学院，镇江212013)

自20世纪80年代开始，由于考虑节能、环保和利用太阳能的需要，相变材料被掺入到建筑材料中.构筑相变储能围护结构，利用其中的相变材料在相变过程中吸能和释能的特点实现能量的利用与转换，有利于建筑物室内温度的调控，可以大大增强围护结构的蓄热隔热作用，改善室内热环境，达到节能与舒适的目的［1-5］.众多学者对此进行了大量的理论与实验研究，Kim 等［6］和李丽莎等［7］分别对直接混合法和分层插入法制备的定形相变墙体的传热性能进行了数值模拟和实验研究，并与普通墙体进行了对比，结果显示，分层插入法制备的定形相变墙体节能效果更加明显.周国兵［8］用焓法对温度波作用下的建筑内墙板的热特性进行了数值研究，结果表明相变温度是影响室内空气温度波幅衰减的重要因素.可以看出，目前关于相变储能围护结构的研究，重点在于墙板的传热研究，较少考虑室内空气的温度响应.本文以掺有定形相变胶囊［9］(胶囊由高密度聚乙烯/石蜡复合而成)储能墙体作为围护结构的相变房间为对象，并考虑室内空气的热响应，通过建立相变房间传热理论模型，模拟了在周期性变化的室外温度边界条件下，相变储能墙体内的传热过程及室内空气的温度响应.

1 模型建立

1.1 物理模型

图1为相变房间及其相变墙体的结构图.相变房间四周均由相变墙体组成，底部为绝热界面.复合相变墙体结构主要由3部分组成，内外层是普通混凝土墙体层，中间层为相变层，是由高密度聚乙烯(HDPE)/石蜡定形相变胶囊与常规建筑材料混凝土混合制成.

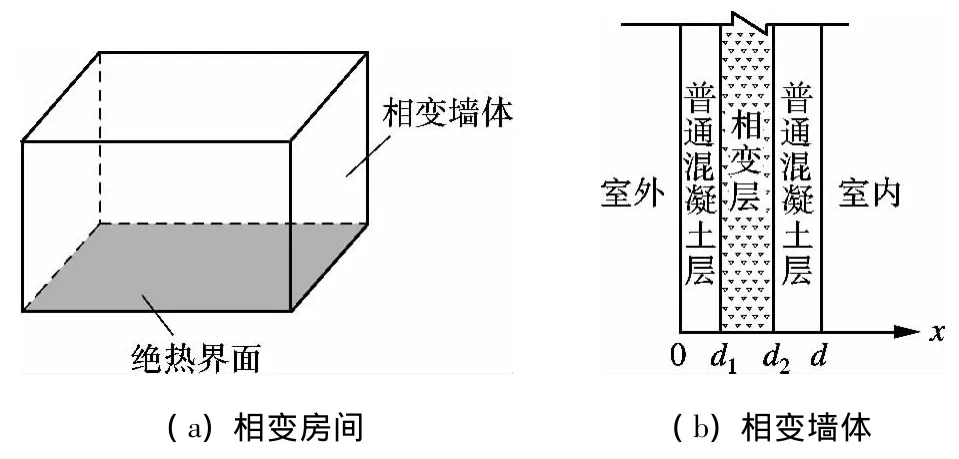
图1 相变墙体与房间的结构示意图

为了方便计算和建立数学模型，这里对相变墙体建立了如图1(b)所示的直角坐标系，并对模型作出如下假设［10］:

1)相变胶囊在混凝土基体中呈均匀分布，并忽略其相变过程中体积变化对墙体的影响.

2)石蜡物性参数(导热系数、比热容)在每相中不随温度发生变化，在处于熔融状态时，参数随温度线性变化.

3)相变储能混凝土内物性参数均匀，且各向同性.

4)由于相变胶囊粒径较小，相变墙体中可忽略对流的影响，即相变墙体的传热过程可简化为纯导热过程.

5)墙体的厚度远小于其宽度与高度，认为沿高度和宽度方向温度变化很小，只沿厚度方向变化，即其传热过程为一维导热过程.

6)室内各处的空气温度均匀一致，即室内空气作为整体考虑.

1.2 数学模型

为了便于分析，仅考虑在室外温度波作用下，室内空气与其相变墙体之间的热传递过程(其辐射换热可当量为等效温度的形式)，室外温度波在297～306.2 K之间按余弦波周期24 h变化，假定室内各处的空气瞬时、均匀一致地发生变化，即将室内空气作为一个整体来考虑，下面分别建立相变墙体内部以及墙体内表面与室内空气之间的热传递平衡方程.由于石蜡融化相变具有一定的温度范围，在介质内部将存在固相区、糊状区(固液共存区)和液相区3个不同性质的状态区.本文采用显热容法［8］在整个墙体区域建立统一的数学模型.

1)相变墙体

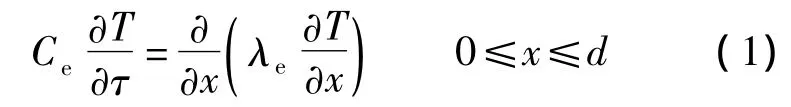
2)室内

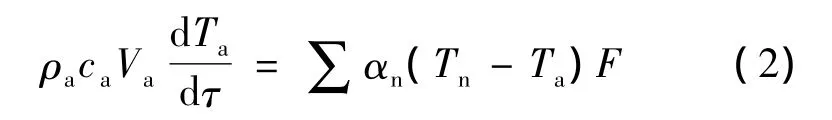
3)边界条件

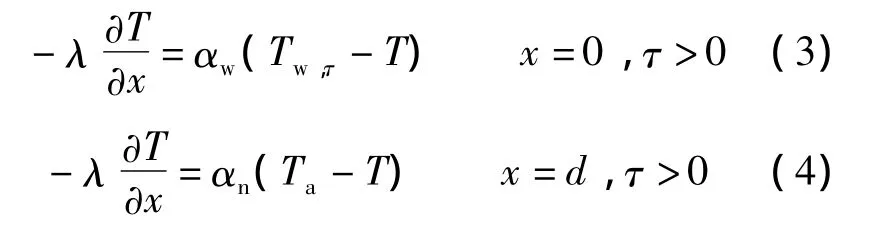
4)初始条件

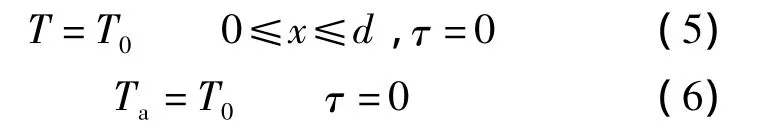
式中，Ce为墙体相变等效热容;F为墙体表面积;V为室内体积;α为对流换热系数;τ为时间;T为温度;T0为初始温度;下标 a，n，w分别表示室内空气、室内壁面和室外壁面.

墙体相变层等效热容Ce采用质量加权平均表示［11］，即

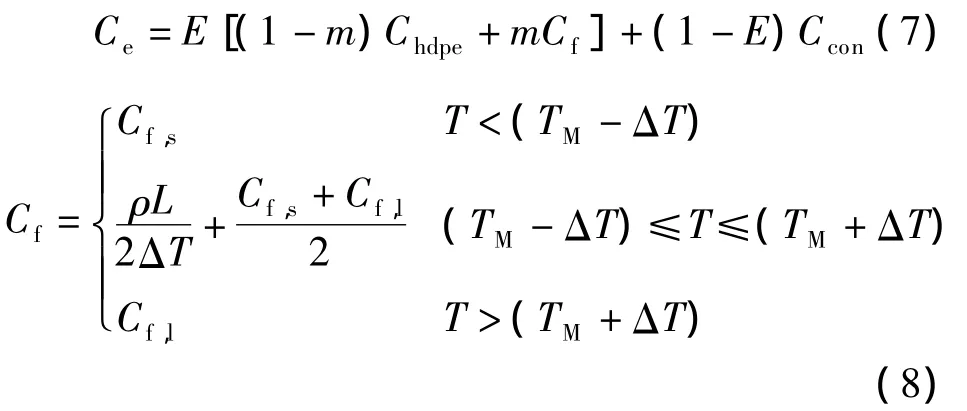
采用基于球形分散相的复合材料Maxwell-Eucken模型计算墙体相变层等效导热系数［12］，即

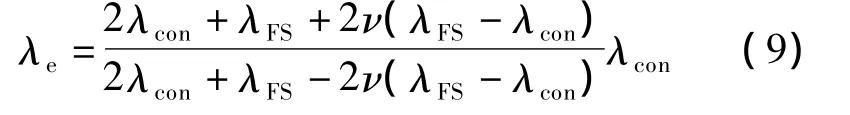
其中

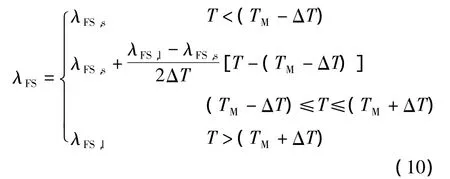
式中，m为定形相变胶囊中的石蜡质量分数，取m=50%;E为定型相变胶囊在相变混凝土中的质量含量;v为定形相变胶囊材料的体积分数;TM为相变中心温度;ΔT为相变温度波动幅度;L为石蜡的相变潜热，取 L=192 kJ/kg;下标 f，l，s，hdpe 和 con分别表示相变材料、液相、固相、高密度聚乙烯和混凝土.材料的物性参数见表1.

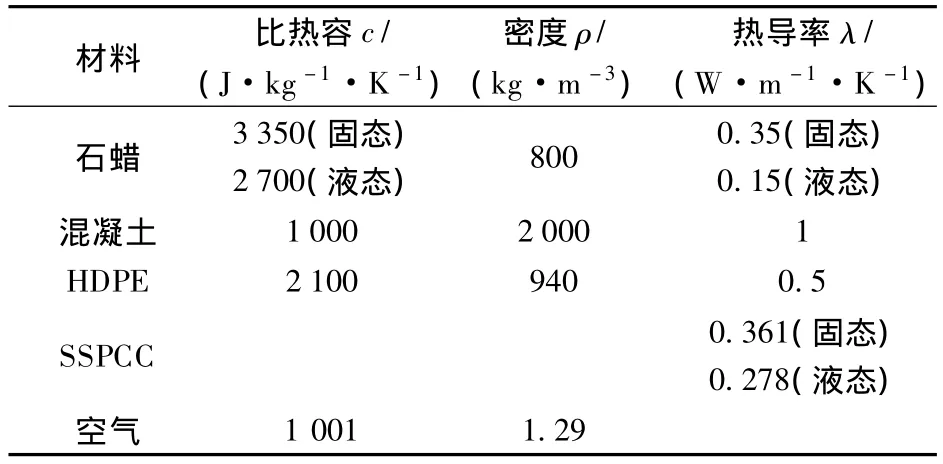
表1 材料的物性参数

2 数值模拟

采用控制容积法求解上述变物性非稳态导热问题方程组，采用先节点后界面的方法进行区域离散，然后进行超松弛高斯赛德尔迭代求解［10］，其中松弛因子取为1.5.

模型中对网格的相关性进行了分析，时间步长逐渐缩小到600 s，当网格数为48单元时，网络数对数值模拟结果的影响已相对较小.为了验证模型的正确性，本文采用该模型的计算结果与 Kim等［6］采用焓法的计算结果进行了比较，如图2所示.由图可以看出，两者的结果基本吻合，误差在5%之内.

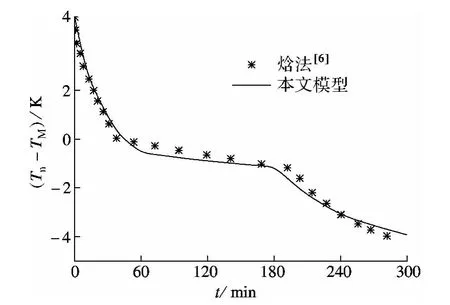
图2 2种模型计算结果比较

3 模拟结果与讨论

3.1 相变墙体的内部温度分布

图3显示了当定形相变胶囊含量在60%，相变温度为(299±1)K时，在外界周期性温度波的作用下，作用时间t=15 h时不同相变墙体厚度下墙体内部温度场分布.从图中可以很明显地看出，墙体的显热-潜热-显热三段储能过程.如相变墙体厚度d为8 cm，其相变材料的潜热储存发生在8～16 cm段混凝土层之间，该层的温度波传递速率明显减缓.正因为这层相变混凝土层的存在，当受到来自于外界温度波的热作用时，该层相变材料周期性地发生融化-凝固过程，吸收/释放大量的潜热，阻碍了热流在混凝土层中的传递.图3为墙体受外界周期性温度波作用15 h，相变材料的温度分布.由图可见，相变墙体越厚，因其蓄积吸收的潜热量较高，热惰性较大，则内层的温度越低，因而较厚的相变墙体具有明显的节能意义.

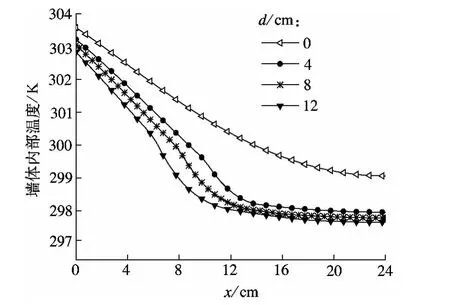
图3 墙体相变层厚度对内部温度分布的影响

3.2 定形相变胶囊含量对室内空气温度的影响

图4为墙体相变层厚度为8 cm、相变温度为(299±1)K时，相变墙体中定形相变胶囊的质量分数对室内空气温度的影响.从图中可以看出，在室外温度波的不断热作用下，室内空气温度逐渐增加，达到稳定状态时，呈现出周期性波动.不含有定形相变胶囊的房间其室内空气的温度从作用时刻开始一直呈现出较高的温度状态，且波幅最大，温度峰值也最高.这里以非相变房间的室内空气温度为基准参数，定义衰减度f为相变房间的室内空气温度波幅与非相变房间的室内空气温度波幅之比，时间延迟ψ为相变房间的室内空气温度波对非相变房间室内空气温度波的相位滞后［6］.从图4可以看出，定形相变胶囊质量含量为30%，60%的相变房间的衰减度分别为90.7%和77.6%，时间延迟分别为1和2 h.随着定形相变材料的不断掺入，定形相变胶囊质量含量从0%增加到60%，室内空气温度波的波幅衰减度逐渐增加，相位延迟时间也逐渐延长，有效地调节了室内空调设备的容量，节约了空调设备的能耗.因此综合图3和图4可以看出，储能墙体中的相变胶囊含量是影响室内空气温度衰减的重要因素之一.

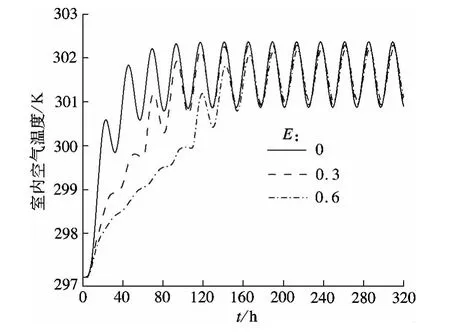
图4 定形相变胶囊含量对室内空气温度的影响

3.3 相变中心温度对室内空气温度的影响

当墙体相变层厚度为8 cm，定形相变胶囊含量为60%，相变温度波动幅度1 K，室外温度在297～306.2 K之间呈周期性振荡时，图5分析了当相变中心温度从299 K变化到303 K时，室内空气温度的变化.从图中可以看出，相变中心温度为299 K时，初始阶段室内温度提升较慢，这是因为该相变中心温度下的材料较早发生相变，缓和了室内空气温度.相变中心温度为303 K的相变材料其相变发生最晚，初始阶段室内空气温度升温速率最快.但最终稳定状态下，处于相变温度301 K附近的相变房间，其室内空气温度波动较小，均值也较低，而相变中心温度较低的299 K和较高的303 K的相变空间的室内空气温度则发生了较大幅度的波动.同时，从图6为不同相变中心温度下的相变层中心位置的温度变化曲线中可以看出，稳定状态时，该相变层所在位置的温度幅度基本围绕在301 K平衡点附近振荡，因此，该温度即可认为是相变中心温度的最佳取值点，这与文献［13］中得到的结论相吻合.因此，选择合适的相变中心温度对提高蓄能效果有着非常重要影响.

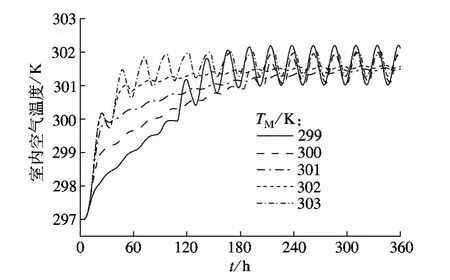
图5 相变中心温度对室内空气温度的影响

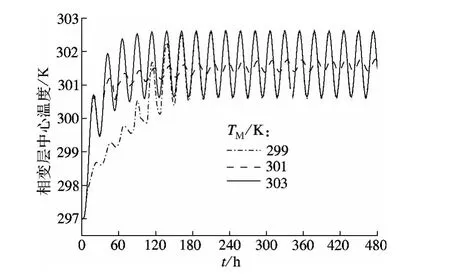
图6 相变层中心位置(x=0.2 cm)的温度曲线

3.4 相变中心温度波动幅度对室内空气温度的影响

图7(a)描述了当墙体相变层厚度为8 cm，定形相变胶囊含量为60%，相变中心温度在301.5 K时，相变温度波动幅度对室内空气温度的影响.从图中可以看出，相变温度波动幅度为0.1 K时，室内空气温度基本保持在301.5 K左右，相变温度波动幅度越大，室内空气温度波动幅度则越大，如相变温度波动幅度为4 K时，其室内空气温度一直处于301.4～301.8 K之间振荡，这是因为相变温度波动幅度区间的增大，使得融化温度较低，凝固温度更高，该相变层的温度波较早地触发了相变材料的融化-凝固过程，此时对室内空气温度的影响也会更加显著，但振荡平衡温度基本一致.

图7(b)是当墙体相变层厚度为8 cm，定形相变胶囊含量为60%，相变中心温度在299 K时相变温度波动幅度对室内空气温度的影响.当相变层发生相变时，较小的相变温度波动幅度，能使得室内空气温度长时间地保持在一稳定值附近，如相变温度波动幅度为0.2 K时，室内空气温度在30～100 h时间内基本保持在298.8～299.2 K范围内，且变化幅度较小.相变温度波动幅度越大，则室内空气温度波动幅度越大，如相变温度波动幅度为1 K时，其室内空气温度一直处于从298至300 K缓慢爬升的状态.虽然相变温度波动幅度不同，但其材料的相变潜热值是不变的，因此当室内温度达到稳定状态时，此时相变层的平均温度(301.5 K)已超越相变温度，相变材料完全融化，即使相变温度波动幅度不同，其室内空气温度波动变化也基本保持一致.

综合前述不同相变温度条件下的因素分析可见，相变温度波动幅度的大小仅影响了室内空气温度的波动区间，而对振荡的平衡温度影响较弱.

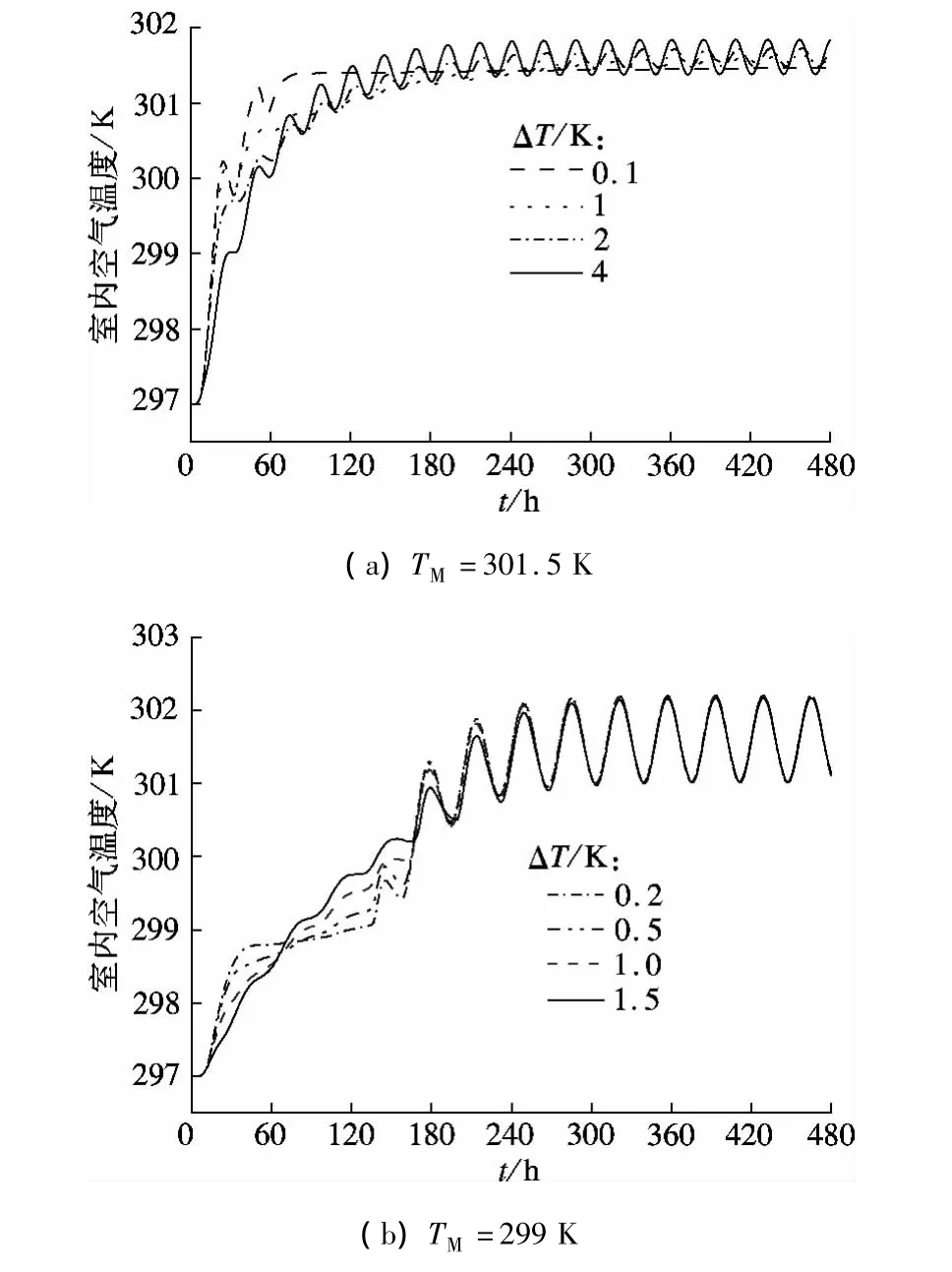
图7 相变温度波动幅度对室内空气温度的影响

4 结语

1)储能墙体中的相变胶囊含量是影响室内空气温度衰减的重要因素之一，含量越高，相变层厚度越厚，节能效果越明显.

2)选择合适的相变中心温度的相变材料对提高蓄能效果非常重要，相变中心温度的最佳取值点宜尽量接近墙体相变层中心温度，有助于较好地发挥其相变材料的功能，更好地提高室内空气温度的稳定性.

3)相变温度波动幅度的大小仅影响了室内空气温度的波动区间，而对振荡的平衡温度影响较弱.所得结果对相变材料在墙体中的应用起到一定的指导意义.

References)

［1］Hadjieva M，Stoykov R，Filipova T Z.Composite salthydrate concrete system for building energy storage［J］.Renewable Energy，2000，19(1/2):111-115.

［2］Feldman D，Banu D，Hawes D W.Development and application of organic phase change mixtures in thermal storage gypsum wallboard［J］.Solar Energy Materials and Solar Cells，1995，36(2):147-157.

［3］Hadjieva M，Kanev S，Argirov J.Thermophysical properties of some paraffins applicable to thermal energy storage［J］.Solar Energy Materials and Solar Cells，1992，27(2):181-187.

［4］Eddhahak-Ouni A，Colin J，Bruneau D.On an experimental innovative setup for the macro scale thermal analysis of materials:application to the phase change material(PCM)wallboards［J］.Energy and Buildings，2013，64:231-238.

［5］Sharma A，Shukla A，Chen C R，et al.Development of phase change materials for building applications［J］.Energy and Buildings，2013，64:403-407.

［6］Kim J S，Darkwa K.Simulation of an integrated PCM—wallboard system［J］.International Journal of Energy Research，2003，27(3):215-223.

［7］李丽莎，闫全英.添加石蜡的相变水泥墙传热性能分析［J］.太阳能学报，2012，33(1):126-128.Li Lisha，Yan Quanying.Research on the thermal performance of the phase change material concrete wall［J］.Acta Energiae Solaris Sinica，2012，33(1):126-128.(in Chinese)

［8］周国兵.温度波作用下建筑内墙定型相变材料板的热特性［J］.太阳能学报，2011，32(8):1211-1216.Zhou Guobing.Thermal behavior of shape-stabilized phase change material at internal building walls with temperature waves［J］.Acta Energiae Solaris Sinica，2011，32(8):1211-1216.(in Chinese)

［9］戴晓丽，王登云，陈振乾，等.球形相变胶囊内凝固传热过程的数值模拟［J］.工程热物理学报，2013，34(4):715-719.Dai Xiaoli，Wang Dengyun，Chen Zhenqian，et al.Numerical study on Solidification heat transfer of spherical phase change capsule［J］.Journal of Engineering Thermophysics，2013，34(4):715-719.(in Chinese)

［10］郭宽良，孔祥谦，陈善年.计算传热学［M］.合肥:中国科学技术大学出版社，1988:30-85.

［11］陈德鹏，钱春香，王辉，等.水泥基材料比热容测定及计算方法的研究［J］.建筑材料学报，2007，10(2):127-131.Chen Depeng，Qian Chunxiang，Wang Hui，et al.Research on determination and calculation method of specific heat capacity of cement-based materials［J］.Journal of Building Materials，2007，10(2):127-131.(in Chinese)

［12］Agari Y，Uno T.Estimation on thermal conductivities of filled polymer［J］.Journal of Applied Polymer Science，1986，32(7):5705-5712.

［13］钟志鹏，张寅平，江亿.相变墙板布置位置及相变温度对其使用效果的影响［C］//2000年暖通空调学术论文集.北京，2000:347-350.Zhong Zhipeng，Zhang Yinping，Jiang Yi.The influence of the location of the phase change wallboard and the phase change temperature on the using effect［C］//ProceedingsofHVAC'2000 Conference. Beijing，2000:347-350.(in Chinese)