丝状颗粒在滚筒横向截面中的传热传质特性

朱立平 秦 霞 袁竹林 闫亚明 罗登山 李 斌

(1东南大学能源热转换及其过程测控教育部重点实验室，南京210096)

(2中国烟草总公司郑州烟草研究院烟草工艺重点实验室，郑州450001)

(3扬州大学水利与能源动力工程学院，扬州225127)

滚筒干燥器因其具有适用范围广、生产能力强、运转可靠、操作弹性大等优点，而被广泛应用于化工、能源、食品、建材等诸多领域.

早期转筒干燥机内物料传热传质特性的研究主要得出了一些具有一定使用范围的经验或半经验公式.20世纪80年代之后，随着研究的进一步深入和计算机技术的发展，人们开始建立转筒干燥机内物料干燥的简单数学模型，并利用计算机进行初步模拟［1-3］.但由于物料在滚筒中干燥过程的复杂性以及目前实验测量技术的局限性，难以获得精确且普遍适用的研究结论.因此目前亟需从物料传热传质机理出发来建立适用范围较广的数学模型.近年来，离散单元法逐渐应用于颗粒尺度层面的传热传质特性的研究，取得了通过实验很难得到的颗粒温度演变等信息［4］.Chaudhuri等［5］提出了一种滚筒中颗粒流的传热模型，讨论了颗粒导热系数、滚筒转速、抄板尺寸等参数对传热过程的影响;Chaudhuri等［6］又利用所建模型对回转炉中颗粒的传热问题进行了研究，并将结果与实验进行了比较验证;Shi等［7］将离散单元法与计算流体动力学相结合，模拟了在不同材料、不同颗粒尺寸等情况下，转筒中颗粒的对流与导热问题.

针对上述背景，为了简化研究，突出颗粒传热传质过程的重点，本文将以横向截面单元为研究对象(在该单元中仅考虑颗粒在滚筒中的横向运动，忽略纵向运动)，采用实验与数值模拟相结合的手段，探讨一类具有丝状结构(如纤维、叶丝、牧草、秸秆等)的异形颗粒在滚筒中的传热传质规律，从而为滚筒干燥器的优化设计、最佳运行工况及其性能的改进提供依据.

1 实验

1.1 实验装置

本文建立的小型滚筒干燥装置由热风系统和滚筒系统组成，如图1所示.筒体内径为400 mm，转速为0～20 r/min.物料可从筒体前端的排湿口加入到滚筒内部.筒体内设置4块纵向直线式抄板，安装角度为90°.实验中来自空压机的微量气流由输气管道经加热炉两级加热后再通过筒体后端的布风板注入筒体，在对物料进行干燥后经由排湿口排出.滚筒筒壁温度的调节主要通过控制外固定筒体和内滚动筒体之间的加热油浴的温度来实现.

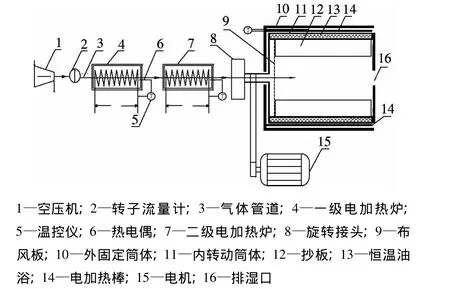
图1 滚筒实验装置系统图

由于本文主要研究滚筒横向截面的颗粒运动及干燥过程，因此实验过程中保持筒体水平，再加上滚筒长度较短，这样可假设筒体纵向空间的每个横向截面单元的外部干燥条件(壁温、气温等)基本一致.滚筒内所有物料的平均温度和含水率的变化过程就可以看作每个横向截面单元内颗粒的平均温度和含水率的变化过程.

1.2 实验方法

实验所采用的物料为经振动筛分仪筛分后尺寸约18 mm的叶丝颗粒，其初始平均含水率大约在22%，初始温度则为20℃.实验开始后，首先设定滚筒内油浴温度、转速和所需热风温度以及热风流量，并采用温湿度计测量气体的相对湿度.当整个系统达到设定值并稳定后，将500 g左右的叶丝一次性加入到滚筒内部，同时开始计时.在预先设定的时间点将物料迅速盛装在一个绝热容器中，该容器的中心装有热电偶，并连接到温度记录仪.当记录仪显示的温度不再快速变化时，读取显示值，将该值作为叶丝的平均温度.此后，再将测量好温度的实验样品迅速装袋密封，于恒温恒湿室中平衡48 h后，采用烘箱法测定物料的平均含水率.重复以上实验步骤，可对不同工况、不同预设时间点的物料平均温度及含水率进行测量.

2 数学模型

2.1 运动模型

由于丝状颗粒的形状偏离球形较大，若将其抽象成球形颗粒进行修正计算，会产生较大误差［8］.因此，根据丝状颗粒长径比较大、柔软、易绕曲变形等特征，将其假设成由若干杆状颗粒和铰约束连接而成的细长链式模型，如图2所示.颗粒段与段之间的运动又通过铰约束相互耦合，从而形成独特的动力学效应，使得该细长链式模型颗粒明显区别于球形颗粒.

实验过程中，由于热风的速度非常小(横截面平均风速0.007 7 m/s)，气流与颗粒相对运动所产生的力可以忽略不计，因此运动模型中仅考虑丝状颗粒的重力、颗粒-颗粒的碰撞力以及颗粒-筒壁、颗粒-抄板之间的作用力.

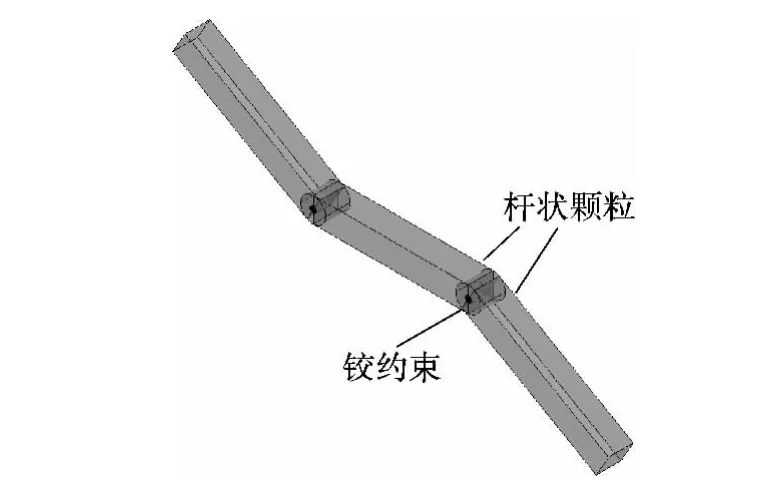
图2 丝状颗粒的链式模型

本文采用离散单元法描述颗粒运动，单个颗粒的平动和转动方程如下［9-10］:

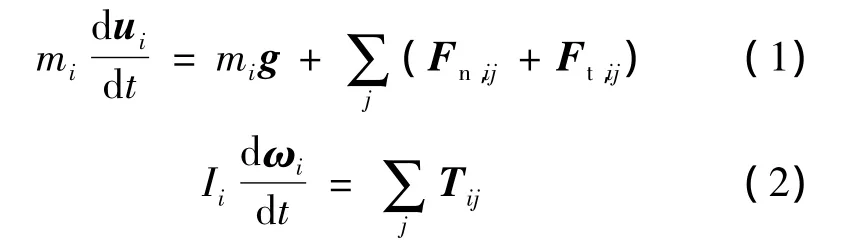
式中，u和ω分别为颗粒的平动速度和转动速度;m为颗粒的质量;i，j表示颗粒;下标n和t分别为法向和切向;g为重力加速度;F为碰撞接触力;T为合力矩;I为颗粒的转动惯量.

碰撞接触力F可根据下式进行求解［11-12］:

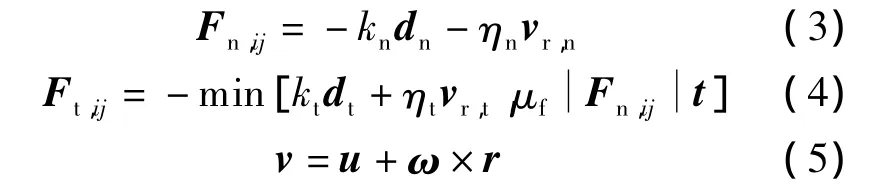
式中，k为颗粒的刚度;d为颗粒相撞所产生的弹性形变;η为阻尼系数;μf为摩擦系数;t为碰撞切向单位矢量;v为颗粒碰撞点的速度;vr为碰撞点相对速度;r为颗粒质心到碰撞点的位置矢量.

2.2 传热模型

在本文所涉及的滚筒干燥过程中由于温度相对较低，可以忽略辐射传热的影响，因此本文中仅考虑颗粒与颗粒(壁面)间的碰撞接触传热以及颗粒与气体之间的对流换热［13］.

2.2.1 颗粒-颗粒(壁面)接触传热

在计算颗粒碰撞接触传热时，假设颗粒与颗粒(壁面)之间的碰撞为弹塑性碰撞.若颗粒i只有一条边与颗粒j相接触(即边与面的接触)，则认为颗粒在碰撞过程中将产生一定的弹性形变，从而在形变处构成一个交界面，而该交界面便为碰撞颗粒间的传热接触面Ac(见图3);若颗粒i有2条边与颗粒j相接触(即面与面的接触)，则传热接触面Ac便为两接触面之间的重合部分.关于丝状颗粒碰撞接触传热模型的详细推导过程，可以参考课题组此前的研究［14］，在此列出最终表达式为

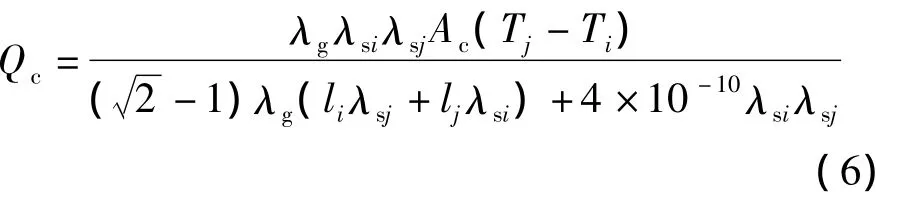
式中，Qc为碰撞传热量;T为颗粒内部的平均温度;l为颗粒中心到碰撞接触面中心的距离;Ac为颗粒间的接触面积;λs为颗粒的导热系数;λg为气体导热系数.

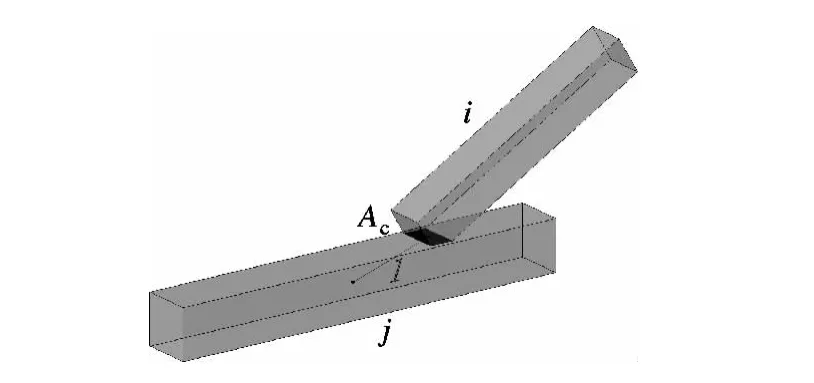
图3 丝状颗粒碰撞传热示意图

2.2.2 颗粒-气体的对流换热

当颗粒处于下落抛洒状态时，由于气流与物料的接触面积大，相对速度高，因此采用强制对流换热模型［15］;当颗粒处于稠密堆积状态时，由于这一阶段物料与热气流的总接触面积小、相对速度小，因此采用自然对流换热模型［16-17］.强制对流换热模型和自然对流换热模型分别为

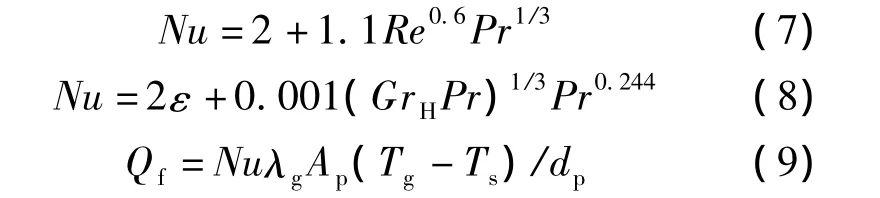
式中，Qf为对流换热量;ε为丝状颗粒的局部堆积孔隙率;Gr为格拉晓夫数;Pr为普朗特数;Nu为努塞尔数;Ap为颗粒表面积;dp为颗粒的等表面积当量直径.在本文的数值模拟过程中，根据以下条件来判断颗粒是处于下落抛洒还是稠密堆积状态:①当颗粒位于筒体中部，即颗粒到筒体中心的距离小于抄板顶端到筒体中心的距离时，则认为其处于下落抛洒状态.②当条件①不成立时，首先将计算区域划分为若干网格，再根据颗粒的位置确定各网格空间的固相容积份额fs，若颗粒所处局部空间为稀相(本文取fs≤0.15)，则认为其处于下落抛洒状态;若颗粒所处局部空间为密相(fs＞0.15)，则认为颗粒处于稠密堆积状态.

2.3 传质模型

根据对流传热和对流传质的类比关系［18］，用舍伍德数Sh取代Nu，施密特数Sc取代Pr，则上述湿物料表面与气体之间对流换热关系可应用于对流传质方程，当颗粒处于下落抛洒状态时，采用如下方程:

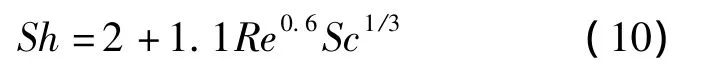
若颗粒处于稠密堆积状态时，则采用

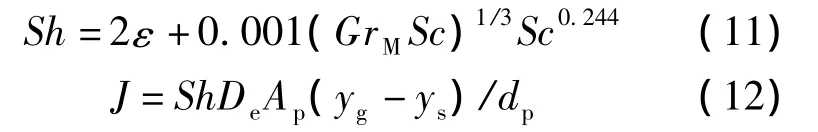
式中，J为传质速率;GrM为自然对流传质格拉晓夫数;De为水分扩散系数;ys，yg分别为颗粒与气流中水分质量浓度.

3 实验与模拟结果分析

3.1 数值计算条件

本文假设在数值模拟过程中，滚筒壁温、气流温度、气流相对湿度等参数保持不变，实验中所采用的湿物料为叶丝，而模拟时将其视为密度均匀的丝状颗粒，由筒体中心处加料，颗粒的速度、角速度和位置均以随机方式给出，采用重力沉降法，令其自然下落，均匀堆积在筒体下部.本文中所涉及的实验气体温度均为100℃，流量为3.5 m3/h，气体含水率近似于0，计算的时间步长为2.5 μs;其他数值模拟计算条件如表1所示.

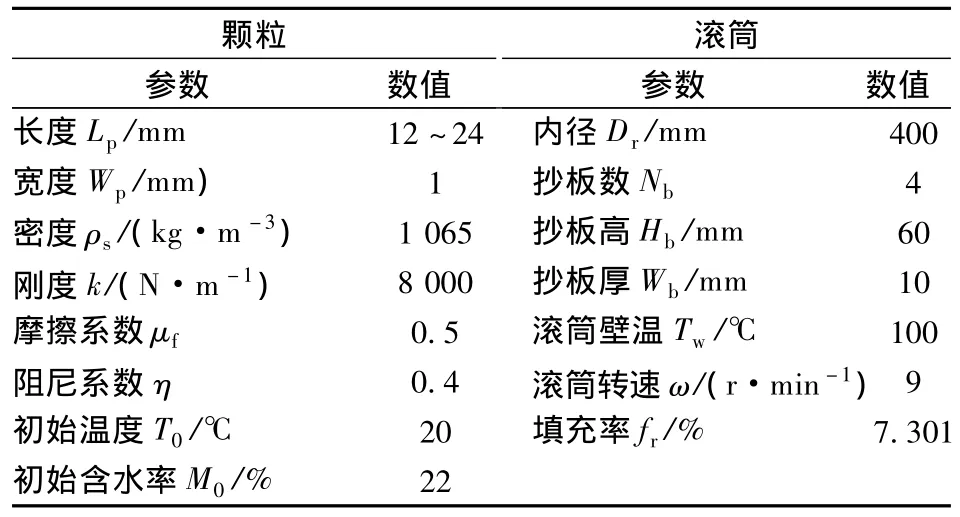
表1 数值计算参数

另外，叶丝颗粒的主要热物性等参数如下.

1)叶丝颗粒导热系数为

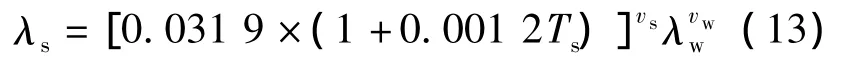
式中，Ts为颗粒的温度，K;λw为水的导热系数，W/(m2·K);vs，vw分别为颗粒中固相骨架以及水分的体积率.

2)叶丝颗粒的比热为

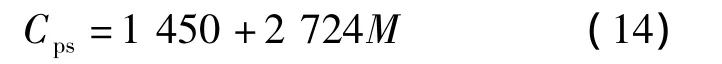
式中，M为颗粒的含水率.

3)叶丝颗粒水分扩散系数为

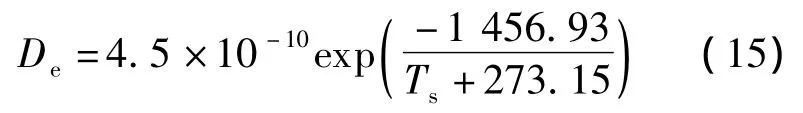
3.2 结果讨论

筒壁温度是滚筒设备的重要操作参数之一，本文分别实验和模拟了滚筒壁温在Tw=80，100和120℃三种条件下的颗粒温度及含水率的变化，如图4所示.可以看出，筒壁温度对叶丝温度和含水率变化的影响比较明显，随着壁温的升高，叶丝温度上升以及含水率下降的速度明显加快.这是由于叶丝所获取的热量主要来自于高温壁面，增大筒壁温度就使叶丝与壁面间的接触换热量增加，所以同一时刻，物料的温度就相对较高.另一方面，较高的筒壁温度，使叶丝能够获取充分的热量来气化水分，因此也就保证了较大的物料含水率下降速度.由图4中的模拟与实验结果的对比可知，虽然二者存在一定的差异，但其变化趋势基本吻合，从而证明了本文所建传热传质数学模型的适用性.

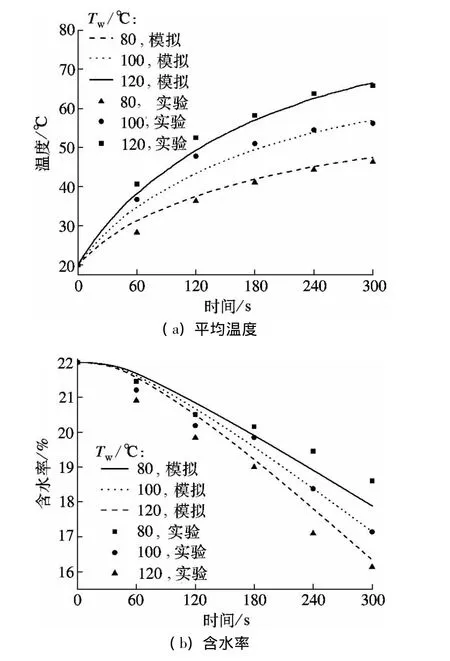
图4 不同筒壁温度下颗粒平均温度和含水率的变化

图5为不同筒壁温度条件下滚筒中丝状颗粒温度分布随时间的变化过程.可以看出，颗粒被抄板扬起并在上升过程中逐渐洒落，在滚筒横向截面形成连续的料幕，随着抄板的升高逐渐被拉长，最终落至滚筒底部或者是颗粒堆积层的上方.随着筒体的转动，丝状颗粒与高温壁面不断发生碰撞接触，从而使得颗粒的总体温度逐渐上升.

图6(a)为不同筒壁温度条件下滚筒中丝状颗粒温度标准偏差随时间的变化.由图中可以看出，在干燥的初始阶段，颗粒间温度的不均匀性迅速增大，但随着干燥的进行，颗粒之间的温度差别又呈现出逐渐缩小的趋势.这是由于颗粒的热量大部分是通过与高温壁面接触导热过程中获得的，在干燥的初始阶段，固相堆积层外侧的颗粒由于紧靠筒壁或抄板，因此温度上升的速度较快，而堆积体内部的颗粒只能从颗粒间的接触导热以及与空气的对流换热中获取相对较少的热量，所以温度上升的速度较慢，颗粒彼此间的温度差别也就迅速拉大.此后，随着物料不断被抄起和撒落，每个颗粒与高温壁面在单位时间内接触的次数逐渐趋于一致，使得颗粒从外界获得的热量大体相当，因此颗粒间的温度差别逐渐减小.

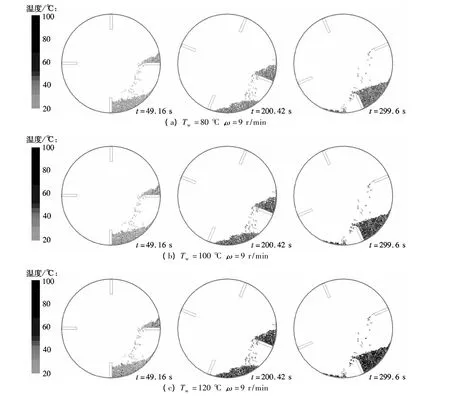
图5 不同筒壁温度条件下颗粒温度分布的变化过程

图6 丝状颗粒温度和含水率标准偏差随时间的变化

图6(b)为不同筒壁温度条件下，丝状颗粒含水率标准偏差随时间的变化，与温度标准偏差呈现的趋势有相似之处，在干燥的初始阶段，颗粒间含水率的不均匀性迅速增大，之后开始减缓.这是由于初始阶段，少部分处于堆积体外侧的颗粒获取大量的热量，因此这部分颗粒的含水率会迅速下降;而另一方面，大部分处于堆积体内部的颗粒由于获取的热量较少，颗粒温度上升缓慢，因此水分气化量很小甚至为零［19］.这就造成了高温与低温颗粒含水率彼此间的差别迅速拉大.随着颗粒温度不断提高，颗粒总体进入等速干燥阶段，但是由于原先的高温颗粒仍处于等速阶段，在干燥介质的气速、温度等外部干燥条件恒定的情况下，这部分颗粒含水率下降的速度不变.因此在预热段之后，虽然颗粒含水率的差别仍旧逐渐增大，但增大的趋势开始放缓.

从图6(b)还可看出，含水率标准偏差并没有像温度标准偏差那样，到一定干燥时间点后出现逐渐减小的情况.这是因为本文所涉及的工况中热风的流速很小，因而物料的传质速率较小，在干燥时间为300 s时，颗粒间的干燥程度仍未达到一定的均匀性，反而出现含水率偏差逐渐拉大的趋势.然而，通过加大气体流速，可以观察到含水率标准偏差首先不断增大，之后又逐渐缩小的趋势，如图7所示.并且气速越大，含水率标准偏差开始降低时所对应的干燥时间点越靠前.这说明对于滚筒横向传热传质过程，只要满足一定的干燥条件(热风流速等)或一定的干燥时间，筒体内部丝状颗粒的干燥程度将会越来越均匀.

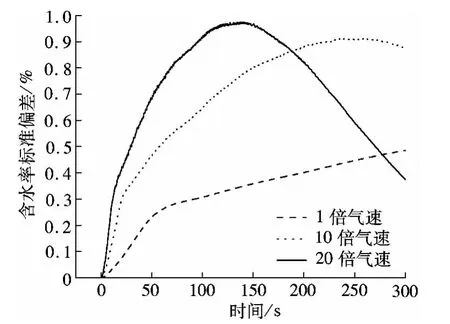
图7 不同气速条件下丝状颗粒含水率标准偏差的变化

从定量层面了解丝状颗粒在滚筒中各种传热量的相对贡献，能够为寻求滚筒干燥设备的合理状态控制参数提供依据，为此本文将针对不同工况条件下的传热模式进行对比.模拟过程中时刻跟踪每个颗粒，在每个时间步长内计算出每个颗粒的各种换热量，并在模拟完成后对数据进行统计分析.图8为滚筒转速9 r/min、热风温度100℃时，不同筒壁温度下各类传热模式的相对贡献率.从图中可以看出，丝状颗粒在滚筒中所获取的热量主要来自于与高温壁面之间的接触导热，3种不同工况下颗粒的接触导热量占总体换热量的比例都在90%以上，并且随着筒壁温度的升高，其所占的比例进一步增大.从图中还可看出，颗粒从筒体获取的热量要大于从抄板获取的热量，这是由于筒体的面积要大于抄板的面积，在同一干燥时间段内，颗粒群与筒体总的接触时间要大于与抄板接触的时间.

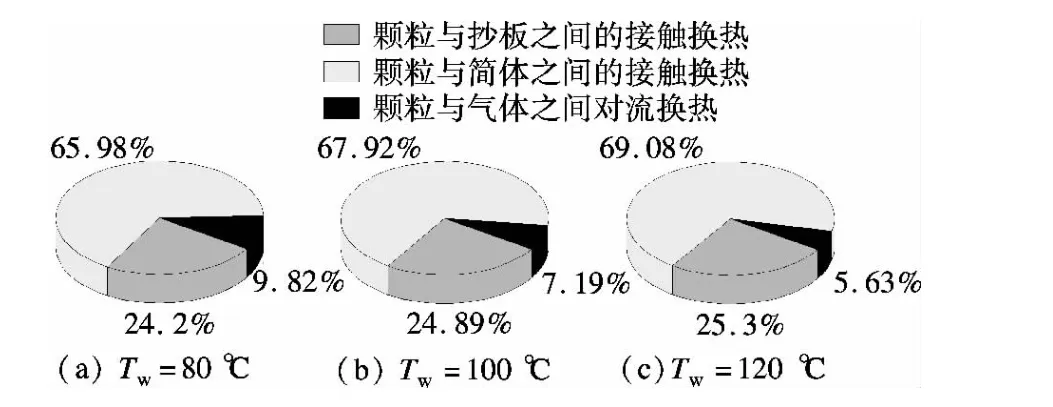
图8 不同筒壁温度条件下各类传热模式的相对贡献率

为研究抄板布置方式对其中丝状颗粒传热传质特性的影响，下面将分别针对升举式抄板和均布式抄板滚筒进行相关研究.如图9所示，为使这2种抄板的换热面积一致，将均布式抄板滚筒筒体中部的4块抄板设为绝热边壁条件.

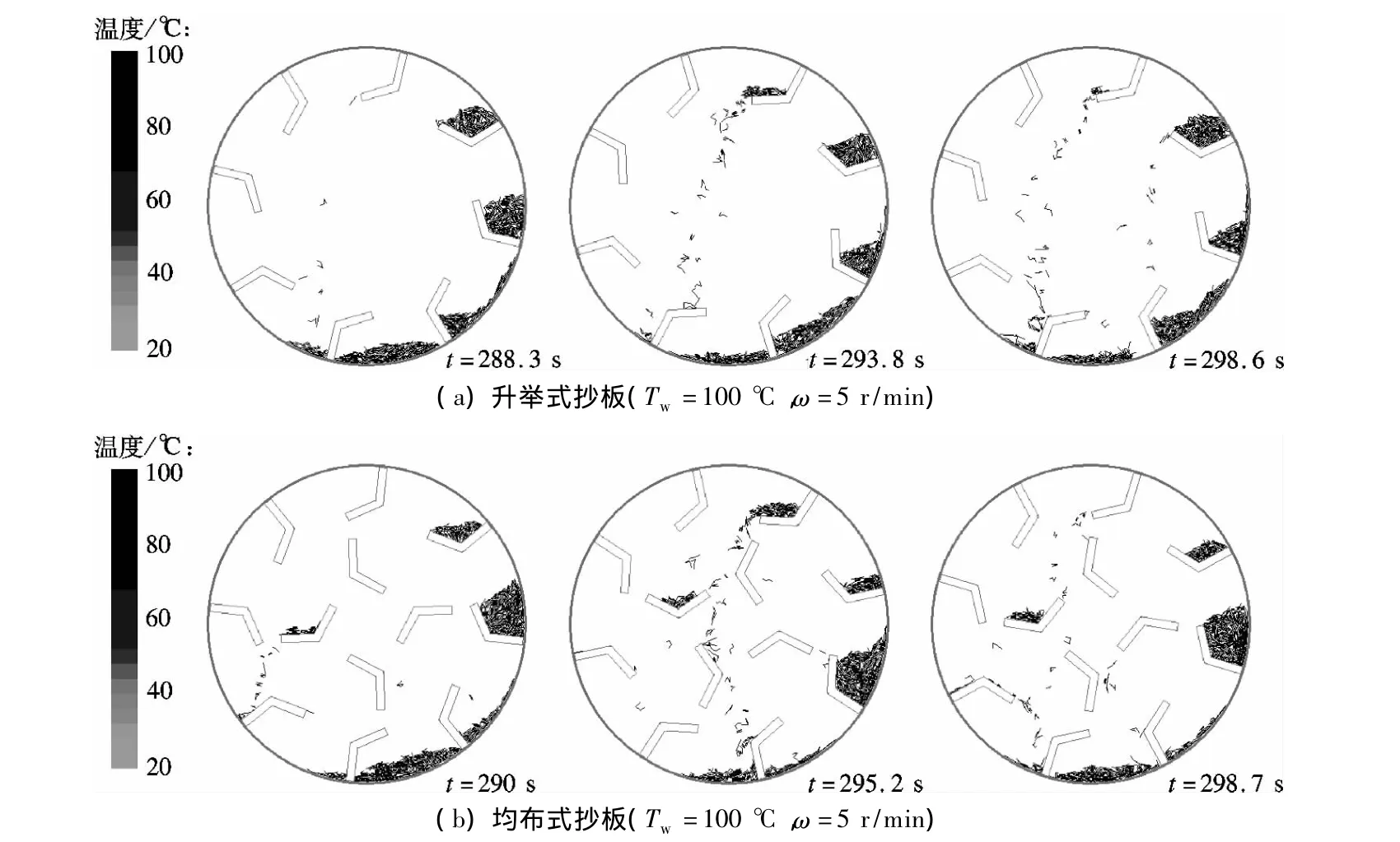
图9 不同抄板布置方式条件下丝状颗粒在滚筒内的瞬时分布状态

图10为筒壁温度100℃、滚筒转速5 r/min和气流温度100℃条件下，升举式抄板和均布式抄板丝状颗粒温度和含水率随时间变化的模拟结果.可以看出，抄板布置为升举式时，颗粒温度上升速度比均布式的略大，而含水率降低的速度则是均布式的略大.这一方面是因为均布式抄板滚筒旋转时，会有部分颗粒散落在筒体中部的绝热抄板上(见图9(b))，因而缩短了颗粒与高温壁面之间的总体接触时间，所获取的接触传热量因此相对较低，温度上升的速度也就相对缓慢.由图9(a)和(b)两组图的对比可见，在均布式抄板情况下，由于颗粒与筒体中部4块抄板的碰撞改变了丝状物料的飘落轨迹，使得撒落颗粒所形成的料幕要更为均匀和连续，因此颗粒与气流之间接触更充分，其对流传质量也就更大.并且筒体内抄板与抄板之间所堆积的颗粒数量大多情况下相对较少，颗粒可以更为均匀地分布在滚筒的横截面上，这从生产的角度来说，更有利于物料与干燥气流之间的对流传质和传热.所以在相同时间内，均布式抄板滚筒所能够气化的水分要比升举式的多.

图11(a)、(b)统计了不同抄板形状的颗粒温度和含水率标准偏差随时间的变化.从图中可以看出，当抄板为均布式时，滚筒中丝状颗粒温度和含水率标准偏差的数值都相对较小，这是因为在该抄板条件下，颗粒在横截面上的分布更为均匀，因而每个颗粒与筒壁或抄板接触的概率更加趋于一致，这就使得颗粒所获取接触导热量更加均匀，颗粒彼此间的温度和含水率随之也更加均匀.

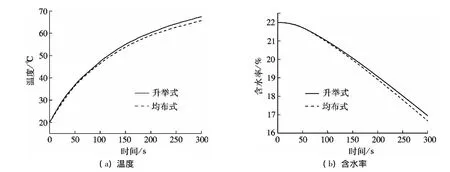
图10 不同抄板布置条件下颗粒温度和含水率的变化

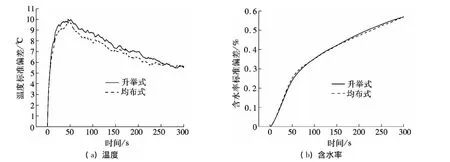
图11 不同抄板布置时颗粒温度和含水率标准偏差的变化

4 结论

1)筒壁温度是滚筒设备的重要操作参数之一，对滚筒横向截面内颗粒的传热传质特性有着直接且重要的影响.随着滚筒筒壁温度的升高，颗粒平均温度上升以及含水率下降的速度明显加快.

2)根据滚筒中丝状颗粒温度标准偏差随时间变化的模拟结果可以看出，在干燥的初始阶段，颗粒彼此间温度的不均匀性迅速增大，但随着干燥的进行，颗粒之间的温度差别又呈现出逐渐缩小的趋势.另一方面，颗粒间含水率的不均匀性在干燥的初始阶段迅速增大，但只要满足一定的干燥条件或一定的干燥时间，筒体内部丝状颗粒的干燥程度将会越来越均匀.

3)丝状颗粒在滚筒中所获取的热量主要来自于与高温壁面特别是与筒体之间的接触导热，并且随着筒壁温度的升高，接触导热量所占总体换热的比例进一步增大.

4)抄板布置为升举式时，颗粒温度上升速度比均布式的略大，而含水率降低的速度则相反.均布式抄板的颗粒在滚筒横截面上的分布及颗粒间的温度和含水率更加均匀.

References)

［1］Kamke F A，Wilson J B.Computer simulation of a rotary dryer.Part1:retention time ［J］.AIChE Journal，1986，32(2):263-268.

［2］Pkez-Correa J R，Cubillos F，Zavala E，et al.Dynamic simulation and control of direct rotary dryers［J］.Food Control，1998，9(4):195-203.

［3］黄志刚.转筒干燥器中颗粒物料流动和传热传质过程的研究［D］.北京:中国农业大学工学院，2004.

［4］常剑，高金森，徐春明.气固两相流中颗粒间碰撞传热进展［J］.计算机与应用化学，2007，24(4):425-428.Chang Jian，Gao Jinsen，Xu Chunming.Advances of impact heat transfer between particles in gas-solid flow［J］.Computers and Applied Chemistry，2007，24(4):425-428.(in Chinese)

［5］Chaudhuri B，Muzzio F J，Tomassone M S.Modeling of heat transfer in granular flow in rotating vessels［J］.Chemical Engineering Science，2006，61(19):6348-6360.

［6］Chaudhuri B，Muzzio F J，Tomassone M S.Experimentally validated computations of heat transfer in granular materials in rotary calciners［J］.Powder Technology，2010，198(1):6-15.

［7］Shi D，Vargas W L，Mccarthy J J.Heat transfer in rotary kilns with interstitial gases［J］.Chemical Engineering Science，2008，63(18):4506-4516.

［8］Geng Fan，Li Yiming，Wang Xinyong，et al.Simulation of dynamic processes on flexible filamentous particles in the transverse section of a rotary dryer and its comparison with ideo-imaging experiments［J］.Powder Technology，2011，207(1/2/3):175-182.

［9］Tsuji Y，Kawaguchi T，Tanaka T.Discrete particle simulation of two-dimensional fluidized bed［J］.Powder Technology，1993，77(1):79-87.

［10］Fraige F Y，Langston P A，Chen G Z.Distinct element modelling of cubic particle packing and flow［J］.Powder Technology，2008，186(3):224-240.

［11］Hilton J E，Mason L R，Cleary P W.Dynamics of gas-solid fluidised beds with non-spherical particle geometry［J］.Chemical Engineering Science，2010，65(5):1584-1596.

［12］Anthony Wachs.A DEM-DLM/FD method for direct numerical simulation of particulate flows:sedimentation of polygonal isometric particles in a Newtonian fluid with collisions［J］.Computers ＆Fluids，2009，38(8):1608-1628.

［13］Yagi S，Kunii D.Studies on effective thermal conductivities in packed beds［J］.AIChE Journal，1957，3(3):373-381.

［14］朱立平，袁竹林，闫亚明，等.基于离散单元法的丝状颗粒传热数学模型［J］.化工学报，2012，63(7):2051-2058.Zhu Liping，Yuan Zhulin，Yan Yaming，et al.Model of heat transfer in filamentous granular materials based on discrete element method［J］.Journal of Chemical Industry Engineering，2012，63(7):2051-2058.(in Chinese)

［15］Wakao N，Kaguei S.Heat and mass transfer in packed beds McGraw-Hill［M］.New York:Gordon and Breach Science Publishers，1997:135-158.

［16］Guardo A，Coussirat M，Recasens F，et al.CFD studies on particle-to-fluid mass and heat transfer in packed beds free convection effects in supercritical fluids［J］.Chemical Engineering Journal，2007，62(18/19/20):5503-5511.

［17］Ranz W E.Friction and transfer coefficients for single particles and packed beds［J］.Chem Eng Prog，1952，48(4):247-253.

［18］Incropera F P，de Witt D P，Bergman T L，et al.Fundamental of heat and mass transfer［M］.6th ed.New York:John Wiley＆ Sons，2007:233-324.

［19］潘永康，王喜忠.现代干燥技术［M］.2版.北京:化学工业出版社，2007:12-14.