非自治Gilpin-Ayala收获系统的优化控制策略
2014-06-27郭海叶窦家维
郭海叶, 窦家维
(陕西师范大学 数学与信息科学学院, 陕西 西安 710062)
0 引言
众所周知, 人类过度开发是造成资源枯竭危机的重要原因, 可再生资源优化管理问题的研究直接关系到资源的可持续发展. 如何利用有限的可再生资源, 实现其可持续开发和利用, 己成为经济管理学家及生态学家们普遍关注的重要问题. 在文献[1,2]中, 作者对可再生资源优化管理的基本理论和方法进行了系统的阐述. 文献[3-13]讨论了各类可再生资源的优化控制问题, 其中文献[3-7]研究Logistic模型的连续收获及脉冲收获问题. 本文主要研究Gilpin-Ayala模型描述的种群系统的优化控制问题.
本文所研究的模型由下面的系统描述:
x′(t)=r(t)x(t)-m(t)xθ+1(t)-h(t)
(1)
其中r=r(t)表示种群的内禀增长率,θ>0为常数,m(t)>0,m(t)xθ+1(t)项描述种群生长的密度制约因素.h(t)≥0表示收获函数, 当h(t)≡0时, (1)式表示Gilpin-Ayala增长模型,注意到,当θ=1时,(1)为古典的Logistic增长模型,已有很多文献对其进行了研究.Gilpin-Ayala模型是Logistic模型的推广,更加符合实际,研究也更加困难.文献[14]研究了随机Gilpin-Ayala竞争模型的稳定性,文献[15]研究了具有时滞的Gilpin-Ayala系统概周期解的存在性, 文献[16]对于自治的Gilpin-Ayala模型系统的最优开发问题进行了研究. 关于系统(1)的优化控制问题的研究结果还不多.本文主要对非自治Gilpin-Ayala模型在几种收获情形下的优化控制策略进行研究,研究结果推广、改进了文献[16]及关于Logistic模型的一些相关结论.
1 周期Gilpin-Ayala系统的优化收获策略
本部分主要研究关于Gilpin-Ayala收获系统的周期优化控制问题.这时,系统表示为
x′(t)=r(t)x(t)-m(t)xθ+1(t)-E(t)x(t)
(2)
其中r(t),m(t)为连续可微的τ-周期函数,E(t)≥0表示收获努力量,假设E(t)为分段连续的τ-周期函数.
1.1 周期解的存在性和稳定性
关于系统(2),首先研究其周期解的存在性和稳定性.
定理1记
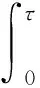
则有下面结论:
(i)当R≤0时, 系统(2)的任一具有正初值的解, 当t→∞时趋向于0;
(ii)当R>0时, 系统(2)存在唯一的全局渐近稳定的正周期解.
证明:(i) 直接求解(2), 得到
(3)
由(3)可知, 当R≤0,且x(0)>0时, 有
因此, 对于所有具有正初值的解x(t),当t→∞时,x(t)→0,即种群趋于灭绝.
(ii)对系统(2)作变换, 令x=z-1/θ,得到非齐次线性方程
z′(t)=-θ[r(t)-E(t)]z(t)+θm(t)
(4)
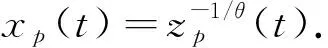
设x(t)为系统(2)的任意一个给定的具有正初值的解, 则z(t)=x-θ(t)为(4)的解. 由于
则有
由于(4)的解zp(t)是全局渐近稳定的, 根据上式可知(2)的正周期解xp(t)也是全局渐近稳定的.证毕.
1.2 最优收获策略
下面讨论系统(2)的最优收获问题. 选取E(t)为控制变量,其允许集为由满足下面条件的函数E(t)构成的集合G:E(t)为分段连续的τ-周期非负函数, 且E(t)的取值应使系统(2)具有全局渐近稳定的正周期解, 即要求E(t)满足
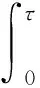
(5)
控制目标是要求在一个周期内的总收获量最大, 即目标泛函设为
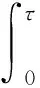
(6)
其中x(t)为系统(2)对应于E(t)的唯一正周期解, 即有
x(0)=x(τ)
(7)
如果存在E*(t)∈G, 使得
(8)
则称E*(t)是一个最优收获策略, 而对应的周期解x*(t)称为最优轨线.
下面将利用极值原理求解优化控制问题(2), (6)~(8).
首先建立Hamilton函数为
H(x,E,λ,t)=E(t)x(t)+λ(t)·
[r(t)x(t)-m(t)xθ+1(t)-E(t)x(t)]
其中λ=λ(t)为协态变量.由极值原理知,如果E=E*(t)是一个最优策略,x=x*(t)为对应的最优轨线, 则一定存在协态变量λ(t), 满足
(9)
并且E=E*(t)要使得H(x,E,λ,t)取得最大值. 令
得到λ=1, 将其代入(9)式得到
(10)
进一步将x(t)将代入(2)式得到
(11)
因此, 我们得到下面定理.
定理2如果下面条件
满足,则优化控制问题(2),(6)~(8)存在最优解. 其中最优控制策略E*(t)和最优轨线x*(t)分别由(11)及(10)给出. 这时, 一个周期内的最优收获量为
证明:由系统(2)右端函数的性质及解关于初值及参数的连续依赖性可知优化解一定存在,而定理的条件保证了E*(t)∈G,又由于(11)及(10)给出的E*(t)、x*(t)是满足极值原理的唯一解,因此其为最优解. 将其代入(6)式,即可得到最优收获量J(E*(t))的表达式.
定理1和定理2对文献[16]的主要结论进行了推广.
1.3 自治Gilpin-Ayala系统的最优持续收获策略
作为周期系统的一个特殊情形, 考虑下面的自治Gilpin-Ayala收获模型:
x′(t)=rx(t)-mxθ+1(t)-h(t)
(12)
其中r,m为正常数.
如果以收获函数h(t)作为控制变量, 以系统能获取最大的持续产量为管理目标, 则由定理2 容易证明下面结论.
定理3如果r2m>(θ+1)/θ2成立, 对于系统(12), 最优控制函数, 即最优收获率h(t)为:
证明:在模型(12)中, 令h(t)=E(t)x(t),则(12)成为(2)的形式. 故由定理2, 这时最优解为:
E(t)=EMSY=rθ/(θ+1)
x(t)=xMSY=(r/m(θ+1))1/θ
进一步, 对于任意给定的时间区间[0,τ], 在该区间内各点处由上面最优解所确定的收获率, 即最优收获率为:
证毕.
我们注意到, 对于自治的Gilpin-Ayala系统(12), 将其作为周期系统(2)的特殊情形考虑(即h(t)=E(t)x(t))时,所得到的最优控制策略E(t)=EMSY及对应的最优轨线x(t)=xMSY均为常函数,这时,周期解x(t)=xMSY是系统的平衡解.当θ=1,m=r/K时, 定理3的结论推广了[1,2]中关于Logistic模型的一些相关结果.
2 非自治Gilpin-Ayala系统的最大收获量问题
本部分考虑一类非自治的Gilpin-Ayala收获系统的优化控制问题.
在t∈[0,τ]内考虑下面初值问题:
(13)
假设r≥0,m(t)>0,是连续可微函数,收获函数h(t)≥0分段连续. 优化控制问题是:选择控制变量h(t),使得在[0,τ]内, 由下式给出的总收获量最大:
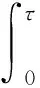
(14)
使得J(h(t))能取得最大值的收获函数h=hM(t)及系统(13)相应的解x=xM(t)称为最优解.
从下面的求解过程中可获得控制问题的最优解及最大收获量的具体表达式.
首先, 在t∈[0,τ]内假设下面条件成立:
(15)
由于在t∈[0,τ]内, 种群增长率为
g(x)=r(t)x(t)-m(t)xθ+1(t)
为使J(h(t))最大, 显然应该在每个时刻t∈[0,τ],保证g(x)尽量大.为此,对每个t∈[0,τ], 令
g′(x)=r(t)-(θ+1)m(t)xθ(t)=0
可得到
(16)
由于
g″(x)=-θ(θ+1)m(t)xθ-1(t)<0
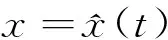
(17)
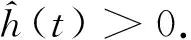
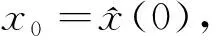
这时, 最大收获量为
这时, 最大收获量为
x′(t)=r(t)x(t)-m(t)xθ+1(t),x(0)=x0
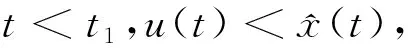
hM(t)=0,xM(t)=u(t),0≤t 这时对应的最大收获量为 如果不存在满足上面性质的t1, 则对于所有的t∈[0,τ],选取 hM(t)=0,xM(t)=u(t) 为最优解, 这时最大收获量为 YM=u(τ) x′(t)= (3+0.1sin(πt))x(t)- 0.85x3(t)-E(t)x(t) (18) 假设目标泛函为 (19) 由于在t∈[0,2]上, 定理2的条件满足. 则由定理2可知, 使得目标泛函(19)取得最大值的最优轨线, 最优策略和一个周期内的最优收获量分别为: x′(t)=0.8x(t)-(t+1)x5(t)-h(t) (20) 假设目标泛函为 (21) 由于当t∈[0,1]时, (i)当x0=0.632 5时, 最大收获量为 0.468 6+0.531 8=1.000 4 (ii)当x0=1时, 最大收获量为 1.000 4+1-0.632 5=1.367 9 0.287 0+0.531 8=0.818 8 因此, 该种情形下, 最大收获量为 YM=u(1)=0.612 5 本文研究了几类非自治的Gilpin-Ayala收获系统的最优控制策略.首先利用微分系统的极值原理获得了周期收获系统的优化控制策略,在定理2的条件成立时获得了最优控制策略及可持续的最优收获量的具体表达式.其次研究了一类在给定时间区间内,需要根据具体的初值条件确定其最大收获量的收获策略控制问题.我们以保证该时间区间内各点处的增长率最大为基础,在各种初值情况下分别获得了最优解和最大收获量的具体表达式.由于本文所研究的模型比较广泛,所用的研究方法和所获得的结论对于资源管理者制定优化管理决策提供了理论依据, 具有重要的实际意义. [1]Clark C W.Mathematical bioeconomics:the optimal management of renewale resources[M].New York:Wiley,1990. [2]陈兰荪,孟新柱,焦建军.生物动力学[M].北京:科学出版社,2009. [3]Cookel K L,Witten M.One-dimensional linear and logistic harvesting models[J].Math.Model,1986,7(2-3):301-340. [4]Gao S J,Chen L S,Sun L H.Optimal pulse fishing policy in stage-structured models with birth pulses[J].Chaos Solutions Fractals,2005,25(5):1 209-1 219. [5]Tang S Y,R A Cheke,Xiao Y N.Optimal impulsive harvesting on non-autonomous Beverton-holt difference equations[J].Nonlinear Anal:Theory Methods,2006,65(12):2 311-2 341. [6]Xu C L,Mark S,Boyce D,et al.Harvesting in seasonal environments[J].Math.Biol,2005,50:663-682. [7]Zhang X Y,Shuai Z S,Wang K.Optimal impulsive harvesting policy for single population[J].Nonlinear Anal:Real World Appl,2003,4(4):639-651. [8]Zhang Y J,Xiu Z L,Chen L S.Optimal impulsive harvesting of a single species with Gompertz law of growth[J].Biol.Syst,2006,14(2):303-314. [9]Elena Braverman,Reneeta Mamdani.Continuous versus pulse harvesting for population models in constant and variable environment[J].Math.Biol,2008(57):413-434. [10]鲁红英,王 克.自治单种群模型及其最优捕获策略[J].系统科学与数学,2004,24(2):200-205. [11]王战平,赵 春.一类周期种群系统的稳定性分析及最优控制问题[J].生物数学学报,2008,23(2):225-230. [12]Dong L Z,Chen L S,Sun L H.Optimal harvesting policies for periodic Gompertz systems[J].Nonlinear Anal:Real World Appl,2007,8(2):572-578. [13]王丽敏,谭远顺.周期Gompertz生态系统中的最优脉冲控制收获策略[J].系统科学与数学,2007,27(4):520-528. [14]Lian B S,Hu S G,Wang H C.Stability of stochastic Gilpin-Ayala competition models[J].Math.Appl,2007,20(2):408-414. [15]胡 猛,王 健.一类时滞Gilpin-Ayala系统的概周期解的存在性[J].兰州理工大学学报,2013,39(1):142-146. [16]张晓颖,李晚霞.单种群生物资源的最优开发[J].长春大学学报,2001,11(6):20-22.3 应用举例
3.1 考虑由下面模型描述的周期Gilpin-Ayala收获系统(设周期τ=2)
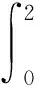
3.2 考虑由下面模型描述的非自治Gilpin-Ayala收获系统(设τ=1)
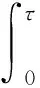
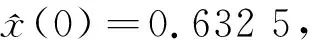
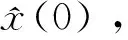
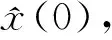
4 结论
