非等间距GM(1,1)模型背景值的构造及其应用

杨跃东， 冯倩妮

(1.上海师范大学 数理学院, 上海 200234； 2.华东理工大学 理学院, 上海 200237)

0 引言

非等间距GM(1，1)模型的预测精度，取决于参数列Q，而Q中具体参数a和b的取值，则依赖于背景值z(1)(tm)的构造形式.所以，背景值序列z(1)(t)的构造，成为影响非等间距GM(1，1)模型普适性和预测精度的关键因素之一.

已有大量文献对背景值构造问题进行了研究，并提出了一些改进方法[1-7].文献[8]给出了用一次累加生成序列(1-AGO)x(1)(t)与x轴在有限区间[m,m+1]围成实际面积作为背景值的构造方法;文献[9]提出了一种非等间距GM(1，1)模型背景值的构造方法.该方法主要思想是用指数函数来对一次累加生成序列(1-AGO)进行拟合;文献[10]给出了通过积分来重新构造GM(1,1)模型背景值的方法，同时证明了该构造方法所得背景值更接近于真实值;文献[11]的主要思想是用背景值代替中心值，将一次累加生成序列(1-AGO)进行开方运算，进而得到新序列,然后将中心值与背景值替换，最终得到基于中心化的非等间距模型,取得了较高的预测精度.

本文尝试使用Lagrange插值多项式，对一次累加生成序列(1-AGO)进行拟合，进而利用该函数估计出一个更为精准的背景值.同时,还在理论上证明了该方法的有效性.并且将该方法应用于人工降雨中不同时间播撒碘化银时的降雹量的建模中，该应用结果证明了本文所提出方法是有效的.

1 非等间距GM(1,1)模型背景值的改进

1.1 非等间距GM(1,1)模型的建模步骤

定义1设非负递增序列x(0)={x(0)(t1),x(0)(t2),…,x(0)(tn)}，若间距tm=tm-tm-1≠const，则称x(0)为非等间距序列.

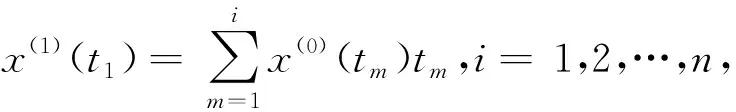
定义3设非负递增序列z(1)(t)={z(1)(t2),z(1)(t3),…,z(1)(tn)},其中z(1)(tm)=0.5x(1)(tm)+0.5x(1)(tm-1)为一次累加生成序列(1-AGO)的均值生成序列.

对一次累加生成序列(1-AGO)x(1)建立非等间距GM(1，1)模型，对应的微分方程为：

(1)

其差分形式(灰色微分方程)为：

x(0)(tm)+az(1)(tm)=b

(2)

在式(2)中：z(1)(tm)为x(1)(tm)在相应区间[tm-1,tm]上的背景值，而定义3中序列z(1)(t)称为一次累加生成序列(1-AGO)的背景值序列.

将式(2)改为矩阵形式为：

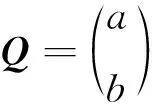
(3)

若规定x(1)(t1)=x(0)(t1),则灰色微分方程式(2)的时间响应函数(离散解)：

m=1,2,…,n

还原得到拟合后的数据为：

x(0)(tm) =x(1)(tm)-x(1)(tm-1)

(4)

1.2 背景值的改进

本文用Lagrange插值多项式，对一次累加生成序列(1-AGO)进行拟合，进而利用该函数估计出一个更为精准的背景值.

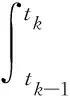
btk

(5)

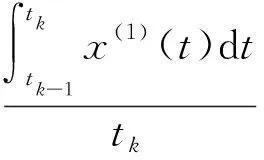
初始给定的背景值z(1)(tm)=0.5x(1)(tm)+0.5x(1)(tm-1)，最终的实质是梯形面积近似代替积分值，是一个平滑公式.当数据随时间变化较为平缓时，估计偏差不大，但当数据随时间急剧增长时，直接利用梯形面积来代替积分值显然具有较大偏差，且在一定程度上会影响非等间距灰色模型的适用范围.

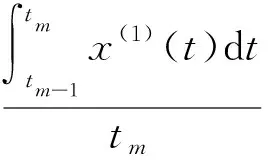
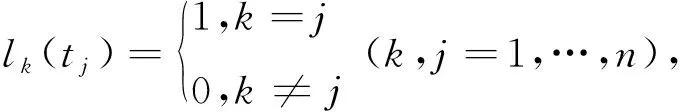
对应n个时间节点t1,t2,…,tn，其Lagrange插值多项式的n-1次插值基函数为：

由式(4～5)可得，其n-1次插值多项式为：

(6)

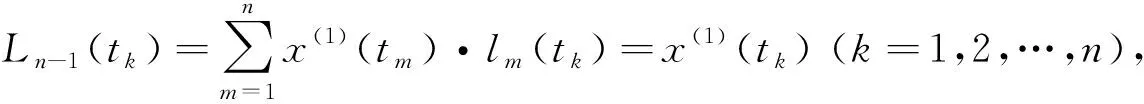
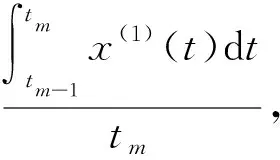
(7)

将式(7)代入式(3)，得到经背景值修正后的时间响应函数(离散解)为：

2 应用实例

人工影响天气系统，是防灾减灾的重要措施之一，可在水资源的合理利用和防御减轻气象灾害等中发挥重要作用.它主要是运用云形成和降水发生的物理学原理，通过向云中播撒催化剂的方法，使局部地区天气过程朝着有利方向发展的一种科学措施，能够实现防雹、消雾、消雨等目的.因此，建立GM(1,1)模型研究人工影响天气中不同时间播撒碘化银时的降雹量的变化趋势具有十分重要的意义.

现通过传统非等间距GM(1,1)模型和本文提出的经背景值改进的非等间距GM(1,1)模型,对不同时间播撒碘化银时的降雹量(数据见表1所示)进行建模，并将这两种不同模型的拟合精度加以比较，结果见表1所示.

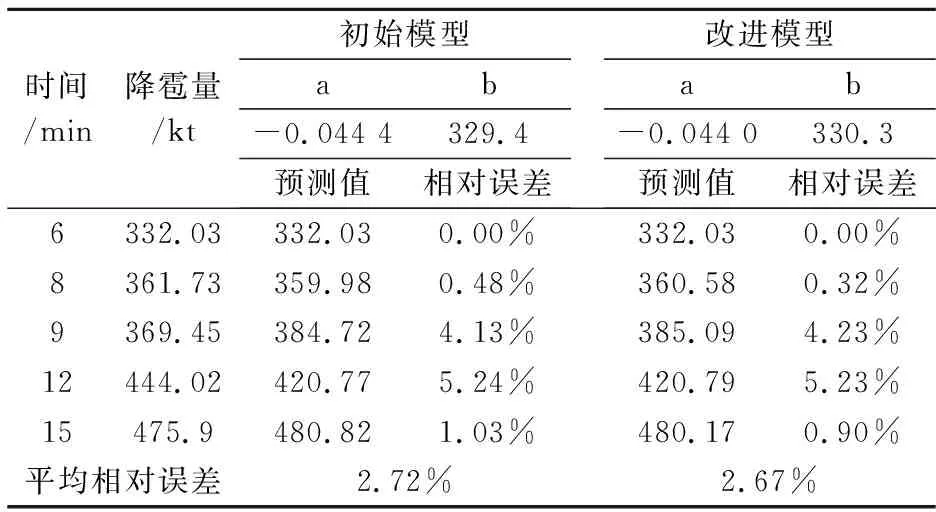
表1 不同模型拟合结果和相对误差比较[12]

从表1我们可以看出，通过应用本文所提出的经背景值改进的非等间距GM(1,1)模型拟合精度高于传统的非等间距GM(1,1)模型，其平均相对误差为2.67%，而传统非等间距GM(1,1)模型的平均相对误差为2.72%.可见，改进模型结果可以更好地反应降雹量随着碘化银播撒剂量改变时的真实值.

3 结束语

基于背景值的构造理论，本文提出了一种提高非等间距GM(1,1)模型数据拟合精度的方法，并且在理论上给出了新背景值构造的推理过程.同时还应用实例运算结果证明，本文所提出的经背景值改进的非等间距GM(1,1)模型的拟合精度要高于传统的非等间距GM(1,1)模型.这为研究在人工影响天气系统中，如何控制催化剂播撒量来达到理想的防雹、消雾、消雨等目的，在方法上提供了一些参考.

[1]陈有亮．非等距时序灰色预测方法及其在岩石力学与工程中的应用[J].系统工程理论与实践，2003,23(11)：130-134．

[2]王寒梅，唐益群，严学新，等.软土地区工程性地面沉降预测的非等时距GM(1，1)模型[J].工程地质学报，2006，14(3)：398-400．

[3]谭冠军．GM(1，1)模型的背景值构造方法和应用(I)[J].系统工程理论与实践，2000,20(4)：98-103．

[4]李翠凤，戴文战．非等间距GM(1，1)模型背景值构造方法及应用[J].清华大学学报，2007，47(S2)：1 730-1 731．

[5]罗 党，刘思峰，党耀国．灰色模型GM(1，1)优化[J].中国工程科学，2003,5(8)：50-53．

[6]刘圣宝,张公让,李巧巧,等.非等间距GM(1,1)模型背景值的改进及其最优化[J].合肥工业大学学报，2010,33(11)：1 749-1 751.

[7]刘 乐，王洪国，王宝伟．基于背景值构造方法的GM(1，1)模型优化[J].统计与决策，2009(1)：153-155．

[8]刘思峰,郭天榜,党耀国,等.灰色系统理论及应用[M].北京：科学出版社,1999．

[9]Fengxao Wang．Improvement on unequal interval gray forecast model[J].Fuzzy Information and Engineering，2006，6(1)：119-122．

[10]戴文战，李俊峰．非等间距GM(1，1)模型建模研究[J].系统工程理论与实践，2005，25(9)：89-93．

[11]王丰效，郭天印．基于中心逼近的非等距灰色模型[J].陕西理工学院学报，2007，23(2)：79-80．

[12]张 蔷.人工影响天气试验研究和应用[M]．北京：气象出版社，2011:216.