基于有限元的压电双晶片驱动模拟分析

张昌松， 雷春耀， 高 峰

(1.陕西科技大学 机电工程学院， 陕西 西安 710021； 2.西北工业大学 材料科学与工程学院， 陕西 西安 710068)

0 引言

压电双晶片广泛应用于驱动和感应领域，是开发MEMS(微电子机械系统)的关键元件，非常适合做微尺度高频运动[1,2].随着微电子机械系统的发展，压电双晶片越来越多地被用来作为微执行器和传感器器件，如旋转精密驱动器、仿生飞行器、微型压电泵、飞机增稳驱动[3-8]等.在设计这些执行器时，常常需要考虑执行器的机电转换特性以及驱动特性，用数学物理方法计算压电双晶片自由端的挠度、转角等[9,10].自由端位移量的大小即挠度是衡量压电双晶片驱动特性的一个重要指标，也是压电双晶片类制动器的一个重要参数.

ANSYS软件是一款集结构、热、流体、电磁场、声场分析与一体的大型通用有限元分析软件，具有多物理场耦合功能，压电分析是结构场和电场的耦合，这为分析压电双晶片的动态特性提供了更好的选择.然而，ANSYS软件分析只是模拟分析，分析的结果与理论结果是存在偏差的，如果不考虑这些偏差的影响，将影响执行器件的精度.本文使用数学物理方法和ANSYS12.0软件分析了在不同长厚比值K下和不同电压载荷下的0～3型压电复合物双晶片的变形情况，并比较了模拟分析的结果和理论计算结果的差距，分析了二者存在的相对偏差以及偏差存在的原因.

1 压电双晶片的驱动机理

压电双晶片由两个连在一起极性相反的压电层组成，其间以导电胶粘接，构成一端夹持、另一端自由的悬臂梁形式[11-13]，如图1所示.

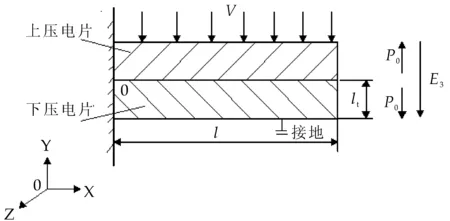
图1 压电双晶片结构简图

压电双晶片的振动模式为横场长度伸缩振动.当外加电场为E3时，由于压电材料的逆压电效应，压电陶瓷片将沿其长度方向(图示x方向)产生形变S1，在y，z方向不产生形变，既S1=0，S2=0，S3=0.由于上压电片的极化方向P0与外加电场E3方向相反，而下压电片的极化方向P0与外加电场E3方向相同，由压电振子的振动模式可知，上压电片将产生伸长变形，下压电片产生收缩变形，同时由于中间采用导电胶连接，最终造成压电双晶片整体产生向下弯曲变形.当对压电双晶片施加交变电场时，因组成双晶片的两片晶片极化方向相反, 双晶片将做与外加激励信号同频的弯曲振动[14].

压电双晶片符合弹性力学的五个基本假设条件，根据压电本构方程、电学理论和弹性理论可得到在恒定电场下，梁的变形位移方程如下[15].

压电双晶片的近似挠度曲线方程：

(1)

压电双晶片自由端，x=l处的位移量：

(2)

令K=l/lt，为单层压电材料的长度和厚度的比值，则式(2)可化为：

y|x=l=0.375d31K2V

(3)

式中，d31为压电应变系数；V为施加于上压电片的电压；l为压电片的长度；lt为压电片的厚度.

从式(3)可以看出，压电双晶片自由端的位移量与压电材料、器件形状以及加载的电压有关系.当压电材料(d31)和形状(K)一定时，压电双晶片的自由端位移量的大小与加载的电压V成正比关系；当材料和加载的电压一定时，压电双晶片的自由端位移量的大小与长厚比K成抛物线的关系.

2 利用ANSYS直接耦合场分析

利用ANSYS 12.0软件的直接耦合场进行分析.对双晶片的驱动分析采用稳态分析，选用稀疏矩阵(SPARSE)求解器.其中l=0.1 m，lt=0.000 5 m，V=100 V，选取耦合单元中的PLANE 13单元类型，KEYOPT(1)=7，0～3型压电复合材料的其它属性如表1所示.

表1 材料的基本属性

2.1 建立有限元模型

定义工作文件名和工作标题，选取单元类型PLANE 13，单元自由度选取“UX UY VOLT”，依照表1定义材料性能参数.建立两个局部笛卡尔坐标系11、12，原点皆为(0，0，0)，其中12相对于11在z轴方向上旋转180 °，并激活坐标系11.建立两个面模型，面A1，A2信息如表2所示.

表2 面信息表

单击“ANSYS Main Menu→Preprocessor→Modeling→Operate→Booleans→Glue→Areas”命令，打开Glue Areas对话框，单击Pick All按钮关闭该对话框.

设置网格划分的尺寸长度为0.000 5.使用映射网格划分(Mapped)方法，在局部坐标系11中划分面A1，在局部坐标系12中划分面A3，划分网格后的图形如图2所示(自由端).

图2 生成的网格模型

2.2 设置边界条件

在x=0边界节点上施加约束，约束自由度为“UX UY”，在y=0.000 5的边界节点上施加电压为100伏特的电压，y=-0.000 5的边界接地，如图3所示.

2.3 驱动模拟求解，后处理

查看模型位移场分布等值线图，如图2所示.从图4可以看到，当V=100 伏特，l=0.1 m时，自由端的位移量为0.329×10-4m.

图3 加载电压约束图

图4 位移场分布等值线图

3 结果与分析

3.1 电压V变化

随着电压的变化，自由端的位移量有限元分析结果δ和理论计算结果σ如表3所示.

表3 自由端位移量随电压V变化情况表(l=100)

注：分析结果(×10-4)保留小数点后三位，单位米/m，电压单位伏特/V.

有限元分析结果和理论计算结果用图5表示为：

图5 分析结果以及局部放大图

从表3和图5可以看出，有限元分析的结果和理论计算的结果相差不大，ANSYS分析的结果与电压的关系曲线和理论计算曲线几乎吻合.当压电双晶片的材料(d31)和尺寸(K)一定时，对于自由端位移量大小的变化，ANSYS分析的结果与电压近似为正比关系，这和理论计算一致.

分析表3和图5中的数据可知，当电压小于40伏特时，有限元分析的结果和理论计算的结果是一致的，当超过40伏特时，二者开始出现偏差，最大的偏差率为0.5%，且出现在60伏特附近.

3.2 长厚比K值变化

随着K值的变化，压电双晶片自由端位移量有限元分析结果δ和理论结果σ如表4所示.

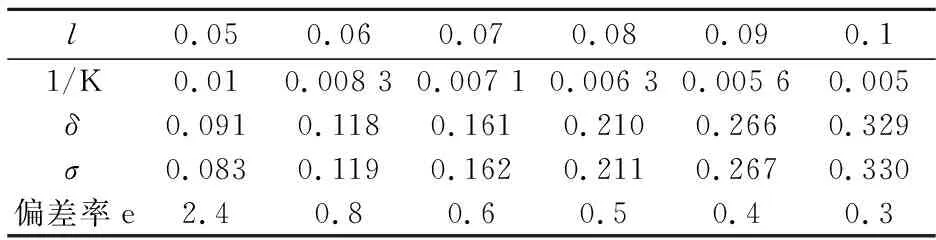
表4 自由端位移量随比值K变化情况表(v=100)

注：分析结果(×10-4)保留小数点后三位，单位米/m.

两种结果如下图所示：

图6 分析结果以及局部放大图

由表4和图6可以看出，两种方法分析的结果也是吻合，随着K值的变化，两者的偏差率也在变化.当K值较小时，有限元ANSYS软件分析的结果与理论相差比较大，随着K值的增大，偏差越来越小.

3.3 数据分析

利用数学物理方法和有限元法计算在不同长厚比值K和不同外载条件下的压电双晶片自由端位移量的大小，通过对比两种方法的结果数据，我们可以看出：

(1)有限元分析的结果和数学物理方法分析的结果表明，当压电材料(d31)一定的情况下，自由端位移量的大小与所加外载(电压V)为正比关系，与材料的长度和厚度的比值K成抛物线的关系.

(2)两种方法分析的结果具有一致性，但也存在一定的偏差，当电压变化时，最大偏差率为0.5%，当比值K变化时，最大偏差率为2.4%.

通过对两种方法对比分析，影响这种情况的原因有：

(1)模型的建立.建立的数学模型和有限元模型都忽略了压电双晶片中间导电层的影响，简化了模型，把压电陶瓷假设为弹性体，将压电层元件等效为一个Euler-Bernoulli梁，所以二者分析的结果近乎一致.

(2)网格划分的影响.当分析的有限元模型一定，在网格划分的大小也一致的情况下，所受外载(电压V)的增大可能会使分析的结果出现一定的偏差.

(3)在进行有限元耦合分析时，采用的是小变形分析，结构场中采用的是线性理论，当长厚比值K较小的时候，会使分析结果的偏差加大，增大长厚比K，分析结果的偏差率会降低.

(4)分析所用计算机以及软件精度的影响.

3.4 结果讨论

通过分析两种方法下的自由端位移量的数据与长厚比值K和外载电压的关系，可以得到：

(1)在测量准确度误差允许的范围内，可以用压电双晶片自由端的ANSYS分析的结果代替理论计算，在测量要求比较高的系统中，可以提前考虑偏差，用相对偏差来对ANSYS分析的结果进行修正.

(2)在压电材料的耐压范围内，当增大器件的长度可以增大自由端的位移量，增大器件的测量范围，同时增大测量的精度.

(3)当压电双晶片模型一致的情况下，在分析比较大的外载(电压)情况下，适当增大分析的网格密度，可以增加有限元分析的精度.

4 结论

本文用数学物理方法和有限元方法分析了压电双晶片的自由端在不同情况下的位移量，并比较分析了二者之间存在的相对偏差.分析结果显示二者具有一致性，但也存在一定的偏差，当电压变化时，最大偏差率为0.5%，当比值K变化时，最大偏差率为2.4%.这为利用有限元ANSYS软件精确分析压电双晶片类的制动器提供了依据.

[1] Kursu O,Kruusing A,Pudas M,et al.Piezoelectric bimorph charge mode force sensor[J].Sensors and Actuators A:Physical,2009,153(1):42-49.

[2] 张 斌,陈西平,浮红霞,等.压电双晶片作为驱动的精密定位机构研究[J].机械与电子,2009,200(6):39-41.

[3] 张宏壮,曾 平,华顺明,等.压电双晶片型惯性冲击式旋转精密驱动器研究[J].光学精密工程,2005,13(3):298-304.

[4] 张宏壮, 程光明, 曾 平,等.压电双晶片型2自由度精密驱动器的动态特性[J].机械工程学报,2007,43(2):87-91.

[5] 王姝歆,陈国平,周建华,等.压电双晶片驱动的仿生柔性扑翼机构研究[J].光学精密工程,2006,14(4):617-622.

[6] 杨树臣,程光明,刘国君,等.微型压电泵系统的设计研究[J].光学精密工程,2005,13(3):318-323.

[7] 王海宁,崔大付,耿照新,等.压电双晶片驱动的压电微泵的研究[J].压电与声光,2007,29(3):302-304.

[8] 张晓丽,王晓洁,梁大开,等.基于压电双晶片的微型无人机增稳驱动系统研究[J].传感器与微系统,2011,30(1):35-37.

[9] Smits J G,Ballato A.Dynamic admittance matrix of piezoelectric cantilever bimorphs[J].Journal of Mi-croelectromechanical Systems,1994,3(3):105-112.

[10] Smits J G,Choi W S,Ballato A.Resonance and antiresonance of symmetric and asymmetric cantilev-ered piezoelectric flexors[J].Ultrasonics,Ferroelec-trics and Frequency Control,IEEE Transactions on,1997,44(2):250-258.

[11] 党沙沙,许 洋,张红松,等.ANSYS 12.0多物理耦合场有限元分析从入门到精通[M].北京：机械工业出版社,2010:154-155.

[12] 董兴建,孟 光.压电悬臂梁的动力学建模与主动控制[J].振动与冲击,2005,24(6):54-56.

[13] 王 涛,秦 荣,李双蓓.压电智能简支梁力电耦合性能分析[J].材料科学与工程学报,2007,25(6):961-964.

[14] 叶会英,禹延光,姬建伟,等.压电双晶片动态机电耦合特性分析[J].压电与声光,2002,24(5):411-414.

[15] 李龙土,邬军飞,褚祥诚,等.压电双晶片的有限元分析及实验[J].光学精密工程,2008,16(12):2 378-2 383.