基于小波变换新阈值函数的地震资料去噪方法

郭 思，郭 科，陈 聆，侯锐锋

（1.成都理工大学数学地质四川省重点实验室，成都 610059；2.中国石油川庆地质勘探开发研究院，成都 610051）

基于小波变换新阈值函数的地震资料去噪方法

郭 思1，2，郭 科1，陈 聆1，侯锐锋1

（1.成都理工大学数学地质四川省重点实验室，成都 610059；2.中国石油川庆地质勘探开发研究院，成都 610051）

探讨在地震勘探中小波变换处理非平稳信号的时频分析方法，从强噪声地震信号中除去干扰进而提取有效信号。在D.L.Dohono提出的小波阈值去噪方法的基础上，提出了一种新的阈值函数用于非平稳强震降噪。该函数是介于硬、软阈值函数之间的一个可调函数，具有计算稳定性好、精度高、收敛速度快、对模型参数α的选择简单易于操作等特征。通过仿真实验和实际地震处理验证，表明所构造的新阈值函数能有效改善地震剖面处理效果，达到提高信噪比的目的。

小波变换；地震资料；随机噪声；阈值函数

除去地震资料的噪声，提高其中信号的可靠性，一直是地球物理工作者所追求的目标。由于随机噪声无法寻求统一的时间规律，频带较宽，无法确定视速度以及传播方向，因此随机噪声的去除为提高信噪比的一个关键点。为了能有效地除去随机噪声，人们提出了各种各样的去噪方法，其中以近年来兴起的小波变换方法效果为佳。小波变换理论是20世纪80年代中后期发展起来的［1］，它能将地震信号进行多尺度分解。

由于有效信号和随机噪声在不同小波分解尺度上有着不同的特征，如：有效信号出现的短暂时刻内，小波系数将出现瞬时模极大值，且随分解尺度递增，而有效信号的随机噪声的小波系数极大值和稠密度将随此分解尺度的增大而减小［2，3］。小波变换去噪方法正是利用有效信号和随机噪声的这一截然相反的特性来进行信噪分离。

1995年，D.L.Donoho提出的小波阈值去噪方法［4］，由于它易于实现，计算速度快，而在众多小波去噪方法中成为最广泛应用的一种。但小波阈值去噪方法中常用的软、硬阈值方法均存在一些缺陷，如：硬阈值方法处理的重构系数在阈值点处出现间断，重构信号易出现Pseudo-Gibbo现象；而软阈值处理的重构系数虽然整体连续性好，但重构系数与分解系数间总存在着恒定的偏差［5］。这些都影响着小波阈值去噪的效果。本文给出一种新的阈值函数，该函数不仅易于计算，而且具有优越的数学特性和清晰的物理意义，通过仿真实验和实际应用构建的新阈值函数效果明显。

1 阈值函数的一种改进方案

假设有如下观测信号

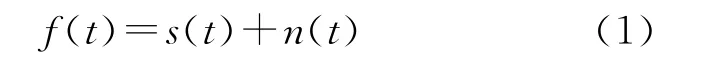
其中：f（t）为含噪的随机信号；s（t）为原信号；n（t）服从高斯白噪声分布，即N（0，σ2）分布。对于一维随机信号f（t）来说，首先将其进行离散化采样处理，得到N点离散信号f（n），（n＝0，1，2，…，N－1），其小波变换为

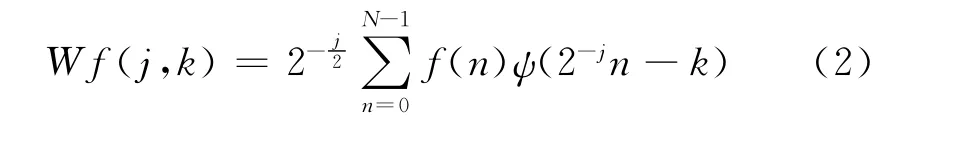
（2）式中Wf（j，k）为小波系数。为简化运算将小波系数Wf（j，k）简记为Wj，k，对含噪随机信号f（t）＝s（t）＋n（t）作离散小波变换。由于小波变换属线性变换，故得到的小波系数Wj，k仍由两部分组成，一部分是有效信号s（t）对应的小波系数，记为Uj，k；另一部分是噪声n（t）对应的小波系数，记为Vj，k。

D.L.Donoho提出的基于最小均方误差（MSE）的小波阈值去噪方法已经取得了广泛的应用，该方法的基本流程如图1［5］。

图1 小波阈值去噪流程图Fig.1 The flow of de-noising by wavelet threshold

而传统的加权平均方法，一般是把加权因子μ的大小简单设为常数0.5。而该设定的常数μ在一定程度上克服软、硬阈值法的缺点，但仍然存在缺陷：首先阈值函数仍然为不连续函数，其次小波系数的估计值与原值仍然存在固定偏差，只是偏差＜0.5。为了更好地发挥加权平均阈值估计方法的优点，本文给出一种新的加权因子计算式

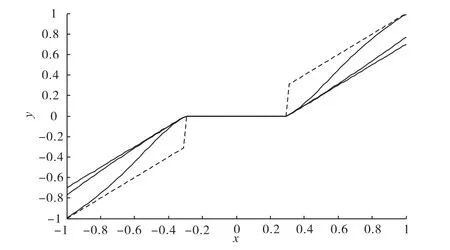
图2 新阈值函数Fig.2 The new threshold function

2 仿真与对比

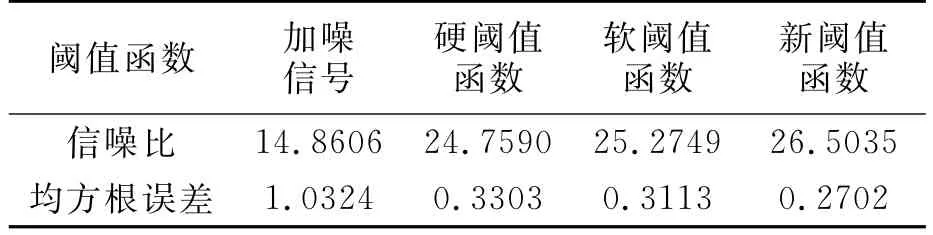
表1 各种方法的信噪比和均方误差Table 1 The signal to noise ratios and mean square errors by various methods

3 应用效果

3.1 合成地震记录去噪

本节将前面的新阈值函数去噪方法用于合成地震记录。假设地层水平，且为均匀介质构成，子波均采用Ricker子波，反射深度为100 m；反射层上、下速度分别为2 km／s，3 km／s；最小偏移距（震源到第一个检波器的距离）为10 m；道数为100；记录的长度为600 s。

图4为合成地震记录的新阈值函数去噪结果，（A）为原始的合成地震记录，（B）为含有随机噪声的人工合成地震记录，（C）为用新阈值方法去噪的合成记录。通过（C）与（A）的对比可以看出新阈值方法在合成地震记录去噪中达到了好的效果。

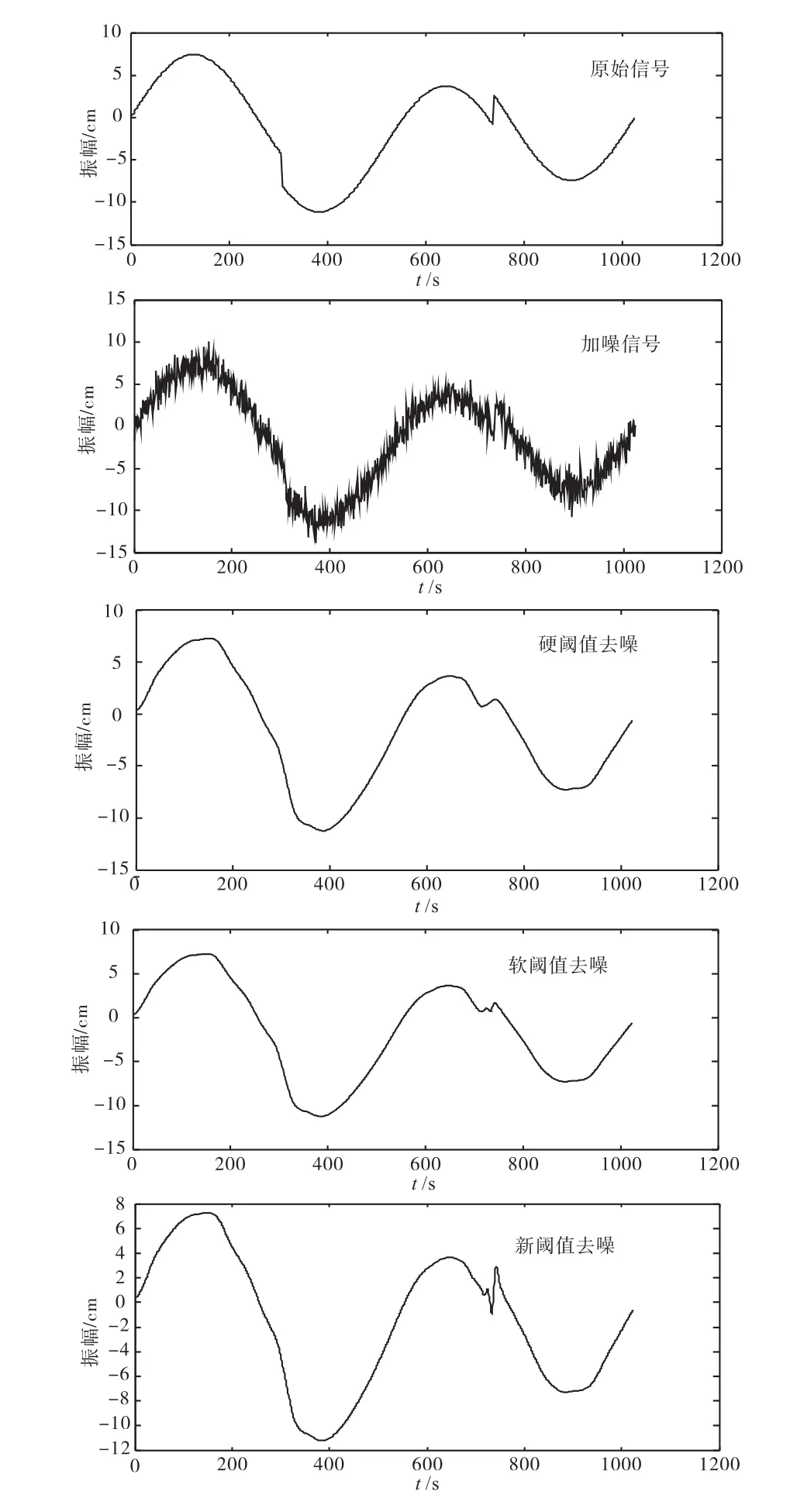
图3 不同阈值函数去噪效果图Fig.3 The effect diagram of de-noising by different threshold functions

3.2 实际地震资料去噪

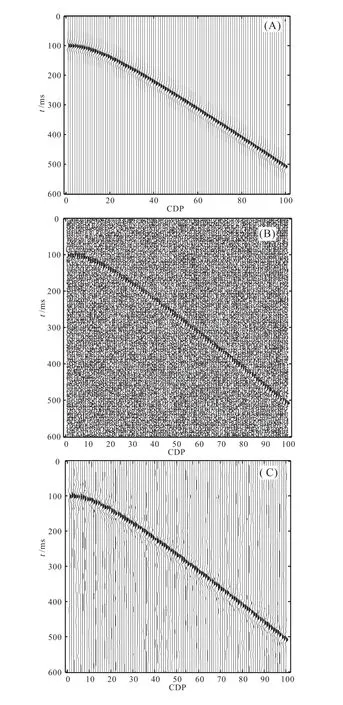
图4 合成地震记录去噪Fig.4 De-noising by synthetic seismograms

为说明本文提出的去噪方法的有效性，我们选取了某工区的一小块实际地震数据剖面图来进行试验。在图5所示的剖面图中，共提取了100道地震数据，每道的采样点数为450个，采样间隔为2 ms。其中，（A）为含随机噪声的实际地震资料，（B）为用新阈值方法去噪的合成记录。通过两幅图的对比，可以看出经过新阈值方法处理后的地震数据噪声明显减少，分辨率也有了提高。因此，该方法对地震数据的去噪有一定的效果。

4 结论

本文在D.L.Dohono提出的小波阈值去噪

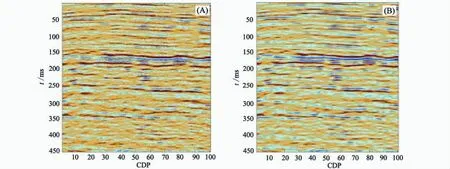
图5 实际地震记录去噪Fig.5 De-noising by actual seismic records

方法的基础上，提出了一种新的阈值函数，该阈值函数能够使小波变换阈值去噪方法的优越性得到充分发挥，与传统的硬阈值和软阈值函数相比，该函数不仅易于计算，而且具有优越的数学特性和清晰的物理意义。将该方法用于实际地震资料的去噪，结果表明该方法能够有效地除去原始地震数据中的随机噪声，并提高了地震资料信噪比。

［1］李建平.小波分析与信号处理——理论、应用及软件实现［M］.重庆：重庆出版社，1997：5－8.

Li J P.Wavelet Analysis and Signal Processing：Theory，Applications and Software［M］.Chongqing：Chongqing Publishing，1997：5－8.（In Chinese）

［2］Mallat S G A.Theory from multiresolution signal decomposition：The wavelet representation［J］.IEEE Trans PAM I，1989，11：674－693.

［3］Mallat S.Getal singularity detection and processing with wavelets［J］.IEEE Trans on Information Theory，1992，38（2）：617－643.

［4］Donoho D.De-noising by soft-thresholding［J］.IEEE Trans on IT，1995，3：613－627.

［5］刘涛，曾祥利，曾军.实用小波分析入门［M］.北京：国防工业出版社，2006：116－117.

Liu T，Zeng X L，Zeng J.Getting Practical Wavelet Analysis［M］.Beijing：National Defense Industry Press，2006：116－117.（In Chinese）

［6］彭军.传感器与检测技术［M］.西安：西安电子科技大学出版社，2003：231－242.

Peng J.Sensors and Detection Technology［M］.Xi'an：Xi'an University of Electronic Science and Technology Press，2003：231－242.（In Chinese）

［7］程正兴.小波分析算法与应用［M］.西安：西安交通大学出版社，1998：114－122.

Cheng Z X.Wavelet Analysis Algorithms and Applications［M］.Xi'an：Xi'an Jiaotong University Press，1998：114－122.（In Chinese）

Seismic data de-noising method based on a new threshold function of wavelet transformation

GUO Si1，2，GUO Ke1，CHEN Ling1，HOU Rui-feng1
1.Geomathematics Key Laboratory of Sichuan Province，Chengdu University of Technology，Chengdu 610059，China；
2.CNPCChuanqing Drilling Engineering Company Limited，Chengdu 610051，China

In seismic exploration，how to remove the interference from the seismic signal with strong background noises and extract the effective signal is the key of the seismic data processing.Wavelet transform is a time-frequency analysis to process non-stationary signals.Based on the wavelet threshold de-noising method proposed by D.L.Dohono，a new threshold function used in the nonstationary earthquake reduction noise is presented.This function is an adjustable function between hard and soft threshold functions and has the good stability of computation，high precision，fast convergence speed.Its choice of model parameters is simple and easy to operate.The simulation results and the actual seismic data processing show that the new constructed threshold function can effectively improve the seismic data processing，in order to increase the signal to noise ratio.

wavelet transform；seismic data；random noise；threshold function

P631.4

A

10.3969／j.issn.1671-9727.2014.03.14

1671-9727（2014）03-0378-04

2013-11-07

国家自然科学基金资助项目（41272363）

郭思（1987－），女，硕士，工程师，研究方向：油气地球物理勘探，E-mail：guosi123456＠126.com。