中国象棋属于EXPTIME-complete问题

高强，徐心和

(东北大学信息科学与工程学院，沈阳 110004)

中国象棋属于EXPTIME-complete问题

高强，徐心和

(东北大学信息科学与工程学院，沈阳 110004)

寻找棋类游戏的理想解是计算机博弈研究的目标，而计算复杂性是不可逾越的障碍。首先介绍了计算复杂性类中的EXPTIME-complete问题及它的一个实例——G3游戏。构建了一个n×n中国象棋的归约模型，模型由6部分组成，分别为布尔控制器、开关、子句通道与文字通道的交叉区域、兑子区域、延迟区域及九宫。在该模型上模拟进行G3游戏，并最终证明了G3游戏可多项式时间内归约到n×n的中国象棋，从而证明了n×n的中国象棋属于EXPTIME-complete问题。

计算机博弈;中国象棋;计算复杂性;指数时间的完全问题;归约

计算机博弈是让计算机给出着法，能够下棋，属于人工智能学科极具挑战性的研究领域。计算机博弈的最高境界是找到该棋种的理想解，即不败解。而计算机博弈的最大困难和无法逾越的障碍是求解问题过程中的计算复杂性。通过对问题的计算复杂性进行分类可以了解该问题被求解的难易程度，如果问题被证明是难解的(例如NP-complete、PSPACE-complete及EXPTIME-complete)，则不必将大量的精力花费在寻找问题的解析解上，而只能去寻求某种近似解。国外有很多学者在研究计算机博弈问题的计算复杂性，国际象棋［1］和西洋跳棋［2］被证明属于EXPTIME-complete问题。这2个棋种的计算复杂性证明在构建模型的过程中，都用到了一个已被证明为EXPTIME-complete的G3游戏［3］。围棋被证明属于PSPACE-hard问题［4］(围棋也被怀疑属于EXPTIME-complete问题［1］)，五子棋［5］、六子棋［6］、奥赛罗棋［7］被证明属于PSPACE-complete问题。这些棋种的计算复杂性证明都用到了广义地理学游戏(generalized geography game)［8］。亚马逊被证明属于PSPACE-complete问题［9］，在证明过程中，它采用了一种公式博弈(formula game［8］)方法。

中国象棋是一种历史悠久的棋类游戏。在兵种及走法方面，它与国际象棋有许多相似之处。9 ×10的中国象棋与8×8的国际象棋在状态空间复杂度、博弈树复杂度方面的比较见表1［10］。

表1 中国象棋与国际象棋的复杂度比较(数据以10为底)

由表1可见:中国象棋的复杂度与国际象棋的复杂度相当，既然n×n的国际象棋已被证明属于EXPTIME-complete问题，所以有理由推测n×n的中国象棋也应属于EXPTIME-complete问题。

本文在第1节分析了EXPTIME-complete问题及它的一个典型实例——G3游戏。根据计算复杂性类中完全问题的定义［1］，首先在第2节证明了n×n的中国象棋属于EXPTIME问题，然后在第3节重点构建了一个n×n中国象棋的归约模型，并在此模型上模拟进行G3游戏，证明了G3游戏可在多项式时间内归约到n×n中国象棋，从而证明了n×n中国象棋属于EXPTIME-complete问题。为了保证论述的严密性，第4节给出了归约模型中不恰当走法的分析。第5节对于此证明的完全性给出了论证。

1 EXPTIME-complete问题

EXPTIME问题的定义该复杂性类是一些确定型问题的集合，这些问题可以使用确定型图灵机在O(2p(n))的时间内解决，这里的p(n)代表n的某个多项式。属于该复杂性的问题，它的难度不小于P，NP，NP-complete以及空间复杂性类(PSPACE和PSPACE-complete)［11］。而EXPTIME-complete问题是EXPTIME复杂性类中最难的问题，其定义可参考其他复杂性类完全问题的定义［1］，如下:

一个问题B属于EXPTIME-complete，如果它满足2个条件:

1)B属于EXPTIME;

2)每个属于EXPTIME的问题在多项式时间内可以归约到B。

常见的属于EXPTIME-complete问题的有停机问题［8］、简洁电路问题［11］、G3游戏等。

该游戏中的每个局面(position)是一个4元组(τ，R-LOSE(X，Y)，B-LOSE(X，Y)，α)，其中τ∈{R，B}，它表示当前走棋方，R-LOSE=C11∨C12∨C13∨…∨C1p和B-LOSE=C21∨C22∨C23∨…∨C2q是属于12DNF的布尔公式，其中每个C1i(1≤i≤p)和C2j(1≤j≤q)是最多12个文字之间的与运算，每个文字是集合X(Y)中的一个变量。例如:z 或¯z(变量z的非运算);α是对X∪Y的一个赋值，如X={x1，x2，x3}，Y={y1，y2，y3}，则X∪Y= {x1，x2，x3，y1，y2，y3}。对X∪Y赋值，就是对该集合中的各个元素赋值为0或1。比赛双方交替进行，R方或B方通过改变集合X和Y中的一个变量的值进行走棋。更精确地，R方能够从局面(R，R-LOSE(X，Y)，B-LOSE(X，Y)，α)下棋到局面(B，R-LOSE(X，Y)，B-LOSE(X，Y)，α')，当且仅当α与α'不同，并且在α的赋值下，R-LOSE(X，Y)的布尔值为false。如果在R(B)走了若干步后，公式R-LOSE(B-LOSE)值为true，那么R(B)失败。在文献［3］中，该游戏被证明属于EXPTIME-complete问题。此游戏的规则与许多棋类游戏有类似之处。比如，在游戏中有2个参与方，通过判断布尔公式R-LOSE(B-LOSE)的值是否为真来判断某方是否输棋(也就是说，这2个布尔公式可以看作是棋类游戏中的估值函数)。4元组中的α就是双方兵力的集合，从α对应的4元组到α'对应的4元组可以看作是棋类游戏中的一个走法。因此，选用G3游戏来构造机器博弈问题的归约模型是非常合适的。

2 对于中国象棋计算复杂性的证明

本文的主要工作是证明对于任意的一个n×n的中国象棋局面，判定黑方(红方)是否能够获胜的问题属于EXPTIME-complete。根据计算复杂性类complete问题的定义［1］，证明广义化的中国象棋属于EXPTIME-complete的步骤如下:

1)证明广义化的中国象棋属于EXPTIME;

2)构造一个归约模型，使得G3游戏可归约到中国象棋;

3)证明此归约可在多项式时间内完成。

2.1 中国象棋的广义化

对于固定棋盘规模的博弈问题(如9×10的中国象棋或8×8的国际象棋)，可能出现的局面数是有穷的，即产生的局面数是一个常量。而研究问题的计算复杂性时采用的是渐近法，用此方法来度量复杂性随着问题规模的增加而变化的增长率。因此，需要将问题的规模广义化，即规模是任意大的［8］。对于中国象棋的广义化，要保证各个棋子的走法不变，双方的帅(将)只能有1个，不能广义化为多个，帅(将)和士不能出“九宫”(由于棋盘被广义化，所以原来九宫的规模也被扩大了)。

2.2 n×n的中国象棋属于EXPTIME问题

该证明比较简单，可以进行粗略计算。假设计算机处理象棋的一个局面需要一个单位时间，则n×n的中国象棋可能产生的局面总和就是其被求解所需总时间的上限值。中国象棋的双方兵种之和为14，则n×n个交叉点的中国象棋所能产生的局面总数上限为15n×n。由此得证，n×n的中国象棋属于EXPTIME问题。

3 归约模型的构建

本文给出一个n×n的中国象棋局面(实例)，并在此局面上模拟进行任意一个G3游戏。所构建的归约模型(即局面)遵循的主要思想是:在该模型上能够模拟进行G3游戏，并对G3游戏所包含的变量适当地赋值，确保它们所在的子句为true，进而使得G3游戏在n×n中国象棋棋盘上能够被求解;双方都采用车作为进攻的棋子，在走棋过程中，将出现吃子和兑子的情况，最终通过计算吃掉对方的帅(将)所需的总的步数判定哪一方需要的步数更少，那么该走棋方先于对方获胜。也就是说，在这个构建的局面上，G3游戏中的某个走棋方存在一种赢棋策略，当且仅当中国象棋的某个走棋方在此给定的局面中存在一种赢棋策略。

3.1 归约模型中各构件的说明

为了在n×n中国象棋的归约模型上模拟G3游戏，构建此模型的过程中，既要考虑G3游戏的特点，也不能违反中国象棋的走棋规则。本文所构建的归约模型主要包括布尔控制器、开关、子句通道、兑子区域、延迟区域和九宫，这6个构件组成了一个n×n中国象棋的特定局面。

3.1.1 布尔控制器

一个布尔控制器(boolean controller，BC)的作用是实现对G3游戏的4元组中的一个布尔变量赋值(true或false)。图1显示了红方布尔控制器(red boolean controller，RBC)的基本结构，其中包含的棋子有红兵、红相、红车、红马、红炮、黑车;包含文字(与G3游戏的子句所包含的文字对应)通道即x通道和～x通道，以及一个红方的时钟通道(red clock channel)。只要将该图旋转180°，并将各个位置上的棋子由红兵换成黑卒、红相换成黑相、红车换成黑车、红马换成黑马、红炮换成黑炮、黑车换成红车等，就能得到Black Boolean controller(BBC)的结构。在一个布尔控制器中，只有1个红相和2个车(一个红方、一个黑方)可以主动走棋，其他棋子处于僵局状态，不能主动走棋，但根据各个棋子的走法规则，它们可以被动地吃子。由这些棋子构成的区域迫使双方的车经由给定的通道离开布尔控制器，在Red Boolean controller中，若黑方的车吃掉了红方的棋子，则它将立即被邻近的红方棋子吃掉，从而使红方可以经由正常的通道离开布尔控制器，并最终获胜;若有一方的车不经由正常通道离开布尔控制器(例如，黑方的车第一步没有直接走到x通道或～x通道的横向虚线处，而是只走了一格)，那么对方的车同样可经由正常的通道离开布尔控制器，并最终可能先于对方获胜。这种不恰当的走法将在后面章节详细论述。

开始时，红方的相必须先走出一步，它只有2个走法(即图中的2个虚线位置)，这2个走法决定了黑方的车是从x通道还是～x通道离开布尔控制器。若红相移动到南方(即下方)的虚线位置，则黑车可从x通道离开，说明该布尔控制器对变量x赋值为true;相反，若红相移动到北方(即上方)的虚线位置，则黑车从～x通道离开，说明该布尔控制器对变量x赋值为false。如前所述，红相走一步，然后黑车走一步到达x通道或～x通道的横向虚线处;接下来轮到红方的车走棋，它可以从东北角的x通道或～x通道离开，也可以从北方的Red clock channel(时钟通道)离开此布尔控制器。

图1 红方的布尔控制器

3.1.2 开关(switch)

开关的作用是确保只有一个对方的车能到达子句通道，并确保对方的车无法从子句通道再进入BC。图2显示了开关的基本结构。同样，由红马、红兵、红相和红炮组成的区域是一个僵局，它们不能主动移动，但根据各个棋子的走法规则，它们可以吃对方的棋子。

当有黑方的车从RBC到达开关时，黑车将按照红方棋子形成的通道走棋，途中将吃掉拦在通道上的一个红马，然后安全地离开开关，到达子句通道。如果黑方的车在吃掉红马后，打算反向走棋并返回布尔控制器，此时被吃掉的红马的东南方的红相将走棋到西北角处，这样红相原来位置左侧的若干个红方的炮(此处炮的数量大于或等于G3游戏所包含的变量的总数)将封锁住红相右侧的通道，使得黑方的车无法返回布尔控制器。同样，子句通道中的黑车也无法经由开关返回布尔控制器。

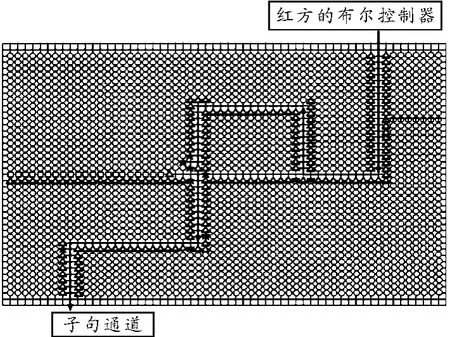
图2 红方的开关

3.1.3 子句通道(C1i-channels)

子句通道对应G3游戏中布尔公式R-LOSE (B-LOSE)所包含的子句C1i或C2j。根据G3游戏的定义，每个子句包含若干个文字，这些文字的“与”运算的值就是该子句的运算结果。图3显示了各个子句通道与各个文字通道形成的交叉结构。

如上所述，黑方的车从RBC经由开关到达子句通道，只有子句包含的文字的值为真(如x)时，黑车才可以停在对应的值为真的文字通道(x通道)与该子句通道的交叉点处，并经由此子句通道到达兑子区域(exchanging chess zone);否则黑车无法停在文字通道与子句通道的交叉点处，如图3所示。假设子句C11不包含¯x，如果黑车经由¯x通道停在此文字通道与C11通道的交叉点处，此时黑车将被西南方的红马吃掉，从而无法安全到达兑子区域(exchanging chess zone)，最终红方将获胜。此处的一些不恰当走法将在后面章节详细论述。

假设某个子句包含的变量总数为p，如该子句通道与文字通道的交叉点处安全地停有p个黑方的车，则这p个黑车向东移动至兑子区域。

图3 子句通道与文字通道的交叉结构

3.1.4 兑子区域

如果某个子句通道上停有与该子句所包含的文字数相同的黑方的车，则这些车经由该子句通道到达兑子区域。如图4所示，在兑子区域的通道上有一个红方的马，该棋子受到正上方若干个红炮的保护，因此双方开始兑子，直到最后一个红方的炮被黑车吃掉。其中红炮的个数为p-x，p为该子句所包含的文字数，x为奇数且1≤x＜p。剩下的黑方的车安全地到达九宫(nine-palace)。

图4 兑子区域

3.1.5 九宫和延迟区域

九宫和延迟区域(delay zone)是归约模型中的最后2个构件。在中国象棋中，九宫是帅(将)和士活动的区域，也是最后一道防线。对于n×n的中国象棋，该区域的帅(将)仍然只有一个，士的数量为多个，士只能在九宫中活动，它的走法为斜走斜吃，且每次只能走一格。图5显示了九宫的基本结构(图中未显示帅的位置)，若干个黑方的车到达九宫，将与九宫中的士进行兑子，并最终吃掉红方的帅。此处子句通道连接的九宫共有2× (x-1)个士。

延迟区域与Clock channel相连接，如图6所示，是一列马，马的数量为12k-5。其中，k为G3游戏对应的4元组中子句包含的最大文字数，即1≤k≤12。车吃掉若干个马之后，可直接吃掉对方的帅(将)。

图5 九宫

图6 延迟区域

每个构件中，由若干个棋子构成的区域，迫使黑方的车沿着这些区域形成的通道向另一个构件前进。为了防止若干个黑方的车未按照设计好的通道走棋，而是去吃掉区域中的棋子并冲破这些区域，这些区域要足够厚。它的厚度是子句中所包含的最大文字数的13倍，即13k。由3.2节可知，黑方达到这个步数时，红方可先于黑方获胜。

3.2 赢棋策略

图7显示了归约模型的整体结构，它构成了n×n的中国象棋的一个局面。在此局面上模拟G3游戏，若有p(p为某个子句包含的文字的个数，文字形如x或～x)个黑车安全地停留在该子句通道上，说明G3游戏已被求解;对于n×n的中国象棋，红黑双方通过吃掉对方的帅(将)所需步数的多少来判定是否先于对方获胜。如前所述，第一步由布尔控制器中的红相走棋，它只有2种走法，红相的走棋决定了黑方的车从x或～x通道离开布尔控制器。然后由布尔控制器中的黑车走棋，接下来轮到布尔控制器中的红车走棋，它从东北角的x(～x)通道或者经由Red Clock channel离开布尔控制器，接下来黑方的车经由开关区域到达子句通道。如果某个子句通道上有p个黑方的车安全地停留在该通道上，说明该子句的布尔值为真，即布尔公式R-LOSE为真，此时G3游戏已被求解。接下来须计算n×n的中国象棋是否被最终求解。

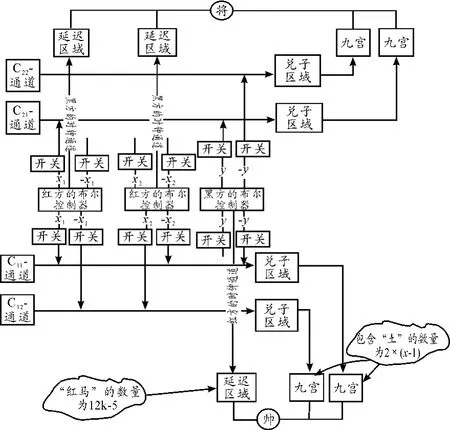
图7 一个归约模型的整体结构，其中R-LOSE= C11∨C12，C11=x1∧～x2∧～y，C12=～x1∧x2;B-LOSE=C21∨C22，C21=x1∧y，C22=～y

3.2.1 黑方的赢棋策略

假设黑方的车从x或～x通道正常离开布尔控制器，同一个布尔控制器中的红车从Red Clock channel离开。黑车离开布尔控制器需要3步(如图1所示)，经由开关到达子句通道需要6步(到达开关的那一步与离开布尔控制器的最后一步是同一步)，所以一个黑车到达子句通道共用掉m= 9步。当某个子句通道C1i上已有p(p为该子句包含的文字的个数，1≤p≤k≤12，文字形如x或～x)个黑车，则这p个黑方的车将陆续到达兑子区域，并开始与红方兑子。兑子过程所需步数计算如下:p个黑车要吃掉1个拦在通道上的红马和p -x个红炮，所以在兑子区域共用掉黑方p-x+1步。而剩下的x个黑车需要多走1步(经过一个拐点)顺利到达九宫，九宫中共有2×(x-1)个士，每2个士能兑掉1个黑方的车，所以这里需要与士进行兑子，吃掉2×(x-1)个士。而每吃掉2个士，还需再走一步吃掉另外的1个士，因此在九宫共用掉黑方2×(x-1)+2×(x-1)÷2-1= 3x-4步，最后剩下的1个黑车需要两步吃掉对方的帅。综上所述，黑方下完这盘棋共需要:m× p+p-x+1+x+3x-4+2=(m+1)×p+3x-1步，又m=9，所以总的步数为10p+3x-1。

下面计算红方。在布尔控制器中，红方的车经由Red Clock channel离开布尔控制器需要3步，同时红相用掉1步。在兑子区域，红方用p-x步吃掉对方p-x个车。在九宫中红方的士吃掉对方x-1个车，所以在九宫兑子的过程中，红方用了x-1步。红方的车到达延迟区域，这里有12k-5个对方的马，红车吃掉这些马之后，又用了2步吃掉对方的将。因此，红方所需总的步数为:3 +1+p-x+x-1+12k-5+2=12k+p。因为1 ≤p≤k≤12且1≤x≤p-1，所以红方获胜所需步数比黑方多1步。综上所述，黑方必胜。

3．2．2 红方的赢棋策略

黑方需要将p个车落在某个子句通道上，每个车到达子句通道需要m步，但有可能该子句通道对应的子句C1i=0。例如:子句C11=x1∧x2∧y1，BBC中的黑象的走棋决定了变量y1的赋值，如果黑象的走棋使得在同一布尔控制器中的黑车从～y1离开此布尔控制器，则说明变量y1被赋值为false，则子句C11=0。因此，若子句C1i=0，则之前若干个停在该子句通道上的黑车(设为y个)至少需要1步才能移动到一个能使子句的值为真的通道上。若该子句通道所包含的文字数为k(包含的最大文字数)，且该子句连接的兑子区域中的红炮的数量为1(即x的值为k-1)，则黑方吃掉帅所需总的步数为10k+3(k-1)-1+y=13k-4+ y;红方获胜所需步数为12k+k=13k。因此，当y＞4时，红方先于黑方获胜。

4 不恰当走法分析

4.1 红方布尔控制器(RBC)中可能存在的不恰当走法(BBC与RBC中可能出现的不恰当走法类似)

1)RBC中的黑车第1步到达北面的x通道，若它下一步往东走，进入Red Clock channel，在它吃掉1个红方的马后，将被上方的红炮吃掉。南面的～x通道同理。

2)RBC中的黑车通过任何途径都无法吃掉红方的相;

3)RBC中只有双方的2个车和红方的相可以主动走棋，其他棋子只能被动吃子。例如:RBC中通道拐角处的红马若走到黑车的通道上，将被黑车吃掉，而黑车不会受到威胁。

4.2 子句通道与文字通道的交叉点处可能存在的不恰当走法

黑方的车离开开关到达子句通道，只有其所在的通道对应的文字在子句中为真时，黑车才能安全地停在文字通道与子句通道的交叉点处，否则将被交叉点西南方的红马吃掉。假设该红马吃掉黑车后，被同一子句通道上的其他黑车吃掉，则红马原来位置左侧的红炮将向东移动到文字通道上。该红炮由若干个西侧的红炮保护，防止交叉点上的黑车向另一个子句通道上移动。若此黑车打算吃掉该红炮，将被红炮西侧的另一个红方的炮吃掉;若此黑车打算由此交叉点所在的文字通道反向冲入布尔控制器，则将被开关中红方的炮吃掉。

5 结论

根据各章节的论述及EXPTIME-complete问题的定义，证明n×n的中国象棋属于EXPTIME-complete问题:

1)根据2.2节的论述，可知n×n的中国象棋属于EXPTIME问题。

2)根据第3节的论述，可知在模拟的过程中，采用的是任意的一个G3游戏实例，从而说明一个给定的n×n的中国象棋局面(构建的归约模型所形成的局面)可以求解任意的一个G3游戏的实例。也就是说，存在这样的一个归约，可以将任意的一个G3游戏问题转换成n×n的中国象棋问题。根据可归约性的定义［8］:

问题A是可归约到问题B的，如果存在可计算函数f:使得对每个w，w∈A，f(w)∈B，称函数f 为A到B的归约。

由此可说明，G3游戏可归约到n×n的中国象棋。再者，G3游戏已被证明属于EXPTIME-complete问题［3］，根据EXPTIME-complete问题的定义可知，所有属于EXPTIME的问题都可归约到G3游戏。根据归约可传递的特性［8］可知:所有属于EXPTIME的问题都可归约到n×n的中国象棋。

接下来需要估算第3节中构建归约模型所需要的时间。设m为4元组包含的变量总数，对于每个变量，在归约模型中，需要用到1个布尔控制器、4个文字通道、4个开关区域、1个Clock channel以及最多4个与文字通道交叉的子句通道(可能某个文字不存在于任何子句中，所以该文字通道不与任何子句通道交叉，如图6所示)。各个组成部分都存在固定数量的处于僵局的各个棋子构成的区域。前面已提到这种区域的厚度为13k，固定数量的区域形成的总厚度为O(k)，又因为共有m个变量，所以此归约模型的总规模可以记为O(m×k)。因此，此归约模型可在多项式时间内构建完成。结合前面的论述得证:所有属于EXPTIME的问题都可在多项式时间内归约到n×n的中国象棋。

由以上两点得证:n×n的中国象棋属于EXPTIME-complete问题。

［1］AVIEZW S.FRAENKEL.Computing a perfect strategy for n×n chess requires time exponential in n［J］.JOURNAL OF COMBINATORIAL THEORY，Series A 31，1981:199-214.

［2］Robson J M.N by N Checkers is EXPTIME complete ［J］.SIAM Journal on Computing，1984，13(2):252 -267.

［3］STOCKMEYER L J，CHANDRA A K.Provably difficult combinatorial games［J］.SIAM J.Compuf，1979(8):151 -174.

［4］Lichtenstein D，Sipser M.Go is polynomial-space hard ［J］.Journal of the ACM，1980(27):393-401.

［5］Reisch S.Gobang ist PSPACE-vollständig(Gobang is PSPACE-complete)［J］.Acta Informatica，1980(13):59 -66.

［6］Ming Yu Hsieh，Shi-Chun Tsai.On the fairness and complexity of generalized k-in-a-row games［J］.Theoretical Computer Science，2007(385):88-100.

［7］Iwata S，Kasai T.The Othello game on an n×n board is PSPACE-complete［J］.Theoretical Computer Science，1994(123):329-340.

［8］Michael Sipser.Introduction to the Theory of Computation (Second Edition)［M］.China Machine Press，2006.

［9］Robert A.Hearn，Amazons is PSPACE-comp-lete［EB/ OL］.arXiv:cs.CC/0502013v1，2005.

［10］Yen Shi-Jim，Chen Jr-Chang，Yang Tai-Ning.COMPUTER CHINESE CHESS［Z］.ICCA，2004.

［11］Christos Papadimitriou.Computational Complexit-y［M］. ［S.l.］:Addison-Wesley，2001.

(责任编辑 杨黎丽)

Chinese Chess Being EXPTIME-complete

GAO Qiang，XU Xin-he
(College of Information Science and Engineering，Northeastern University，Shenyang 110004，China)

The main objective of research on computer game is looking for an ideal invincible solution of the board games.However，computational complexity is an insurmountable obstacle in the process of solving.Firstly，this article introduces EXPTIME-complete problem of computational complexity and an example of it，G3game.An n×n Chinese Chess position is constructed，and this position consists of six components which include Boolean controller，switch，the crossing of clause-channel and literal-channel，exchanging chess zone，delay zone and Nine-palace.G3game is simulated on the position，and hence it is proved that G3is reducible to n×n Chinese Chess in polynomial time，and then Chinese Chess is EXPTIME-complete.

computer games;Chinese chess;computational complexity;EXPTIME-complete;reducibility

TP301.5

A

1674-8425(2014)08-0085-07

10.3969/j.issn.1674-8425(z).2014.08.018

2014-03-26

国家自然科学基金资助项目(61370153)

高强(1980—)，男，辽宁沈阳人，博士研究生，主要从事机器博弈、计算复杂性理论研究;徐心和(1940—)，男，黑龙江哈尔滨人，教授，博士生导师，主要从事控制理论与应用、系统仿真、智能机器人、机器博弈等方面研究。

高强，徐心和.中国象棋属于EXPTIME-complete问题［J］.重庆理工大学学报:自然科学版，2014(8):85 -91.

format:GAO Qiang，XU Xin-he.Chinese Chess Being EXPTIME-complete［J］.Journal of Chongqing University of Technology:Natural Science，2014(8):85-91.