红枫分形维数中的物理机制
2014-06-27颜扬杰韦建卫程荣禄夏雪峰
颜扬杰,韦建卫,程荣禄,夏雪峰
(重庆理工大学,重庆 400054)
红枫分形维数中的物理机制
颜扬杰,韦建卫,程荣禄,夏雪峰
(重庆理工大学,重庆 400054)
采用Matlab程序计算与实验测量相结合的方法,以重庆理工大学校园内随机选取的3棵红枫为研究对象,分别测量并计算了植物整体和部分的三维空间分形维度,得出该种植物分形维度与阳光等物理因素之间的关系,以及植物生长过程中的维度变化规律。研究结果表明:植物的维度大小与其生长的物理环境具有逻辑关系。这些关系有助于深入研究高等植物的生长规律,进而为人工裁剪和控制的自然原理提供理论支持。
红枫;分形维度;计盒维数
传统的几何学不能够描述大自然的复杂性和多样性,从而使我们无法了解这些复杂性和多样性背后的机制。美国科学怪杰Mandelbrot于1975年首先提出分形几何的概念。主要用于描写云彩﹑山岭﹑海岸线或树木等自然而不规则的形状。而分形几何学在描述和理解大自然的复杂性和多样性方面具有重要作用[1-3]。十几年来,分形迅速发展,应用范围涉及自然科学的各个领域。在分形几何理论中,分形维数是最重要基本概念之一。关于分形维数的定义,主要包括Hausdorff维数、信息维数、关联维数、计盒维数、相似维数等。高等植物为构件生物,是由构件不断地生长增加而形成的,如由叶、芽、枝、花、根的反复不断地生长增加而形成整个植物体。高等植物的形态结构具有自相似特征,摘下其中任意一支枝干,将其插在地上,可看成缩小的植株。但并非植株的每一部分都生长得同样茂盛,这与它所在的生长环境(如阳光、空间分布等物理因素)有密切关系。近年来,运用分形理论对植物的各种具体特征的研究越来越多[4-7]。
分形早期用来描述一些复杂但具有严格数学规则的特殊结构,如柯赫曲线(Koch curve)、柯赫雪花(Koch snowflake)、康托尘埃(Cantor dust)、明可夫基香肠(Minkowski sausage)、谢尔宾斯基方毯(Sierpinski carpet)等等。这些图形具有严格的自相似性,将图形中任意部分放大都能得到与整体相似的形状,但是这些结构因其无穷小、无限多的迭代而无法严格存在于自然界中。同样的,自然界中的物体也难以进行严格明确的数学定义。英国数学家Falconer[8]参考生物学家的做法,通过列出分形的具体特性来给分形下定义。
本文运用分形几何的理论对重庆理工大学校园常见的一种植物的生长特性进行了研究,通过计算植物不同部分的计盒分形维度,分析得到的分形维度与植物所在的空间环境关系,为研究高等植物的生长规律提供一定的理论支持。
1 分形、分形维数与计盒维数原理
在经典的欧几里得几何中,我们已经习惯于用拓扑维度来表示空间:如零维的点、一维的线、二维的平面、三维的立方形,其所表示的维度都是整数。然而,大自然中的山峰、树木、云朵等物体因其复杂和不规则性并不能用简单的线段、矩形、三角形和圆等规则的图形来描述,分形因此诞生。它能很好地描述这些复杂的物体,所得到的维度并非整数,而是分数,称为分形维数。例如计算出柯赫曲线的计盒维数为1.261 8,它大于线的拓扑维度1。原因是柯赫曲线可无限进行下去,将几乎覆盖整个平面。
试想有一条单位长度的线段,用长为r的小线段去覆盖它,需要1/r个小正方体;如果是单位边长的正方形,则需要1/r2个小正方形;如果是单位边长的立方体,覆盖它需要1/r3个小正方体。值得注意的是r的指数和被覆盖的对象的维度是相同的,这并非偶然。一般我们可以用“盒子”来覆盖任意形状的图形。
设A是Rn空间的任意非空有界子集,对任意的一个r>0,Nr(A)表示用来覆盖A所需的边长为r的n维立方体(盒子)的最小数目。如果存在一个数d,使得当r→0时,有

那么称d为A的计盒维数(简称盒维数)。盒维数为d,当且仅当存在一个正数k使得

由于方程两边都为正,因此可以对方程两边取对数,得

这里舍去了logk这一项,因为它是常数项。当r→0时,分母趋于无穷大。
在实际计算中,可以使用不同边长的立方体来覆盖图形,得出不同r值下的Nr(A),再以logr为横坐标、logNr(A)为纵坐标的双对数坐标系中描出点(logri,logNri(A)),最后由这些点拟合出来的直线的斜率的负值便是图形A的维数。
2 样本植株
图1为测量维度的红枫样本植株。图1(a)~(c)分别为样本1、样本2、样本3。

图1 测量维度的红枫样本植株
3 测量方法及所得数据
首先在空间中建立三维直角坐标,选取适当的原点,本次测量都将原点取在离植株较远的位置,确保植株所有枝干都能在坐标系的第一象限中。定好原点,确定好主枝干的坐标位置,便可开始测量每一级分叉点的空间坐标,即分叉点在xz平面和y-z平面投影坐标,并记下是第几级分叉点。一人测量,一人记录。测量工具为米尺,其精度为 mm,本次研究的精度为 cm,且数据取整数。
4 结果及分析
根据测量所得数据,已知2个分叉点的坐标便可在空间确定一条直线,该直线即为样本枝干的模拟。利用Matlab[9]软件建立一个6行n列的矩阵,n为所测量的样本的枝干数目,前3行为一个分叉点的坐标,记为x1,y1,z1;后3行为另一个分叉点的坐标,记为x2,y2,z2。接着在z1到z2之间每隔0.01取一个数,在x-z平面利用直线的点斜式公式便可算得该线段上的其他点的x坐标,同理,在y-z平面得到该线段上其他点的y坐标。这样一系列的点在空间构成一条线段,重复以上步骤得到三维立体数字样本模型(见图2),利用前面所得的模型可计算其盒维数。首先将空间分割成一个个“盒子”,并为每个“盒子”按其空间位置编号,如(2 3 4)表示“盒子”的x坐标在r到2r之间;y坐标在2r到3r之间;z坐标在3r到4r之间,其中r为“盒子”边长。每条线段上的点依次判断在哪个“盒子”里,最后去掉编号相同的“盒子”,所得的便是该样本模型在空间中占据的“盒子”数,记为Nr。改变“盒子”边长重复计算得到在不同边长时占据的“盒子”数。最后在双对数坐标下描出对应的点,并运用最小二值法拟合直线(见图3),所得直线斜率的负值即为盒维度。
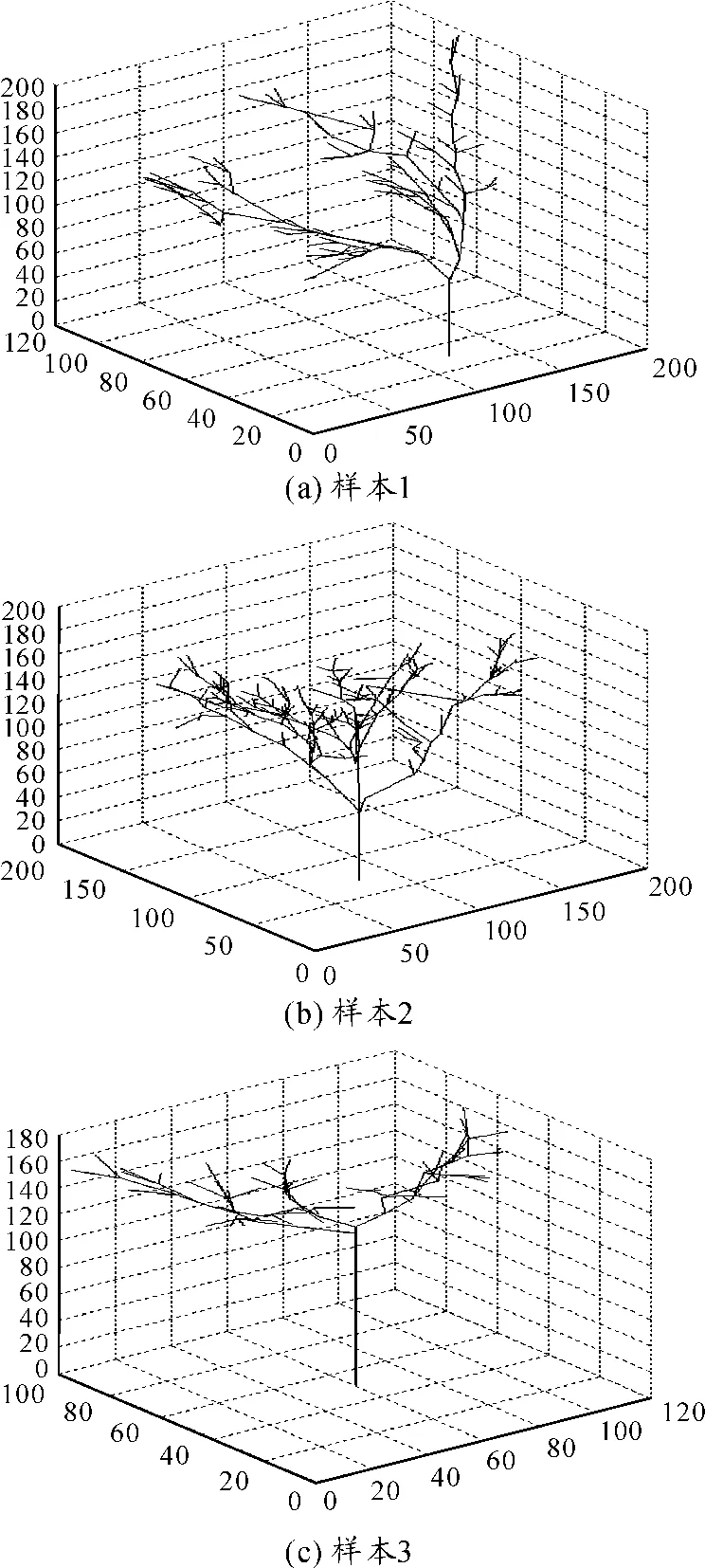
图2 三维立体数字样本模型
图3为3个样本数据在双对数坐标中拟合的直线。拟合图纵坐标为盒子数的对数,横坐标为盒子边长对数。data1,data2对应样本1;data3,da-ta4对应样本2;data5,data6对应样本3。

图3 3个样本数据在双对数坐标中拟合的直线

表1 3个样本的维度结果
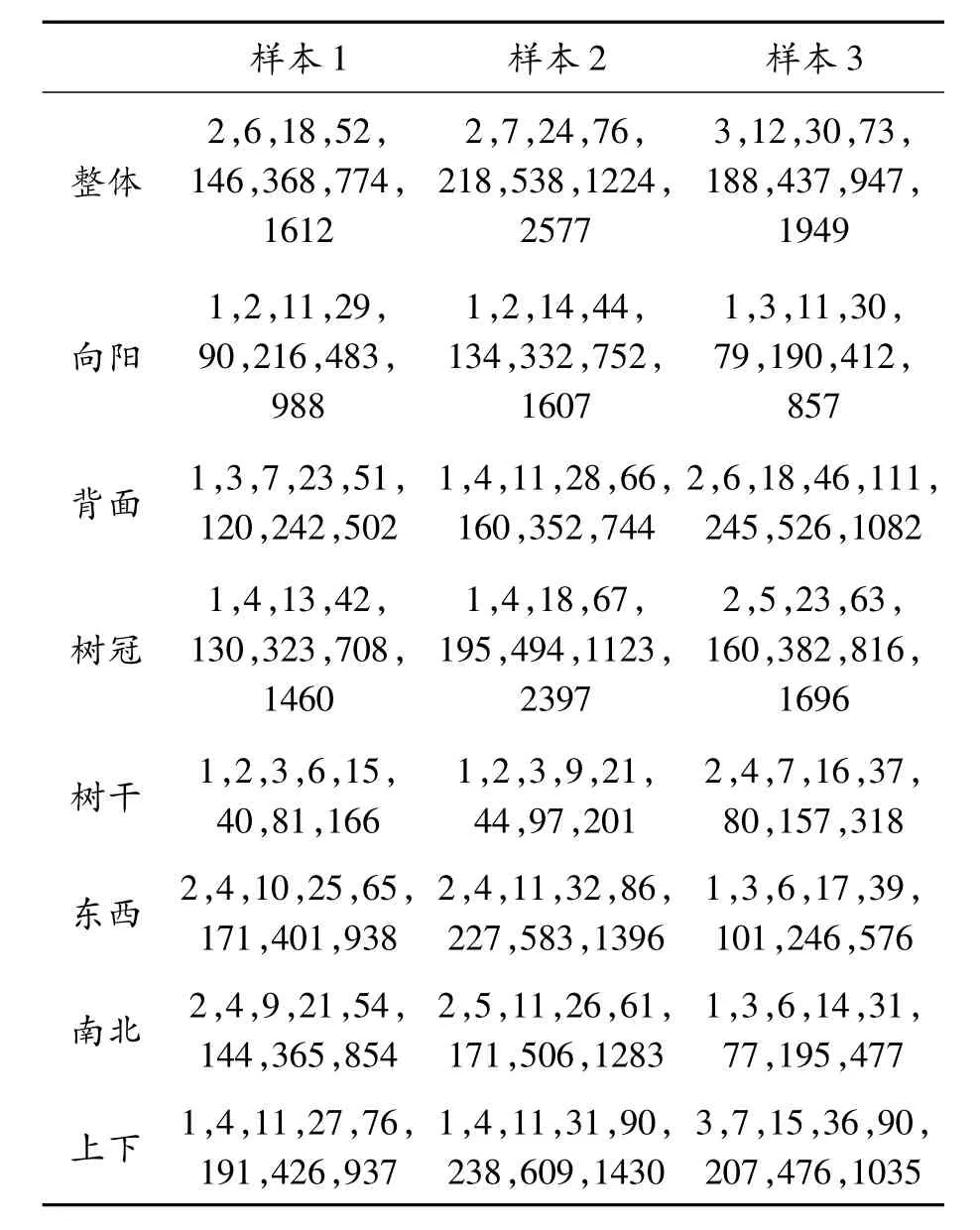
表2 3个样本在不同尺寸下的盒子覆盖数
由于同种植物应有相同的生长规律,所得的整体维数应该接近。计算结果表明:3棵红枫的整体维数接近,符合实际情况。
在向阳的方向得到的维数都略大于背阳的方向。从得到的图像中也可以看出:向阳方向的图像更为复杂,在实际中表明植物向阳方向将生长得更为茂密,植物有向光方向生长的趋势。向阳部分的维度结果表明:阳光能够提供更多的生长动力,使其更多地进行分叉、抽枝,以占领更多空间区域而获得更多能量,进而促进整个植株的整体优势地位。
植物的树冠部分与靠近地面的树干部分的维数有较大的差异,在实际中表明植物越往上生长,其结构会更为复杂。在底部主枝干分级少,往上生长分级越多,各级枝干越多,生长茂密,横向宽度也增大。该植物样本早期时维度较小,随着生长发育的进行维度逐渐增加,当成年后基本确定下来。因此,想要使得植物生长较为高大,则需要不断地修剪多余的分叉,使得植株在维度较低情况下继续分叉生长。
计算结果如表1和2所示,3棵红枫植株的整体分形维数分别为1.395 1,1.482 7,1.308 0。本次研究所得的图像是在三维空间中用描点的形式模拟实际中红枫植株的形状,忽略了植株枝干的粗细,所得图像在三维空间中占少量的体积,得到的维度比实际数据略有偏低,但同时也考虑了样本1入直径数据的计算情况。结果发现:各个部分的维度都有增加,但是它们之间的相对关系并无根本性的变化,因此并不影响结论,故认为此次维数计算是合理的。
5 结束语
本次研究对植株分叉点的坐标采取人工测量,测量过程对树叶的空间占据有所忽略,但据实物情况来看,叶子数基本正比于枝干的长度,枝干的维度也就基本反映了叶子的各部分情况,所以定性结果是较为准确的。若能采用大型三维投影设备可得到植株的全部信息,增加样本数量,再对程序进行改进,加上植株的实际直径,得到的结果将更科学、更有说服力。
[1] 陈红,夏青,左婷,等.基于纹理分析的香菇品质分选方法[J].农业工程学报,2014,30(3):281-287.
[2] 单立山,李毅,任伟,等.河西走廊中部两种荒漠植物根系构型特征[J].应用生态学报,2013,24(1):25-31.
[3] 李志臣,姬长英.基于图像分析的杂草分形维数计算[J].农业工程报,2006,11(11):175-178.
[4] 朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社,2011.
[5] 温芝元,曹乐平.椪柑果实病虫害的傅里叶频谱重分形图像识别[J].农业工程学报,2013,29(23):159-164.
[6] 丁雪娇,韩红,庞彩菊,等.砂砧薹草和假牛鞭草种群空间分布格局的分形特征[J].浙江农林大学学报,2013,30(2):220-225.
[7] 袁津生,姚宇飞.基于分形维度的叶片图像识别方法[J].计算机工程与设计,2012,33(2):670-673.
[8] 张济忠.分形[M].北京:清华出版社,2011.
[9] 张波,沈火明.基于Matlab的壳体有限元分析[J].重庆理工大学学报:自然科学版,2010,24(12):77-81.
(责任编辑 刘 舸)
Physical Mechanism of Fractal Dimensionality of Red Maple
YAN Yang-jie,WEI Jian-wei,CHENG Rong-lu,XIA Xue-feng
(Chongqing University of Technology,Chongqing 400054,China)
Combining experimental measurement and the calculation of Matlab code,the physical factors of plant growth have been analyzed through fractal dimensionality data.Three red maples were selected randomly and measured.The space coordinates of the branches were recorded and loaded into computer.The fractal dimensionalities were calculated and analyzed with Matlab code through boxcounting method.We find the relevance between the sunlight and the fractal dimensionalities.The law of the dimensionality changing of the plant has also been studied.The results indicate that there is an inevitable logical relationship between physical environment and dimensionality of the plant.The relationship will assist the investigation of plant growth rhythm.Furthermore,it will benefit to the natural principle of artificial clip.
red maple;fractal dimensionality;box-counting dimension
O29
A
1674-8425(2014)07-0127-05
10.3969/j.issn.1674-8425(z).2014.07.025
2014-02-20
国家自然科学青年基金资助项目(11204391);重庆市教委项目(KJ130831);2013年校级科研立项项目(GD15)
颜扬杰(1992—),福建泉州人,主要从事计算机仿真模拟数值计算研究;通讯作者韦建卫(1980—),男,河南焦作人,博士,副教授,主要从事纳米材料与器件方面的研究。
颜扬杰,韦建卫,程荣禄,等.红枫分形维数中的物理机制[J].重庆理工大学学报:自然科学版,2014(7): 127-131.
format:YAN Yang-jie,WEI Jian-wei,CHENG Rong-lu,et al.Physical Mechanism of Fractal Dimensionality of Red Maple[J].Journal of Chongqing University of Technology:Natural Science,2014(7):127-131.
