接受孔元件的周向速度系数模型与验证

张建超，王锁芳，王春凤，3，徐 昊，马 力

(1.江苏省航空动力系统重点实验室，南京 210016; 2.南京航空航天大学能源与动力学院，南京 210016; 3.江铃汽车股份有限公司，南昌 330001)

接受孔元件的周向速度系数模型与验证

张建超1，2，王锁芳1，2，王春凤1，2，3，徐 昊1，2，马 力1，2

(1.江苏省航空动力系统重点实验室，南京 210016; 2.南京航空航天大学能源与动力学院，南京 210016; 3.江铃汽车股份有限公司，南昌 330001)

分析简化预旋系统的流路和典型工况下接受孔附近流场，建立预测接受孔周向速度系数的数学模型，在一系列工况下对盖板预旋系统进行了CFD分析，并将计算结果和模型预测结果进行对比，证明采用该模型预测周向速度系数的有效性。研究结果表明:接受孔内流动按流动形态可以分为3个区域，影响因素主要有旋流比、长细比和进气攻角，结合几何关系建立了数学模型，在预测周向速度系数时可达到一定精度;与原始模型相比，利用周向速度系数模型修正接受孔元件后，一维流路的预测结果和CFD计算结果吻合较好。

预旋;接受孔;周向速度系数;一维流路

在现代航空发动机中，通常采用预旋的方式向涡轮叶片供应冷气。冷气从压气机引到预旋系统，在预旋喷嘴内膨胀加速并扭转流动方向，产生较大的周向速度，方向与下游旋转系转向一致，穿过接受孔进入旋转系。此时，由于气流在旋转系中的相对速度降低使得旋转系感受到较低的温度，从而产生“降温”的效果，提高冷却品质。最终冷气进入涡轮叶片进行冷却。

国内外研究人员对预旋系统及各个元件开展了大量研究。Popp［1］对预旋盖板和喷嘴的结构进行了CFD分析［2］，提出设计的合理化建议;Javiya等［3］研究了预旋系统内部的流动与换热问题; Lewis［4］探讨了预旋结构流动换热的机理;Debuchy等［5］研究了多种预旋条件下的转静腔内的旋流; Bricaud［6－7］通过试验分析了预旋转静系中的流动特点;Dittmann研究了直导预旋系统流动的一维特性［8］和预旋元件(如预旋喷嘴、旋转孔等［9］)的流量特性;Idris［10］研究了进气攻角对旋转孔流量特性的影响规律。国内近年来在预旋降温方面开展的研究也越来越多，王锁芳［11］、何振威［12］等分别对不同形式预旋结构的流动与换热开展了试验研究;刘波［13］通过试验验证了预旋喷嘴的流量特性。国内在涡轮叶片冷却研究时涉及到了对旋转孔流动特性的分析［14－15］，但在进行空气系统建模时仅考虑旋转孔的流量特性［16］，没有专门针对接受孔的速度特性开展研究。

本文为弥补接受孔元件对周向速度预测的不足，分析了预旋流路的结构和典型工况下接受孔附近的流动特点，提出接受孔周向速度系数，基于流动特征建立数学模型，验证了模型的有效性，最后将该模型写入一维流路计算程序以修正接受孔元件的数学模型。对比修正前后的计算结果，说明采用这种修正方法对提高流路预测精度是可行的。

1 预旋结构与典型流场分析

1.1 典型盖板预旋流路的结构

图1(a)、(b)分别是典型的航空发动机预旋系统结构和简化流路，接受孔的位置如图1(a)圈内所示。

航空发动机空气系统的预旋结构在设计阶段就需要对预旋温降和流阻有较高精度的预测。在计算接受孔下游的旋转盘腔的旋流比时，需要接受孔出口处冷气的参数(如轴向速度、周向速度和温度等)，旋转盘腔旋流比又是分析盘腔的风阻温升、离心增压效应等的重要数据，故掌握接受孔的特性对预旋结构温降流阻特性预测精度的提高有重要意义。接受孔的几何结构对出口冷气的周向速度和流量特性有重要影响，因此有必要对接受孔速度特性和流动特性开展研究。

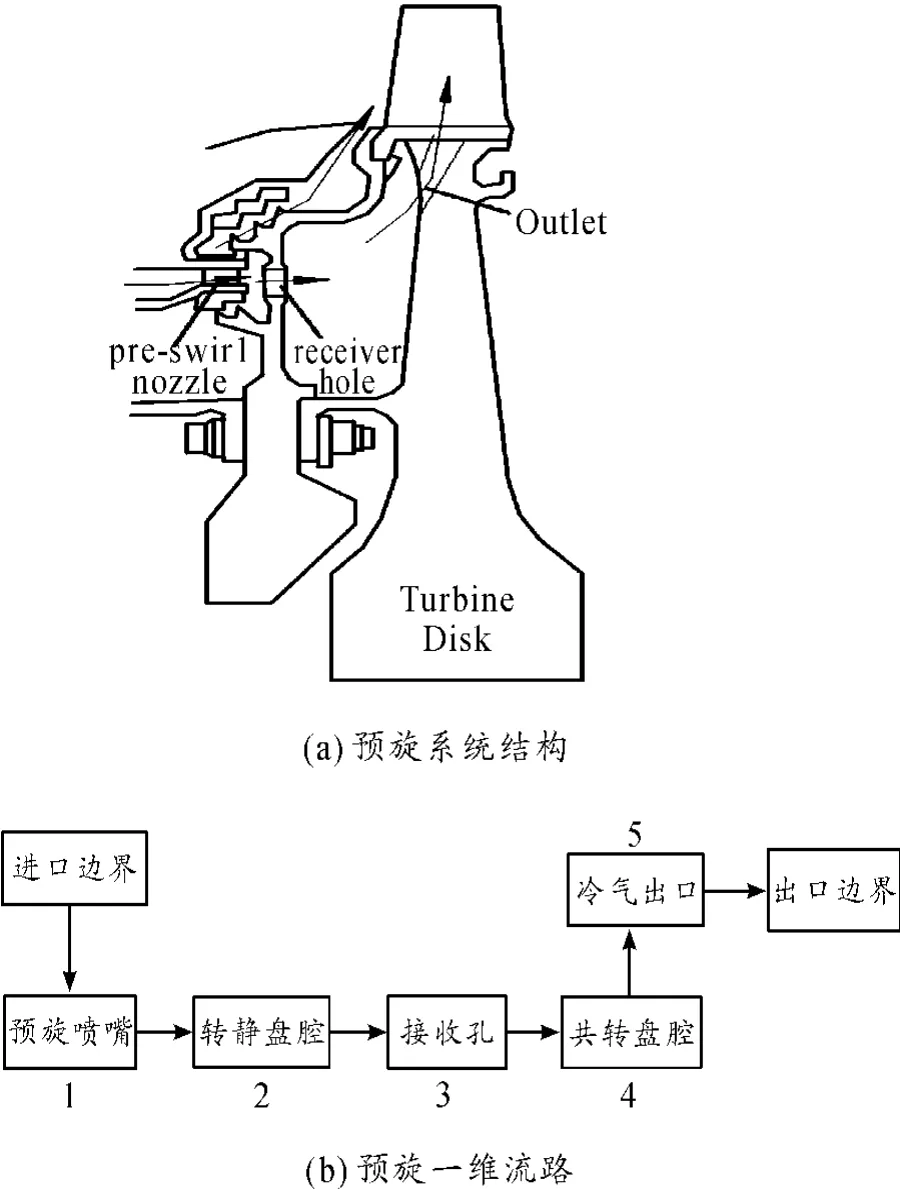
图1 预旋系统

用来冷却高压涡轮叶片的冷气供气结构如图1(a)所示，简化成图1(b)所示的流路。对预旋系统的共转盘腔(图1(b)中元件4)而言，旋流比是计算风阻温升所需的重要参数，盘腔内部的平均旋流比通过迭代得到。

在进行预旋系统及空气系统流路网络建模时，通常把旋转接受孔内的流动简单地作为刚体旋转来处理，对流体进出接受孔的流动细节考虑不多，这与实际情况有较大的差别。下面通过典型工况的流场进行说明。

1.2 典型工况下接受孔流场分析

CFD计算模型如图2所示，采用同类模型的试验值验证了数值方法的正确性，计算值和试验值的误差不大于6%。根据结构的周期性，建立模型的1/20作为计算域。采用非结构化四面体网格进行网格划分，壁面附近用三棱柱网格进行加密，经过网格独立性试验后选定网格数在23万左右的网格进行计算。将转静腔分为两部分:左侧与预旋喷嘴相连，设置为静止域;右侧与接受孔、共转腔等相连，设置为旋转域。交界面采用冰冻转子模型。所有壁面绝热无滑移。进口为压力进口，给定进口总压和总温，气流垂直于进口面进入预旋喷嘴;出口边界为压力出口，给定出口静压。求解器使用CFX商用软件，对流项和湍流采用高分辨率格式，高雷诺数区域里湍流的模拟采用标准k－ε模型，壁面低雷诺数区域附近采用scalable壁面函数。计算时监控出口相对总温和流量。当各个方程残差小于10－5，出口相对总温和流量值趋于平直且随迭代变化极小时，认为计算收敛。

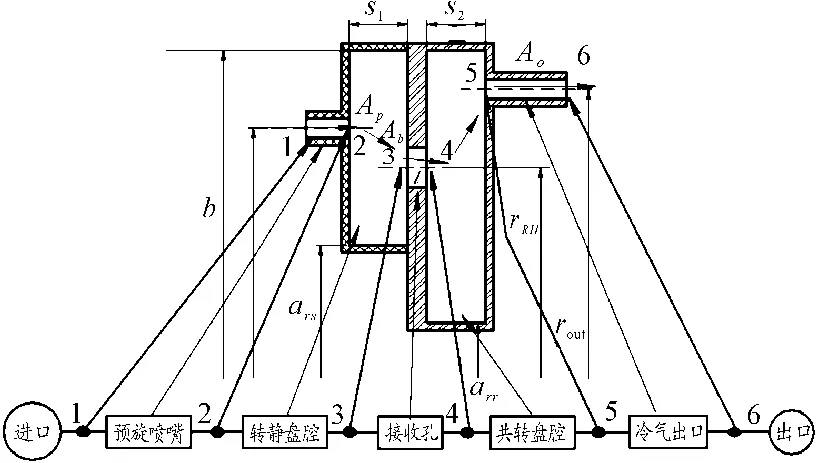
图2 计算模型及一维流路

重要的结构参数在图2中标出，各个元件的进出口截面和一维流路的节点对应关系如图2所示。预旋流路中转静盘腔和共转盘腔的结构内外半径相同，b=150 mm，内半径 arr/b=0.533，ars/b=0.667;预旋喷嘴、接受孔和冷气出口元件各20个，径向位置分别为Xp=rp/b=0.867;Xb= rb/b=0.8，Xout=rout/b=0.933;面积比Ap∶Ab∶Ao= 1∶4∶1，盘间距G1=G2=s1(2)/b=0.1。转静盘腔的内外围屏静止，将预旋喷嘴安装在静盘上，预旋角为30°。

图3是盖板预旋系统在Reω=5.554×106时接受孔附近的速度矢量图。可以看出:气流进入接受孔前周向速度很大，流出接受孔后气流的速度方向发生明显变化，与孔轴线的夹角减小。流体以一定角度进入接受孔，按各部分的流动形态可以把孔内分为3个区域:①气流直接穿过接受孔进入下游共转盘腔;②冲击接受孔壁面，而后流动方向转向与孔轴线一致;③气流方向与壁面另一侧夹角过大，孔内明显流动分离，几乎没有上游流体经过。

流体流经接受孔时通过和孔壁面发生相互作用改变速度大小和方向。影响因素主要有流体进入接受孔的角度，接受孔的长度、直径、径向位置和转速等，处理成无量纲的形式则有接受孔进口旋流比Srin、接受孔长细比l/d、进气攻角α。

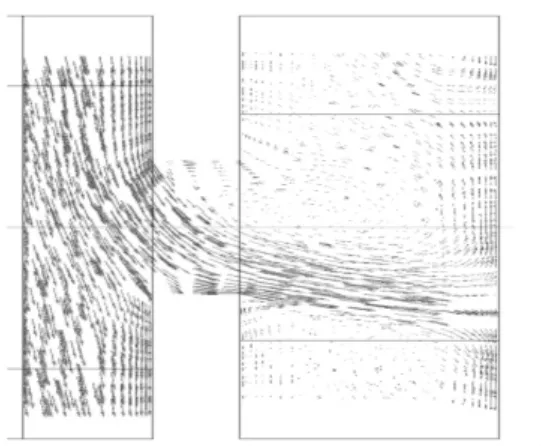
图3 接受孔附近的速度矢量图Reω=5.554×106

2 周向速度系数及物理意义

从结构上看，接受孔通常是一类大直径孔，长细比相对较小，不宜作为一般意义上的限流孔考虑。在构成连通转静盘腔和共转盘腔的通道时，接受孔输送的流量和周向动量对下游共转盘腔的旋流比有重要影响，进而影响盘腔元件的温升、流阻和离心增压等。

定义接受孔周向速度系数为

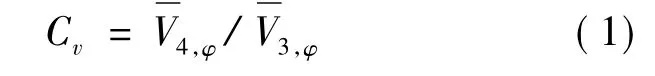
周向速度系数Cv写成下面的形式:

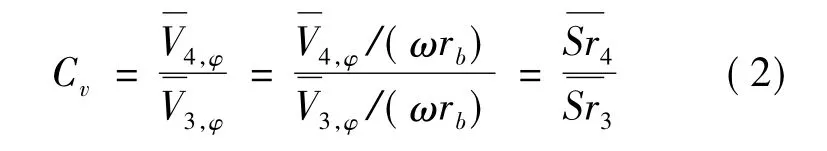
式(2)中的Sr3和Sr4分别是接受孔进口和出口处的平均旋流比。在盘腔内对周向速度取平均，使用盘腔元件的平均旋流比来衡量旋流，则Cv反映了上下游盘腔元件平均旋流比之比。这也意味着通过调整接受孔的尺寸如直径、长度、径向位置等影响出口周向速度的结构参数，可以在一定程度上调整上下游盘腔元件的旋流比，进而对受旋流比较大的“离心增压”作用施加影响。

对共转盘腔内流体的周向运动采用均匀化处理后，接受孔出口(见图2节点4)和冷气出流孔的进口(见图2节点5)的旋流比相同，即

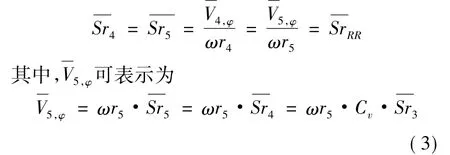
由式(3)得到考虑接受孔影响的冷气出流孔的进口的周向速度。

3 周向速度系数的模型

依据来自转静盘腔的气流穿过接受孔的不同状态建立接受孔简化模型，如图4所示。其中: Across为接受孔的直通面积;l为接受孔长度;d为接受孔直径;α为上游来流与接受孔轴线夹角(进气角度)。已知上游来流的周向速度V3，φ、轴向速度V3，z、接受孔进口前的旋流比Srin及几何参数，做以下基本假设:

1)接受孔进出口附近及孔内的流动均匀稳定，不考虑黏性影响;接受孔的流通面积可以分为2部分:一部分气流直接穿过接受孔，面积为Across;另一部分气流冲刷接受孔内壁面。

2)假设经过直通区域的气流不改变运动状态，即出口处旋流比Srout=Srin;气流与接受孔的旋转壁面充分作用后，周向速度和旋转系速度相同，即Srout=1;不计气流过孔前后的压力变化。

3)出口气流的旋流比由2)中所述2部分流体按流通面积所占比重加权得到，即

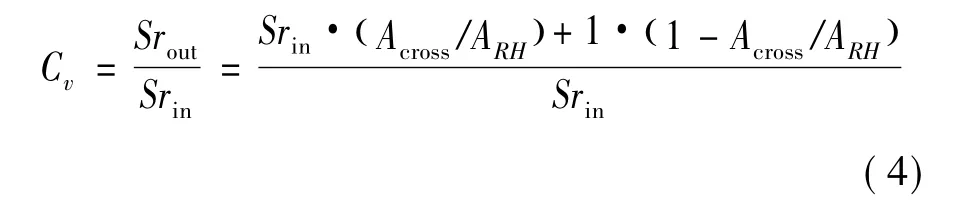
综合式(4)～(8)，可计算出接受孔的周向速度系数Cv。

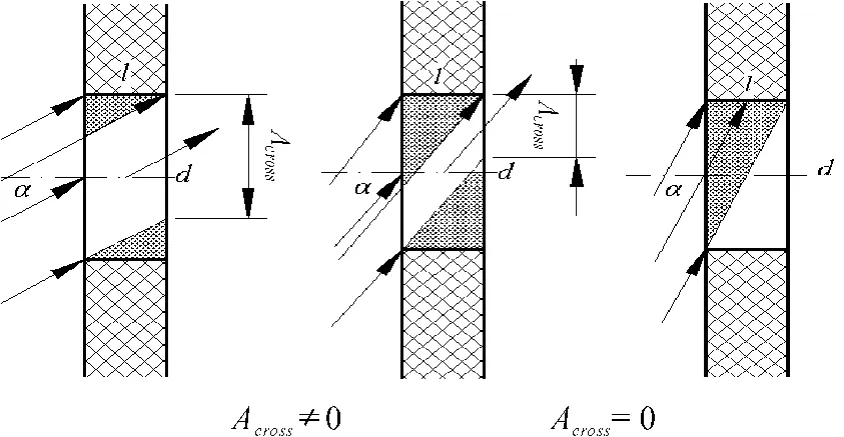
图4 接受孔模型

4 模型预测精度

盖板预旋系统的接受孔有3个重要的结构参数:面积、长度和径向位置。这里将这3个参数转换成接受孔和预旋喷嘴的面积比Ab/Ap、接受孔的长细比l/d和径向位置Xb，通过数值计算得到相关数据，分析结构参数变化对接受孔Cv的影响规律。将算例数据代入前述模型以检验模型。

本节图中的CFD结果按定义式计算，Model结果按数学模型(式(4)～(8))计算得到。

图5是盖板预旋系统的接受孔周向速度系数随接受孔和预旋喷嘴面积比的变化。可以看出:在计算范围内的不同径向位置处，接受孔面积小于4倍预旋喷嘴面积时，改变接受孔面积对接受孔出口的周向速度有显著影响;接受孔面积变得更大时，对周向速度的影响变小，减小的幅度逐渐变小，降到极小值后又略微增大。

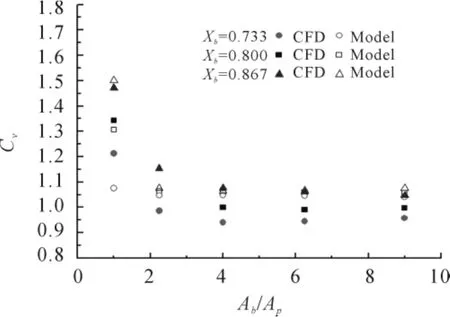
图5 接受孔的Cv随面积比的变化

图6是不同接受孔面积下，接受孔的周向速度系数随径向位置的变化。可以看出:对于各个面积的接受孔，径向位置越大时周向速度系数也越大。

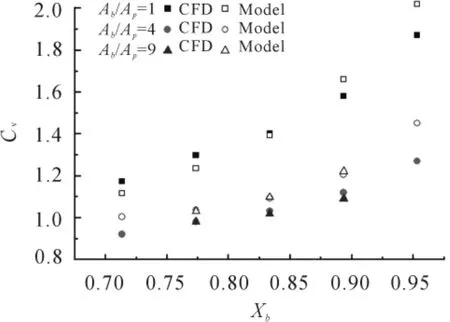
图6 接受孔的Cv随接受孔径向位置的变化

图7是接受孔的Cv随长细比的变化。可以看出:Cv随着长细比增大而增大，并逐渐趋向稳定。不同面积的接受孔的Cv随长细比的增大有相同的规律。

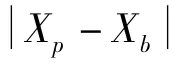
另外，本节模型预测结果没有进行黏性修正，即Xvis=1，但修正后可以获得几乎完全一致的结果。因此计算结果表明:采用式(4)～(8)估算Cv是合理的，并可提供具有一定准确性的预测。

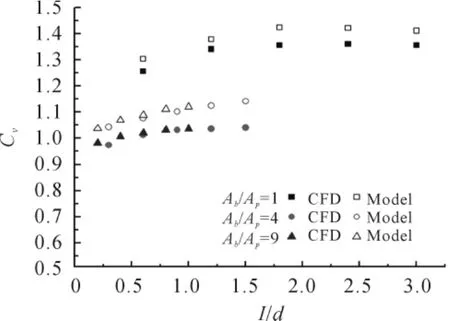
图7 接受孔的Cv随接受孔长细比的变化

5 模型应用于一维流路计算

为验证本文建立的周向系数模型是否正确有效，本节编写一维流路求解程序，计算一组典型工况。通过对比引入周向系数模型前后的计算结果，证明其合理性。

与整机空气系统的多元件类型、多分支的复杂流路相比，预旋流路在简化后仅有一条(不考虑对预旋降温没有直接贡献的封严)，且元件数目和种类也较少，应用顺序解法较为方便［16］。而求解流体管网常用的流体网络解法在计算复杂管路时更加便捷，对简单流路并没有特别的优势。综合考虑，本节采用顺序法求解预旋流路。流路中各元件的数学模型参见文献［7，8，16］。典型工况如表1所示。

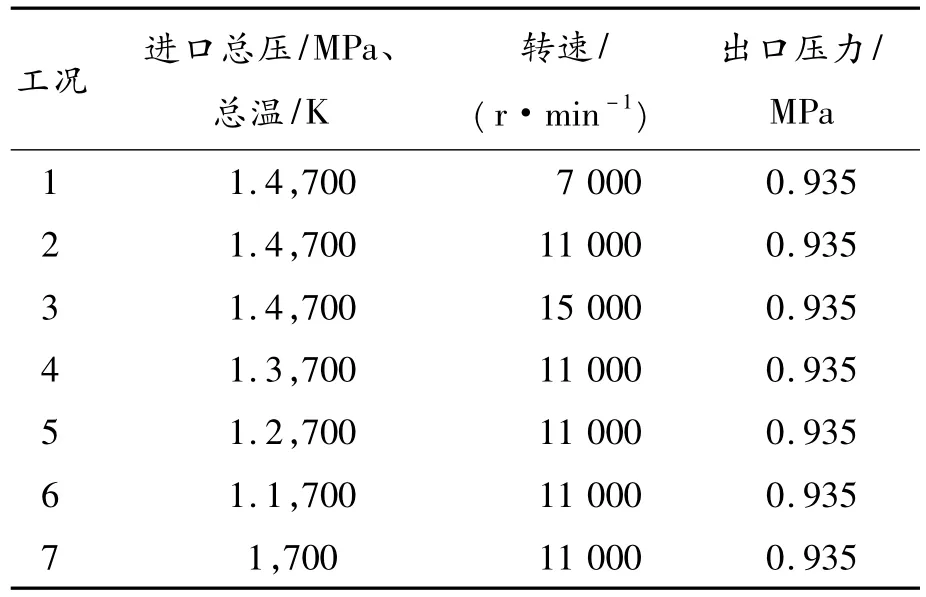
表1 典型工况表

工况1～3的进口压力相同，旋转件的转速逐渐增大，则流量大致相同，略有增加，旋转雷诺数逐渐增大;工况4～7的旋转件转速相同，进口压力逐渐降低，旋转雷诺数基本一致，流量依次减小。

将CFD仿真得到的元件特性参数作为已知量输入一维流路计算程序，在与CFD仿真相同工况下进行计算，得到流路节点参数和出口参数。

以CFD计算结果为基准值，定义误差系数

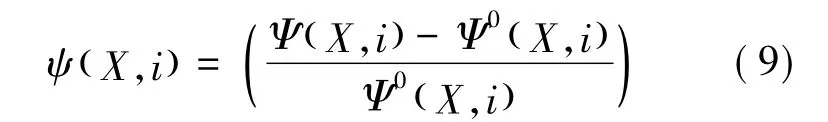
式(9)中:ψ( X，i)表示物理量名称(温度、压力等)在节点编号i位置的相对误差;ψ表示一维程序计算结果;ψ0表示CFD的结果。

图8是不同工况下各节点总压的相对误差。可以看出:修正前后总压误差的量级相当，修正后接受孔出口以后的节点(Node5、6)误差略有降低。

图9是不同工况下各节点总温的相对误差。可以看出:修正后接受孔下游节点的误差明显降低，各个工况下的误差分布也较集中，为正偏差。引入周向速度系数后，接受孔下游的计算更加准确。图10是修正前后典型工况下的流量误差，修正前后流量误差变化不大，除工况1的误差较大外，各工况下误差不大于8%。

图11、12是修正接受孔模型前后共转盘腔的旋流比和预旋流路出口相对总温的计算结果对比。可以看出:在各个工况下修正后共转腔的旋流比更接近基准值;个别工况下旋流比和基准值吻合很好;大部分工况下，修正前预旋流路出口相对总温高于基准值，也高于修正后的预测结果;对于计算的典型工况，修正后的结果相对更加接近基准值，并略高于基准值。这对工程而言是偏安全的。

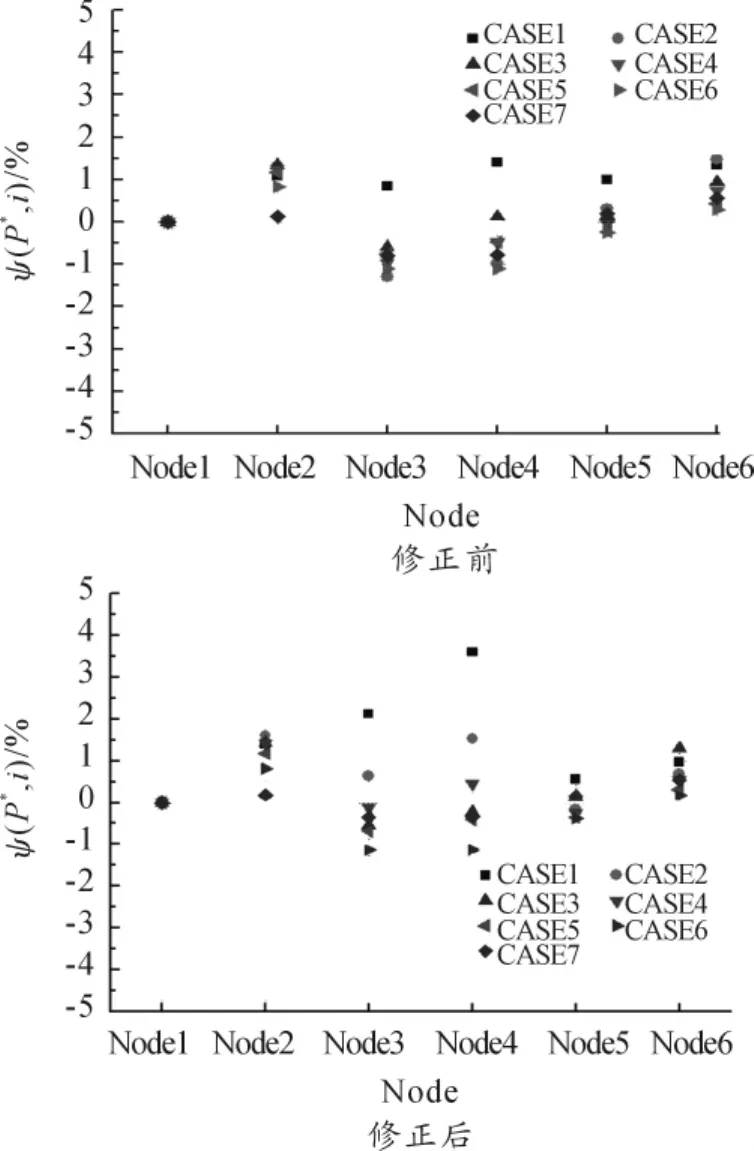
图8 各节点总压的相对误差

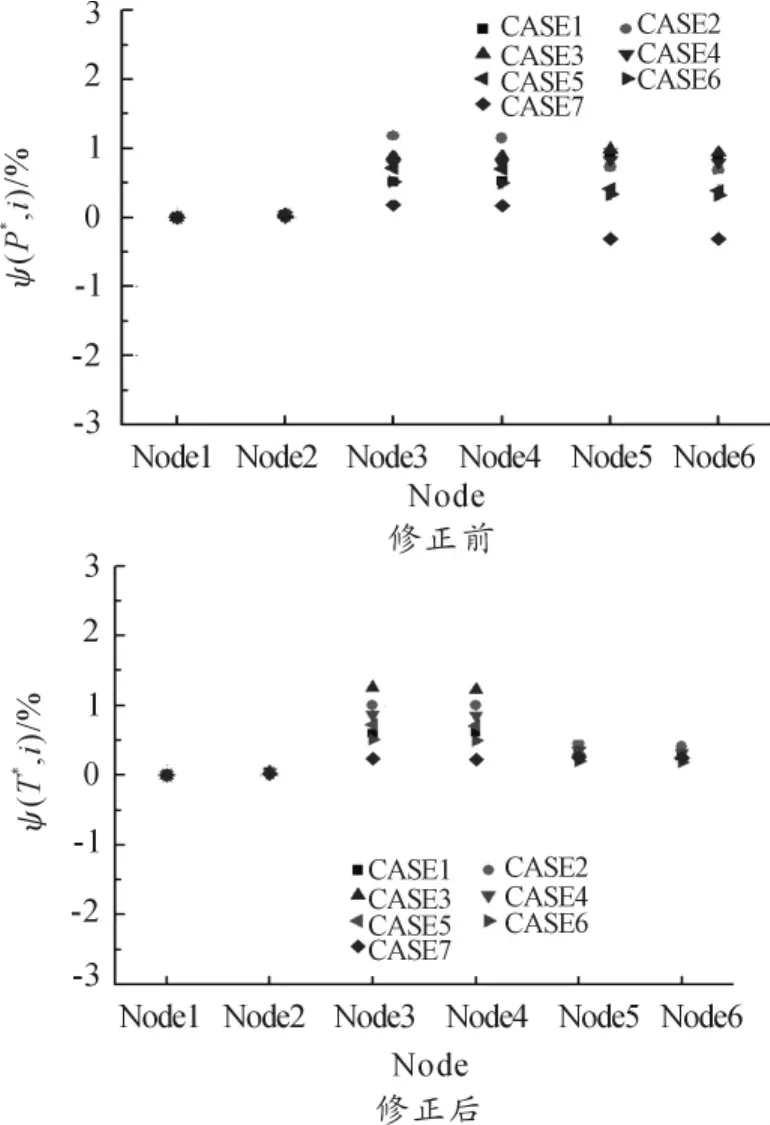
图9 各节点总温的相对误差

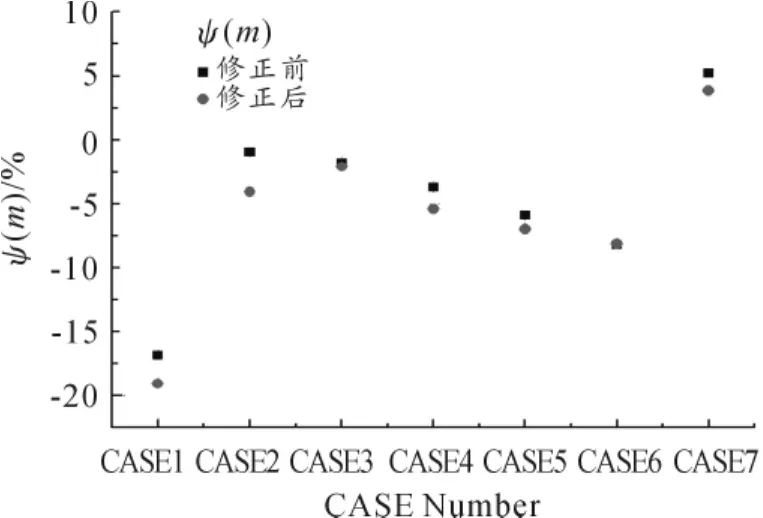
图10 修正前后典型工况下流量误差

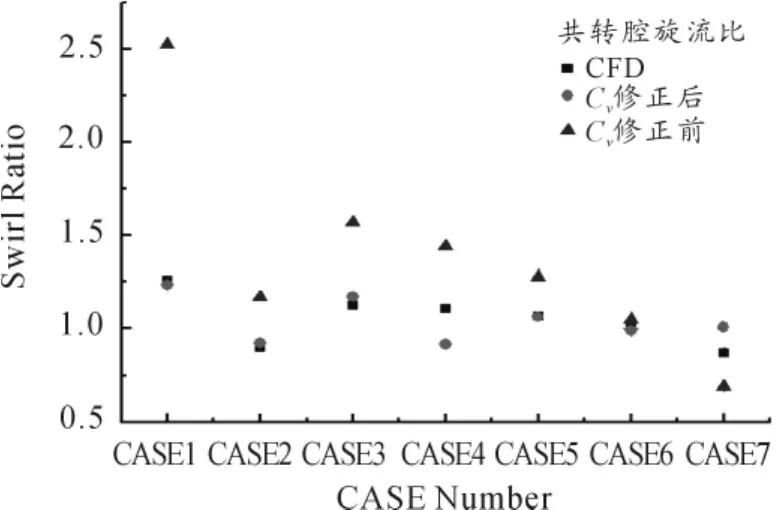
图11 修正前后典型工况下共转腔的旋流比

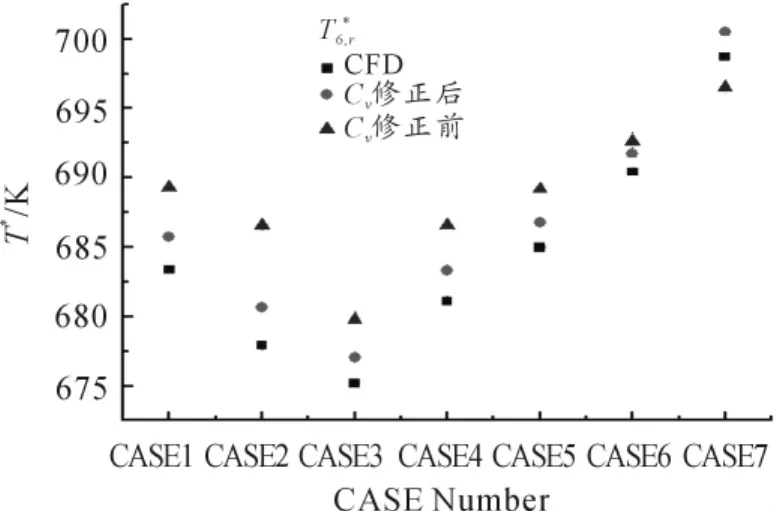
图12 修正前后典型工况下流路出口的相对总温

可见，采用接受孔周向速度系数对接受孔数学模型进行修正对提高预旋流路出口温度和压力的预测精度是有效的。

6 结论

1)本文建立的接受孔周向速度系数数学模型的计算值和CFD结果较一致，可提供有一定准确性的预测。

2)周向速度系数模型以接受孔附近流动的均匀性假设为基础，实际使用时越接近这种假设，数学模型的预测值越准确。

3)在一维程序的接受孔元件引入该模型进行修正后，典型工况的共转腔旋流比、温降一维计算结果误差减小，表明修正后的结果更加接近基准值。一维计算程序的各物理量误差小于8%，满足工程设计需要。

［1］ Popp O，Zimmermann H，Kutz J.CFD－analysis of coverplate receiver flow［C］//Burmingham.UK:ASME，1996: 43－49.

［2］ 白长安，吴伟蔚，李金国，等.变排量叶片机油泵CFD分析［J］.机床与液压，2013，41(1):76－79.

［3］ Javiya U，Chew J W，Hills N J，et al.CFD analysis of flow and heat transfer in a direct transfer preswirl system［J］.Journal ofTurbomachinery，2012，134(3):31017－31019.

［4］ Lewis P，Wilson M，Lock G，et al.Physical interpretation of flow and heat transfer in pre－swirl systems［C］//Barcelona，Spain:American Society of Mechanical Engineers，2006:1291－1300.

［5］ Debuchy R，Abdel Nour F.An Analytical Modeling of the Central Core Flow in a Rotor－Stator System With Several Preswirl Conditions［J］.Journal of Fluids Engineering，2010，132(6):61102－61111.

［6］ Bricaud C，Richter B，Dullenkopf K，et al.Stereo PIV measurements in an enclosed rotor－stator system with preswirled cooling air［J］.Experiments in Fluids，2005，39 (2):202－212.

［7］ Bricaud C，Geis T，Dullenkopf K，et al.Measurement and analysis of aerodynamic and thermodynamic losses in preswirl system arrangements［C］//Montreal，Que.Canada: American Society of Mechanical Engineers，2007:1115－1126.

［8］ Dittmann M，Dullenkopf K，Wittig S.Direct－transfer preswirl system:A one dimensional modular characterization of the flow［C］//Atlanta，GA，United states:American Society of Mechanical Engineers，2003:383－388.

［9］ Dittmann M，Geis T，Schramm V，et al.Discharge coefficients of a preswirl system in secondary air systems［J］.Journal of Turbomachinery，2002，124(1):119－124.

［10］Idris A，Pullen K R.Correlations for the discharge coefficient of rotating orifices based on the incidence angle［J］.Proceedings of the Institution of Mechanical Engineers，Part A(Journal of Power and Energy)，2005，219 (A5):333－352.

［11］王锁芳，朱强华，栾海峰，等.高位预旋进气转静盘腔换热实验［J］.航空动力学报，2007，22(8):1216－1221.

［12］何振威，冯青，刘松龄，等.带盖板预旋系统的流动实验［J］.推进技术，2011，32(5):654－657.

［13］刘波，王永红.预旋喷嘴流动特性试验研究［J］.燃气涡轮试验与研究，2009，22(03):45－46.

［14］李莉，徐国强，丁水汀，等.涡轮叶片尾缘新型结构的换热与流阻［J］.中国民航大学学报，2008，26(5):29－31，35.

［15］王开，徐国强，陶智，等.直径比对冲击气膜组合冷却流动与换热的影响［J］.航空学报，2008，29(4):823－828.

［16］陆海鹰，杨燕生，王鸣.航空发动机空气系统特性的数值模拟［J］.航空发动机，1997(1):6－13.

［17］曹玉璋.航空发动机传热学［M］.北京:北京航空航天大学出版社，2005.

(责任编辑 刘 舸)

Modeling and Validation on Circumferential Velocity Ratio of Receiver Hole

ZHANG Jian－chao1，2，WANG Suo－fang1，2，WANG Chun－feng1，2，3，XU Hao1，2，MA Li1，2
(1.Jiangsu Province Key Laboratory of Aerospace Power Systems，Nanjing 210016，China; 2.School of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China;3.Jiangling Motots Co.Ltd，Nanchang 330001，China)

Simplified pre－swirl system and flow field nearby receiver hole under typical conditions were analyzed.Based on the consequences，circumferential velocity ratio model of receiver hole was constructed.CFD analysis was carried out through a series of typical conditions.Result of comparing to CFD data demonstrates the model prediction is effective.Current study results show that:based on flow pattern inside receiver hole，this area was divided into 3 regions，influencing factors including swirl ratio，length－radius ratio and attack angle，the model to predict circumferential velocity ratio was proved to be enough accuracy.In contrast to the original receiver hole component model，that modified by circumferential velocity ratio makes better coincide with CFD data.

pre－swirl;receiver;circumferential velocity ratio;one－dimensional flow path

V231.3

A

1674－8425(2014)07－0043－07

10.3969/j.issn.1674－8425(z).2014.07.010

2014－01－09

张建超(1984—)，男，河南漯河人，博士研究生，主要从事发动机内部流动与冷却方面的研究。

张建超，王锁芳，王春凤，等.接受孔元件的周向速度系数模型与验证［J］.重庆理工大学学报:自然科学版，2014(7):43－49.

format:ZHANG Jian－chao，WANG Suo－fang，WANG Chun－feng，et al.Modeling and Validation on Circumferential Velocity Ratio of Receiver Hole［J］.Journal of Chongqing University of Technology:Natural Science，2014 (7):43－49.