高频数据下基于VaR模型的我国金融市场研究
2014-06-27魏正元霍艳李文
魏正元,霍艳,李文
(重庆理工大学数学与统计学院,重庆 400054)
高频数据下基于VaR模型的我国金融市场研究
魏正元,霍艳,李文
(重庆理工大学数学与统计学院,重庆 400054)
基于“国内外市场间的异构性质”和“传统的风险模型是否能有效地应用于今天的高频金融市场”的考虑,设计了历史模拟法、蒙特卡洛模拟法和极值理论方法,依次对深市的“宝安地产、长江证券”与沪市的“沪深300”3支个股进行对比研究,并进行失败率检验。结果发现:国内两大金融市场并无明显差异;历史模拟法和蒙特卡洛模拟法并不能对风险值进行有效的估计;极值理论可以对国内高频金融市场进行有效的风险度量。同时实验的结果也反向论证了模型适用的前提条件的重要性。
历史模拟法;蒙特卡洛模拟法;在值风险(VaR);极值理论
由于金融市场的信息对证券市场价格运动过程的影响是连续性的,所以数据采集的离散程度决定了获取信息的程度。然而,随着存储和计算技术的快速发展,各数据库可以采集到以小时、分钟或秒为单位的频率越来越高的数据,即高频数据。在研究高频金融数据的具体应用时,对数据的正确认识和使用往往以数据本身的统计特征为基本前提。由于金融高频数据与低频数据(即以日、周、月等为采集频率的数据)间特性的差异,使先前一些基于低频数据上的“短期价格波动服从高斯随机游程的古典经济假设”、“不同方法的风险估计模型”等理论都不再适用。因此,对高频金融数据的度量与应用日益得到国内外更多学者的高度重视,其中代表人物是Andersen和Engle。
本文基于金融市场中微观结构理论的视角,采集国内流动性高的5 min高频交易金融资产价格数据,设计最优的抽样方案,并基于上述模型做实证分析。利用参数方法(历史模拟法和蒙特卡洛模拟法)和非参方法(极值理论)对在险价值(VaR)进行估计,比较沪市的“沪深300”和深市的“长江证券、宝安地产”的在值风险(VaR)走势,观测我国2个金融市场的异同性。
1 理论与模型
1VaR模型的定义
在险价值(VaR)是指在市场的正常波动下,某一金融资产可能发生的最大损失。数学描述是在给定的置信度水平下,某一金融资产在未来特定持有期内的最大可能损失,表达式为
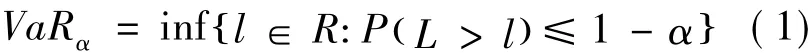
其中:α是置信水平(95%或99%);L是在持有期Δt内的资产损失。由式(1)可知:要确定金融机构的在险价值(VaR)模型,首先要确定持有期间的长短、置信区间的大小、观察期间3个指标。本文对3个指标的选取依据如下:
1)持有期间的长短。即确定在某时间段内的持有资产的最大损失值。本文选择的持有期以每日为周期,原因如下:首先,因为5 min的高频数据具有“包含的市场信息量和市场微观结构噪声影响最小”达到均衡的优越性质;其次,“持有期的选择依据所持有资产的特点来确定,对于流动性很强的交易往往以每日为周期计算在险价值(VaR)”。
2)置信区间的大小。置信区间的选择在一定程度上反映的是金融机构对风险的不同偏好。较大的置信水平意味着对风险比较厌恶,希望可以达到把握性较大的预测结果,使模型对于极端事件的预测准确性较高。基于本文的研究目的,选取95%的置信水平进行预测。
3)观测期间。针对给定持有期限的回报的波动性和关联性考察的整体时间长度,是整个数据选取的时间范围。例如选择对某资产组合在未来6个月或是1年的观察期间内,考察其每周回报率的波动性(风险)。这种选择要在历史数据的可能性和市场发生结构性变化的危险之间进行权衡。为克服商业循环等周期性变化的影响,历史数据越长越好,但是时间越长,收购兼并等市场结构性变化的可能性越大,历史数据因而越难以反映现实和未来的情况。巴塞尔银行监管委员会目前要求的观察期间为1年,因此本文选择的观测期间是2013年1月到12月。
1.2 历史模拟法
Butler和Schachter[1]提出了基于核估计的历史模拟法来估计VaR值,适用于观测周期较长的情况。Cabedo和Moya[2]提出一般的历史模拟法,它是通过历史模拟法基于误差项对VaR值进行估计。以上2种方法都给不同时期的观测值赋予了相同的权重,即默认组合的历史收益率是独立同分布的。近年来,Asfaha[3]通过对数据的处理,结合bootstrap方法对历史模拟法进行了改进。陈玉峰、孙洪祥[4]在应用历史模拟法计算在值风险(VaR)的基础上,采取增加权重和波动率等提高在值风险(VaR)的估计精度。但历史模拟法的原理之一是:假定以后事件的发生是之前事件发生的重复,并没有考虑到之前事件没有发生的情况,也忽略了由于数据采集频率低、数据不足而导致的对在值风险(VaR)的不精确估计。
历史模拟法原理:根据观测计算得到的股市收益率变化值模拟股市的未来损益分布,再通过分位数给出一定置信度下的在险价值(VaR)估计。
历史模拟法的优点:概念直观,不需要对资产收益的分布特征做假设,易操作。缺点:假定未来的概率分布与金融收益的历史数据的概率分布完全一致,显然这一假定违背了金融波动的易变性;历史模拟法需要大量的观测数据(通常至少为1 500个),否则会严重地低估风险。
1.3 蒙特卡洛模拟法
蒙特卡洛模拟法是一种随机模拟法,它用通过观测值的历史波动产生观测值的未来波动的可能路径,同时克服了历史模拟法正态性假设的缺陷。王春峰、万海辉提出了“马尔科夫链蒙特卡洛模拟法”来估计在值风险(VaR)。
蒙特卡洛法原理:根据观测数据本身的特征来模拟一系列符合要求的伪随机数,对这些伪随机数通过历史模拟过程得到在险价值(VaR)。
蒙特卡洛模拟法的优点:不需要对金融收益的历史数据的概率分布做假设,可以较好地处理非线性和厚尾的问题。缺点:计算量大,对随机模型存在依赖,若模型有缺陷,会导致在险价值(VaR)严重失真。
1.4 极值理论
传统的非参数风险度量方法往往忽略了分布的尾部信息,极值理论可以表现出良好的尾部时间预测能力。longin[5]通过极值理论对S&P500的多头和空头头寸进行在值风险(VaR)估计,通过与置信水平为5%的正态分布假设下的在值风险(VaR)相比,发现其具有更好的精确度。Ramazan 和Faruk[6]应用极值理论方法估计9个不同市场的股票在值风险(VaR),发现在值风险(VaR)的估计精度随着置信水平的升高而增加。
无论是历史模拟法还是蒙特卡洛模拟法,得到的在险价值(VaR)都是基准值,而未能考虑尾部分布,而极值理论将研究重心放到了收益的尾部而非整个分布。
原理:将收益率分成多个子区间,然后选取各个子区间的最大和最小值,得到极值序列,依据最值服从广义极值分布(GEV)理论进行建模。缺点:适用于收益率集中的最值,会损失较多的尾部信息。

2 实证分析
主要针对“不同的风险度量模型在中国市场的表现差异”进行实证分析,分别通过历史模拟法、蒙特卡洛模拟法、极值方法对在值风险(VaR)进行估计。通过R软件绘制出不同条件下2013年的实时在值风险,使风险值可视化。通过实证分析,对比国内2个金融市场的异同。
2.1 历史模拟法
首先,根据股票每5 min的交易数据计算第d 天t时刻的股票收益率Rd,t=ln( Pd,(t+1)Pd,t);将每天的收益率按升序排列,根据损益分布计算出置信度分位数为95%的VaR值。
其次,本文中每支股每天有48个收益率观测值,第24观测值的最大损失值即为95%的置信度所对应的分位数。2013年来自2个市场的3支股票238天的在值风险(VaR)如图1所示。
由图1可以发现(VaR的负值情况代表收益):实际的损失值几乎全部大于VaR值的个数,即所估计的在值风险(VaR)估计几乎全部失效。以下采用Kupiec失败率检验方法对在值风险(VaR)的有效性进行检验,结果见表1。
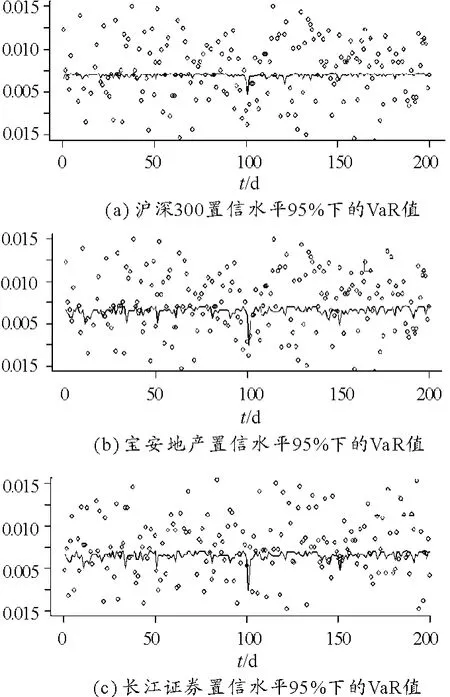
图1 2013年3支股票238天的在值风险(VaR)
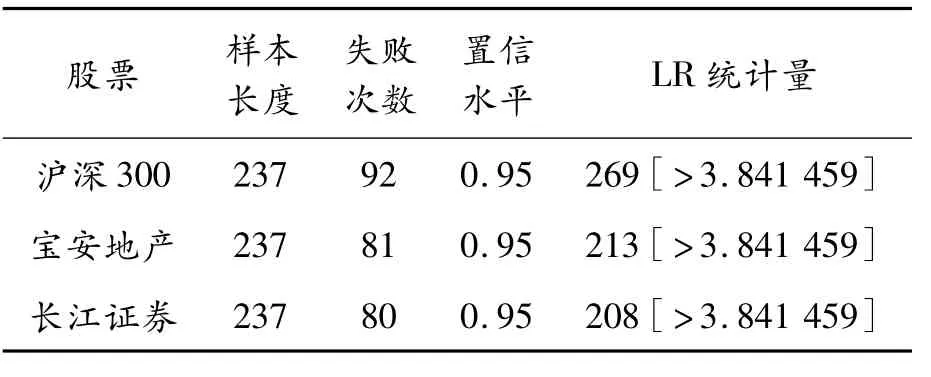
表1 对模拟结果的Kupiec失败率检验
由表1知:经过Kupiec失败率检验,发现在95%的置信水平下LR的值大于临界值。因此,可以初步认定对于以上3支样本,历史模拟法并没有完全通过Kupiec失败率检验,没能对3支样本的风险值做出有效的度量。
2.2 蒙特卡洛模拟法
Shapiro-Wilk检验是用顺序量W检验分布的正态性,检验样本容量为3~5 000,经研究Shapiro-Wilk效果最高。
首先,通过每天观测值的直方图观察历史数据的分布特征,判断是否符合正态分布。本文选取“沪深300”进行Shapiro-Wilk检验(表2),判断“沪深300”是否符合正态分布。结果显示W统计量的值均接近于0,前2个交易日的p值均大于0.05,第5个交易日的p小于0.05,即前两日的数据符合正态分布,第5日的数据并不符合正态分布,即本文沪深300的237个日内交易数据并非全部符合正态分布,但目的之一是“利用高频数据选取非参数方法对国内两大金融市场进行比较分析”,所以下文仅基于蒙特卡洛方法进行在险值(VaR)计算。一者对结果进行Kupiec失败率检验,从反面论证正态性条件对蒙特卡洛方法计算在险值的必要性;一者应用其结果与本文其他的方法所计算的在险值进行量化比较,给出定性的分析,判断国内两大金融市场的异同性,寻找最合适在险值模型。
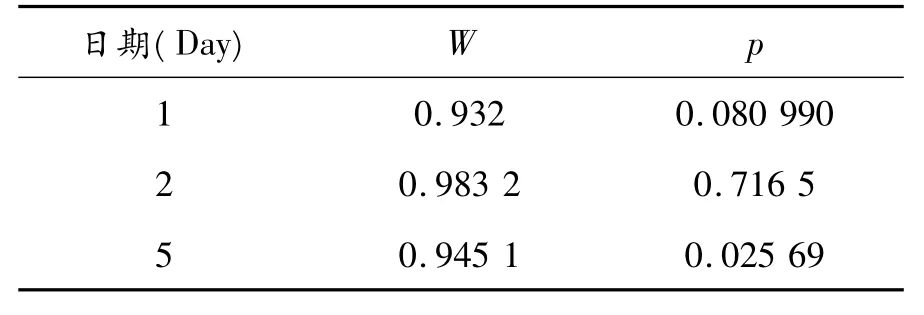
表2 对‘沪深300’的Shapiro-Wilk检验
其次,通过R语言函数rnorm()产生每天相应的10 000个随机数。通过历史模拟法对以上随机数进行分析,得到2013年来自2个市场的4支股票238天的在险值(VaR),如图2所示。
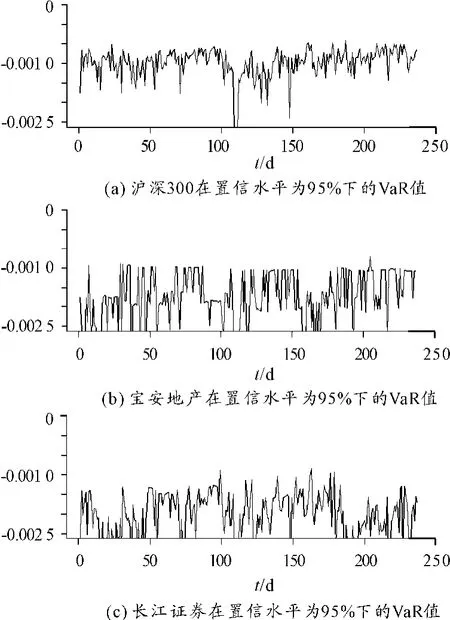
图2 蒙特卡洛模拟下的在值风险(VaR)
图2表明:就方法而言,采用蒙特卡罗模拟法计算而得的在值风险要小于历史模拟法计算得到的在值风险;就市场而言,初步识别国内2个市场并没有极大的差异性。通过Kupiec失败率检验法对蒙特卡罗模拟法的有效性进行检验,结果见表3。
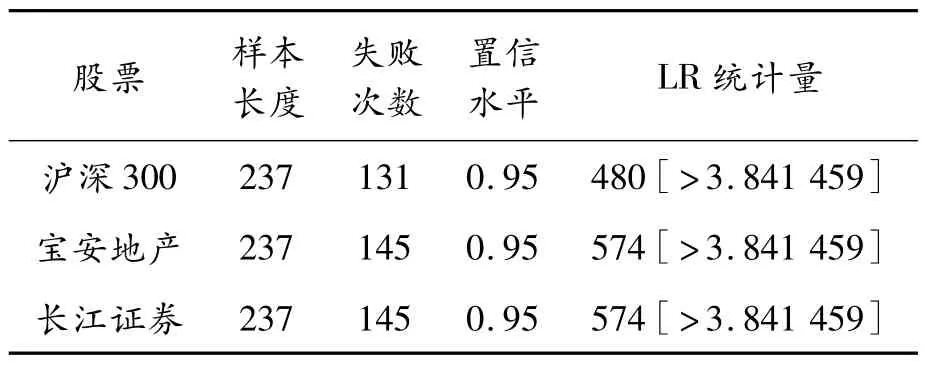
表3 对蒙特卡洛模拟结果的Kupiec失败率检验
结果表明:蒙特卡洛模拟法对3支股票在险值的估计的失败次数均大于历史模拟法所得在险值的失败次数,从侧面证实了采用蒙特卡罗模拟进行在险值(VaR)估计时正态性条件的必要性。
2.3 极值理论法
无论是应用历史模拟法还是蒙特卡洛模拟法,得到的VaR值都是基准值,没能考虑尾部分布,而极值理论将研究重心放到了收益的尾部而非整个分布。
原理:首先假设Rd,t的值是彼此独立且来自于同一分布FXn(x)=1-(1-FR(x))n,因此易知FX∞=0,即当n→∞Xn的极限分布是收敛的,设存在规模参数αn>0,位置参数βn>0使(Xn-βn)αn=X*为标准化且非收敛,依据Gumbel的定理:标准化后的极值存在的极限分布形式为:

综合以上分布知:所有不同的收益分布有相同的极限分布(区别仅在于参数不同)。
首先,根据极大似然估计法估计广义极值分布的参数值(见表4),从而进一步估计极值的渐近分布。
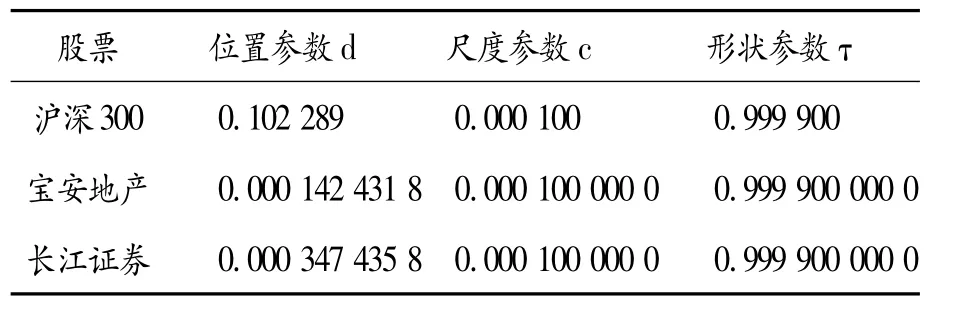
表4 广义极值分布的参数估计值
其次,依据极大值序列的广义极值分布计算得到
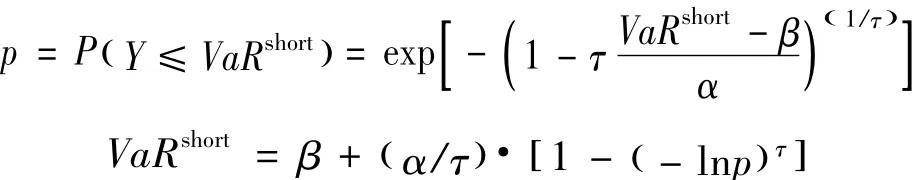
最后,计算出3支股票的在值风险(VaR),如图3所示。
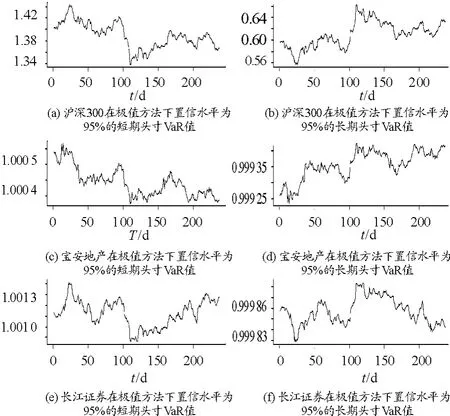
图3 极值理论下的在值风险(VaR)
由图3可见:用极值理论计算得出的在值风险(VaR)要远远大于用蒙特卡洛和历史模拟法计算得出的在值风险(VaR)。因此,如果在银行内部采用“极值理论”计算在险值,则会提高银行风险管理的资本,进一步从侧面证实了极值方法在银行界采用较少的原因。下面通过Kupiec失败率检验方法对长期头寸VaR值和短期头寸VaR值的有效行分别进行检验,结果见表5。
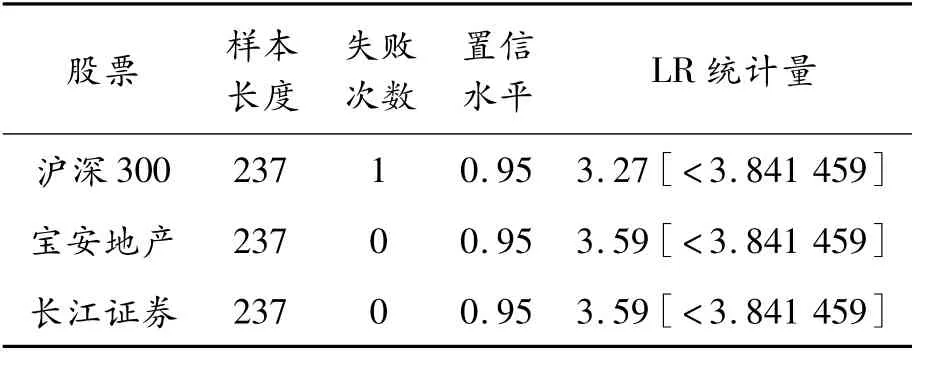
表5 对极值理论结果的Kupiec失败率检验
检验结果显示:在95%的置信水平下LR统计量大于卡方统计量的临界值。说明:①对同一支股票而言,不论是长期头寸还是短期头寸,它们的失败次数是一致的;②同蒙特卡洛和历史模拟法相比,极值理论计算所得的VaR值通过了Kupiec失败率检验,初步说明与历史模拟法和蒙特卡洛模拟法相比,应用极值理论可以利用高频数据对我国市场的在值风险(VaR)进行有效的估计。
3 结束语
为了判别国内金融市场间是否存在异构型,本文选取了国内沪深两大金融市场2013年的“沪深300”、“宝安地产”和“长江证券”的5 min高频数据作为研究对象,选取经典的历史模拟法、蒙特卡洛模拟法和极值理论依次对3支股票的在值风险进行预测,并通过Kupiec失败率检验对国内金融市场异构性做出判断。初步得到以下结果:历史模拟法并不能很有效地应用于高频金融数据的国内市场;为了考查国内市场高频数据的正态性,采用Shapiro-Wilk检验方法,依次对每天的历史数据进行分析,发现全年每天的交易数据并不能全部显示出正态性,从而初步断定蒙特卡洛模拟法对VaR值得估计会失效,Kupiec失败率检验的结果验证了这一断定。为了判定是否数据存有后尾特性,本文在蒙特卡洛模拟之后应用了极值理论对3支个股数据进行分析。结果显示:通过极值理论计算的VaR值能够大部分通过失败率检验,可有效地对国内市场的在值风险进行度量。
[1]Butler J S,Schachter B.Estimating value-at-risk with a precision measure by combining kernel estimation with historical simulation[J].Review of Derivatives Research. Springer,1998,1(4):371-390.
[2]David J,Moya.Estimating oil price“Value at Risk”using the historical simulation approach[J].Energy Economics,2003,25(3):239-253.
[3]Asfaha T,Desmond A F,Hailu G.Statistical Evaluation of Value at Risk Models for Estimating Agricultural Risk [J].Journal of Statistical and Econometric Methods,2014,3(1):13-34.
[4]陈玉峰,孙洪祥,温巧燕.基于历史模拟法的VaR计算及其优化[J].中国科技论文在线精品论文,2011,4 (13):1231-1237.
[5]Longin F M,From value at risk to stress testing:The extreme value approach[J].Journal of Banking and Finance,2000,24(7):1097-1103.
[6]Genay R,Seluk F.Extreme value theory and value-atrisk:relative performance in emerging markets[J].International Journal of Forecasting,2004,20(2):287-303.
(责任编辑 刘舸)
Study on the High Frequency Data of the Financial Market in China by Using the VaR Method
WEI Zheng-yuan,HUO Yan,LI Wen
(School of Mathematics and Statistics,
C
hongqing University of Technology,Chongqing 400054,China)
With the rapid development of storage and computing technology,high frequency data with real-time transaction acquisition market become true.In order to study the relations between the two major domestic financial market,we choose two stocks named as“Changjian zhengquan”and“Bao’an dichan”from Shanghai market and“Hushen 300”from Shenzhen market.Monte Carlo simulation method,extreme value and historical simulation method will be selected to analysis each of the above three stock,then tested the failure rate.The results show that there is no remarkable difference between Chinese two financial market;the historical simulation method and Monte Carlo simulation method is not effective for risk estimation;extreme value theory can effectively measure the risk of domestic high-frequency Market.
historical simulation method;Monte Carlo simulation method;value at risk(VaR);extreme value theory
O21
A
1674-8425(2014)08-0126-06
10.3969/j.issn.1674-8425(z).2014.08.026
2014-03-28
重庆市自然科学基金资助项目(cstc2012jjA00018);重庆市教委科学技术研究项目(KJ130810);重庆市教委高教研究项目(1203053)
魏正元(1975—),男,博士,副教授,主要从事应用概率统计、金融统计、金融数学研究。
魏正元,霍艳,李文.高频数据下基于VaR模型的我国金融市场研究[J].重庆理工大学学报:自然科学版,2014(8):126-131.
format:WEI Zheng-yuan,HUO Yan,LI Wen.Study on the High Frequency Data of the Financial Market in China by Using the VaR Method[J].Journal of Chongqing University of Technology:Natural Science,2014(8): 126-131.
