基于复杂网络的三板市场结构及投资组合研究
2014-06-27任达夏小卿
任达,夏小卿
(天津大学管理与经济学部,天津 300072)
基于复杂网络的三板市场结构及投资组合研究
任达,夏小卿
(天津大学管理与经济学部,天津 300072)
以三板市场股票为研究对象,运用复杂网络理论对三板市场进行分析,并与主板市场进行对比。研究发现三板市场股票价格相关性网络具有较小的聚集系数以及较短的特征路径长度,结构偏向于随机网络,复杂性特征不如沪深股市网络明显。利用GN算法对三板市场股票价格相关性网络进行社团划分,并基于此构建股票投资组合,此结果对投资者进行三板市场分散投资具有较好的指导意义。
三板市场;复杂网络;阈值法;社团;投资组合
三板市场最初是指证券公司代办股份转让系统,是为原STAQ和NET系统公司和证券交易所退市公司的股份转让提供报价服务,被后来的学者认为是“旧三板”或称为“深三板”市场。2006年证券业协会对三板市场进行扩容,现在的三板市场还包括中关村科技园非上市股份有限公司股份报价转让系统。本文所指的三板市场是指在原证券公司代办股份转让系统扩容以后,将中关村科技园区非上市股份有限公司也纳入进来的代办股份转让系统,全称为证券公司代办股份转让系统及中关村科技园区非上市股份有限公司股份报价转让系统,即包括深三板市场和新三板市场两部分。
1 文献综述
关于我国三板市场的研究,周茂清、尹中立[1]从“新三板”市场的形成、功能及其发展趋势方面对三板市场进行了概述。吴振华等[2]围绕新三板及其挂牌条件与程序等方面进行了探讨。刘晶、何以[3-4]对三板市场信息披露制度、交易制度进行了评价并提出进一步完善的建议。可以发现:三板市场研究多数集中于其制度政策等方面的定性分析,而对于三板市场的内部结构并没有从定量角度分析其市场具有的内在性质特征。
三板市场作为一个证券市场,其本身是一个包含大量信息的复杂系统。复杂网络是复杂系统的抽象,它舍弃了小尺度上的细节作用而更关心其本质行为。事实上,三板市场网络本身的拓扑结构具有其内在、本质的特性,一旦确定下来,必然对三板市场网络的性能产生深刻的影响。这就为研究三板市场内部结构特性提供了一个途径[5-6]。
近年来,运用复杂网络理论研究证券市场逐步成为国内外理论界研究的热点,相关文献主要集中在股票关联网络的基本统计性质和对网络内在社团结构信息的挖掘两方面研究。一方面,Mantegna[7]首次根据股票价格数据构建了股票关联网络,运用该股票关联网络对标准普尔500只股票进行了统计性质分析,并激发了后续研究;庄新田、马兴福等[8-9]基于相关系数分别构建了上海证券市场及中小企业板股票市场网络,研究了其拓扑统计特性。另一方面,Son等[10]提出了一种用于划分加权网和非加权网的社团结构的方法,并用于研究纽约证券交易所的137支股票网络。黄玮强、王娟等[11-12]分别利用派系聚类和Newman算法对我国沪深股市网络成功地划分出社团结构。股票关联网络内在社团结构信息有助于从价格波动相关性方面了解股票之间的关联关系,对股票组合投资、风险管理具有重要的意义。对于三板市场,由于其交易不活跃,上市公司信息披露制度不完善,导致三板市场的投资决策尤其困难;同时三板市场(尤其是新三板市场)股票的行业特征不明显,使得基于行业板块构建投资组合的传统策略具有局限性。而利用复杂网络社团结构理论对三板市场股票价格相关性网络进行社团划分,则为三板市场投资者进行分散投资提供了一种独特的视角和方法。
本文拟利用复杂网络的理论和研究方法,以三板市场股票为研究目标,运用阈值法构建相应的股票关联网络。分析网络的统计性质和社团结构,进而探索三板市场网络本身所具有的内在性质,并通过研究复杂网络社团划分理论在三板市场的应用,从而帮助投资者在三板市场进行投资决策,分散投资风险。
2 股票关联网络构建方法
2.1 数据选取
为建立三板市场的网络模型,搜集2009年1月1日~2012年12月31日在三板市场上市的股票,包括证券代办股份转让系统原有股票和中关村科技园区非上市股份有限公司,共选取三板市场中上市交易数据较多的股票78只。其中,在深三板市场上市股票56只,在新三板上市的股票22只。由于三板市场不同股票的交易周期也不同,分为一周交易1天、3天和5天,考虑到时间周期的一致性,以周间隔为时间间隔计算股票价格波动相关系数。
2.2 三板市场复杂网络建模
令Pi(t)为第i只股票t时刻的收盘价格,则定义股票i的对数收益为
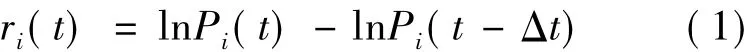
Δt为计算收益率的时间周期,在本文中为周间隔。
相关系数衡量2个变量之间相关关系的密切程度,利用收益率序列计算的相关系数可表示2个股票在观测时间内价格波动的相互影响关系,其中Pearson相关系数应用最为广泛,但是值得注意的是它对数据有正太性要求。
由于深三板、新三板数据样本个数分别为56 和22,因此分别利用D检验(适用于样本数≥50)、W检验(适用于样本数≤50)对深三板、新三板市场股票数据进行正太性检验。应用SPSS对D值、W值统计量进行计算,结果显示数据服从正态分布,符合皮尔逊相关系数要求。因此本文采用运用最为广泛的Pearson相关系数,定义为

其中:ri、rj分别代表股票i、j的收益率序列,〈〉为变量的期望值。如果两只股票完全正(负)相关,则Pij=±1;如果两只股票完全无关,则Pij=0。计算三板市场中任意两只股票的收益率相关系数,得出相关系数矩阵P,P为实对称矩阵。
首先根据公式(1)、(2)计算深三板市场与新三板市场中股票相关系数及其概率分布图,如图1所示。深三板市场中股票相关系数均为正数,多数集中在0.4左右,均值为0.44;而新三板市场中股票相关系数正负均有出现,比例相当,均值在0左右。上述结果说明:深三板市场和新三板市场之间股票的波动特征存在明显差异。基于此,本文将三板市场分为深三板市场和新三板市场两部分进行复杂网络建模并分析。
本文选取阈值法构建三板市场网络,即以三板市场股票为节点,基于股票相关系数矩阵P建立连边,当且仅当两只股票相关系数Pij大于或等于指定阈值θ时,节点i和j之间有边相连,从而构建一个无向无权股票价格相关性网络。
选取不同的阈值θ会构建出不同的网络,目前主要采用边权重过滤技术作为阈值选择的标准。GARAS等指出:在原始金融网络中强连边(意义明显的连边)与弱连边(意义不明显的连边)同时存在,逐步移除网络中的弱连边,网络中理想的结构就逐渐呈现出来,这就是“边权重过滤技术”[13]。

图1 深三板市场和新三板市场股票相关系数描述统计图
在构建网络时,按照相关系数排名由高到低逐步在网络中添加连边,参数s表示网络中实际存在的边数与完全图中存在的边数之比。不同阶段生成的网络可由s值来表示,s与阈值θ之间存在一一对应关系,如表1所示。依据边权重过滤技术,通过选取合适的s值,逐步删除网络中的弱连边,从而使得网络具有最明显的连通性、聚集性等结构特征。这里分别选择网络最大连通子图的节点个数与网络的平均聚类系数来反映网络的连通性和聚集性,如图2所示。
由图2(a)、(b)可知:随着s的逐渐增大,最大连通子图的节点个数和相应的聚类系数呈现逐步增加的趋势,当s增加到0.81后,最大连通子图的节点个数和相应的聚类系数值趋于平稳。因此,对深三板市场,网络的最佳参数值s为0.812,对应的最佳阈值θ为0.5。对图2(c)、(d)作同样分析,其最大连通子图的节点个数和相应的聚类系数在s增加到0.12后,增加的趋势变缓并趋于稳定。因此,新三板市场网络最佳参数值s为0.12,对应的最佳阈值θ为0.2。

表1 阈值θ-s值对照表
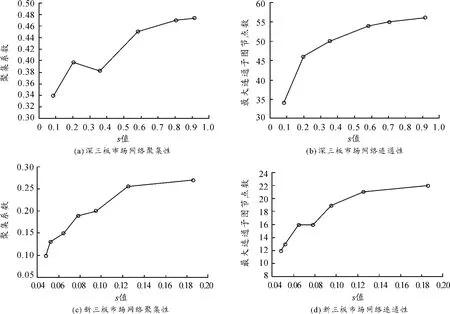
图2 边权重过滤技术分析三板市场网络结构
3 深三板和新三板市场网络统计性质分析
3.1 网络统计性质
定义1聚集系数C。描述了网络的紧密程度。假设节点i有ki个邻接节点,则这些邻接节点之间实际存在的连边数Ei与总的可能的边数之比定义为节点i的聚集系数Ci,即

整个网络聚集系数C是所有节点i聚集系数Ci的平均值。C的取值区间为[0,1],主要反映网络的局部性质,与网络的局部聚集水平正相关。
定义2特征路径长度L。2个节点之间的距离dij被定义为连接这2个节点的最短路径上所包含的边的数目,网络的特征路径长度为任意2个节点之间的距离的平均值,表示为

L表征了网络上要素传递的便捷水平,主要反映网络的全局特性,与网络上要素传递的便捷水平负相关。
小世界效应:不同的网络有各自不同的统计性质。规则网络具有大的聚集系数Creg和特征路径长度Lreg,随机网络具有小的聚集系数Cran和特征路径长度Lran,而真实网络一般介于两者之间,同时具有大的聚集系数集系数Creal和小的特征路径长度Lreal,如果一个网络满足

则称其具有小世界效应。定义3度分布。一个节点的度为该节点连接的所有连边的总和。网络的度分布即为网络中节点的度的概率分布或频率分布,记为P(k)。
无标度特性:如果一个网络的度分布在双对数坐标下呈现幂率分布特性,即P(k)∝k-γ,则称这种网络具有无标度特性,γ为幂率系数。无标度网络特点为:大部分节点度较低,而有极少的节点度很高,为网络中的关键节点。
3.2 三板市场网络统计性质分析
在指定阈值θ=0.5及θ=0.2时,分别对深三板市场和新三板市场网络的统计性质进行分析。
3.2.1 特征路径长度和聚集系数
通过复杂网络软件ucinet 6.0计算深三板市场和新三板市场网络的特征路径长度和聚集系数。表2显示深三板、新三板市场及同等规模下(相同节点数与平均度)规则网络与随机网络的统计特征。

表2 三板市场网络的统计特征
其中(Cran,Lran)、(Creal,Lreal)、(Creg,Lreg)分别代表真实网络、随机网络、规则网络的聚集系数与特征路径长度。
从表1中可以看出:对深三板市场来说,Creal≈Cran,Lreal≈Lran,即其聚集系数和路径长度与随机网络的特征接近,并不满足小世界效应的特征。这说明深三板市场网络本身偏向于随机网络。在深三板市场中,任意股票的价格波动可以迅速地在整个市场中产生影响,然而其聚集系数很低,说明价格波动对于局部(相邻股票集团)的影响并不是很剧烈,没有价格波动在集团内部传播更为剧烈的局部效应。对新三板市场来说,Creal>Cran,Lreal≤Lran,其聚集系数略大于随机网络聚集系数,但平均路径长度远远小于随机网络的值,同样不满足小世界特征。其特点是:股票价格波动在整个新三板市场内得到更为迅捷的传播,甚至比随机网络的传播速度更快,而股价波动在局部范围内的传播仍然并不显著。
3.2.2 度分布情况
分别在指定的阈值θ下,研究两市场网络的度分布情况。图3表示的是在指定阈值下深三板与新三板证券市场网络节点的度分布。
由图3可以看出:深三板市场和新三板市场网络度分布的拟合优度很低,表明网络节点度不服从幂律分布,三板市场的网络结构不具有无标度特性,即三板市场网络中并没有度很大的关键节点,在市场中股票之间影响力水平相近;沪深股市网络的幂率系数在2~3,具有明显的无标度特征,即市场中存在少量关键股票,其价格波动在市场中对其他股票具有重大影响,通过对这些股票的重点监控,能够有效地控制股市稳定。相比而言,三板市场无法识别出相对重要的股票,体现了三板市场监控的困难性。
综上所述,深三板市场与新三板市场网络不具有小世界效应与无标度特性,与沪深股市网络相比,三板市场网络的复杂性特征不明显,股票价格波动倾向于全局传播,局部范围内规律性不强。三板市场的规模小,股票交易不活跃,股票之间关联性不强等抑制了其复杂性特征的涌现,也反映了三板市场内部结构的不成熟、不健全。

图3 深三板和新三板市场网络度分布双对数坐标图
4 三板市场网络的社团结构
4.1 三板市场网络社团划分方法
三板市场中股票之间的关联网络结构没有明显特征,股票价格波动之间规律不明显,随意性更强,使得投资者在三板市场上的投资相比于沪深股市参考信息更少,具有更大的风险。因此,将三板市场股票价格相关性网络分割成不同的社团是极具投资参考价值的。股票价格相关性网络中的社团就好比投资者按基本面区分的“板块”,由于证券价格相关性网络的边是价格相关性,因此投资者选择投资组合时参考证券价格相关性网络中的“社团”能更好地进行组合投资以分散投资风险。
本文采用GN算法进行三板市场网络社团划分。2002年,Girvan和Newman首次提出GN算法[14],其基本思想是:按某种规则,不断地从网络中移边,从而逐步将网络划分成不同的社团结构,但是不能明确给出一个最佳的社团结构。为此,Newman等[15]首先提出模块度评价函数的概念。它是用来衡量社团结构划分好坏的重要测度,模块度Q值范围为0~1,Q值越大,说明社团结构越明显。因此,在利用GN算法进行社团划分时,可以进一步借助Q值得到最优社团结构。
这里对指定阈值下的深三板市场和新三板市场分别进行社团划分。考虑到应该把价格波动相关性接近的证券归入一个社团,因此在构建网络时分为2种网络:股票价格正相关时有边相连的正相关网络和股票价格负相关时有边相连的负相关网络。由于深三板市场内相关系数全为正,对深三板市场,取阈值θ=0.5;而对新三板市场,取阈值θ=±0.2。
4.2 社团划分结果
表3显示了利用GN算法分割指定阈值下深三板市场与新三板市场股票价格相关性网络的结果。2个市场的股票价格相关系数在阈值0.5和±0.2时,都可以成功地将相应的网络分割成不同的社团,对投资者进行组合投资、分散风险具有指导意义。这些社团因为股票价格正相关而聚集在一起,进行组合投资、分散风险时应该在不同的社团之间选择股票。当选择股票价格相关系数小于阈值-0.2时,新三板证券市场股票价格相关性网络可以被成功地分割。这样的社团是因为股票价格负相关而聚集的,进行组合投资、分散风险时应在同一个社团内选择股票。
由理论可知:利用模块度评价函数对社团划分结果进行评价时,应选取Q值最大的结果作为最终的社团划分结果。此时,网络的社团聚类效果最佳。因此,对于深三板市场(θ=0.5)、新三板市场(θ=0.2)、新三板市场(θ=-0.2),应分别将其划分为6、5、5个社团,划分结果分别如图4(a)、(b)、(c)所示。
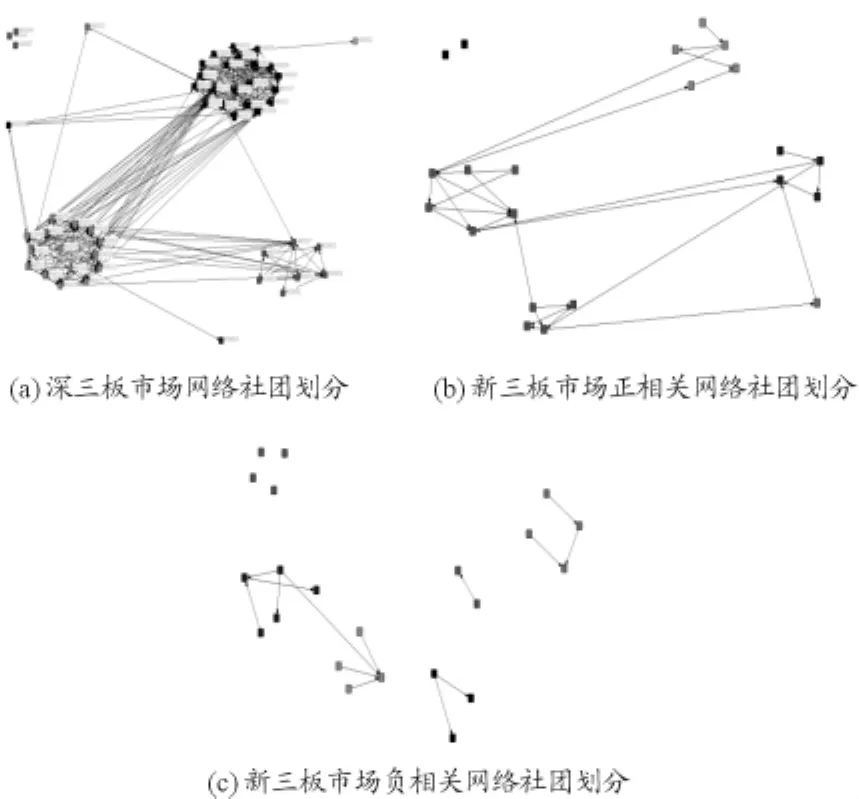
图4 深三板和新三板市场网络社团结构划分
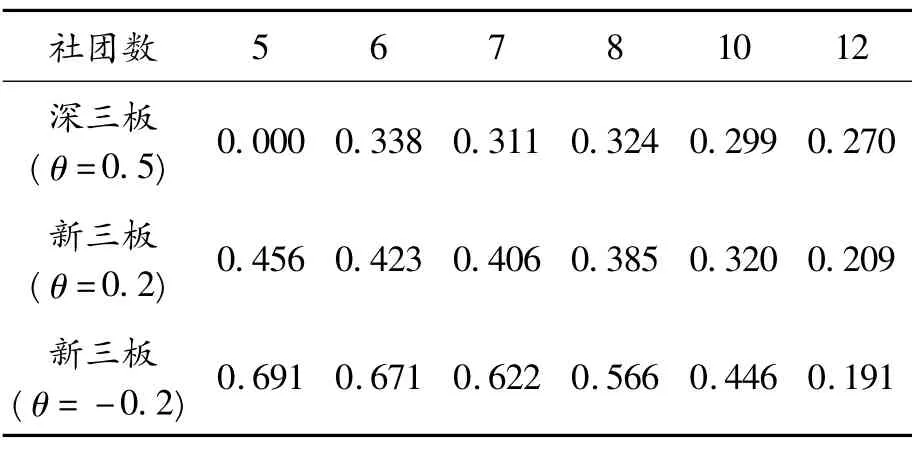
表3 各市场网络社团结构Q值
4.3 投资组合构建
为了检验社团划分对于组合投资的作用,利用社团划分结果,实际构建投资组合,通过对其收益、方差数据的计算,考察所构建的投资组合是否具有风险分散功能。依据图4(a)、(b)、(c)深三板市场及新三板市场网络社团划分结果,选取若干支股票分别构建投资组合P1,P2,P3。数据选择的样本期为2012年1月1日至2012年12月31日,时间跨度一年,数据来源于国泰安数据服务中心。
假设投资者有单位原始资金,不妨设为1。按投资组合W=(w1,w2,…wm)投资到m种股票,这里将投资比例简化为w1=w2=…=wm=1/m≥0(不允许卖空),即对m种股票等比例投资。投资者是理性且厌恶风险的,其目标是选择投资组合策略,能够获得一定的收益,且使风险越小越好。其中依据深三板及新三板市场网络社团划分结果,在构建投资组合时,令组合P1,P2,P3中分别包含6、5、5种股票。
投资组合预期收益率计算:假设每支股票的预期收益率为~ri,组合中各股票所占权重为wi,则投资组合的预期收益率为
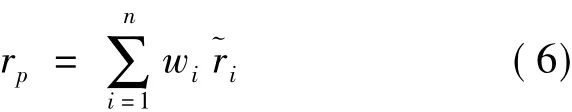
投资组合风险值计算:利用投资组合收益率的标准差来衡量投资的风险程度,当组合中包含股票数量大于等于3时,投资组合的标准差为

根据历史交易数据,得到每支股票的周平均收益率ri,再据此计算每支股票的预期收益率~ri及股票间的收益率协方差cov(i,j),将结果代入公式(6)、(7)计算出投资组合的收益方差。同时作为参照,从深三板、新三板市场中分别按行业划分选取若干支股票组成组合,即从不同行业中选择股票进行投资组合构建,构成对照组,分别计算其不同行业投资组合的收益风险值,并取样10次,取10次平均值,结果见表4。

表4 各市场股票投资组合收益风险值%
利用社团划分方法所构建的投资组合,其风险均小于以不同行业划分进行选取的股票组合,即社团划分理论对于投资组合构建中股票的选取可以提供有效的建议,达到分散投资风险的目的,并且其风险分散的效果比利用不同行业构建的投资组合更加明显。说明对以股票价格相关性相联系的股票市场网络进行社团划分来进行投资组合的构建,比单纯以行业划分构建投资组合能更好地把握住股票之间价格波动的影响,可以更有效地分散风险。进一步在分散风险的基础上,投资者可以继续对组合中各股票投资权重进行最优配置,继而使组合收益达到最高,以实现最优投资。
5 结论
1)三板市场网络具有较小的聚集系数和较短的特征路径长度,结构偏向于随机网络。在此网络中,股票价格的波动能迅速得到传播,并在全局产生影响,但是网络局部紧密程度不高,股票价格波动对其邻居股票的影响效果并不显著,并且在三板市场中各个股票之间差异性小,没有突出的关键股票。
2)对比相对成熟的沪深股市,三板市场网络复杂性特征(如小世界效应、无标度特性)并不明显,各股票之间价格波动相关性的规律难以掌握。这与三板市场的规模小、节点数少、股票交易不活跃等特征相吻合,也反映出了三板市场内部结构的不成熟、不健全。
3)利用GN算法对指定阈值下2个市场网络进行社团划分,均得到较好的社团划分结果。由于股票价格波动相关性网络的边代表价格相关性,因此对此网络进行社团划分比投资者按基本面区分的“板块”更符合投资组合构建的理念,对投资者在风险更大的三板市场分散投资风险、进行组合投资具有指导意义。通过实证检验证实社团划分理论在股票选择、分散风险方面确实具有良好的效果。
[1]马兴福,王红,李园园.基于复杂网络的中小企业板股市网络特性分析[J].计算机技术与发展,2012,22 (4):172-178.
[2]周茂清,尹中立.“新三板”市场的形成、功能及其发展趋势[J].当代经济管理,2011,33(2):75-77.
[3]吴振华,古小刚.关于新三板市场挂牌发行的研究[J].改革与开放,2012(1):35-37.
[4]刘晶.论我国三板市场信息披露制度的完善[J].中国证券期货,2013(2):23-24.
[5]何以.全国联网模式下的三板市场交易制度研究[J].投资研究,2011(5):60-64.
[6]Watts D J,Strogatz S H.Collective Dynamics of“Small World”Networks[J].Nature,1998,393(6684):440 -442.
[7]Albert R,Barabasi A L.StatisticalMechanics of Networks[J].Reviews of Modern Physics,2002,74(1):47 -97.
[8]Mantegna R N.Hierarchical Structure in Financial Markets[J].The European Physical Journal B,1999,11 (1):193-197.
[9]庄新田,闵志锋,陈师阳.上海证券市场的复杂网络特性分析[J].东北大学学报:自然科学版,2007,28(7): 1053-1056.
[10]Son S W,Jeong H,Noh J D.Random field Ising model and community structure in complex networks[J].Eur Phys J B,2006,50(3):431-437.
[11]黄玮强,庄新田,姚爽.中国股票关联网络拓扑性质与聚类结构分析[J].管理科学,2009,21(3):94-103.
[12]王娟,王卫华.基于复杂网络的股票社团化分析[J].武汉理工大学学报:信息与管理工程版,2010,32(5): 829-831.
[13]Garas A,Argyrakis P,Havlina S.The Structural Role of Weak and Strong Links in a Financial Market[J].European Physical Journal B,2008,63(2):265-271.
[14]Newman M E J,Girvan M.Finding and Evaluating Community Structure in Networks[J].Physical Review E,2004,69(2):026113.
[15]Newman M E J.Analysis of Weighted Networks[J]. Physical Review E,2004,70(5):056131.
(责任编辑 刘舸)
Statistical Property and Investment Portfolio Analysis for China’s Third Board Market Based on Complex Networks
REN Da,XIA Xiao-qing
(College of Management&Economics,Tianjin University,Tianjin 300072,China)
We utilize threshold value method to build the third board market network with the stock of the third board market as the research object,and we use complex network theory to analyze the network.To compare the result with the main board market,we find that Chinese third board market network has a small clustering coefficient and short path length which is more like a random network but its complexity character is less obvious than the main board market.Then we use GN algorithm to divide the third market network to several communities and accordingly build stock portfolio to provide guidance of diversity investment for the investors in the third board market.
Chinese third board market;complex network;threshold method;community;investment portfolio
O21;F830
A
1674-8425(2014)08-0106-08
10.3969/j.issn.1674-8425(z).2014.08.022
2014-02-19
国家自然科学基金资助项目(71131007,71373171)
任达(1965—),男,山东莱州人,博士,副教授,主要从事复杂网络与金融市场、金融风险管理、计算实验金融等研究;夏小卿(1988—),女,天津人,硕士研究生,主要从事复杂网络与金融市场、金融风险管理、计算实验金融等研究。
任达,夏小卿.基于复杂网络的三板市场结构及投资组合研究[J].重庆理工大学学报:自然科学版,2014 (8):106-113.
format:REN Da,XIA Xiao-qing.Statistical Property and Investment Portfolio Analysis for China’s Third Board Market Based on Complex Networks[J].Journal of Chongqing University of Technology:Natural Science,2014(8):106-113.
