数码相机量测化检校的二维分步检校方法研究

2014-06-27苏博南阳师范学院环境科学与旅游学院河南南阳473061

长江大学学报(自科版) 2014年22期

苏博 (南阳师范学院环境科学与旅游学院,河南南阳 473061)

苏博 (南阳师范学院环境科学与旅游学院,河南南阳 473061)

为了提高数码相机量测化检校水平,针对目前数码相机量测化检校方法中存在的对物方控制条件要求高、未知参数间相关性强等缺陷,提出了一种新的数码相机检校方法二维分步检校(MSC)方法,即利用微型平面控制场,避开在一个平差过程中同时解算内外方位元素,分步骤独立检校相机的方位元素,避免因同时解算内外方位而产生的未知数之间的相关问题,并减弱像片方位元素对畸变系数解算的影响。实际应用表明,使用该方法能够获得较高的检测精度,因而具有可行性。

数码相机;量测化检校;透视投影变换

数码相机以其通用、方便、廉价的特点,在工程勘测中得到越来越多的应用。然而数码相机缺乏框标和定向设备,像片内方位元素未知,构像畸变差大且未知,这些因素导致其量测精度不高或适用性下降,甚至无法应用。克服上述不足的主要方法,就是对数码相机进行量测化检校。目前常用的数码相机检校方法主要有三维控制光线束检校方法和二维直接线性变换方法[1-4]。三维控制光线束法相机检校方法是基于共线条件方程式,将控制点的物方坐标、内外方位元素以及畸变参数等均视为未知数进行整体平差,同时解算相机的内外方位元素、畸变参数以及待定点物方坐标[5-7]。一般认为该方法解算不稳定,检校参数与实际值有较大的差别。二维直接线性变换方法计算方便,但在检校时仍需引入三维控制。为了解决上述问题,笔者对一种新的数码相机检校方法——二维分步检校(MSC)方法进行了研究。

1 MSC方法基本原理

1.1 相机畸变系数检校

检校相机畸变参数及像主点位置时,微型平面控制场采用刻制在特殊加工平板的方格网,格网中除了存在格网交叉点之外,还存在大量直线。因此,在畸变参数解算的过程中,引入直线参数,以减弱像片方位元素对畸变系数解算的影响,具体方法如下。

1)直线参数的引入对于物方空间直线AB,若影像的误差仅有畸变误差,那么经过畸变改正后,其像方空间构像也应满足同一直线方程:

式中,k为直线斜率;b为直线截距;Δx、Δy分别为x、y方向的畸变差改正数。

当采用上式表达直线时,若直线近似竖直,斜率k会接近无穷大。因此,可将上述方程式改为以θ、ρ为参数的直线方程:

式中,ρ为原点到直线的距离;θ为直线斜距的余角,以x轴为基准,其取值范围为-90°～+90°。在式(2)中加入畸变差改正数可得:

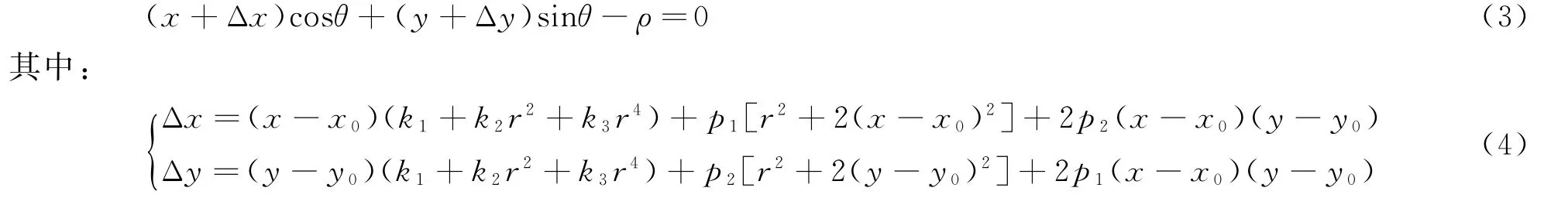
式中,r表示径向半径。

由式(3)和式(4)可知,要求得相机畸变参数和像主点位置(x0,y0),首先要求解出每条直线的直线参数ρ和θ的值。

2)直线参数的解算首先利用透视投影变换对原始像点进行纠正。利用透视变换方程解算出透视变换的8个变换系数,需要无畸变差的像方坐标来参与解算,而没有畸变差的像点坐标仍未求出,因而应选择控制场中心附近且对称分布的4个控制点的坐标参与计算,以抵消畸变的影响,从而获得相对较为准确的解算初值[8-9]。求定8个变换系数后,物方平面与像方平面的位置关系即确定,可利用透视变换解算出控制场点在像平面的投影坐标,最后解出直线参数ρ和θ。

3)畸变参数的解算由于已求出直线参数,式(3)可表示为:

线性化后可得:

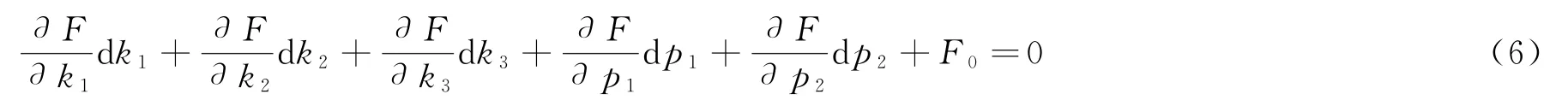
解得畸变参数初值之后,以F为虚拟观测值,列出误差方程式,依据最小二乘原理求得5个畸变系数的最小二乘解。解得畸变参数后,对控制点坐标进行畸变改正,再利用控制点解算投影变换系数及直线参数,如此循环交替,直至2类未知数稳定为止。

1.2 相机主点位置检校

确定畸变参数后,即可进行内方位元素的检校。式(3)可看作是x0、y0的函数,即:

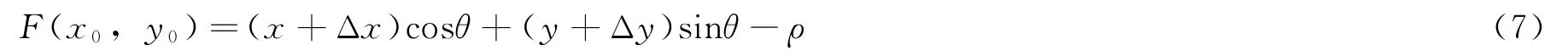
选择控制场中多个对称点,解算x0,y0的最小二乘解。

2 MSC检校控制场的建立

2.1 畸变及像主点参数检校的平面控制场建立及影像获取

MSC检校方法采用的平面控制场为经特殊加工绘制于硬质平板上的方格网,格网为13× 19格,每格100mm×100mm,在格网上布设47个点。为方便像点坐标量测,在格网点上标有黑白对角标志,以提高量测精度。为了保证点坐标不出现负值,以格网中心为原点,并取其坐标为(1000,700),格网行列方向为轴向,建立右手坐标系。平面控制场及控制点点位分布如图1所示。

2.2 主距检校的平面控制场建立及影像获取

用于相机主距检校的平面控制场要求十分简单,即为一精确绘制的格网纸。试验中要求相机严格沿着Z轴方向移动,并要测得Z轴方向的位移作为平差计算的观测值,因此考虑借助于多倍仪实现。多倍仪上的玻璃平板可以精确置平,将相机固定在多倍仪的部件A上,镜头竖直向下。此时相机可在任意空间方向上精确移动,且轴线上均有刻度尺便于准确读数获取平移量。根据水准气泡,调节多倍仪两端升降螺旋使得相机处严格水平。镜头下方严格水平的玻璃平板上平整放置格网纸。影像获取示意如图2所示。将摄影方式设定为对焦无穷远,广角拍摄模式,调节螺旋使控制场的中心成像于像幅中心,控制场平面格网点均匀布满整个像幅。主距检校的平面控制场影像如图3所示。

图1 畸变及像主点参数检校平面控制场及控制点分布图

图3 主距检校的平面控制场影像

3 应用

为检验MSC方法检校结果的可行性,在湖北江坪河水电站某高山峡谷地形处,使用普通数码相机按多摄站方式拍摄多张影像(见图4)。

图4 江坪河电站高山峡谷数码影像示例

该测区宽约200m,高度达150m,拍摄距离约为300m,基线长度约30m。有控制点K2、K3、K4、K6、K10、K12,检查点K1、K5、K7、K8、K9。使用MSC检校所得的相机内方位参数及畸变系数,通过“高山峡谷数码影像测绘与地质填图系统”处理,得到控制点坐标残差及检查点的精度如表1及表2所示。

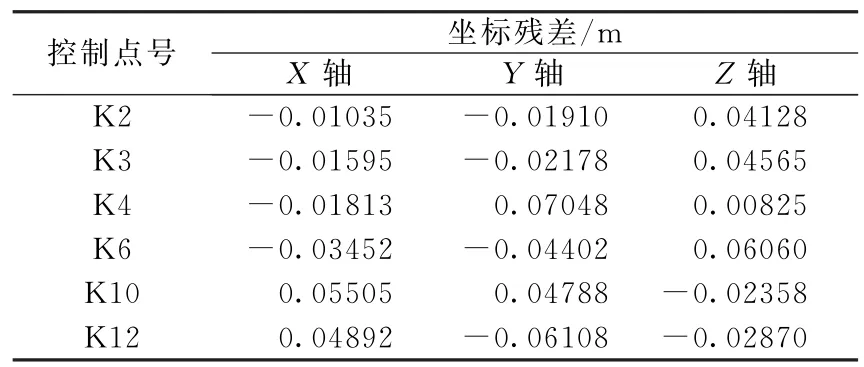
表1 控制点坐标残差

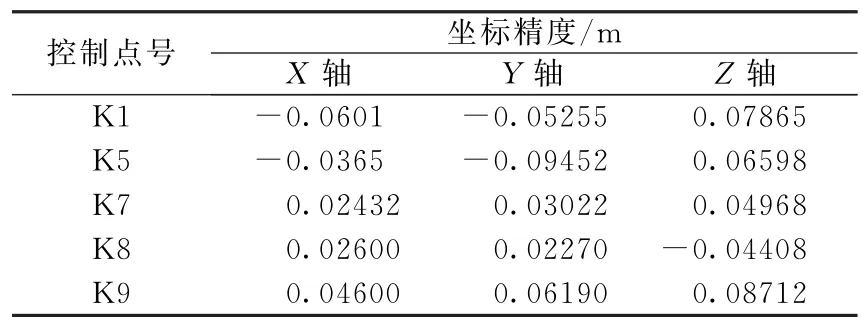
表2 检查点坐标精度

坐标中误差分别为0.0463m(X轴)、0.244m(Y轴)、0.250m(Z轴),相对精度分别为1/6473, 1/1214,1/1164,该结果能够满足工程勘测的精度需求[10]。

4 结语

现行的检校方法通常都使用大型三维控制场,且在检校过程中同时解算相机内外方位元素及畸变参数,内方位与外方位线元素之间相关性不可消除。针对上述不足,提出一种新的数码相机量测化检校方法,即二维分步检校方法。工程应用表明,使用该方法可以解决目前数码相机量测化检校方法中存在的对物方控制条件要求高、未知参数间相关性强等缺陷,具有可行性。

[1]冯文灏.近景摄影测量——物体外形与运动状态的摄影法测定[M].武汉:武汉大学出版社,2004.

[2]徐丽华,谢东海,江万寿.基于预检校的数码相机自检校研究[J].河南理工大学学报,2005,24(2):55-60.

[3]张永军,张祖勋,张剑清.利用二维DLT及光束法平差进行数字摄像机标定[J].武汉大学学报(信息科学版),2002,27(6): 566-571.

[4]张雅楠.平面控制的非量测相机检校方法研究[D].南京:河海大学,2008.

[5]杨林,李浩,闾国年.数码相机的一种检校方法[J].测绘通报,2004,42(8):50-52.

[6]冯文灏.关于近景摄影机检校的几个问题[J].测绘通报[J],2000,38(10):1-3.

[7]苗红杰,赵文吉,刘先林.数码相机检校和摄像测量的部分问题探讨[J].首都师范大学学报(自然科学版),2005,23(3): 117-120.

[8]殷福忠,刘红军.基于DLT方法的非量测数码相机检校研究[J].地理信息世界,2009,7(2):84-87.

[9]陈新玺,李浩,张曼祺.普通数码相机构像畸变差两种检测模型的比较[J].北京测绘,2005,18(4):50-54.

[10]林君建,苍桂华.摄影测量学[M].北京:国防工业出版社,2009.

[编辑] 李启栋

TB852.1