磁源重力技术及其应用
2014-06-27刘春成
吴 兴, 刘春成, 李 军
(1.成都理工大学 地球物理学院,成都 610059;2.中海油研究中心,北京 100027)
0 前言
磁法勘探是所有地球物理方法中发展历史最悠久、应用最广泛的方法之一,在区域地质调查、矿产资源和油气勘探、环境与工程地质和考古等方面都可不同程度地发挥作用。它是通过分析岩、矿石的磁性差异和磁场特征,探测和研究地质体构造和矿产资源分布形态的一种物理方法。与其他物探方法相比,磁法设备简单、效率高,适用于做面积性区域调查,因而在区域性矿产调查工作中投入的实际工作量较大,也取得了较好的地质效果。
在对实际资料进行处理与解释过程中,通常采用延拓计算、导数计算、场分离等位场转换方法,以及各种反演处理方法,这也是解决各种实际地质问题的重要环节与方法。然而,当地下地质体为斜磁化时,磁异常形态及其与磁体的关系却要复杂得多,此时对实测的磁异常曲线进行处理和定量解释就会产生很大的困难。如果我们根据需要将实测异常换算成重力异常,则可以使推断解释工作变得简单。磁异常是由磁性差异产生的,而重力异常是由密度差异产生的,本质上来说,二者是没有联系的。然而就某些地质体来说,既有较强的磁性,密度也比较大,如一些超基性岩体等,这时所得到的重力异常和磁异常是同源的,此时的磁源重力与实测重力异常往往有很大的可比性。
磁源重力异常的概念是由Baranov[2]于1957年提出来的,通过对磁异常进行垂向积分得到,可以突出区域性和深部的磁异常。这种由磁异常换算出来的重力异常并不是真正实测的重力异常,人们把它称之为“磁源重力异常”,有时又称为“假重力异常”或“伪重力异常”,Baranov给出了一个在特殊情况下的六方位计算方法。使用这个方法时,必须假定地球正常磁场与矿体的磁化强度向量的方向一致,还必须建立一个特殊的坐标系。长谷川博[3]于在这个基础上给出了八方位计算法。谢靖[4]于1978年再次改进这种算法,使计算方法不受以上各条件的限制,计算坐标可以任意选取。
但上述算法都是在空间域内进行推导和计算,推导繁琐、计算量大且计算速度慢,阻碍了其发展。随着傅里叶变换的出现与广泛应用,基于它的运算简便、快捷,推动了许多算法的发展。本次研究便是在频率域内推导出磁源重力的算法,并将其付诸于理论模型和实际资料的应用。
1 磁源重力方法原理
对于同一个磁性体来说,在空间域中建立重力位(引力位)与磁位之间关系的泊松公式[5-7]为
(1)
式中U为磁位;V为重力位;J为磁化强度矢量;G为万有引力常数;σ为磁性体的剩余密度。
设在X、Y、Z轴方向上的单位矢量分别为i、j和k,则
J=Jxi+Jyj+Jzk
(2)
式中Jx、Jy、Jz分别是磁化矢量在X、Y、Z轴三个方向上的投影。
重力位的梯度为
(3)
则式(1)所示的泊松公式可变为
(4)
由式(4)可以算出磁异常在X、Y、Z三个方向上的分量,下面只列出垂直分量
(5)
为方便起见,用P、Q、R分别表示磁性体磁化强度方向的方向余弦,有
P=cosI·cosD,Q=cosI·sinD,R=sinI
(6)
式中I为磁化倾角;D为磁化偏角。
同时磁化强度矢量J在X、Y、Z三个方向上的投影可由式(7)算出
Jx=J·P,Jy=J·Q,Jz=J·R
(7)
对式(5)两端分别做二维傅立叶变换,并应用式(7)可得

(8)
式中u、v分别代表x、y的波数;i是虚数单位(即i2=-1)。
由于有
(9)
这样就可以通过磁异常的垂直分量得到(磁源)重力异常在频率域内的计算公式
Δg(u,v)=Vz(u,v)=
(10)
然而我们实际测得的磁异常通常是地磁场总量Ta,假设地磁场倾角为I0,地磁场偏角为D0,令
P0=cosI0·cosD0,Q0=cosI0·sinD0,R0=sinI0
(11)
于是在频率域内Ta与Za之间的转换公式如式(12)。
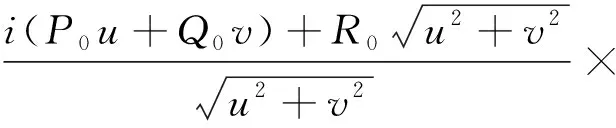
Za(u,v)
(12)
因而,如果用磁异常总量Ta计算磁源重力,只需将式(12)代入式(10)便可得到。
(13)
在实际处理中,常常假设磁性体是由地磁场磁化的,就是说磁性体的磁化方向与地磁场方向一致。这时有P=P0、Q=Q0、R=R0。于是式(13)可以改写为式(14)。
(14)
最后再对式(14)进行傅立叶逆变换就可得到空间域的磁源重力异常。
2 理论模型数据计算
理论模型由处于三个不同深度层的、尺度大小各异的斜磁化直立棱柱体组成,平面位置如图1(a)所示,各棱柱体的具体几何参数见表1所示。各棱柱体的磁化强度均为1 A/m,总磁化强度倾角为45°,偏角为10°,并设定各棱柱体的剩余密度均为0.5 g/cm3。假设地磁场倾角和偏角也分别为45°和10°。正演计算时设定该模型的观测面高度为0 m,测网为101×101,纵横向网格间距为10 m。图1(b)显示了正演的理论磁异常ΔT异常图。从图1(b)可以看出,由于异常叠加,模型的磁异常均受到较大干扰而产生一定的形态变化,很难直接分辨出单个模型的位置和形态。同时也可以看出,要想通过磁异常图(尤其是斜磁化的异常)解释异常体位置大小以及进行处理,都是很困难的事。这还是比较简单的理论模型,而实际地质情况和采集的资料数据会更加复杂。此时我们可以采用磁源重力将复杂的磁异常转换为较为简单的重力异常,再进行处理解释。
于是通过对图1(b)所示的模型磁异常图做磁源重力计算,得到重力异常如图2(a)所示,其数值大小范围为-0.871 mGal~25.701 mGal。通过图2(a)的重力异常与图1(b)的磁异常相比,可以很明显地看出,重力异常比磁异常更简单,更容易识别模型的形态与平面位置。为了验证磁源重力算法的准确性,可以将磁源重力异常与模型理论的重力异常相比较,如图2(b)所示,其数值大小范围为0.712 mGal~25.503 mGal。为了更好从数值上对计算值与理论值进行对比,分别从图2(a)、(b)的等值线图中提取出X=350 m和X=750 m处剖面上的数据,并绘制图3(a)、(b)所示的剖面图,从图中值的对比可以看出,计算值的精确度很高。从图2和图3可以看出,无论是等值线形态还是数据数值大小,都可以确定磁源重力计算的准确性好及精确度高。
3 磁源重力在琼东南盆地的应用
琼东南盆地位于南海北部被动大陆边缘西北侧,位于海南岛东南、西沙群岛以北的海域中,其西以哀劳山-红河断裂与莺歌海盆地分界,东以神狐隆起与珠三凹陷相接,北临海南岛,南界永乐隆起;是一个发育在前新生代基底上的新生代陆缘拉张型含油气盆地,也是长期以来国内、外学者所关注和研究的地域[8-12]。图4是南海琼东南盆地航测并经过初步处理后的磁异常等值线图(白化后),测区范围为:16.80°~19.00°N、108.80°~111.85°E;平面数据网格(网格化后、白化前)为200×200,其中白化部分为海南岛区域。对磁异常数据进行磁源重力计算,其中磁化偏角取0°、磁化倾角取33°左右。图5显示了实测磁异常经过磁源重力计算后得到的重力异常等值线。从处理的结果来看,重力异常数据比磁异常数据要简单得多,且重力异常能够反映出更为细致的构造带和异常分布。
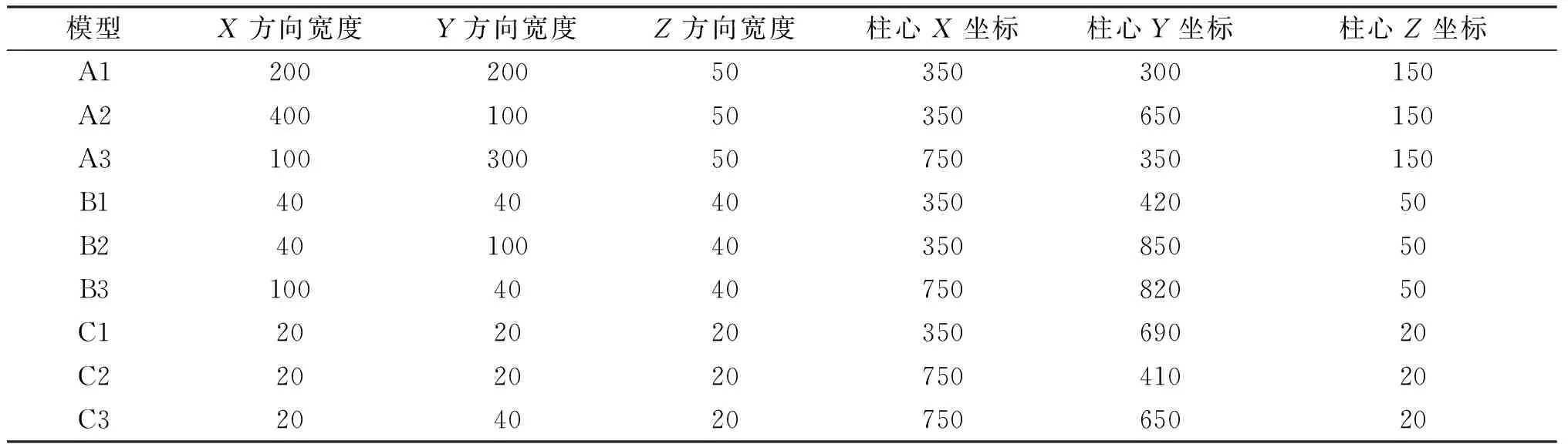
表1 理论模型的各棱柱体几何参数(m)

图1 理论模型各棱柱体的水平面投影分布图和磁异常等值线图Fig.1 Projection of each prism of the theoretical model on the XOY surface and contour map of the magnetic anomalies (a)水平面投影分布图;(b)磁异常等值线图

图2 模型的磁源重力异常图和理论重力异常图的对比Fig.2 Comparison of the pseudo-gravity anomalies and theoretical gravity anomalies (a)重力异常图;(b)理论重力异常图

图3 磁源重力异常和理论重力异常分别在X=350 m(a)和X=750 m(b)处剖面的对比Fig.3 Comparison of pseudo-gravity anomalies and theoretical gravity anomalies along the profile at X=350m and X=750m(a)X=350 m; (b)X=750 m
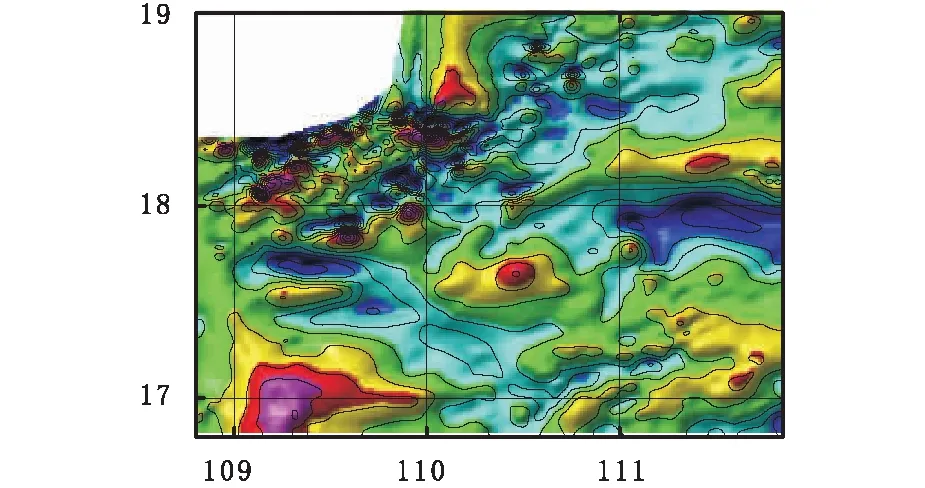
图4 琼东南盆地航测磁异常等值线图Fig.4 Contour map of magnetic anomalies by aerial survey in Qiongdongnan basin
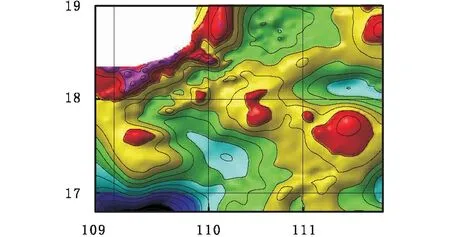
图5 琼东南盆地的磁源重力异常等值线图Fig.5 Contour map of pseudo-gravity anomalies in Qiongdongnan basin
根据以上计算结果中的磁源重力异常可以将琼东南盆地划分为北部隆起区、中央坳陷区和南部隆起区三个大的构造单元。再进一步利用磁源重力异常可以划分更细的构造单元,最终得到区域地质构造单元划分图,如图6所示。这里由磁源重力划分的构造单元反映的是地下磁性体的位置和构造,与其他学者运用重力或地震资料研究绘制的构造单元图[8-11],有一定的不同,但可以看出一些较大的构造单元与其他学者的结果吻合的很好,如崖城凸起、崖北凹陷、陵水低凸起、松涛凸起、神狐隆起及宝岛凹陷等;也有一部分差异较大,如松东凹陷、松南凸起、北礁低凸起、陵水凹陷等。
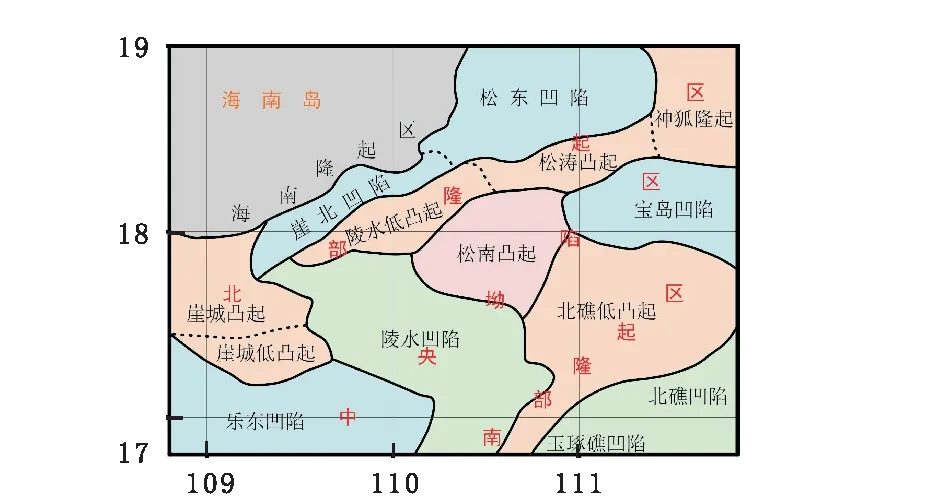
图6 琼东南盆地区域地质构造单元的划分Fig.6 Division of geological tectonic units in Qiongdongnan basin
4 结论
本次研究工作通过磁源重力在理论模型和实际资料中的应用,得到了以下几点结论和认识:
1)磁源重力有简化异常的作用。重力异常比磁异常更加简单、更易处理、更好解释,因此,进行磁源重力计算对资料解释起到了省时省力的作用。
2)这种磁源重力算法不受各种条件的限制,只需要了解和测量当地的地磁场方向,计算出有效磁化倾角即可。计算出的结果并不是真实的重力异常,但横向上可以作为参考进行比较分析。
3)本次研究的磁源重力算法计算速度快、精度高。无论是从理论模型,还是从琼东南盆地的实际资料看,计算的结果都有很高的准确性、精确度和可信度。
参考文献:
[1] 李才明,李军.重磁勘探原理与方法[M]. 北京: 科学出版社,2013.
[2] BARANOV V.A new method for interpretation of aeromagnetic maps:pseudo-gravimetric anomalies [J]. Geophysics,1957,22(2):359-382.
[3] 长谷川博.拟似重力异常的新计算法[J].物理探矿, 1967,20(5):121-125.
[4] 谢靖. 磁源重力异常及其导数的计算方法[J].长春地质学院学报,1978,8(3):62-78.
[5] 曾华霖.重磁资料数据处理程序分析[M].北京:地质出版社,1985.
[6] 穆石敏,申宁华,孙运生.区域地球物理数据处理方法及其应用[M].吉林科学技术出版社, 1990.
[7] 林长松,管志宁,吴朝钧.东海磁源重力异常、重力异常的对比和深部地质构造研究[J].海洋学报,1992,14(5):75-85.
[8] 刘兵,吴世敏,龙根元,等.重力水平梯度矢量法在琼东南盆地基底断裂划分上的应用[J].热带海洋学报, 2011,30(5):74-80.
[9] 雷超.琼东南盆地深水区盆地结构构造及其形成机制研究[D].湖北:中国地质大学(武汉),2009.
[10] 刘兵,吴世敏,龙根元,等.琼东南盆地基底特征及其构造演化[J].地球物理学进展,2012,27(4):1465-1475.
[11] 刘见宝, 孙珍.琼东南盆地新生代构造研究现状及展望[J].海洋地质前沿,2012,28(4):1-9.
[12] 任建业, 雷超.莺歌海—琼东南盆地构造-地层格架及南海动力变形分区[J].地球物理学报,2011,54(12):3303-3314.
