基于积分方程法的任意形状源多次激发三维电磁场反演

李建平，尚通晓, 关艺晓

(1.山东科技大学 山东省沉积成矿作用与沉积矿产重点实验室，青岛 266590；2. 国土资源部地裂缝地质灾害重点实验室，南京 210018 3. 江苏省地质调查研究院，南京 210018)

0 引言

积分方程法是计算三维异常体电磁场的一种有效方法[1-2]，与有限元、有限差分等方法需要全空间进行剖分不同[3～5]，该方法只在异常区域进行剖分，计算量相对较小，尤其适合计算三维电磁场正反演。

在野外勘探中，常用的激发源有接地的电偶源和不接地的回线源，它们均为规则形状，但受实际条件的限制，很多条件下激发源不能布设成规则形状，此外受激发源强度和接收装置的影响，每次观测采集的数据个数都是一定的，但各次观测中的激发点坐标，接收点坐标等参数却不一样，所以不能把不同参数的观测数据直接用于反演。本次研究针对此问题，首先利用文献[6]给出的方法，求出任意形状源产生的一次场，再将激发点和接收点不同的多组电磁场数据统一考虑，实现了此种条件下三维电磁场的反演。

1 任意形状源一次场的计算

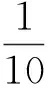
2 积分方程基本理论

根据麦克斯韦方程组、积分方程理论及电场和磁场的张量格林函数，可得均匀大地中三维异常体的积分方程为

(1)

为方便计算，将三维异常体剖分成N个小立方单元，并假设电阻率在每个剖分单元内是均匀分布的，且每个小单元内的电磁场值近似等于其中心点的值，则各剖分单元内电场可用式(2)表示。

(2)

解方程(2)求得异常体内各剖分单元总电场E(rm)后，再利用式(1)的剖分形式

(3)

可求得到空间内任意一点的电场或磁场值。

3 反演方法概述

目前三维电磁场常用的反演方法有共轭梯度法[7-11]、最小二乘法[12-15]、α中心方法[16]、神经网络法[17]等，本研究采用文献[15]给出的方法，把灵敏度矩阵分为线性项和非线性的偏微分项，减少了计算量，提高了精度，再通过经典的阻尼最小二乘法 ，用正演模拟数据拟合实测数据，并逐步修改地电模型参数值 ，最终达到最优拟合，反演得到地下三维异常体电阻率的分布。

反演过程可简单描述如下：

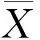
(4)

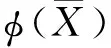
(5)

上式中实测场和理论场值都有x,y,z三个分量，且下标i=1、2、…、m表示每个观测位置点或工作频率点。

(6)

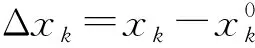
(7)

此时拟合误差被表示成为电导率模型修改量Δx1,Δx2,…,Δxn的多元函数，其取极小值的条件为：

(8)

进一步推导得

(9)

这样分别取j=1、2、…、n，可以推导出如下求解模型修改量的线性方程组:

(PTP+λ)·ΔX=S

(10)

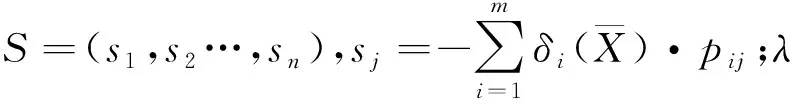
4 源多次激发条件下雅克比矩阵和右端矢量的求取

假设共进行了N次测量，每次测量中测点个数均为m个，但场源和测点的位置各不相同。先按照前文所述方法求出各次测量时的雅克比矩阵P1、P2、…、PN，它们均为m行N列的矩阵。

N次测量后的总雅克比矩阵可用各次测量的雅克比矩阵表示为:

(11)

式(11)为N·m行n列矩阵。

多次测量后的右端总矢量为T=(t1,t2…,tn)，其中元素为：

(12)

将Q、T代入式(10)中并替换PTP和S，即：

(QTQ+λ)·ΔX=T

(13)

利用式(13)代替式(10)求取模型参数的修改量ΔX，从而将多次测量数据应用到一次反演中。式(13)的雅克比矩阵元素为：

(14)

将式(4)代入式(14)得：

(15)

又由式(3)得：

(16)

(17)

求解式(17)需要首先求得异常体各单元中心点处电场对各单元电导率的偏导数，然后再叠加求出地表总场对各单元电导率的偏导数。前文中的Fi、pin具有x、y、z三个分量，展开得：

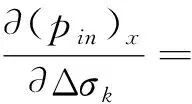
(18)

(19)

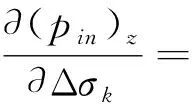
(20)

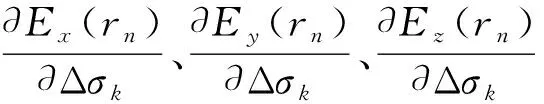
仿照式(2)的求取方法，异常体各单元中心点处电场对各单元电导率偏导数的矩阵方程可表示为：

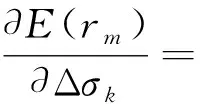
(21)

5 三维电阻率异常体反演算例

针对任意形状源激发的三维异常体反演，设计了以下两个模型算例，第一个算例相对简单，电阻率在异常体内是不变的，剖分的小块数目较少；第二个算例相对复杂，异常体内部的电阻率是变化的，剖分的小块数目较多，而且两个算例激发源的形状不同，从而说明算法的有效性和通用性。

5.1 模型1

模型1如图1所示，均匀大地中存在一个电阻率异常体，其中心点坐标为(0，0，100)，大小为200 m×200 m×50 m ；激发源为一梯形大回线(图2)，中心坐标为(0，0，0)，回线内部有两条测线，共25个测点；激发源工作频率选择为0.01 Hz、0.1 Hz、1 Hz、10 Hz；围岩电阻率为ρ0=100 Ω·m，异常体电阻率真值为ρ=10 Ω·m，将异常体剖分为4×4×1个小块，设各小块内部电阻率分布均匀且等于其中心点电阻率值。

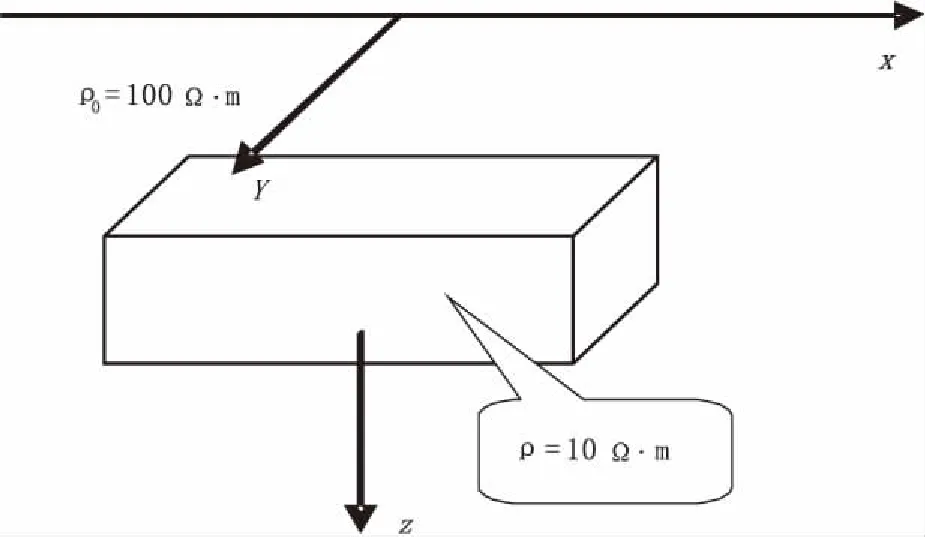
图1 模型1三维示意图Fig．1 The 3D sketch map of model 1

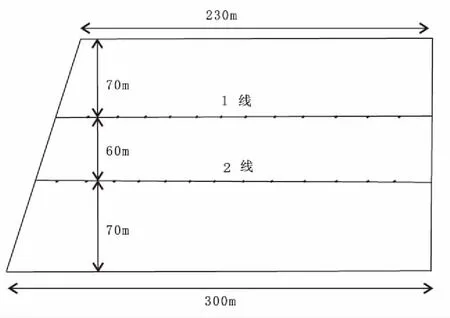
图2 梯形大回线示意图Fig．2 The sketch map of the trapezium loop

先利用一次激发下25个观测点的数据进行反演，反演模型的初始电阻率值为ρ=50 Ω·m，阻尼因子为“1”，阻尼因子缩放系数为10。利用本文算法反演计算各小块的电阻率，经过13次迭代后，反演结果如图3所示，此时拟合差为4.32×10-6，大于给定的阀值1×10-7，且拟合差不再随迭代次数的增加而减小，各小块电阻率反演值与真值相差较大，反演失败。

经分析可知，反演失败的原因在于参加反演的数据量不足。如果用两次观测的数据进行反演，设激发源中心点分别为(0，0，0)和(300，0，0)，每次观测均为25个测点，共50个测点，其余参数与前文相同。经过9次迭代后，反演结果如图4所示，此时拟合差为1.06×10-8，小于给定的阀值1×10-7，反演结束，且各小块电阻率反演值收敛于真值，说明算法是正确的。

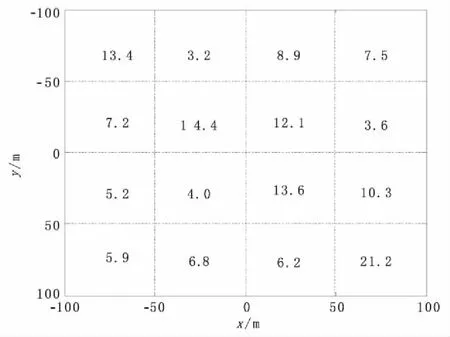
图3 单次观测异常体电阻率参数反演结果Fig．3 Resistivity inversion results of abnormal body in single measurement

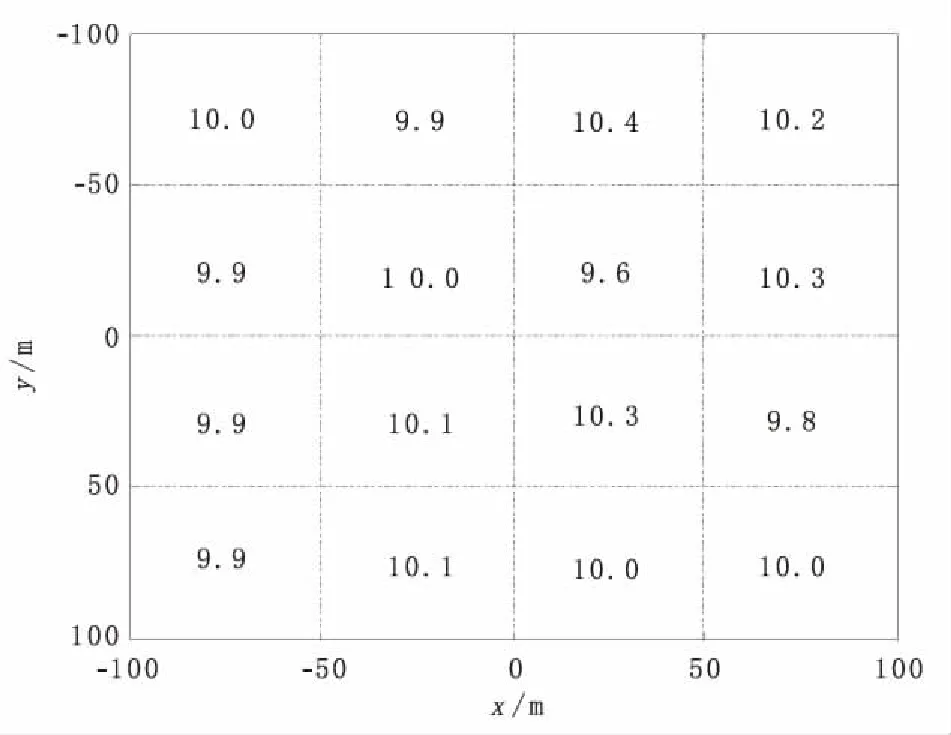
图4 两次观测异常体电阻率参数反演结果Fig．4 Resistivity inversion results of abnormal body in two measurements

5.2 模型2

模型2如图5所示，均匀大地中存在一个电阻率异常体，其中心点坐标为(0，0，200)，大小为300 m×300 m×150 m；激发源为一等边三角形大回线，边长1 000 m(图6)，回线内部有5条测线，42个测点，利用三次观测的数据进行反演，中心点分别为(-500，0，0)、(0，0，0)和(500，0，0)；激发源工作频率选择为0.01 Hz、0.1 Hz、1 Hz、10 Hz、100 Hz；围岩电阻率为ρ0=100 Ω·m，异常体电阻率见下图模型真值，将异常体剖分为 个小块，设各小块内部电阻率分布均匀且等于其中心点电阻率值。反演中模型的初始电阻率值为ρ=300 Ω·m，阻尼因子为“1”，阻尼因子缩放系数为10，经过11次迭代后，此时拟合差为9.21×10-8，小于给定的阀值1×10-7，反演结束，反演结果如图7～图9所示。

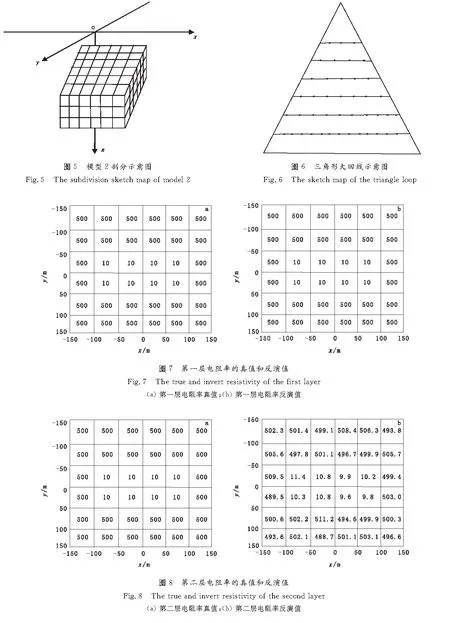
图9 第三层电阻率的真值和反演值Fig．9 The true and invert resistivity of the third layer(a) 第三层电阻率真值;(b) 第三层电阻率反演值

图7、图8、图9为模型2各层的反演结果。模型2在z方向上剖分为三层 ，图7(b)为第一层剖分小块在150 m处xoy面上的反演结果，图8(b)为第二层剖分小块在200 m处xoy面上的反演结果，图9(b)为第三层剖分小块在250m处xoy面上的反演结果。从图中可看出，尽管电阻率在模型体内是变化的，而且模型体剖分后的小块数目也比较多，但把三次观测的数据同时用于计算，反演的结果仍收敛于真值，说明本文算法不仅适用于异常体电阻率不变的简单情况，也适用于异常体电阻率变化的复杂情况。

6 结论

本次研究提出并实现了均匀大地中任意形状源多个位置激发下的三维电阻率反演算法，通过模型试算得出如下结论：

1)积分方程只针对异常体单元反演，反演算法的效率较高，计算量相对较小，为三维电阻率反演应用奠定了坚实的基础。

2)反演中激发源可以为任意形状，更加符合野外实际情况。

3)将激发点和接收点不同的多次观测的电磁场数据用于一次反演中，有效解决了反演数据不足导致的参数不收敛问题。

参考文献：

[1] HOHMANN G W.Three dimensional induced polarization and electromagnetic modeling [J].Geophysics 1975, 40(2):309-324.

[2] WANNAMAKER P E, HOHMANN G W， SANFILIPO W A. Electromagnetic modeling of three dimensional bodies in layered earths using integral equations[J].Geophysics 1984,49(1):60-74.

[3] 朱伯芳.有限单元法原理与应用[M].北京:水利出版社,1979.

[4] 徐世浙.地球物理中的有限单元法[M]. 北京:科学出版社,1994.

[5] 周熙襄. 电法勘探数值模拟技术[M]. 成都:四川科学技术出版社,1986.

[6] 李建平,李桐林,张亚东. 层状介质任意形状回线源瞬变电磁场正反演研究[J].物探与化探，2012,36(2):256-259.

[7] 林昌洪，谭捍东，舒晴，等.可控源音频大地电磁三维共轭梯度反演研究[J].地球物理学报，2012，55(11)：3829-3839.

[8] MACKIE R L,MADDEN T R.Three-dimensional magnetotelluric inversion using conjugate gradients[J]. Geophys,J.Int,1993,115:215-229.

[9] NEWMAN G A,ALUMBAUGH D L.Three-dimensional magnetotelluric inversion using non-linear conjugate gradients[J]. Geophys,J.Int,2000,140:410-424.

[10] 胡祖志，胡祥云，何展翔.大地电磁非线性共轭梯度拟三维反演[J].地球物理学报，2006，49(4)：1226-1234.

[11] LIN C H,TAN H D,TONG T.Three-dimension conjugate gradient inversion of magnetotelluric full information data[J]. Applied Geophysics,2011,8(1):1-10.

[12] 刘斌，李术才，李树忱，等.基于不等式约束的最小二乘法三维电阻率反演及其算法优化[J].地球物理学报，2012，55(1)：260-268.

[13] 宛新林，席道瑛，高尔根，等.用改进的光滑约束最小二乘正交分解法实现电阻率三维反演[J].地球物理学报，2005，48(2):439-444.

[14] SASAKI Y.3-D resistivity inversion using the finite-element method [J].Geophysics,1994,59(11):1839-1848.

[15] EATON P A. 3D electromagnetic inversion using integral equation[J]. Geophysical prospecting, 1989, 37:407-426.

[16] PETRICK W R JR, SILL W R, WARD S H. Three-dimensional resistivity inversion using alpha centers[J]. Geophysics,1981,46(8):1148-1163.

[17] EL-QADY G,USHIJIMA K. Inversion of DC resistivity data using neural networks[J].Geophysical Prospecting,2001,49(4):417-430.