巧用开普勒第三定律解决天体运动问题
2014-06-27吴正飞
吴正飞
(如东高级中学 江苏 南通 226400)
自古以来,人们一直对天体的运动进行着长期的探索和研究,从亚里士多德和托勒密主张的地心说到哥白尼提出日心说再到第谷对行星的运动进行了长期的观测和记录,最终德国杰出的天文学家开普勒在第谷精确数据的基础上进行了创造性的研究和思考并建立了行星运动的三大定律.其中包括开普勒第一定律(轨道定律)、开普勒第二定律(面积定律)、开普勒第三定律(周期定律).
下面重点研究开普勒第三定律在天体运动问题中的巧妙应用.
开普勒第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.即
式中a为半长轴,T为公转周期.
1 开普勒第三定律解决同“中”行(卫)星问题
开普勒第三定律虽然是根据行星绕太阳的运动总结出来的,但对于卫星绕行星的运动也同样适用.在天体运动中经常遇到绕同一个中心天体运动的行星或卫星问题,此时可利用开普勒第三定律建立行星或卫星之间的半径和周期之间的联系.
【例1】哈雷彗星最近出现的时间是1986年.天文学家哈雷预言,这颗彗星将每隔一定时间就会出现,请预算下一次飞近地球是哪一年?提供数据:
(1)地球公转接近圆,彗星的运动轨道则是一个非常扁的椭圆,如图1所示;
(2)彗星轨道的半长轴R1约等于地球轨道半长轴R2的18倍.

图1
解析:设彗星绕太阳运动的周期为T1,地球的公转周期为T2,根据开普勒第三定律,有
解得
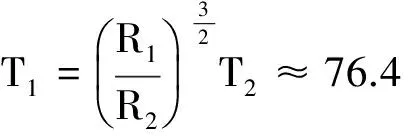
则哈雷彗星下次出现的时间是
1986年 + 76年 = 2062年
解题点拨:在解决同“中”行(卫)星问题时,必须抓住相同的中心天体这个开普勒第三定律适用的关键条件,然后由轨道半径就可以确定周期,或由周期就可以确定半径,从而找到问题的突破口,解决问题.
2 开普勒第三定律解决同步卫星问题
同步卫星问题是高中阶段学习中的常见问题,是人造卫星中的重点也是难点.一般需要掌握同步卫星的位置、周期、高度、线(角)速度等,根据同步卫星和其他卫星均以地球为中心,符合开普勒第三定律的适用条件,因此利用开普勒第三定律和其他卫星的周期或半径就可求得同步卫星对应的周期和高度等.
【例2】月球环绕地球运动的轨道半径约为地球半径的60倍,其运行周期约为27天,现应用开普勒定律计算:在赤道平面内,离地多高时,人造地球卫星可随地球一起转动,就像其停在天空一样(同步卫星).(已知R地= 6.4×103km)
解析:设同步卫星运动的半径为R1,周期为T1(此周期与地球自转周期相同),月球的轨道的半径为R2,周期为T2,根据开普勒第三定律有
解得
则同步卫星离地面的高度为
h=R1-R地=5.67R地=3.63×106m
解题点拨:月球、同步卫星都是地球的卫星,它们的周期已知,应用开普勒第三定律可以确定它们轨道半径之间的关系,从而使问题简化.
3 开普勒第三定律解决变轨问题
卫星在轨期间自主改变运行轨道的过程称为变轨.人造卫星、宇宙飞船(包括空间站)在轨道运行的过程中,常常需要变轨.变轨过程中卫星的轨道为椭圆,地球处于焦点上.在变轨问题中通常需要计算运行时间,因其轨道不是圆,所以不能利用圆周运动的知识求解.
若利用开普勒第三定律求解,问题就会变得非常简单,但要注意公式中的a分别是变轨前圆周运动的半径和变轨中的椭圆轨道的半长轴.
【例3】飞船沿半径为R的圆周绕地球运动,其周期为T,如图2所示.如果飞船要返回地面,可在轨道上的某点A将速度降低到适当的数值,从而使飞船沿着地心为焦点的椭圆轨道运行,椭圆与地球表面在B点相切,求飞船由A点到B点所需的时间.(已知地球半径为R0)

图2
解析:无论飞船是沿圆轨道运行还是沿椭圆轨道运行,飞船都是绕地球运动,所以运行时间与半径之间的关系满足开普勒第三定律,由
解得
则飞船由A点到B点所需的时间为
解题点拨:变轨在卫星运行中很常见,变轨过程中由于卫星始终绕同一天体运动,所以开普勒第三定律仍然适用,只要能明确对应的周期和半径,问题就会迎刃而解.
4 开普勒第三定律解决卫星“追及和相遇”问题
地面上的物体常常出现追及和相遇问题,关键是找出它们的位移、速度和时间等关系,运动路线应该在同直线上.天体运动中也有追及和相遇问题,它与地面上的追及相遇问题在思维有上相似之处,即也是找出一些物理量的关系,但它也有不同之处,有其自身特点.一般根据万有引力提供向心力和圆周运动的知识求解,但过程较繁.若利用开普勒第三定律来建立两者之间的半径和周期的关系,则会令问题简化.但要注意当天体速度增加或减少时,对应的圆周轨道会发生相应的变化,所以天体不可能在同一轨道上追及或相遇,但可到达与中心天体同一连线上,此时通常我们也可认为卫星即相遇.
【例4】某行星和地球绕太阳公转的轨道均可视为圆.每过N年,行星会运行到日地连线的延长线上,如图3所示.求该行星与地球的公转半径的比值.

图3
解析:从行星运动到日地连线的延长线上到下一次再到日地连线延长线上,地球比该行星转过的角度大2π ,设行星的周期为T,由此可知
即
解得
又地球与该行星都绕太阳转,则根据开普勒第三定律得
所以
解题点拨:两卫星绕同一中心天体运动,半径与周期的关系可由开普勒第三定律确定.不同轨道上的卫星不能直接追及和相遇,但可到达与中心天体同一连线上,通过圆心角找到周期关系,进而解决半径问题.
本文重点介绍了开普勒第三定律在同“中”行星、同步卫星、以及卫星变轨、追及这4类问题中的应用.开普勒第三定律是解决天体运动问题的重要途径.在应用过程中,我们只要抓住“一个中心”(同一中心天体),找到“两者关系”(周期和半径关系),问题定会迎刃而解.
