探地雷达有限元数值模拟及衰减特性探讨

陈承申 ，冯德山

(1.铁道第三勘察设计院集团有限公司，天津 300251;2.中南大学 地球科学与信息物理学院，长沙 410083)

0 引言

探地雷达(Ground penetrating radar,GPR)正演模拟一直是该领域理论研究的热点[1-2]，通过对典型地质模型正演计算结果的分析，加深了对GPR反射剖面的认识与理解[3-4]，对GPR资料解释有指导作用。在GPR正演模拟中，时域有限差分法[5-7](FDTD)因简单灵活而被广泛采用，但它不适合复杂的物性分界面；有限单元法[8](Finite Element Method，FEM)不需要计算内部边界条件，适用于物性复杂问题、求解过程规范化，具有广泛的适应性；沈飚[9]进行了GPR简单模型正演；底青云、王妙月[10-11]推导了含衰减项的探地雷达波有限元方程，实现了复杂形体的GPR波的FEM正演模拟和偏移处理；由于探地雷达波在地层中传播能量会迅速衰减[12]，在进行采集参数设置及数据处理时必须考虑到衰减媒质对探地雷达波的影响，Tiao等[13]利用离散时域Galerkin进行色散介质中的GPR正演；刘四新、曾昭发[14]利用时域有限差分法，对探地雷达波在频散介质中传播进行了数值模拟。

作者通过对雷达波在衰减媒质中传播特性的研究，定义了衰减比的概念及其计算公式，使用带衰减项的探地雷达波方程，对非衰减媒质和衰减媒质的中心电磁脉冲源模型模拟计算，这对雷达波在介质中的传播方式有更深刻的认识[15]。

1 GPR波动方程推导

Maxwell方程组描述了电磁场的运动学和动力学规律[16]，基于电磁波理论，高频电磁波在媒质中的传播规律也应服从Maxwell方程组，其方程组的微分形式可以表示为[17-18]：

▽×E=-∂B/∂t

(1)

▽×H=J+∂D/∂t

(2)

▽·D=ρ

(3)

▽·B=0

(4)

式中B为磁感应强度(T)；E为电场强度(V/m)；D为电位移(C/m2)；H为磁场强度(A/m)；ρ为电荷密度(C/m3)；J为电流密度(A/m2)。

本构方程为式(5)：

D=εE,B=μH,J=σE

(5)

式中μ为磁导率(H/m);ε为介电常数(F/m);σ为电导率(S/m)。

把方程式(5)代入方程式(1)，并求旋度得到式(6)

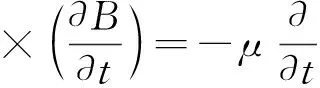
(6)

考虑到式(7)：

▽×▽×A=-▽2A+▽(▽·A)

2.3.1 理论考核。以出科考核方式（选择题与病案分析题）对学生进行综合评价，主要考察以下几个方面：对急性心肌梗死这一严重胸痛疾病的理论知识的掌握，如病理学分析、诊断及鉴别诊断、治疗；实践患者的病史采集、体格检查、疾病诊断及鉴别诊断、治疗方案。结合带教老师对学生平时表现的评定，在成绩中予以一定的比例（20%）。即总成绩=理论成绩（80%）+平时表现成绩（20%）。规定“优秀”≥85分，“良好”≥75分，“及格”≥60分，“不及格”＜60分。

(7)

由于ε、μ、σ为坐标的渐变函数，它们的空间导数是可以忽略的，则在式(7)中右边的第二项▽(▽·A)=0

整理得式(8)。

(8)

假设雷达波激励源如电场源SE或磁场源SH，代入到式(8)中得到式(9)。

(9)

同理对式(2)中第二式两边求旋度，可得式(10)。

(10)

式(9)与式(10)表明，磁场H和电场E及其分量满足相同的微分方程，可以得到时空域GPR波的二维有限元方程：

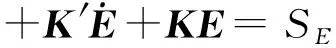
(11)

(12)

2 衰减特性分析

目前商用探地雷达大多使用调幅脉冲激励源，其子波形式为：

f(t)=t2e-α tsinω0t

(13)

式中ω0为GPR天线的主频；α值的大小影响着电磁波在传播过程中能量衰减的速率，这里α=0.93ω0。图1为主频100MHz的GPR子波图。

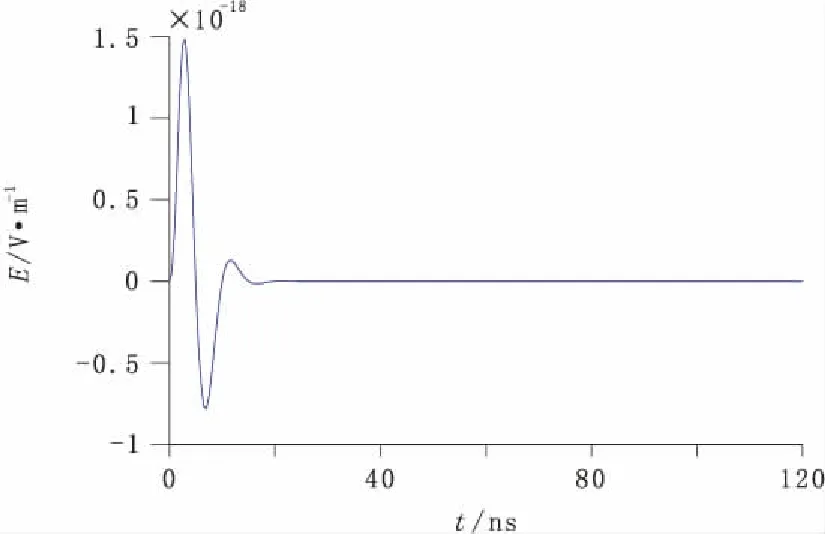
图1 100 MHz电磁脉冲子波Fig．1 100MHz electromagnetic pulse wavelet

为了说明雷达波在不同介质中的传播特性，建立模型如图2所示，9.0 m×9.0 m大小的正方形均匀模型，单元大小为0.1 m×0.1 m，并把中心频率为100 MHz的电磁脉冲激励源置于模拟区域的正中心，采样间隔为0.5 ns。

图2 均匀模型示意图Fig．2 Sketch map of homogeneous model

2.1 非衰减媒质

设置模型介质为干花岗岩，其中相对介电常数为ε=5，电导率为σ=10-7S/m，对于探地雷达电磁波，其频率ω很高，有10-7=σ≪εω=0.027 8，衰减项(σ/ε)(∂E/∂t)或者(σ/ε)(∂H/∂t)的作用几乎可以忽略，此时式(9)与式(10)变为纯波动方程，GPR有限元波动方程变为式(14)与式(15)。

MЁ+KE=SE

(14)

(15)

图3分别给出非衰减媒质带衰减项和不带衰减项模拟计算结果。

2.2 衰减媒质

模型设置为浸水花岗岩介质，其中电导率为σ=0.01 S/m，相对介电常数为ε=7，当媒质为良导体或者近似于良导体时，σ较大，0.01=σ≪εω=0.038 9不成立，衰减项(σ/ε)(∂E/∂t)或者(σ/ε)(∂H/∂t)的作用不能忽略，此时探地雷达波在这种介质中传播时，就会被媒质吸收和发生频散(图4)。

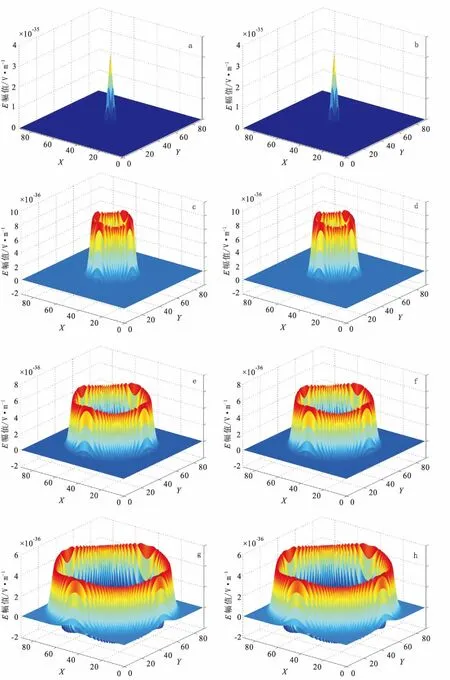
图3 GPR波在干花岗岩中传播时的全波场快照Fig．3 The full field snapshot of the GPR wave transmitted in the dry granite(a)带衰减项5 ns时刻全波场快照；(b)不带衰减项5 ns时刻全波场快照；(c)带衰减项15 ns时刻全波场快照；(d)不带衰减项15 ns时刻全波场快照；(e)带衰减项25 ns时刻全波场快照；(f) 不带衰减项25 ns时刻全波场快照；(g)带衰减项35 ns时刻全波场快照；(h) 不带衰减项35 ns时刻全波场快照

3 干花岗岩模型与浸水花岗岩模型正演结果对比

为了验证在GPR正演模拟计算时，当σ≪εω时，衰减项(σ/ε)(∂E/∂t)和(σ/ε)(∂H/∂t)的作用几乎可以忽略，当地下介质导电性较强甚至很强的时候，电导率σ值大，σ≪εω不成立，衰减项(σ/ε)(∂E/∂t)和(σ/ε)(∂H/∂t)的作用不可以忽略，作者自定义了探地雷达电磁波衰减比的概念及其计算公式。

概念 1 GPR电磁波在介质中传播时，可以计算得到t时刻带衰减项的磁场 (或电场)峰值，设该峰值为a,不带衰减项的磁场(或电场)峰值，设该峰值为b，b与a这两个峰值的差值与不带衰减项的磁场(或电场)峰值b的比值，这个比值称为GPR电磁波衰减比[15]。

GPR电磁波衰减比可由式(16)计算得到[15]

(16)

利用GPR二维有限元正演模拟程序,对非衰减介质(σ≪εω成立，干花岗岩相关参数模型)和衰减介质(σ≪εω不成立，浸水的花岗岩相关参数模型)分别进行数值模拟，并得出模拟结果(如表1所示)，截取电磁脉冲发射后的某些时刻的电场峰值，将这些值代入计算公式(16)，可以得到不同时刻不同介质的衰减比。

通过讨论分析，从表1中数据可以看出,干花岗岩模型GPR电磁波在45 ns时,衰减比仅为0.005%，而在浸水花岗岩模型中，GPR电磁波在15ns时，其GPR电磁波衰减比就已经为58.158%，到45 ns时更是高达94.877%，这说明了衰减项在非衰减媒质GPR正演模拟时，是可以不用考虑其吸收作用，相反在衰减媒质GPR正演模拟时，却是必须研究的一项重要内容。

4 结论

通过对两种性质相反的介质模型的探地雷达正演模拟计算，说明了探地雷达电磁波在衰减介质中传播时能量会被介质迅速吸收，衰减项的作用明显；在非衰减介质中传播时能量被吸收的很少，衰减项是可以忽略不计的。作者通过给出的GPR电磁波衰减比概念，为理解雷达波在不同介质中传播的特性，提供了一种新的思路及方法。因此在探地雷达正演模拟计算时，必须考虑衰减项的衰减吸收作用，这样的计算结果才更贴近实际情况。

表1 干花岗岩与浸水花岗岩模型正演结果对比表

参考文献：

[1] FENG D S, DAI Q W. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD[J]. NDT&E International, 2011,44(6): 495-504.

[2] SHAARI A, AHMAD R S, CHEW T H. Effects of antenna-target polarization and target-medium dielectric contrast on GPR signal from non-metal pipes using FDTD simulation[J]. NDT & E International, 2010, 43(5): 403-408.

[3] JAMES IRVING, ROSEMARY KNIGHT. Numerical modeling of ground-penetrating radar in 2-D using MATLAB[J] .Computers & Geosciences, 2006,32 (9): 1247-1258．

[4] GIANNOPOULOS A. Modelling ground penetrating radar by GprMax[J]. Construction and Building Materials , 2005, 19(10): 755-762．

[5] 刘四新，曾昭发，徐波. 三维频散介质中地质雷达信号的FDTD数值模拟[J]. 吉林大学学报:地球科学版, 2006, 36(1)：123-127．

[6] BERGMANN T，ROBERTSSON J O.A，HOLLIGER K. Numerical properties of staggered finite-difference solutions of Maxwell’s equations for ground-penetrating radar modeling[J]. Geophysical Research Letters, 1996, 23(1):45-48．

[7] CARCIONE，JOSE M. Radiation patterns for 2-D GPR forward modeling[J]. Geophysics, 1998, 63(2):424-430．

[8] 王妙月，郭亚曦，底青云. 二维线性流变体波的有限元模拟[J]. 地球物理学报, 1995, 36(4):499-506．

[9] 沈飚. 探地雷达波波动方程研究及其正演模拟[J]. 物探化探计算技术，1994，16(1)：29-33．

[10] 底青云，王妙月. 雷达波有限元仿真模拟[J]. 地球物理学报，1999,42(6):818-825．

[11] DI QING-YUN，WANG MIAO-YUE. Migration of ground-penetrating radar data with a finite-element method that considers attenuation and dispersion[J]. Geophysics, 2004, 69(2):472-477．

[12] RICHARD D, MILLER.Vertical resolution of a seismic survey in stratigraphic sequences less than loom deep in Sortheastern Kansas[J]. Geophysics,1995,60(2):423-430．

[13] LU TIAO, CAI WEI, ZHANG PING-WEN. Discontinuous Galerkin Time-Domain Method for GPR Simulation in Dispersive Media[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(1):72-80．

[14] 刘四新,曾昭发.频散介质中地质雷达波传播的数值模拟[J].地球物理学报,2007,50(1): 320-326.

[15] 陈承申. 探地雷达二维有限元正演模拟[D].长沙:中南大学，2011.

[16] YEE K S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media[J].IEEE Transactions on Antennas and Propagation,1996,14 (3):302-307.

[17] TAFLOVE A. Re-inventing electromagnetics:supercomputing solution of Maxwell’s equations via direct time integration on space grids[J]. Computing Systems in Engineering, 1992, 3(1):153-168.

[18] ALVAREZ G B, LOULA A F D, DUTRA DO CARMO E G,et al . A discontinuous finite element formulation for the Helmholtz equation. Comput[J]. Methods Appl. Mech. Engrg., 2006,195:4018-4035.