起伏地形下偶极-偶极激电测深二维反演软件开发及应用
2014-06-27顾观文吴文鹂林品荣
顾观文 , 吴文鹂 , 林品荣 , 梁 萌
(中国地质科学院 地球物理地球化学勘查研究所, 廊坊 065000)
0 前言
基于阵列方式的激电测深观测,由于工作效率高、观测数据密度大,在资源勘查、工程和环境勘察等方面应用广泛。其观测数据的处理解释,目前国内主要依赖于国外商用高密度电阻率法数据处理解释软件,国外有代表性的高密度电法二维成像软件为Res2dinv和Earthimage 2D,Res2dinv为美国Geotomo公司开发,目前已授权给瑞典ABEM公司和德国DMT公司,软件可对视电阻率和视激电数据进行二维反演成像,其突出特点是能灵活支持多种观测装置。Earthimage 2D为美国AGI公司与其高密度电法仪配套的视电阻率/视激电数据二维反演成像软件。
作者在前人工作基础上[1-3],采用第二类齐边界条件结合相应网格剖分技术实现偶极-偶极激电测深二维正演计算,并将其引入偶极—偶极激电测深二维反演中,同时在可视化开发环境下将二维反演与可视化技术进行有机集成,形成集数据输入、数据可视、反演计算和结果输出为一体的二维反演软件,通过理论模型合成数据和实测数据的反演表明,研制形成的二维反演软件具备一定的实用性,并能与物化探所研制的大功率多功能电法仪器配套使用。
1 二维正反演算法
1.1 正演模拟
1.1.1 波数域点源电位的变分问题[4-6]
三维点源电场的总电位通过沿走向方向的傅立叶变换至波数域后,可将三维点源直流电场的边值问题转化为2.5维直流电场的边值问题(式(1))来进行处理。
(1)
此时波数域点源二维直流电位U所对应的变分问题为式(2)
(2)
式(1)和式(2)中,Ω为研究区域;Γs和Γ∞为研究区域的地面边界和无穷远边界;σ为介质电导率;κ为傅立叶变换波数;r为电源点至Γ∞积分点的距离;K0、K1为零阶、一阶第二类修正贝塞尔函数;n是Ω的外法向。
1.1.2 齐次边界条件的引入及模型剖分[4,7]

为了适应简化后的边界条件,在模型网格剖分时,将计算区域划分为观测区和扩展区,观测区为地面电极(包括供电和测量电极)布置区,扩展区是在观测区的基础上分别沿测线方向和深度方向扩展形成的区域(图1),以近似无穷远边界。观测区沿测线和深度方向按测点间距等间隔剖分,在已剖分观测区的基础上,沿观测区测线方向左右两边及深度方向扩展网格数通常为13,扩展区网格步长按1.3倍递增[8]。
边界条件简化后,式(2)的变分问题简化为:
(3)
用有限单元法求变分问题(3)[5],归结到求波数域中各节点上电位的线性方程组
κU=s
(4)
解线性方程组(4),求得各节点波数域中的总电位U。
1.1.3 视电阻率和视极化率的计算
通过对波数域中电位U,由式(5)做傅立叶余弦逆变换求得主剖面上的三维空间中的总电位V[5]。
(5)
由各节点的总电位V及对应的装置系数,可得偶极-偶极测量装置的视电阻率表达式[9]为:
ρs(A,B,M,N)=K(A,B,M,N)[V(A,M)-V(A,N)-V(B,M)+V(B,N)]
(6)
式(6)中:K(A,B,M,N)为偶极装置的装置系数;V(A,M)、V(A,N)、V(B,M)和V(B,N)分别为A点供电M、N处电位和B点供电M、N处电位,供电电流为常数,一般假设为1 A。计算出各节点的电位后,即可实现偶极-偶极装置视电阻率的计算,采用等效电阻率法求取视极化率[9]。
1.2 视电阻率和视极化率数据的反演 [1]
采用带先验信息的最小二乘反演方法,目标函数为
φ=‖Wd(Δd-AΔm)‖2+‖Wm(m-mb+Δm)‖2
(7)
式(7)中 :m为预测模型参数矢量;mb为基本模型参数矢量;Δd为实测视电阻率与正演视电阻率的数据差矢量;A为偏导数矩阵;m、mb、Δd和A为取对数后的值。Wd=diag(1/σ1,1/σ2,…,1/σN)为数据的拟方差矩阵;σi为第i个数据的均方误差;Wm是模型加权矩阵,即模型先验信息。式(7)对Δm求导并令其等于零,可得到线性方程组(8)
(8)

图1 正演计算区域网格剖分Fig.1 Subdividing of region for forward modeling
解方程组(8)得到的模型修改量Δm,将Δm与m相加,得新的预测模型参数矢量,继续下一次迭代,直至平均均方误差满足要求。平均均方误差rms定义为
(9)
按照Seigel(1959)理论,如果地下空间由M块不同电阻率ρj和本征极化率ηj的岩矿组成(j=1,2,…,M),视极化率响应可表示为
或写为矩阵形式
ηa=Aη
(10)
式中ηa是视极化率响应矢量;η为本征极化率参数矢量;A是偏导数矩阵。最小二乘反演方法的目标函数为
φ=‖Wd(ηa-Aη)‖2+‖Wη(η-ηb)‖2
(11)
极化率模型增量求解与电阻率模型增量的求解过程相同,偏导数阵A已在视电阻率反演过程中求得,因此视极化率的反演计算量减小。
2 软件实现及模型检验
软件运行环境:Windows XP/Win7。软件开发工具:MS VC6.0,Compaq Fortran6.6。
2.1 软件的功能组成及集成实现
二维反演软件系统主要包括数据输入、数据显示、反演计算和反演结果的输出等功能(图2)。
软件集成环境基于VC6.0,数据输入、数据显示和结果输出模块采用VC6.0编写,可在源代码级别上基于类对象方式由集成程序编译使用。二维反演计算模块由FORTRAN语言编写,使用Compaq Fortran编译形成动态库,提供接口由程序主进程调用。
集成后形成的软件界面如图3所示。界面中左边部分显示信息包括电极个数、点距、数据点数、最大最小隔离系数和反演迭代误差等信息,右边部分上部为实测数据拟断面,中部为最后一次迭代反演的正演数据拟断面,下部为反演模型断面,通过界面上迭代误差大小、实测和正演拟断面的相似程度可衡量反演结果的有效程度。

图2 软件功能组成Fig.2 Composition of software function

图3 二维反演软件界面Fig.3 Interface of 2D inversion software
2.2 模型检验
对施加5% 随机噪声的两个地电模型(模型来源于“2005年全国电法及电磁法勘探正反演软件推优会”)的合成数据进行二维反演试算,以检验二维反演程序的有效性。
2.2.1 模型一
装置参数:80根电极,点距为5 m,最小隔离系数为“1”,最大隔离系数为20。
模型描述:在均匀围岩中存在一个低阻高极化异常体。围岩电阻率为100 Ω·m,极化率为“1”。异常体电阻率为10 Ω·m,极化率为10。异常体的宽度和向下延伸长度分别为20 m和10 m,上顶距地表深度为10 m。异常体从测线坐标190 m开始,延续到坐标210 m。模型示意图见图4。
反演结果:图5和图6为迭代5次的反演结果,RMS(均方误差)为6%,从反演断面图可以看出低阻高极化异常体得到了很好地反映,反演模型断面和真实理论模型一致。
2.2.2 模型二
装置参数:60根电极,点距为5 m,最小隔离系数为“1”,最大隔离系数为20。
模型描述:在均匀围岩中分别存在一个低阻高极化体和一个高阻高极化体。围岩电阻率为10 Ω·m,极化率为10。异常体1电阻率为2 Ω·m,极化率为50,异常体2电阻率为 50 Ω·m,极化率为50。异常体1和异常体2的宽度和向下延伸长度均为15 m和10 m,上顶距地表的深度为10 m。横向上第一个异常体从100 m开始延续到115 m,第二个异常体从210m开始延续到225 m。模型示意图见图7。
反演结果:图8和图9为迭代5次的反演结果,RMS(均方误差)为7%,从图中可以看出,两个异常体在横向和纵向上都得到了很好的归位,反演断面和真实模型断面(图7)一致。
3 应用实例
作者采用本文编制的偶极—偶极激电测深二维反演软件,对内蒙某工区的500线相位激电资料进行二维反演。
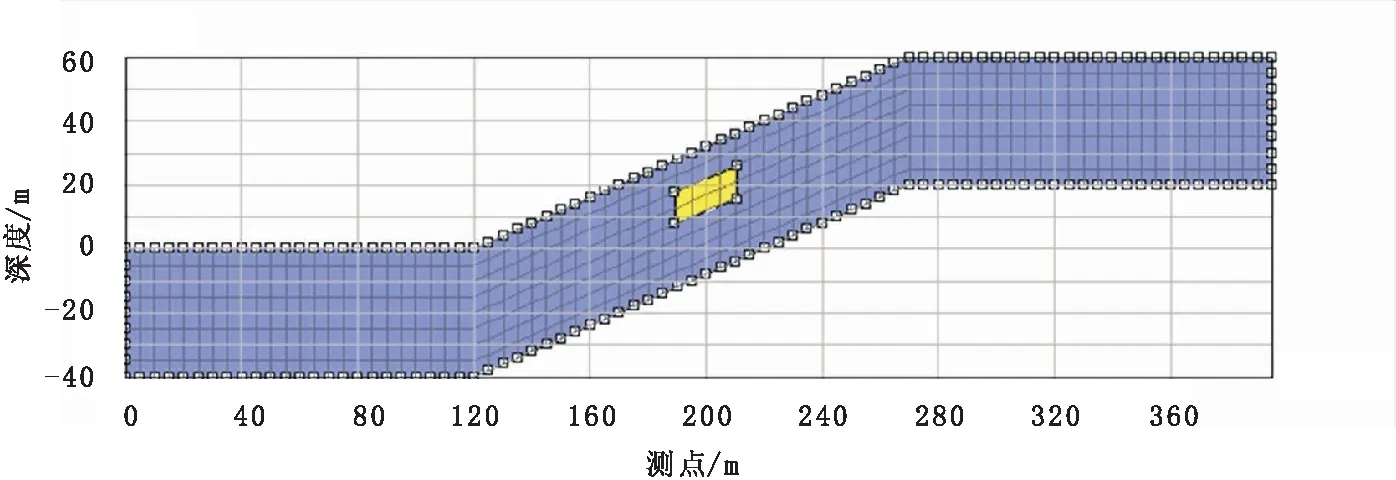
图4 模型一示意图Fig.4 Sketch of model 1

图5 反演电阻率断面图Fig.5 Resistivity section of inversion model

图6 反演极化率断面图Fig.6 IP section of inversion model

图7 模型二示意图Fig.7 Sketch of model 2

图8 反演电阻率断面图Fig.8 Resistivity section of inversion model
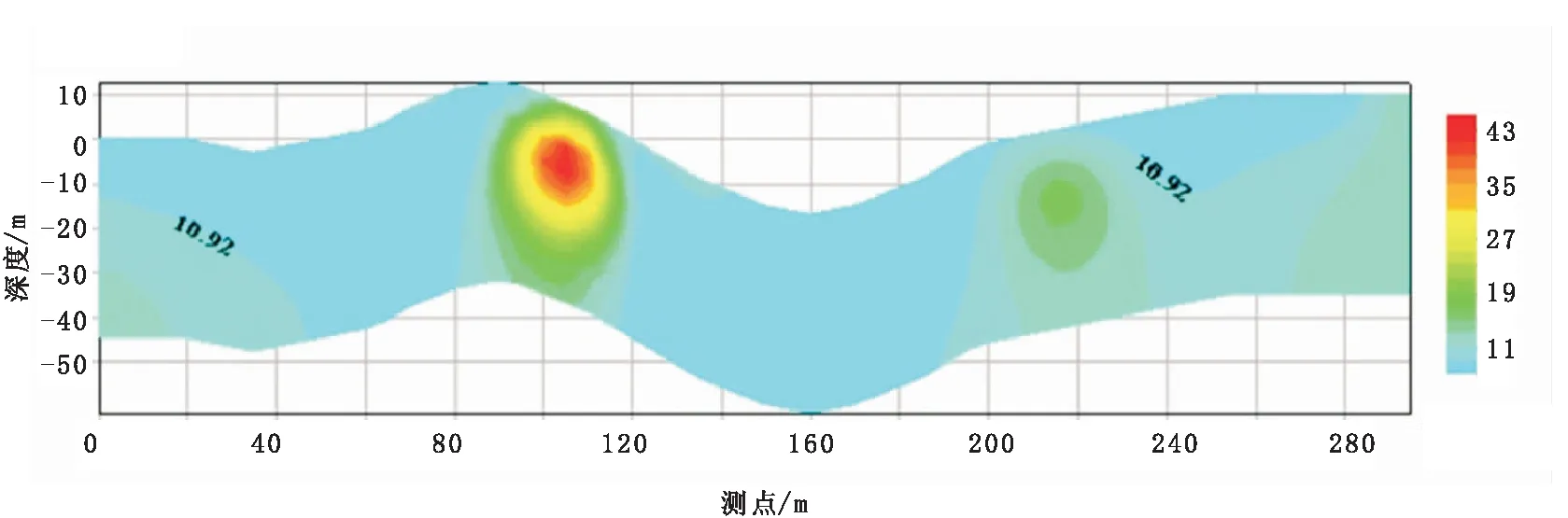
图9 反演极化率断面图Fig.9 IP section of inversion model
在工作区的500线上,采用轴向偶极—偶极装置,开展了频率域激电的测深测量,观测参量为视电阻率ρs和绝对相位φs。工作频率4 Hz、2 Hz、1 Hz、2 S、4 S。野外工作装置如图10所示。供电极距AB=80 m、接收极距MN=80 m,点距为40 m,隔离系数n=1~12。
采用二维反演软件对4 s时的视电阻率和视相位进行反演,反演初始模型为均匀半空间,均匀半空间的物性值分别为记录点的平均视电阻率和平均视相位。图11为迭代5次的反演结果,RMS(均方误差)为13%,从图11、图12、图13和图14可以看出,实测和正演视电阻率拟断面以及实测和正演视相位拟断面形态相似程度高。
图15为500线相位和电阻率反演断面(由蓝色渐变至红色对应低值渐变至高值)及中梯激电剖面曲线,从图15中可以看出,矿致异常在相位和电阻率反演断面有明显反映,激电反演异常位置与中梯剖面曲线激电异常位置对应一致。
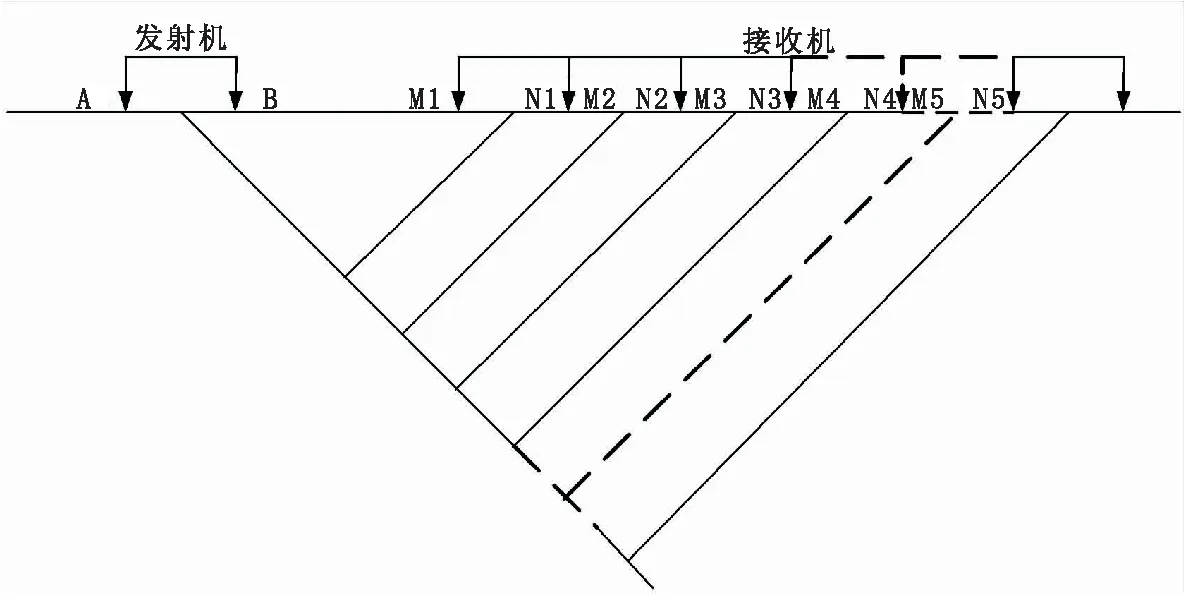
图10 相位激电轴向偶极-偶极装置示意图Fig.10 Sketch of dipole-dipole array IP

图11 实测视电阻率拟断面Fig.11 Pseudosection of observed apparent resistivity

图12 第五次迭代正演视电阻率拟断面Fig.12 Forward apparent resistivity pseudosection of the fifth iteration

图13 实测视相位拟断面Fig.13 Pseudosection of observed apparent phase

图14 第五次迭代正演视相位拟断面Fig.14 Forward apparent phase pseudosection of the fifth iteration

图15 500测线上获取的矿致异常Fig.15 Mineralization anomalies of the line 500(a)激电中梯测量剖面;(b)500 线激电深相位反演断面;(c)500 线激电深电阻率反演断面
4 结论
1)在有限元点源二维正演模拟中,采用第二类齐次边界条件结合相应的剖分技术。将二维正演模拟引入二维反演中,为偶极—偶极激电测深二维反演软件的实现奠定基础。
2)利用VC 6.0和Compaq Fortran6.6开发工具,将二维正反演算法与可视化编程技术有机集成,形成了集数据输入、数据成图、反演计算和结果多方式输出为一体的偶极—偶极激电测深二维反演软件。
3)通过理论模型合成数据和实测数据的反演表明,研制形成的二维反演软件对时间域激发极化数据和相位激电数据的反演是有效的,并能与物化探所研制的大功率多功能电法仪器配套使用。
参考文献:
[1] 阮百尧,村上裕,徐世浙. 激发极化数据的最小二乘二维反演方法[J]. 地球科学—中国地质大学学报,1999,24(6):620-623.
[2] 吴文鹂. 电法勘探工作站软件系统简介[J]. 地质与勘探,2003(增刊):147-149.
[3] 顾观文. 电法勘探工作站程序设计技术[J]. 地质与勘探,2003(增刊):152-154.
[4] 顾观文,吴文鹂,高艳芳,等. 电阻率/激电测深二维人机交互正演模拟[J]. 物探化探计算技术,2007,29:89-92.
[5] 徐世浙. 地球物理中的有限单元法[M]. 北京:科学出版社,1994.
[6] 阮百尧. 三角单元部分电导率分块连续变化点源二维电场有限元数值模拟[J].广西科学,2001,8(1):1-5.
[7] 黄俊革.三维电阻率/极化率有限元正演模拟与反演成像[D].长沙:中南大学,2003.
[8] 罗延钟,万乐,董浩斌,等.不平地形条件下高密度电阻率法的2.5维反演[J].地质与勘探,2004(增刊):172-175.
[9] 李金铭.地电场与电法勘探[M].北京:地质出版社,2005.
